12.1. 1函数 第1课时 认识函数 课件(共25张PPT) 2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 12.1. 1函数 第1课时 认识函数 课件(共25张PPT) 2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-30 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
沪科版
12.1.1 认识函数
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
学习目标
1.联系自己的学习、生活实际,通过具体情境领悟函数的概念,了解常量、变量,知道自变量与函数,能写出简单的函数表达式;
2.探究变量的发现和函数概念的形成,提高学生分析、解决问题的能力.
重点
难点
我们生活在一个变化的世界中,通常会看到在同一变化过程中,有两个相关的量,其中一个量往往随着另一个量的变化而变化.如热气球上升后到达的海拔高度随着上升时间的变化而变化……
你了解这些量之间的关系吗?
新课引入
在现实生活中,常常会需要研究两个变量之间的相互关系.例如:
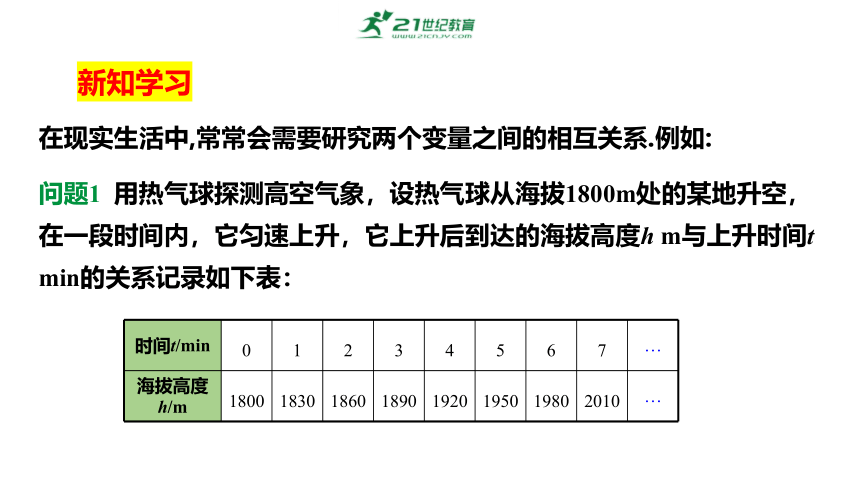
问题1 用热气球探测高空气象,设热气球从海拔1800m处的某地升空,在一段时间内,它匀速上升,它上升后到达的海拔高度h m与上升时间t min的关系记录如下表:
时间t/min 0 1 2 3 4 5 6 7 …
海拔高度h/m 1800 1830 1860 1890 1920 1950 1980 2010 …
新知学习
(1)在这个问题中,有几个量?
(2)观察上表,热气球在上升的过程中平均每分上升多少米?
(3)你能求出上升后3min、6min时热气球到达的海拔高度吗?
海拔高度h与上升时间t两个变量
30m
t=3时,h=1890;t=6时,h=1980
时间t/min 0 1 2 3 4 5 6 7 …
海拔高度h/m 1800 1830 1860 1890 1920 1950 1980 2010 …
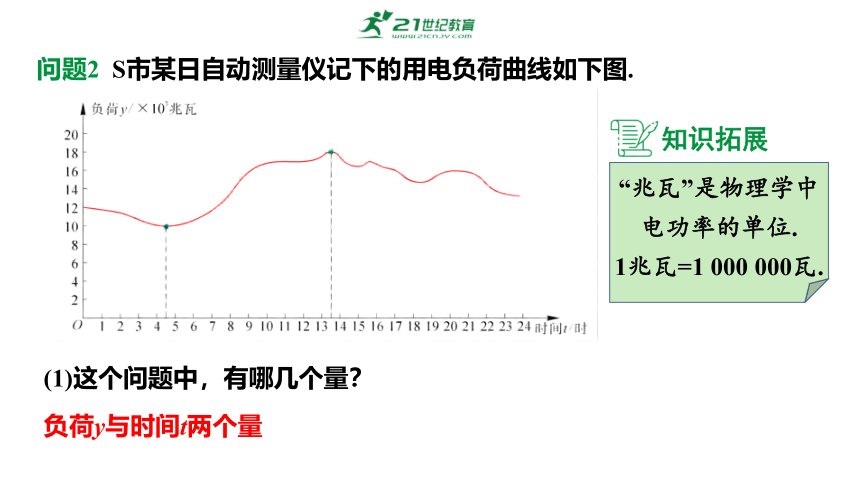
问题2 S市某日自动测量仪记下的用电负荷曲线如下图.
(1)这个问题中,有哪几个量?
负荷y与时间t两个量
“兆瓦”是物理学中电功率的单位.
1兆瓦=1 000 000瓦.
知识拓展
(2)任意给出这一天中的某一时刻,如4.5h、20h,你能找到这一时刻的用电负荷y MW(兆瓦)是多少吗?你是怎样找到的?找到的值是唯一确定的吗?
4.5h,用电负荷10(兆瓦)
20h,用电负荷16(兆瓦)
是唯一确定的.
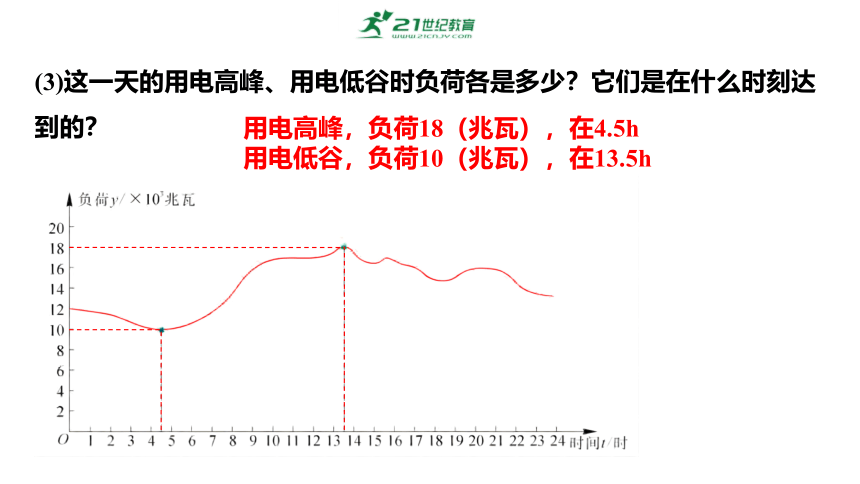
(3)这一天的用电高峰、用电低谷时负荷各是多少?它们是在什么时刻达到的?
用电高峰,负荷18(兆瓦),在4.5h
用电低谷,负荷10(兆瓦),在13.5h
问题3 汽车在行驶过程中,由于惯性的作用刹车后仍将滑行一段距离才能停住,刹车距离是分析事故原因的一个重要因素.某型号的汽车在平整路面上的刹车距离s m与车速v km/h 之间有下列经验公式:
(1)式中涉及哪几个量?
刹车距离s和车速v两个量
(2)当刹车时车速v 分别是40、80、120km/h时,相应的滑行距离s分别是多少?
当v=40时,s=6.25;当 v=80时,s=25;
当 v=120时,s=56.25.
问题1中,热气球上升高度h的数值是随时间t的数值变化而变化的,h 与t可以取不同的数值,是变量;每分上升高度为30 m,这个30在过程中保持不变,是常量.
归纳
在研究变量间关系的上述三个问题中,每个变化过程都只涉及两个变量,两个变量之间有一种对应关系,当给定其中一个变量(自变量)的值,根据此对应关系就唯一确定了另一个变量(因变量).
例如:
问题1中,t =3时,h = 1 890;t =6时,h = 1 980.
问题2中,t = 4.5时,y = 10;t = 20时,y = 16.
问题3中,v= 40时,s ≈ 6.3;v = 60时,s ≈14.1.
一般地,设在一个变化过程中有两个变量x,y,如果对于x在它允许取值范围内的每一个值,y都有唯一确定的值与它对应,那么就说x是自变量,y是x的函数.如果当x= a时,y = b,那么b叫做当自变量的值为a时的函数值.
你能指出问题1、2、3中的自变量与函数吗?
问题1中热气球上升高度h是自变量时间t的函数;
问题2中用电负荷y是自变量时间t的函数;
问题3中制动距离s是自变量车速v的函数.
例 下列关于变量x ,y 的关系式: y =2x+3; y =x2+3; y =2|x|;④ ;⑤y2-3x=10,其中表示y 是x 的函数关系的是 .
分析
y =2x+3; y =x2+3; y =2|x|;
④ ;一个x值有两个y 值与它对应
⑤y2-3x=10,一个x值有两个y 值与它对应
判断函数是否为函数关系应注意以下三点:
(1)有两个变量;
(2)一个变量的数值随着另一个变量数值的变化而变化;
(3)对于自变量的每一个确定的值,函数有且只有一个值与之对应.
方法归纳
1.甲以每小时20千米的速度行驶时,他所走过的路程s和时间t之间可用公式s=20t来表示,则下列说法正确的是( )
A.数20和s,t都是变量
B.数20和t都是变量
C.s和t都是变量
D.数20和s都是常量
C
针对训练
2.设路程为s,时间为t,速度为v,当v=60时,路程和时间的关系式为 ,这个关系式中, 是常量, 是变量,
是 的函数.
60
s=60t
t和s
s
t
3.下列关系式当中,y 不是 x 的函数的是 ( )
A. y = 2x - 3
B. y = x2 + 3
C. y = 2|x| + 3
D. y2 - 3x = 0
D
1.下列问题中,一个变量是否是另一个变量的函数?如果是,请指出自变量.
(1)改变正方形的边长 x,正方形的面积 S 随之变化;
S 是x的函数,其中x是自变量.
y 是n的函数,其中n是自变量.
(2)秀水村的耕地面积是106 m2,这个村人均占有耕地面积 y (单位:m2)随这个村人数 n 的变化而变化;
随堂练习
y 不是x的函数.
(3)P是数轴上的一个动点,它到原点的距离记为 x,它对应的实数为 y,y 随 x 的变化而变化.
2.如图是小颖0到12时的心跳速度变化图,在这一时段内心跳速度最快的时刻约为( )
A. 3时 B. 6时 C. 9时 D. 12时
C
3.甲、乙两种物质的溶解度y(g)与温度t(℃)之间的对应关系如图所示,则下列说法中,错误的是( )
A. 甲、乙两种物质的溶解度均随着温度的升高而增大
B. 当温度升高至t2℃时,甲的溶解度比乙的溶解度大
C. 当温度为0 ℃时,甲、乙的溶解度都小于20 g
D. 当温度为30 ℃时,甲、乙的溶解度相等
D
常量与变量
认识函数
在一个变化过程中,数值发生变化的量为变量,
数值始终不变的量为常量.
函数
一般地,设在一个变化过程中有两个变量x,y ,如果
对于x在它允许取值范围内的每一个值,y都有唯一
确定的值与它对应,那么就说x是自变量 ,y是x的函数.
你学会了吗?
课堂小结
沪科版
12.1.1 认识函数
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
学习目标
1.联系自己的学习、生活实际,通过具体情境领悟函数的概念,了解常量、变量,知道自变量与函数,能写出简单的函数表达式;
2.探究变量的发现和函数概念的形成,提高学生分析、解决问题的能力.
重点
难点
我们生活在一个变化的世界中,通常会看到在同一变化过程中,有两个相关的量,其中一个量往往随着另一个量的变化而变化.如热气球上升后到达的海拔高度随着上升时间的变化而变化……
你了解这些量之间的关系吗?
新课引入
在现实生活中,常常会需要研究两个变量之间的相互关系.例如:
问题1 用热气球探测高空气象,设热气球从海拔1800m处的某地升空,在一段时间内,它匀速上升,它上升后到达的海拔高度h m与上升时间t min的关系记录如下表:
时间t/min 0 1 2 3 4 5 6 7 …
海拔高度h/m 1800 1830 1860 1890 1920 1950 1980 2010 …
新知学习
(1)在这个问题中,有几个量?
(2)观察上表,热气球在上升的过程中平均每分上升多少米?
(3)你能求出上升后3min、6min时热气球到达的海拔高度吗?
海拔高度h与上升时间t两个变量
30m
t=3时,h=1890;t=6时,h=1980
时间t/min 0 1 2 3 4 5 6 7 …
海拔高度h/m 1800 1830 1860 1890 1920 1950 1980 2010 …
问题2 S市某日自动测量仪记下的用电负荷曲线如下图.
(1)这个问题中,有哪几个量?
负荷y与时间t两个量
“兆瓦”是物理学中电功率的单位.
1兆瓦=1 000 000瓦.
知识拓展
(2)任意给出这一天中的某一时刻,如4.5h、20h,你能找到这一时刻的用电负荷y MW(兆瓦)是多少吗?你是怎样找到的?找到的值是唯一确定的吗?
4.5h,用电负荷10(兆瓦)
20h,用电负荷16(兆瓦)
是唯一确定的.
(3)这一天的用电高峰、用电低谷时负荷各是多少?它们是在什么时刻达到的?
用电高峰,负荷18(兆瓦),在4.5h
用电低谷,负荷10(兆瓦),在13.5h
问题3 汽车在行驶过程中,由于惯性的作用刹车后仍将滑行一段距离才能停住,刹车距离是分析事故原因的一个重要因素.某型号的汽车在平整路面上的刹车距离s m与车速v km/h 之间有下列经验公式:
(1)式中涉及哪几个量?
刹车距离s和车速v两个量
(2)当刹车时车速v 分别是40、80、120km/h时,相应的滑行距离s分别是多少?
当v=40时,s=6.25;当 v=80时,s=25;
当 v=120时,s=56.25.
问题1中,热气球上升高度h的数值是随时间t的数值变化而变化的,h 与t可以取不同的数值,是变量;每分上升高度为30 m,这个30在过程中保持不变,是常量.
归纳
在研究变量间关系的上述三个问题中,每个变化过程都只涉及两个变量,两个变量之间有一种对应关系,当给定其中一个变量(自变量)的值,根据此对应关系就唯一确定了另一个变量(因变量).
例如:
问题1中,t =3时,h = 1 890;t =6时,h = 1 980.
问题2中,t = 4.5时,y = 10;t = 20时,y = 16.
问题3中,v= 40时,s ≈ 6.3;v = 60时,s ≈14.1.
一般地,设在一个变化过程中有两个变量x,y,如果对于x在它允许取值范围内的每一个值,y都有唯一确定的值与它对应,那么就说x是自变量,y是x的函数.如果当x= a时,y = b,那么b叫做当自变量的值为a时的函数值.
你能指出问题1、2、3中的自变量与函数吗?
问题1中热气球上升高度h是自变量时间t的函数;
问题2中用电负荷y是自变量时间t的函数;
问题3中制动距离s是自变量车速v的函数.
例 下列关于变量x ,y 的关系式: y =2x+3; y =x2+3; y =2|x|;④ ;⑤y2-3x=10,其中表示y 是x 的函数关系的是 .
分析
y =2x+3; y =x2+3; y =2|x|;
④ ;一个x值有两个y 值与它对应
⑤y2-3x=10,一个x值有两个y 值与它对应
判断函数是否为函数关系应注意以下三点:
(1)有两个变量;
(2)一个变量的数值随着另一个变量数值的变化而变化;
(3)对于自变量的每一个确定的值,函数有且只有一个值与之对应.
方法归纳
1.甲以每小时20千米的速度行驶时,他所走过的路程s和时间t之间可用公式s=20t来表示,则下列说法正确的是( )
A.数20和s,t都是变量
B.数20和t都是变量
C.s和t都是变量
D.数20和s都是常量
C
针对训练
2.设路程为s,时间为t,速度为v,当v=60时,路程和时间的关系式为 ,这个关系式中, 是常量, 是变量,
是 的函数.
60
s=60t
t和s
s
t
3.下列关系式当中,y 不是 x 的函数的是 ( )
A. y = 2x - 3
B. y = x2 + 3
C. y = 2|x| + 3
D. y2 - 3x = 0
D
1.下列问题中,一个变量是否是另一个变量的函数?如果是,请指出自变量.
(1)改变正方形的边长 x,正方形的面积 S 随之变化;
S 是x的函数,其中x是自变量.
y 是n的函数,其中n是自变量.
(2)秀水村的耕地面积是106 m2,这个村人均占有耕地面积 y (单位:m2)随这个村人数 n 的变化而变化;
随堂练习
y 不是x的函数.
(3)P是数轴上的一个动点,它到原点的距离记为 x,它对应的实数为 y,y 随 x 的变化而变化.
2.如图是小颖0到12时的心跳速度变化图,在这一时段内心跳速度最快的时刻约为( )
A. 3时 B. 6时 C. 9时 D. 12时
C
3.甲、乙两种物质的溶解度y(g)与温度t(℃)之间的对应关系如图所示,则下列说法中,错误的是( )
A. 甲、乙两种物质的溶解度均随着温度的升高而增大
B. 当温度升高至t2℃时,甲的溶解度比乙的溶解度大
C. 当温度为0 ℃时,甲、乙的溶解度都小于20 g
D. 当温度为30 ℃时,甲、乙的溶解度相等
D
常量与变量
认识函数
在一个变化过程中,数值发生变化的量为变量,
数值始终不变的量为常量.
函数
一般地,设在一个变化过程中有两个变量x,y ,如果
对于x在它允许取值范围内的每一个值,y都有唯一
确定的值与它对应,那么就说x是自变量 ,y是x的函数.
你学会了吗?
课堂小结
