12.2.6 一次函数 第6课时 一次函数解决双函数应用问题 课件(共22张PPT) 2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 12.2.6 一次函数 第6课时 一次函数解决双函数应用问题 课件(共22张PPT) 2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-30 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
沪科版
12.2.6 一次函数
解决双函数问题
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 深入了解一次函数的应用价值;
2. 能将一个具体的实际问题转化为数学问题,利用数学模型解决实际问题;
3. 从问题的解决与探究中进一步感悟函数的应用价值,培养解决实际问题的数学能力.
难点
重点
学习目标
重点
龟兔赛跑
新课引入
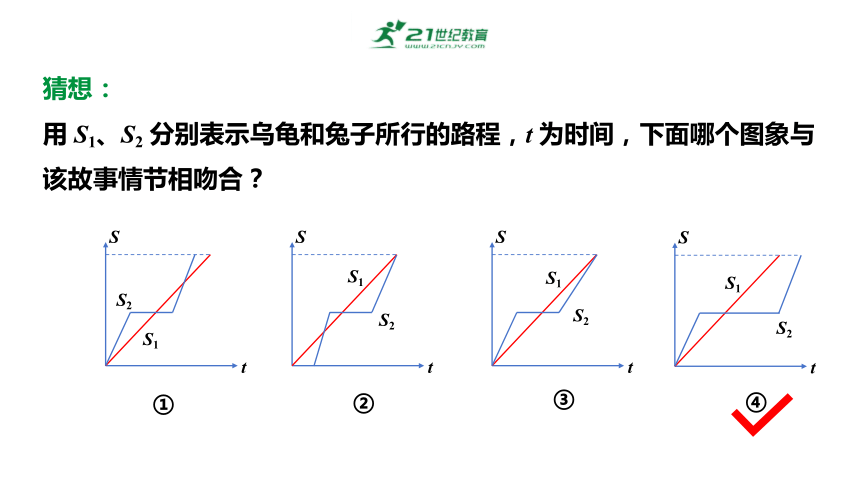
猜想:
用 S1、S2 分别表示乌龟和兔子所行的路程,t 为时间,下面哪个图象与该故事情节相吻合?
S1
S2
t
S
S1
S2
t
S
S1
S2
t
S
S1
S2
t
S
①
②
③
④
例 某单位有职工几十人,想在节假日期间组织到H地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到H地旅游的价格都是每人100元,经联系协商,甲旅行社表示可给予每位游客八折优惠;
乙旅行社表示单位先交1000元后,给予每位游客六折优惠,问该单位选择哪家旅行社,使其支付的旅游总费用较少?
新知学习
x
100x 0.8
1000+100x 0.6
比较100x 0.8和1000+100x 0.6的大小
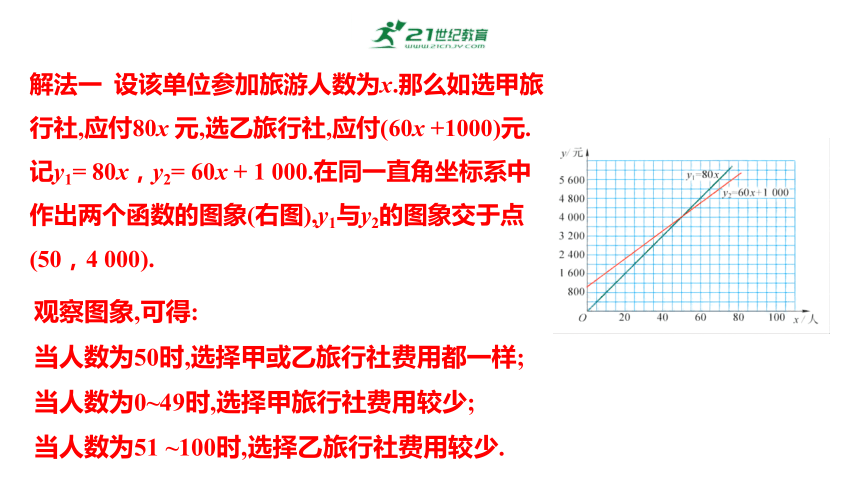
解法一 设该单位参加旅游人数为x.那么如选甲旅行社,应付80x 元,选乙旅行社,应付(60x +1000)元.
记y1= 80x,y2= 60x + 1 000.在同一直角坐标系中作出两个函数的图象(右图),y1与y2的图象交于点
(50,4 000).
观察图象,可得:
当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49时,选择甲旅行社费用较少;
当人数为51 ~100时,选择乙旅行社费用较少.
解法二 设选择甲、乙旅行社所需费用之差为y,
则y =y1- y2= 80x -(60x + 1000) = 20x - 1000.画一次函数y = 20x - 1000的图象,如图,它与x轴交点为(50, 0).由图可知:
(1)当x =50时,y =0,即y1= y2,甲、乙两家旅行社的费用一样;
(2)当x >50时,y >0,即y1> y2 ,乙旅行社的费用较低;
(3)当x <50时,y<0,即 y1归纳
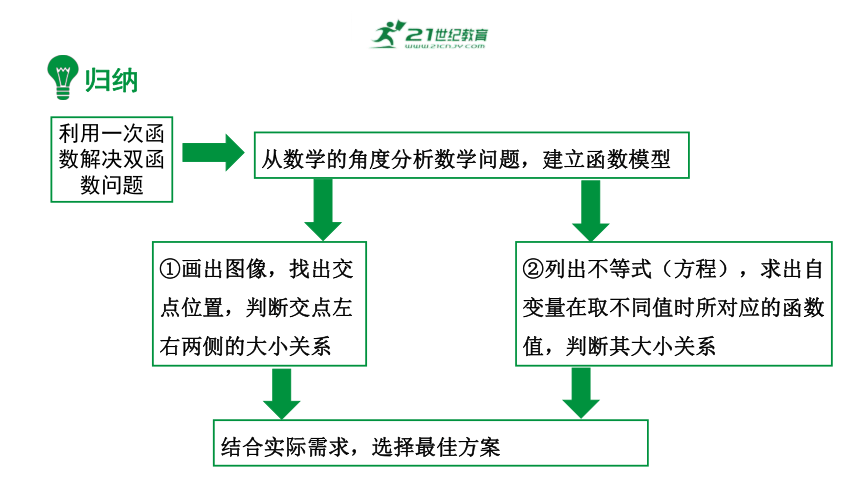
利用一次函数解决双函数问题
②列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
从数学的角度分析数学问题,建立函数模型
结合实际需求,选择最佳方案
①画出图像,找出交点位置,判断交点左右两侧的大小关系
例2 如图,l1 反映了某公司产品的销售收入与销售量的关系,l2 反映了该公司产品的销售成本与销售量的关系,根据图象填空:
(1) 当销售量为 2t 时,销售收入 = _____ 元,销售成本 = _____元;
2000
3000
(2) 当销售量为 6t 时,销售收入 = _____ 元,销售成本 = _____元;
6000
5000
(3) 当销售量为 _____ 时,销售收入等于销售成本;
4t
(4) 当销售量 ________ 时,该公司盈利 ( 收入大于成本 );当销售量 _______ 时,该公司亏损 ( 收入小于成本 );
大于 4t
小于 4t
(5) l1 对应的函数表达式是 __________ ,l2 对应的函数表达式是 _______________.
y1 = 1000x
y2 = 500x + 2000
1. 某单位准备和甲、乙两个出租车公司中的一家签订合同,设汽车每月行驶 x km,每月应付给甲公司费用为 y1 元,付给乙公司费用为 y2 元,y1,y2 与 x 的关系如图所示,该单位每月行驶的路程为 4000 km,为使费用最少则应选择 ( )
x/km
y/元
O
1000
2000
3000
甲
乙
A. 甲公司
B. 乙公司
C. 甲、乙公司都一样
D. 无法确定
B
随堂练习
2. 如图是甲、乙两家商店销售同一种产品的销售价格 y (元) 与销售量 x (件) 之间的函数图象. 下列说法:① 售2件时,甲、乙两家售价一样;②买 1 件时买乙家划算;③买三件时买甲家划算;④买乙家的 1 件售价约为 3 元,其中正确的说法是 ( ).
x/件
y/元
O
2
4
2
甲
乙
A. ① ②
B. ② ③ ④
C. ② ③
D. ① ② ③
D
3.甲、乙两地相距40 km,小明8:00 点骑自行车由甲地去乙地,平均车速为8 km/h;小红10:00坐公共汽车也由甲地去乙地,平均车速为40 km/h.设小明所用的时间为x(h),小明与甲地的距离为y1(km),小红离甲地的距离为y2(km).
(1)分别写出y1 ,y2与x之间的函数表达式;
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
解 小明所用时间为x h, 由“路程=速度×时间” 可知y1 = 8x,自变量x 的取值范围是0≤x≤5.
由于小红比小明晚出发2 h,因此小红所用时间为(x - 2)h. 从而 y2 = 40(x - 2),自变量x 的取值范围是2≤x≤3.
(1)分别写出y1 ,y2与x之间的函数表达式;
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
过点M(0,40)作射线l 与x 轴平行,它先与射线 y2 = 40(x - 2)相交,这表明小红先到达乙地.
解 将以上两个函数的图象画在同一个直角坐标系中,如图所示.
4.今年A地将采摘200吨苹果,B地将采摘300吨.若要将这些苹果运到甲、乙两个冷藏仓库,已知甲仓库可储存240吨,乙仓库可储存260吨,从A地运往甲、乙两处的费用分别为每吨20元和25元,从B地运往甲、乙两处的费用分别为每吨15元和18元.设从A地运往甲仓库的苹果为x吨,A、B两地运往两仓库的苹果运输费用分别为yA元和yB元.
(1)分别求出yA、yB与x之间的函数关系式;
解:(1)yA=20x+25(200-x)=-5x+5000,
yB=15(240-x)+18(60+x)=3x+4680;
(2)A、B两地中,哪个的运费较少?
(2)解:∵yA-yB=(-5x+5000)-(3x+4680)=-8x+320,
∴当-8x+320>0,即x<40时,B地的运费较少;
当-8x+320=0,即x=40时,两地的运费一样多;
当-8x+320<0,即x>40时,A地的运费较少.
课堂小结
利用一次函数解决双函数问题
②列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
从数学的角度分析数学问题,建立函数模型
结合实际需求,选择最佳方案
①画出图像,找出交点位置,判断交点左右两侧的大小关系
沪科版
12.2.6 一次函数
解决双函数问题
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 深入了解一次函数的应用价值;
2. 能将一个具体的实际问题转化为数学问题,利用数学模型解决实际问题;
3. 从问题的解决与探究中进一步感悟函数的应用价值,培养解决实际问题的数学能力.
难点
重点
学习目标
重点
龟兔赛跑
新课引入
猜想:
用 S1、S2 分别表示乌龟和兔子所行的路程,t 为时间,下面哪个图象与该故事情节相吻合?
S1
S2
t
S
S1
S2
t
S
S1
S2
t
S
S1
S2
t
S
①
②
③
④
例 某单位有职工几十人,想在节假日期间组织到H地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到H地旅游的价格都是每人100元,经联系协商,甲旅行社表示可给予每位游客八折优惠;
乙旅行社表示单位先交1000元后,给予每位游客六折优惠,问该单位选择哪家旅行社,使其支付的旅游总费用较少?
新知学习
x
100x 0.8
1000+100x 0.6
比较100x 0.8和1000+100x 0.6的大小
解法一 设该单位参加旅游人数为x.那么如选甲旅行社,应付80x 元,选乙旅行社,应付(60x +1000)元.
记y1= 80x,y2= 60x + 1 000.在同一直角坐标系中作出两个函数的图象(右图),y1与y2的图象交于点
(50,4 000).
观察图象,可得:
当人数为50时,选择甲或乙旅行社费用都一样;
当人数为0~49时,选择甲旅行社费用较少;
当人数为51 ~100时,选择乙旅行社费用较少.
解法二 设选择甲、乙旅行社所需费用之差为y,
则y =y1- y2= 80x -(60x + 1000) = 20x - 1000.画一次函数y = 20x - 1000的图象,如图,它与x轴交点为(50, 0).由图可知:
(1)当x =50时,y =0,即y1= y2,甲、乙两家旅行社的费用一样;
(2)当x >50时,y >0,即y1> y2 ,乙旅行社的费用较低;
(3)当x <50时,y<0,即 y1
利用一次函数解决双函数问题
②列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
从数学的角度分析数学问题,建立函数模型
结合实际需求,选择最佳方案
①画出图像,找出交点位置,判断交点左右两侧的大小关系
例2 如图,l1 反映了某公司产品的销售收入与销售量的关系,l2 反映了该公司产品的销售成本与销售量的关系,根据图象填空:
(1) 当销售量为 2t 时,销售收入 = _____ 元,销售成本 = _____元;
2000
3000
(2) 当销售量为 6t 时,销售收入 = _____ 元,销售成本 = _____元;
6000
5000
(3) 当销售量为 _____ 时,销售收入等于销售成本;
4t
(4) 当销售量 ________ 时,该公司盈利 ( 收入大于成本 );当销售量 _______ 时,该公司亏损 ( 收入小于成本 );
大于 4t
小于 4t
(5) l1 对应的函数表达式是 __________ ,l2 对应的函数表达式是 _______________.
y1 = 1000x
y2 = 500x + 2000
1. 某单位准备和甲、乙两个出租车公司中的一家签订合同,设汽车每月行驶 x km,每月应付给甲公司费用为 y1 元,付给乙公司费用为 y2 元,y1,y2 与 x 的关系如图所示,该单位每月行驶的路程为 4000 km,为使费用最少则应选择 ( )
x/km
y/元
O
1000
2000
3000
甲
乙
A. 甲公司
B. 乙公司
C. 甲、乙公司都一样
D. 无法确定
B
随堂练习
2. 如图是甲、乙两家商店销售同一种产品的销售价格 y (元) 与销售量 x (件) 之间的函数图象. 下列说法:① 售2件时,甲、乙两家售价一样;②买 1 件时买乙家划算;③买三件时买甲家划算;④买乙家的 1 件售价约为 3 元,其中正确的说法是 ( ).
x/件
y/元
O
2
4
2
甲
乙
A. ① ②
B. ② ③ ④
C. ② ③
D. ① ② ③
D
3.甲、乙两地相距40 km,小明8:00 点骑自行车由甲地去乙地,平均车速为8 km/h;小红10:00坐公共汽车也由甲地去乙地,平均车速为40 km/h.设小明所用的时间为x(h),小明与甲地的距离为y1(km),小红离甲地的距离为y2(km).
(1)分别写出y1 ,y2与x之间的函数表达式;
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
解 小明所用时间为x h, 由“路程=速度×时间” 可知y1 = 8x,自变量x 的取值范围是0≤x≤5.
由于小红比小明晚出发2 h,因此小红所用时间为(x - 2)h. 从而 y2 = 40(x - 2),自变量x 的取值范围是2≤x≤3.
(1)分别写出y1 ,y2与x之间的函数表达式;
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
过点M(0,40)作射线l 与x 轴平行,它先与射线 y2 = 40(x - 2)相交,这表明小红先到达乙地.
解 将以上两个函数的图象画在同一个直角坐标系中,如图所示.
4.今年A地将采摘200吨苹果,B地将采摘300吨.若要将这些苹果运到甲、乙两个冷藏仓库,已知甲仓库可储存240吨,乙仓库可储存260吨,从A地运往甲、乙两处的费用分别为每吨20元和25元,从B地运往甲、乙两处的费用分别为每吨15元和18元.设从A地运往甲仓库的苹果为x吨,A、B两地运往两仓库的苹果运输费用分别为yA元和yB元.
(1)分别求出yA、yB与x之间的函数关系式;
解:(1)yA=20x+25(200-x)=-5x+5000,
yB=15(240-x)+18(60+x)=3x+4680;
(2)A、B两地中,哪个的运费较少?
(2)解:∵yA-yB=(-5x+5000)-(3x+4680)=-8x+320,
∴当-8x+320>0,即x<40时,B地的运费较少;
当-8x+320=0,即x=40时,两地的运费一样多;
当-8x+320<0,即x>40时,A地的运费较少.
课堂小结
利用一次函数解决双函数问题
②列出不等式(方程),求出自变量在取不同值时所对应的函数值,判断其大小关系
从数学的角度分析数学问题,建立函数模型
结合实际需求,选择最佳方案
①画出图像,找出交点位置,判断交点左右两侧的大小关系
