22.3一元二次方程实践与探索课件
图片预览






文档简介
课件23张PPT。一元二次方程实践与探索某林场计划修一条长750m,断面为等腰梯形的渠道,断面面积为1.6m2,上口宽比渠深多2m,渠底比渠深多0.4m.
(1)渠道的上口宽与渠底宽各是多少?
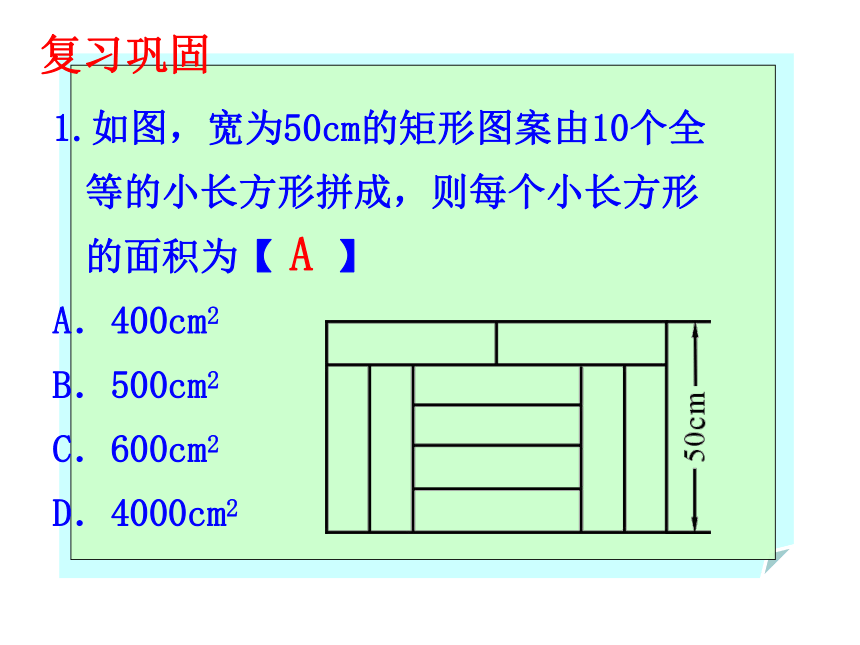
(2)如果计划每天挖土48m3,需要多少天才能把这条渠道挖完?分析:因为渠深最小,为了便于计算,不妨设渠深为xm,则上口宽为(x+2)m,渠底为(x+0.4)m,那么,根据梯形的面积公式便可建模.复习巩固解:(1)设渠深为xm 则渠底为(x+0.4)m,上口宽为(x+2)m依题意,得:整理,得:5x2+6x-8=0 解得:x1=0.8m,x2=-2(不合题意,舍去)∴上口宽为2.8m,渠底为1.2m.答:渠道的上口宽与渠底深各是2.8m和1.2m;需要25天才能挖完渠道.1.如图,宽为50cm的矩形图案由10个全等的小长方形拼成,则每个小长方形的面积为【 】
A.400cm2
B.500cm2
C.600cm2
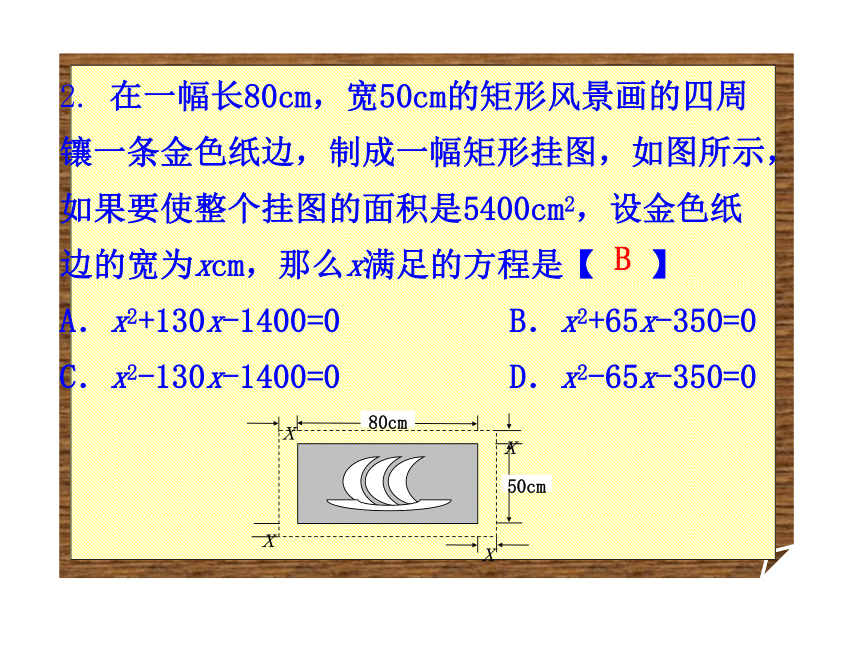
D.4000cm2A复习巩固2. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是【 】
A.x2+130x-1400=0 B.x2+65x-350=0
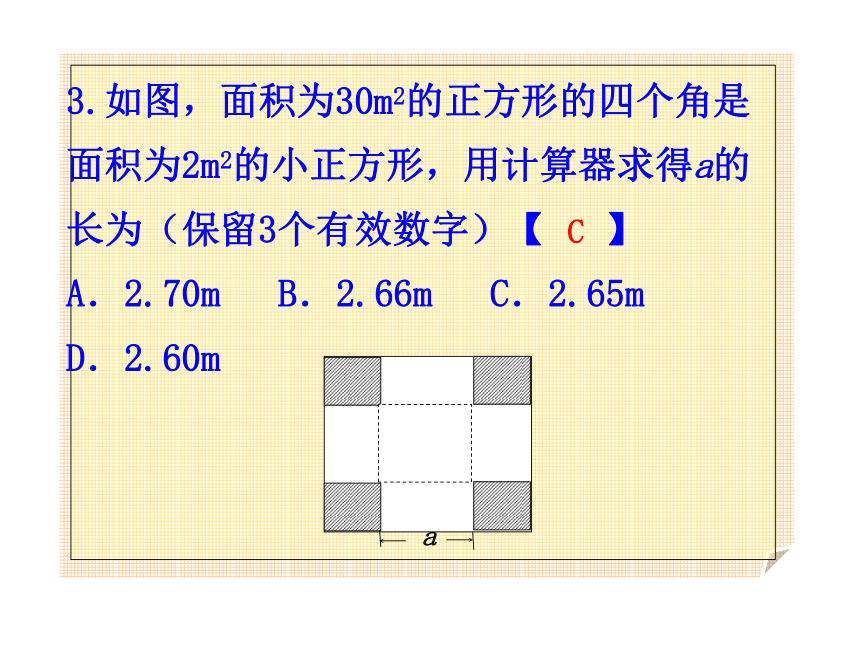
C.x2-130x-1400=0 D.x2-65x-350=0B3.如图,面积为30m2的正方形的四个角是面积为2m2的小正方形,用计算器求得a的长为(保留3个有效数字)【 】
A.2.70m B.2.66m C.2.65m D.2.60mC练习:4.如图,是长方形鸡场平面示意图,一边靠墙,另外三面用竹篱笆围成,若竹篱笆总长为35m,所围的面积为150m2,则此长方形鸡场的长、宽分别为_______.练习:5、围绕长方形公园的栅栏长280m.已知该公园的面积为4800m2.求这个公园的长与宽. 增长率类型应用题 有一个人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个? 开始有一人患了流感,第一轮的传染源就是这个
人,他传染了x个人,用代数式表示,第一轮后共有
_______人患了流感; 第二轮传染中,这些人中的每个人又传染了x个
人,用代数式示,第二轮后公有________人患了流感.分析:设每轮传染中平均一个人传染了x个人.列方程1+x+x(1+x)=121解方程,得x1=_____, x2=____. 平均一个人传染了____个人.10-1210如果按照这样的传染速度,三轮传染后有多少人患流感?平均每人传染10人,第二轮传染的人数是110人,第三轮为10×110=1100,三轮共传染了1+10+110+1100=1221人三轮传染的总人数为:( 1+x ) + x( 1+x ) + x·x( 1+x )=(1+10)+10(1+10)+10×10(1+10)= 11+110+1100=1221两年前生产1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?分析:
容易求出,甲种药品成本的年平均下降额为:
乙种药品成本的年平均下降额为:
显然,乙种药品成本的年平均下降额较大.但是年平均下降额(元)不等同于年平均下降率(百分数).(5000-3000)÷2=1000(元)(6000-3600)÷2=1200(元)解:设甲种药品成本的年平均下降率为x,则一年后甲种药品成本为5000(1-x)元,两年后甲种药品成本为5000(1-x)2元,于是有5000(1-x)2=3000解方程,得:x1≈0.225,x2≈1.775根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%6000 ( 1-y )2 = 3600解:设乙种药品的下降率为y列方程解方程,得y1≈0.225,y2≈-1.775根据问题的实际意义,乙种药品成本的年平均下降率约为22.5%。甲乙两种药品成本的平均下降率相同,都是22.5%乙种药品成本的年平均下降率是多少?请比较两种药品成本的年平均下降率.经过计算,你能得出什么结论?成本下降额较大的药品,它的成本下降率一定也较大吗?应怎样全面地比较几个对象的变化状况?得到的结论就是:甲乙两种药品的平均下降率相同成本下降额较大的药品,它的成本下降率不一定较大.不但要考虑它们的平均下降额,而且要考虑它们的平均下降率. 1、某钢铁厂去年1月某种钢产量为5000吨,3月上升到7200吨,这两个月平均每月增长的百分率是多少? 做 一 做 2、某种药品,原来每盒售价96元,由于两次降价;现在每盒售价54元。平均每次降价百分之几?解:设平均每月增长的百分率为x,依题意,得
解这个方程,得 因为不合题意,所以只能取答:平均每月增长的百分率是问题解答如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头:小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航,一般补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
(1)小岛D和小岛F相距多少海里?
(2)已知军舰的速度是补给船的2倍,
军舰在由B到C的途中与补给船相遇于E
处,那么相遇时补给船航行了多少海
里?(结果精确到0.1海里)分析:(1)因为依题意可知△ABC是等腰直角三角形,△DFC也是等腰直角三角形,AC可求,CD就可求,因此由勾股定理便可求DF的长.(2)要求补给船航行的距离就是求DE的长度,DF已求,因此,只要在Rt△DEF中,由勾股定理即可求.列一元二次方程解应用题的步骤与列一元一次方程解应用
题的步骤类似,即审、设、列、解、检、答.这里要特别注意:在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求. 小结
(1)渠道的上口宽与渠底宽各是多少?
(2)如果计划每天挖土48m3,需要多少天才能把这条渠道挖完?分析:因为渠深最小,为了便于计算,不妨设渠深为xm,则上口宽为(x+2)m,渠底为(x+0.4)m,那么,根据梯形的面积公式便可建模.复习巩固解:(1)设渠深为xm 则渠底为(x+0.4)m,上口宽为(x+2)m依题意,得:整理,得:5x2+6x-8=0 解得:x1=0.8m,x2=-2(不合题意,舍去)∴上口宽为2.8m,渠底为1.2m.答:渠道的上口宽与渠底深各是2.8m和1.2m;需要25天才能挖完渠道.1.如图,宽为50cm的矩形图案由10个全等的小长方形拼成,则每个小长方形的面积为【 】
A.400cm2
B.500cm2
C.600cm2
D.4000cm2A复习巩固2. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是【 】
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0B3.如图,面积为30m2的正方形的四个角是面积为2m2的小正方形,用计算器求得a的长为(保留3个有效数字)【 】
A.2.70m B.2.66m C.2.65m D.2.60mC练习:4.如图,是长方形鸡场平面示意图,一边靠墙,另外三面用竹篱笆围成,若竹篱笆总长为35m,所围的面积为150m2,则此长方形鸡场的长、宽分别为_______.练习:5、围绕长方形公园的栅栏长280m.已知该公园的面积为4800m2.求这个公园的长与宽. 增长率类型应用题 有一个人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个? 开始有一人患了流感,第一轮的传染源就是这个
人,他传染了x个人,用代数式表示,第一轮后共有
_______人患了流感; 第二轮传染中,这些人中的每个人又传染了x个
人,用代数式示,第二轮后公有________人患了流感.分析:设每轮传染中平均一个人传染了x个人.列方程1+x+x(1+x)=121解方程,得x1=_____, x2=____. 平均一个人传染了____个人.10-1210如果按照这样的传染速度,三轮传染后有多少人患流感?平均每人传染10人,第二轮传染的人数是110人,第三轮为10×110=1100,三轮共传染了1+10+110+1100=1221人三轮传染的总人数为:( 1+x ) + x( 1+x ) + x·x( 1+x )=(1+10)+10(1+10)+10×10(1+10)= 11+110+1100=1221两年前生产1吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?分析:
容易求出,甲种药品成本的年平均下降额为:
乙种药品成本的年平均下降额为:
显然,乙种药品成本的年平均下降额较大.但是年平均下降额(元)不等同于年平均下降率(百分数).(5000-3000)÷2=1000(元)(6000-3600)÷2=1200(元)解:设甲种药品成本的年平均下降率为x,则一年后甲种药品成本为5000(1-x)元,两年后甲种药品成本为5000(1-x)2元,于是有5000(1-x)2=3000解方程,得:x1≈0.225,x2≈1.775根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%6000 ( 1-y )2 = 3600解:设乙种药品的下降率为y列方程解方程,得y1≈0.225,y2≈-1.775根据问题的实际意义,乙种药品成本的年平均下降率约为22.5%。甲乙两种药品成本的平均下降率相同,都是22.5%乙种药品成本的年平均下降率是多少?请比较两种药品成本的年平均下降率.经过计算,你能得出什么结论?成本下降额较大的药品,它的成本下降率一定也较大吗?应怎样全面地比较几个对象的变化状况?得到的结论就是:甲乙两种药品的平均下降率相同成本下降额较大的药品,它的成本下降率不一定较大.不但要考虑它们的平均下降额,而且要考虑它们的平均下降率. 1、某钢铁厂去年1月某种钢产量为5000吨,3月上升到7200吨,这两个月平均每月增长的百分率是多少? 做 一 做 2、某种药品,原来每盒售价96元,由于两次降价;现在每盒售价54元。平均每次降价百分之几?解:设平均每月增长的百分率为x,依题意,得
解这个方程,得 因为不合题意,所以只能取答:平均每月增长的百分率是问题解答如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头:小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航,一般补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
(1)小岛D和小岛F相距多少海里?
(2)已知军舰的速度是补给船的2倍,
军舰在由B到C的途中与补给船相遇于E
处,那么相遇时补给船航行了多少海
里?(结果精确到0.1海里)分析:(1)因为依题意可知△ABC是等腰直角三角形,△DFC也是等腰直角三角形,AC可求,CD就可求,因此由勾股定理便可求DF的长.(2)要求补给船航行的距离就是求DE的长度,DF已求,因此,只要在Rt△DEF中,由勾股定理即可求.列一元二次方程解应用题的步骤与列一元一次方程解应用
题的步骤类似,即审、设、列、解、检、答.这里要特别注意:在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求. 小结
