七年级数学冀教版(2024)上册 1.5.1 有理数的加法法则 课件 (共30张PPT)
文档属性
| 名称 | 七年级数学冀教版(2024)上册 1.5.1 有理数的加法法则 课件 (共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-30 21:43:34 | ||
图片预览









文档简介
(共30张PPT)
第一章 有理数
1.5 有理数的加法
(第1课时)
1.经历探究有理数加法法则的过程,体会分类讨论与数形结合的数学思想方法,培养抽象概括能力。
2.掌握有理数加法的运算法则,能运用有理数的加法运算解决简单的实际问题,体会数学与现实世界的联系,增强数学的应用意识。
学习重点:理解有理数的加法法则.
学习难点:熟练利用加法法则进行加法运算.
石家庄某天最低气温是-15°C,最高气温比最低气温高12°C,石家庄这天的最高气温是多少度呢?如何列算式呢?
-15+12=?
在操场上,小亮在一段东西走向的路上行走,规定向东为正,向西为负:
学生活动一 【探究有理数加法法则】
先向东走3步,再向东走2步,小亮两次运动的结果:向 走 步。
怎样用算式表示?
东
5
(+3)+(+2)=+5
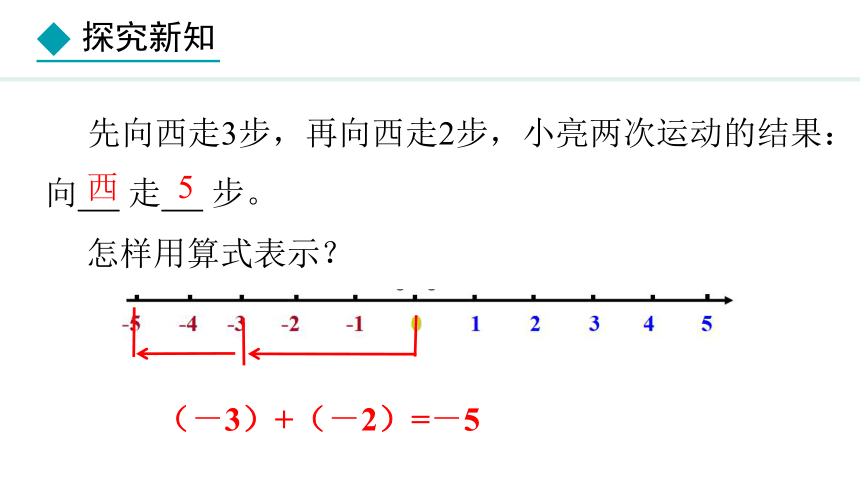
先向西走3步,再向西走2步,小亮两次运动的结果:向 走 步。
怎样用算式表示?
西
5
(-3)+(-2)=-5
先向东走3步,再向西走3步,小亮两次运动的结果:
怎样用算式表示?
原地 不动
(+3)+( -3)=0
向 走 步。
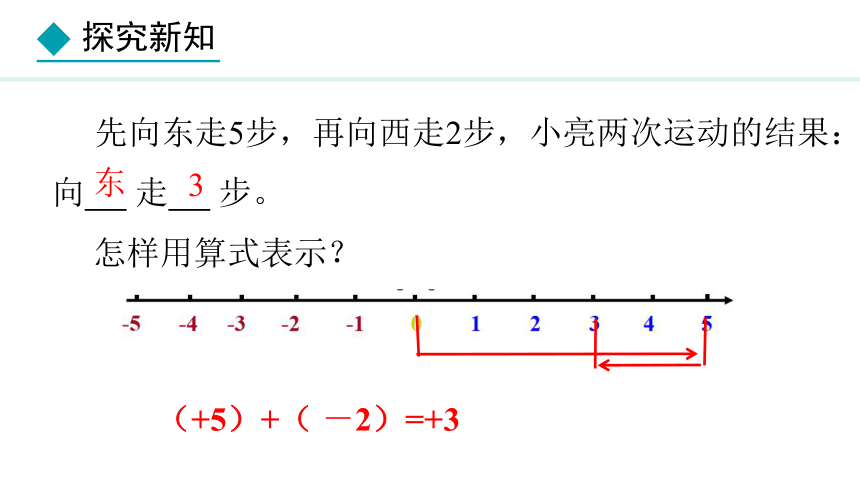
先向东走5步,再向西走2步,小亮两次运动的结果:向 走 步。
怎样用算式表示?
东
3
(+5)+( -2)=+3
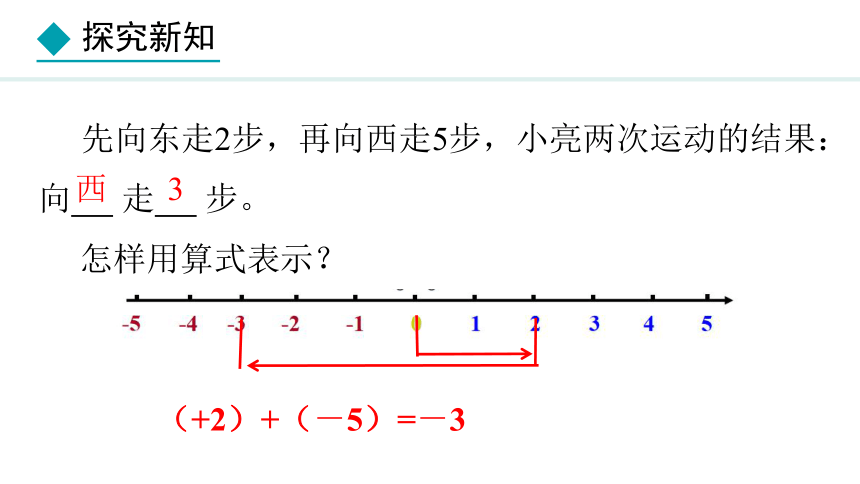
先向东走2步,再向西走5步,小亮两次运动的结果:向 走 步。
怎样用算式表示?
西
3
(+2)+(-5)=-3
先向西走5步,再向东走0步,小亮两次运动的结果:向 走 步。
怎样用算式表示?
西
5
(-5)+(0)=-5
(1)(+3)+(+2)=(+5)
(2) (-3)+(-2)=(-5)
(3)(+3)+(-3)=(0)
(4)(+5)+(-2)=(+3)
(5)(+2)+(-5)=(-3)
(6)(-5)+(0)=(-5)
观察上述算式,思考有理数的加法运算如何确定和的符号?
如何确定和的绝对值?
有理数加法法则:
同号两数相加,取相同的符号,并把绝对值相加。
异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值大的加数的符号,并用较大的绝对值减去较小的绝对值。
一个数同0相加,仍得这个数。
学生活动二 【探究有理数加法法则的应用】
例1 计算:
(1)(-8)+(-5); (2)(+2.5)+(-2.5);
(3)(-5)+0; (4)+.
解:(1)(+8)+(+5)
=+(8+5)
=+13
(2)(+2.5)+( -2.5)
=0
同号两数相加,取相同的符号,并把绝对值相加.
异号两数相加,绝对值相等时和为0.
(3)
异号两数相加,绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
同号两数相加,取相同的符号,并把绝对值相加.
(4)
例2:如图,海平面的高度为0m,一艘潜艇从海平面先下潜40m,再上升15m,求现在这艘潜艇相对于海平面的位置。(上升为正,下潜为负)
解:潜水艇下潜40m,记作-40m;上升15m,记作+15m.根据题意,得
(-40)+(+15)
=-(40 -25)=-25(m)
答:现在这艘潜艇位于海平面下25米处.
1.用“>”或“<”号填空:
(1)如果a>0,b>0,那么a+b 0;
(2)如果a<0,b<0,那么a+b 0;
(3)如果a>0,b<0,|a|>|b|,那么a+b 0;
(4)如果a<0,b>0,|a|>|b|,那么a+b 0.
>
<
>
<
2.分别根据下列条件,利用|a|与|b|表示a与b的和:
(1)a>0,b>0;
(2) a<0,b<0;
(3)a>0,b<0,|a|>|b|;
(4)a>0,b<0,|a|<|b|.
3.一只小虫从某点O出发在一条直线上爬行,规定向右爬行为正,向左爬行为负.小虫共爬行5次,小虫爬行的路程依次记为(单位:厘米):-5,-3,+10,-4,+8.
(1)小虫最后的位置在哪里?
(2)若小虫的爬行速度保持不变,共用了6分钟,则小虫的爬行速度是多少?
解:(1)(-5)+(-3)+(+10)+(-4)+(+8)
=-8+(+10)+(-4)+(+8)
=+2+(-4)+(+8)
=-2+(+8)
=6(厘米).
答:小虫最后在离出发点右侧6厘米处.
解: (2)|-5|+|-3|+|+10|+|-4|+|+8|
=5+3+10+4+8
=30(厘米),
30÷6=5(厘米/分).
答:小虫的爬行速度为5厘米/分.
本节课我们研究了有理数的加法,请同学们带着以下问题进行总结:
(1)有理数的加法法则?确定加法运算的结果要从哪两个方面考虑?
(2)在学习有理数的加法法则的过程中,你经历了什么?这个过程中用到了哪些数学方法?积累了哪些活动经验?
1.计算
(1)(-0.6)+(-2.7); (2)3.7+(-8.4);
(3)(-0.6)+3; (4)3.22+1.78;
(5)7+(-3.3); (6)(-1.9)+(-0.11);
(7)(-9.18)+6.18; (8)4.2+(-6.7).
解:
(1)-3.3;(2) -4.7; (3) 2.4;(4)5;
(5)3.7; (6)-2.01; (7)-3;(8)-2.5.
2.若 ,且 x<0 , y>0 ,则x+y=( )
A. 1 B. -1 C. 5 D. -5
B
变式:若 ,则x+y = .
3.下列运算正确的个数为( )
A.0个 B.1个 C.2个 D.3个
B
完成课后习题+练习册.
第一章 有理数
1.5 有理数的加法
(第1课时)
1.经历探究有理数加法法则的过程,体会分类讨论与数形结合的数学思想方法,培养抽象概括能力。
2.掌握有理数加法的运算法则,能运用有理数的加法运算解决简单的实际问题,体会数学与现实世界的联系,增强数学的应用意识。
学习重点:理解有理数的加法法则.
学习难点:熟练利用加法法则进行加法运算.
石家庄某天最低气温是-15°C,最高气温比最低气温高12°C,石家庄这天的最高气温是多少度呢?如何列算式呢?
-15+12=?
在操场上,小亮在一段东西走向的路上行走,规定向东为正,向西为负:
学生活动一 【探究有理数加法法则】
先向东走3步,再向东走2步,小亮两次运动的结果:向 走 步。
怎样用算式表示?
东
5
(+3)+(+2)=+5
先向西走3步,再向西走2步,小亮两次运动的结果:向 走 步。
怎样用算式表示?
西
5
(-3)+(-2)=-5
先向东走3步,再向西走3步,小亮两次运动的结果:
怎样用算式表示?
原地 不动
(+3)+( -3)=0
向 走 步。
先向东走5步,再向西走2步,小亮两次运动的结果:向 走 步。
怎样用算式表示?
东
3
(+5)+( -2)=+3
先向东走2步,再向西走5步,小亮两次运动的结果:向 走 步。
怎样用算式表示?
西
3
(+2)+(-5)=-3
先向西走5步,再向东走0步,小亮两次运动的结果:向 走 步。
怎样用算式表示?
西
5
(-5)+(0)=-5
(1)(+3)+(+2)=(+5)
(2) (-3)+(-2)=(-5)
(3)(+3)+(-3)=(0)
(4)(+5)+(-2)=(+3)
(5)(+2)+(-5)=(-3)
(6)(-5)+(0)=(-5)
观察上述算式,思考有理数的加法运算如何确定和的符号?
如何确定和的绝对值?
有理数加法法则:
同号两数相加,取相同的符号,并把绝对值相加。
异号两数相加,绝对值相等时和为0;绝对值不相等时,取绝对值大的加数的符号,并用较大的绝对值减去较小的绝对值。
一个数同0相加,仍得这个数。
学生活动二 【探究有理数加法法则的应用】
例1 计算:
(1)(-8)+(-5); (2)(+2.5)+(-2.5);
(3)(-5)+0; (4)+.
解:(1)(+8)+(+5)
=+(8+5)
=+13
(2)(+2.5)+( -2.5)
=0
同号两数相加,取相同的符号,并把绝对值相加.
异号两数相加,绝对值相等时和为0.
(3)
异号两数相加,绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.
同号两数相加,取相同的符号,并把绝对值相加.
(4)
例2:如图,海平面的高度为0m,一艘潜艇从海平面先下潜40m,再上升15m,求现在这艘潜艇相对于海平面的位置。(上升为正,下潜为负)
解:潜水艇下潜40m,记作-40m;上升15m,记作+15m.根据题意,得
(-40)+(+15)
=-(40 -25)=-25(m)
答:现在这艘潜艇位于海平面下25米处.
1.用“>”或“<”号填空:
(1)如果a>0,b>0,那么a+b 0;
(2)如果a<0,b<0,那么a+b 0;
(3)如果a>0,b<0,|a|>|b|,那么a+b 0;
(4)如果a<0,b>0,|a|>|b|,那么a+b 0.
>
<
>
<
2.分别根据下列条件,利用|a|与|b|表示a与b的和:
(1)a>0,b>0;
(2) a<0,b<0;
(3)a>0,b<0,|a|>|b|;
(4)a>0,b<0,|a|<|b|.
3.一只小虫从某点O出发在一条直线上爬行,规定向右爬行为正,向左爬行为负.小虫共爬行5次,小虫爬行的路程依次记为(单位:厘米):-5,-3,+10,-4,+8.
(1)小虫最后的位置在哪里?
(2)若小虫的爬行速度保持不变,共用了6分钟,则小虫的爬行速度是多少?
解:(1)(-5)+(-3)+(+10)+(-4)+(+8)
=-8+(+10)+(-4)+(+8)
=+2+(-4)+(+8)
=-2+(+8)
=6(厘米).
答:小虫最后在离出发点右侧6厘米处.
解: (2)|-5|+|-3|+|+10|+|-4|+|+8|
=5+3+10+4+8
=30(厘米),
30÷6=5(厘米/分).
答:小虫的爬行速度为5厘米/分.
本节课我们研究了有理数的加法,请同学们带着以下问题进行总结:
(1)有理数的加法法则?确定加法运算的结果要从哪两个方面考虑?
(2)在学习有理数的加法法则的过程中,你经历了什么?这个过程中用到了哪些数学方法?积累了哪些活动经验?
1.计算
(1)(-0.6)+(-2.7); (2)3.7+(-8.4);
(3)(-0.6)+3; (4)3.22+1.78;
(5)7+(-3.3); (6)(-1.9)+(-0.11);
(7)(-9.18)+6.18; (8)4.2+(-6.7).
解:
(1)-3.3;(2) -4.7; (3) 2.4;(4)5;
(5)3.7; (6)-2.01; (7)-3;(8)-2.5.
2.若 ,且 x<0 , y>0 ,则x+y=( )
A. 1 B. -1 C. 5 D. -5
B
变式:若 ,则x+y = .
3.下列运算正确的个数为( )
A.0个 B.1个 C.2个 D.3个
B
完成课后习题+练习册.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
