苏教版数学六年级上册4.1 解决问题的策略(一)课件(共35张PPT)
文档属性
| 名称 | 苏教版数学六年级上册4.1 解决问题的策略(一)课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-29 23:55:46 | ||
图片预览











文档简介
(共35张PPT)
苏教版小学数学六年级上册
4.1 解决问题的策略(1)
新课标 核心素养
使学生初步学会运用假设的策略分析数量关系,能根据问题的特点确定假设的思路,理解假设的解题过程,能运用假设策略解决相应的实际问题。
使学生经历用假设解决实际问题的过程,感受假设策略对于解决特定问题的价值,进一步发展分析、推理和解决数学问题的能力。
使学生进一步积累解决问题的经验,增强解决问题的策略意识;获得解决问题的成功体验,提高学会数学的信心
1.解方程。
x+3x=64 x+ x=80
1
3
解: 4x=64
x=64÷4
x=16
解: x=80
4
3
x=80÷
4
3
x=60
2.把720毫升果汁,倒入6个同样大的杯子里,正好可以倒满,平均每个杯子的容量是多少毫升?
把一个数平均分成几份,求每份是多少,用除法计算。
720÷6=120(毫升)
答:平均每个杯子的容量是120毫升。
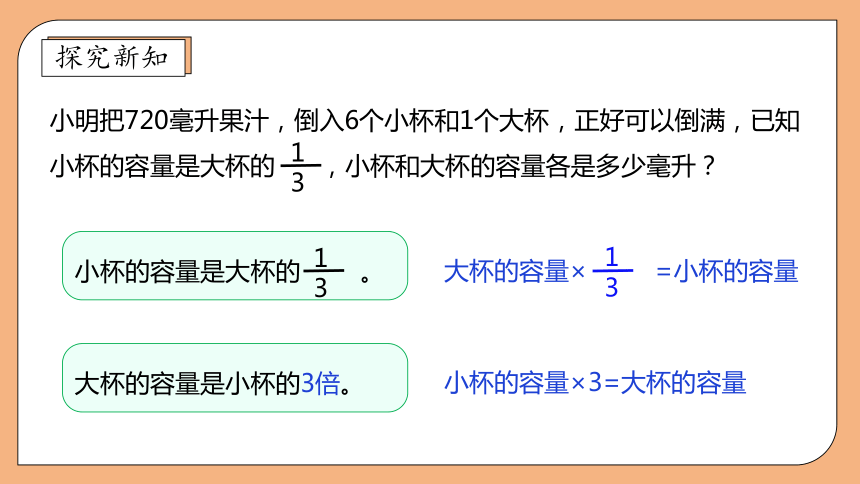
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
题中告诉了我们哪些条件?要求什么问题?
思考:
怎样理解题中数量之间的关系?与同伴交流。
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
6个小杯的容量+1个大杯的容量=720毫升
小杯的容量是大杯的 。
1
3
大杯的容量是小杯的3倍。
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
小杯的容量是大杯的 。
1
3
大杯的容量× =小杯的容量
1
3
大杯的容量是小杯的3倍。
小杯的容量×3=大杯的容量
合作提示:
在遇到比较复杂的问题时,一般会先想办法把复杂的问题转化成简单的问题。你有什么办法使这个问题变简单吗?联系刚刚找到的数量关系式想一想,再和同学说说你准备怎么解决这个问题。
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
假设把720毫升果汁全部倒入小杯。
1个大杯可以看作3个小杯。
6个小杯的容量 + =720毫升
1个大杯的容量
3个小杯的容量
9个小杯的容量=720毫升
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
画出线段图。
小杯:
大杯:
720毫升:
6小杯
1大杯
把720毫升果汁全部倒入小杯,需要(6+3)个小杯。
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
列出算式解答,并检验。
720÷(6+3)=80(毫升)
80×3=240(毫升)
检验:80×6+240=720(毫升)
答:大杯的容量是240毫升,小杯的容量是80毫升。
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
如果设小杯的容量是x毫升,你能列方程解答吗?并检验。
解:设小杯的容量是x毫升,大杯的容量就是3x毫升。
6x+3x=720
x=80
3x=80×3=240
检验: 80×6+240=720(毫升)
答:大杯的容量是240毫升,小杯的容量是80毫升。
像这样通过假设把复杂的问题转化为简单问题的方法,也是一种常用的解决问题的策略。
想一想,假设把720毫升果汁全部倒入大杯,可以倒满几个大杯?你能根据这样的假设算出结果吗?结合线段图说说。
小杯:
大杯:
720毫升:
6小杯
1大杯
3个小杯正好可以倒满1个大杯。
1大杯
1大杯
6个小杯正好可以倒满2个大杯。
如果把720毫升果汁全部倒入大杯,需要(1+2)个大杯。
选择一种方法列出算式解答,并检验。
720÷(1+2)=240(毫升)
240× =80(毫升)
1
3
检验:
80×6+240=720(毫升)
解:设大杯的容量是x毫升,小杯的容量就是 x毫升。
1
3
x+ x=720
1
3
x=240
x=240× =80
1
3
1
3
检验:80×6+240=720(毫升)
答:大杯的容量是240毫升,小杯的容量是80毫升。
回顾解决问题的过程,你有什么体会?
通过假设替换,可以转化问题,使数量关系变得简单。
假设时要弄清楚数量之间的关系。
假设时也可以用字母表示未知量,列方程解答。
在以前学习中,我们曾经运用假设的策略解决过哪些问题?
计算除法时两位数的除法,把除数当做整十数试商。
把接近整百数或整十数看作整百或整十数,来估算。
已知两个数的和与差,假设两个数同样多,分别求出这两个数。
1.看图列方程,算一算桃树和杏树各有多少棵?
杏树:
桃树:
x
200棵
x+ x=200
1
4
x=160
x=160× =40
1
4
1
4
答:桃树有40棵,杏树有160棵。
解: x=200
5
4
2.
买一套衣服需要240元,已知裤子的价钱是上衣的 ,裤子和上衣各多少元?
1
3
假设买的全是裤子,那么240元相当于(3+1)条裤子的价钱。
上衣的价钱是裤子的3倍。
240÷(3+1)=60(元)
60×3=180(元)
答:裤子60元,上衣180元。
3.饲养场的白兔比黑兔多240 只,其中黑兔的只数是白兔的 。黑兔、白兔各多少只
1
5
答:黑兔有60只,白兔有300只。
白兔的只数是黑兔的5倍,那么白兔比黑兔多(5-1)份。
240÷(5-1)=60(只)
60×5=300(只)
4.拓展练习:有两袋大米,甲袋大米的质量是乙袋的1.2倍,如果再往乙袋里装5千克大米,那么两袋大米就一样重了。原来两袋大米各多少千克?
解:设乙袋大米的重量是x千克,那么甲袋大米的重量是1.2x千克。
1.2x-x=5×2
0.2x=10
x=50
1.2x=1.2×50=60
答:甲袋大米的重量是60千克。
这节课你学会了什么?是怎么学会的?
解决问题的策略(1)
两个未知量 一个未知量
假设
复杂 简单
苏教版小学数学六年级上册
4.1 解决问题的策略(1)
新课标 核心素养
使学生初步学会运用假设的策略分析数量关系,能根据问题的特点确定假设的思路,理解假设的解题过程,能运用假设策略解决相应的实际问题。
使学生经历用假设解决实际问题的过程,感受假设策略对于解决特定问题的价值,进一步发展分析、推理和解决数学问题的能力。
使学生进一步积累解决问题的经验,增强解决问题的策略意识;获得解决问题的成功体验,提高学会数学的信心
1.解方程。
x+3x=64 x+ x=80
1
3
解: 4x=64
x=64÷4
x=16
解: x=80
4
3
x=80÷
4
3
x=60
2.把720毫升果汁,倒入6个同样大的杯子里,正好可以倒满,平均每个杯子的容量是多少毫升?
把一个数平均分成几份,求每份是多少,用除法计算。
720÷6=120(毫升)
答:平均每个杯子的容量是120毫升。
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
题中告诉了我们哪些条件?要求什么问题?
思考:
怎样理解题中数量之间的关系?与同伴交流。
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
6个小杯的容量+1个大杯的容量=720毫升
小杯的容量是大杯的 。
1
3
大杯的容量是小杯的3倍。
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
小杯的容量是大杯的 。
1
3
大杯的容量× =小杯的容量
1
3
大杯的容量是小杯的3倍。
小杯的容量×3=大杯的容量
合作提示:
在遇到比较复杂的问题时,一般会先想办法把复杂的问题转化成简单的问题。你有什么办法使这个问题变简单吗?联系刚刚找到的数量关系式想一想,再和同学说说你准备怎么解决这个问题。
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
假设把720毫升果汁全部倒入小杯。
1个大杯可以看作3个小杯。
6个小杯的容量 + =720毫升
1个大杯的容量
3个小杯的容量
9个小杯的容量=720毫升
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
画出线段图。
小杯:
大杯:
720毫升:
6小杯
1大杯
把720毫升果汁全部倒入小杯,需要(6+3)个小杯。
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
列出算式解答,并检验。
720÷(6+3)=80(毫升)
80×3=240(毫升)
检验:80×6+240=720(毫升)
答:大杯的容量是240毫升,小杯的容量是80毫升。
小明把720毫升果汁,倒入6个小杯和1个大杯,正好可以倒满,已知小杯的容量是大杯的 ,小杯和大杯的容量各是多少毫升?
1
3
如果设小杯的容量是x毫升,你能列方程解答吗?并检验。
解:设小杯的容量是x毫升,大杯的容量就是3x毫升。
6x+3x=720
x=80
3x=80×3=240
检验: 80×6+240=720(毫升)
答:大杯的容量是240毫升,小杯的容量是80毫升。
像这样通过假设把复杂的问题转化为简单问题的方法,也是一种常用的解决问题的策略。
想一想,假设把720毫升果汁全部倒入大杯,可以倒满几个大杯?你能根据这样的假设算出结果吗?结合线段图说说。
小杯:
大杯:
720毫升:
6小杯
1大杯
3个小杯正好可以倒满1个大杯。
1大杯
1大杯
6个小杯正好可以倒满2个大杯。
如果把720毫升果汁全部倒入大杯,需要(1+2)个大杯。
选择一种方法列出算式解答,并检验。
720÷(1+2)=240(毫升)
240× =80(毫升)
1
3
检验:
80×6+240=720(毫升)
解:设大杯的容量是x毫升,小杯的容量就是 x毫升。
1
3
x+ x=720
1
3
x=240
x=240× =80
1
3
1
3
检验:80×6+240=720(毫升)
答:大杯的容量是240毫升,小杯的容量是80毫升。
回顾解决问题的过程,你有什么体会?
通过假设替换,可以转化问题,使数量关系变得简单。
假设时要弄清楚数量之间的关系。
假设时也可以用字母表示未知量,列方程解答。
在以前学习中,我们曾经运用假设的策略解决过哪些问题?
计算除法时两位数的除法,把除数当做整十数试商。
把接近整百数或整十数看作整百或整十数,来估算。
已知两个数的和与差,假设两个数同样多,分别求出这两个数。
1.看图列方程,算一算桃树和杏树各有多少棵?
杏树:
桃树:
x
200棵
x+ x=200
1
4
x=160
x=160× =40
1
4
1
4
答:桃树有40棵,杏树有160棵。
解: x=200
5
4
2.
买一套衣服需要240元,已知裤子的价钱是上衣的 ,裤子和上衣各多少元?
1
3
假设买的全是裤子,那么240元相当于(3+1)条裤子的价钱。
上衣的价钱是裤子的3倍。
240÷(3+1)=60(元)
60×3=180(元)
答:裤子60元,上衣180元。
3.饲养场的白兔比黑兔多240 只,其中黑兔的只数是白兔的 。黑兔、白兔各多少只
1
5
答:黑兔有60只,白兔有300只。
白兔的只数是黑兔的5倍,那么白兔比黑兔多(5-1)份。
240÷(5-1)=60(只)
60×5=300(只)
4.拓展练习:有两袋大米,甲袋大米的质量是乙袋的1.2倍,如果再往乙袋里装5千克大米,那么两袋大米就一样重了。原来两袋大米各多少千克?
解:设乙袋大米的重量是x千克,那么甲袋大米的重量是1.2x千克。
1.2x-x=5×2
0.2x=10
x=50
1.2x=1.2×50=60
答:甲袋大米的重量是60千克。
这节课你学会了什么?是怎么学会的?
解决问题的策略(1)
两个未知量 一个未知量
假设
复杂 简单
