3.3.1抛物线及其标准方程 课件(共21张PPT)数学人教A版(2019)选择性必修 第一册
文档属性
| 名称 | 3.3.1抛物线及其标准方程 课件(共21张PPT)数学人教A版(2019)选择性必修 第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-02 08:49:45 | ||
图片预览








文档简介
(共21张PPT)
3.3.1抛物线及其标准方程
1.回顾抛物线是如何切出来的。
临界
2.如何画出抛物线呢?
第一定义?
第二定义?
我们知道,椭圆、双曲线的有共同的几何特征:
都可以看作是,在平面内与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹.
·
M
F
l
0<e <1
(2) 当e>1时,是双曲线;
(1)当0(其中定点不在定直线上)
l
F
·
M
e>1
那么,当e=1时,它又是什么曲线 ?
·
F
M
l
·
e=1
复习回顾
当e=1时,即|MF|=|MH| ,点M的轨迹是什么?
探究?
可以发现,点M随着H运动的过程中,始终有|MF|=|MH|,即点M与点F和定直线l的距离相等.点M生成的轨迹是曲线C的形状.(如图)
M
·
F
l
·
e=1
我们把这样的一条曲线叫做抛物线.
问题探究
M
·
F
l
·
e=1
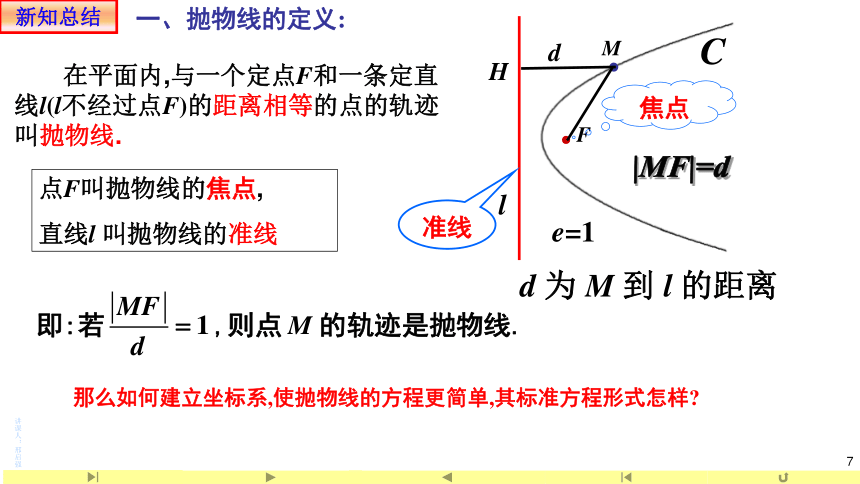
在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.
点F叫抛物线的焦点,
直线l 叫抛物线的准线
|MF|=d
d 为 M 到 l 的距离
准线
焦点
d
一、抛物线的定义:
新知总结
那么如何建立坐标系,使抛物线的方程更简单,其标准方程形式怎样
1.建:建立直角坐标系.
3. 限:根据几何条件列出等式;
4. 代:代入坐标与数据;
5. 化:化简方程.
2.设:设点(x,y);
回顾求曲线方程一般步骤:
复习回顾
6. 简:检验方程.
解法一:以l为y轴,过F点垂直于l的直线为x轴建立直角坐标系(如下图所示),则定点 设动点 ,由抛物线定义得:
化简得:
.
M(X,y)
.
x
y
O
F
l
二、标准方程的推导
学习新知
解法二:以定点F为原点,过点F垂直于l的直线为x轴建立直角坐标系(如下图所示),则定点F(0,0) ,l的方程为
设动点 ,由抛物线定义得
化简得:
二、标准方程的推导
学习新知
l
解法三:以过F且垂直于 l 的直线为x轴,垂足为K.以F,K的中点O为坐标原点建立直角坐标系xoy.
两边平方,整理得
x
K
y
o
M(x,y)
F
二、标准方程的推导
依题意得
这就是所求的轨迹方程.
学习新知
相同点:
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶点到准线的距离为p/2.
不同点:(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口方向坐标轴的正(负)方向.
记忆方法:P永为正,一次项变量为对称轴,一次项变量前系数为开口方向,且开口方向坐标轴的正(负)方向相同
新知总结
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
P的意义:抛物线的焦点到准线的距离
方程的特点:
(1)左边是二次式,
(2)右边是一次式;决定了焦点的位置.
四.四种抛物线的对比
新知总结
如何快速记住四个方程形式?
4.标准方程中p前面的正负号决定抛物线的开口方向.
1.抛物线的定义:
2.抛物线的标准方程有四种不同的形式:
每一对焦点和准线对应一种形式.
3.p的几何意义是:
焦点到准线的距离
学习小结
二次函数 的图像为什么是抛物线?
当a>0时与当a<0时,结论都为:
P66思考:
y
x
o
y=ax2
y=ax2+c
y=ax2+bx+c
深入学习
例1(1)已知抛物线的标准方程是y2 =6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程.
解:(1)因为p=3,所以焦点坐标是 , 准线方程是
,所以所求抛物线的标准方程是
(2)因为焦点在y轴的负半轴上,且
例题讲评
(3)已知抛物线的准线方程为 x = 1 ,求抛物线的标准方程
x
y
o
l
F
x = 1
解:因为准线方程是 x = 1,所以 p =2 ,且焦点在 x 轴的负半轴上,所以所求抛物线的标准方程是 y2 =-4x .
例题讲评
例1 (4)求过点A(3,2)的抛物线的标准方程
x
y
o
(3,2)
解:因为(3,2)点在第一象限,所以抛物线的开口方向只能是向右或向上,
故设抛物线的标准方程是 y2 = 2px(p>0),或 x2 = 2py(p>0),将(3,2)点的坐标分别代入上述方程可得抛物线的标准方程为
y 2 = x 或 x 2 = y
4
3
9
2
例题讲评
课堂练习
例2、点M到点F(4,0)的距离比它到直线l:x+5=0的距离小1, 求点M的轨迹方程.
x
y
o
F(4,0)
M
x+5=0
例题讲评
l
F
A
A1
x
y
B
B1
例题讲评
例3、斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长。
8
3.抛物线的标准方程类型与图象特征的对应关系及判断方法
2.抛物线的标准方程与其焦点、准线
4.注重数形结合、分类讨论思想的应用
1.抛物线的定义
小结
5.注重实际应用
3.3.1抛物线及其标准方程
1.回顾抛物线是如何切出来的。
临界
2.如何画出抛物线呢?
第一定义?
第二定义?
我们知道,椭圆、双曲线的有共同的几何特征:
都可以看作是,在平面内与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹.
·
M
F
l
0<e <1
(2) 当e>1时,是双曲线;
(1)当0
l
F
·
M
e>1
那么,当e=1时,它又是什么曲线 ?
·
F
M
l
·
e=1
复习回顾
当e=1时,即|MF|=|MH| ,点M的轨迹是什么?
探究?
可以发现,点M随着H运动的过程中,始终有|MF|=|MH|,即点M与点F和定直线l的距离相等.点M生成的轨迹是曲线C的形状.(如图)
M
·
F
l
·
e=1
我们把这样的一条曲线叫做抛物线.
问题探究
M
·
F
l
·
e=1
在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.
点F叫抛物线的焦点,
直线l 叫抛物线的准线
|MF|=d
d 为 M 到 l 的距离
准线
焦点
d
一、抛物线的定义:
新知总结
那么如何建立坐标系,使抛物线的方程更简单,其标准方程形式怎样
1.建:建立直角坐标系.
3. 限:根据几何条件列出等式;
4. 代:代入坐标与数据;
5. 化:化简方程.
2.设:设点(x,y);
回顾求曲线方程一般步骤:
复习回顾
6. 简:检验方程.
解法一:以l为y轴,过F点垂直于l的直线为x轴建立直角坐标系(如下图所示),则定点 设动点 ,由抛物线定义得:
化简得:
.
M(X,y)
.
x
y
O
F
l
二、标准方程的推导
学习新知
解法二:以定点F为原点,过点F垂直于l的直线为x轴建立直角坐标系(如下图所示),则定点F(0,0) ,l的方程为
设动点 ,由抛物线定义得
化简得:
二、标准方程的推导
学习新知
l
解法三:以过F且垂直于 l 的直线为x轴,垂足为K.以F,K的中点O为坐标原点建立直角坐标系xoy.
两边平方,整理得
x
K
y
o
M(x,y)
F
二、标准方程的推导
依题意得
这就是所求的轨迹方程.
学习新知
相同点:
(1)顶点为原点;
(2)对称轴为坐标轴;
(3)顶点到焦点的距离等于顶点到准线的距离为p/2.
不同点:(1)一次项变量为x(y),则对称轴为x(y)轴;
(2)一次项系数为正(负),则开口方向坐标轴的正(负)方向.
记忆方法:P永为正,一次项变量为对称轴,一次项变量前系数为开口方向,且开口方向坐标轴的正(负)方向相同
新知总结
y2=-2px
(p>0)
x2=2py
(p>0)
准线方程
焦点坐标
标准方程
图 形
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
x
F
O
y
l
y2=2px
(p>0)
x2=-2py
(p>0)
P的意义:抛物线的焦点到准线的距离
方程的特点:
(1)左边是二次式,
(2)右边是一次式;决定了焦点的位置.
四.四种抛物线的对比
新知总结
如何快速记住四个方程形式?
4.标准方程中p前面的正负号决定抛物线的开口方向.
1.抛物线的定义:
2.抛物线的标准方程有四种不同的形式:
每一对焦点和准线对应一种形式.
3.p的几何意义是:
焦点到准线的距离
学习小结
二次函数 的图像为什么是抛物线?
当a>0时与当a<0时,结论都为:
P66思考:
y
x
o
y=ax2
y=ax2+c
y=ax2+bx+c
深入学习
例1(1)已知抛物线的标准方程是y2 =6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程.
解:(1)因为p=3,所以焦点坐标是 , 准线方程是
,所以所求抛物线的标准方程是
(2)因为焦点在y轴的负半轴上,且
例题讲评
(3)已知抛物线的准线方程为 x = 1 ,求抛物线的标准方程
x
y
o
l
F
x = 1
解:因为准线方程是 x = 1,所以 p =2 ,且焦点在 x 轴的负半轴上,所以所求抛物线的标准方程是 y2 =-4x .
例题讲评
例1 (4)求过点A(3,2)的抛物线的标准方程
x
y
o
(3,2)
解:因为(3,2)点在第一象限,所以抛物线的开口方向只能是向右或向上,
故设抛物线的标准方程是 y2 = 2px(p>0),或 x2 = 2py(p>0),将(3,2)点的坐标分别代入上述方程可得抛物线的标准方程为
y 2 = x 或 x 2 = y
4
3
9
2
例题讲评
课堂练习
例2、点M到点F(4,0)的距离比它到直线l:x+5=0的距离小1, 求点M的轨迹方程.
x
y
o
F(4,0)
M
x+5=0
例题讲评
l
F
A
A1
x
y
B
B1
例题讲评
例3、斜率为1的直线 经过抛物线 的焦点F,且与抛物线相交于A,B两点,求线段AB的长。
8
3.抛物线的标准方程类型与图象特征的对应关系及判断方法
2.抛物线的标准方程与其焦点、准线
4.注重数形结合、分类讨论思想的应用
1.抛物线的定义
小结
5.注重实际应用
