第十三章轴对称提优测试卷(含答案) 2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 第十三章轴对称提优测试卷(含答案) 2024-2025学年人教版八年级数学上册 | 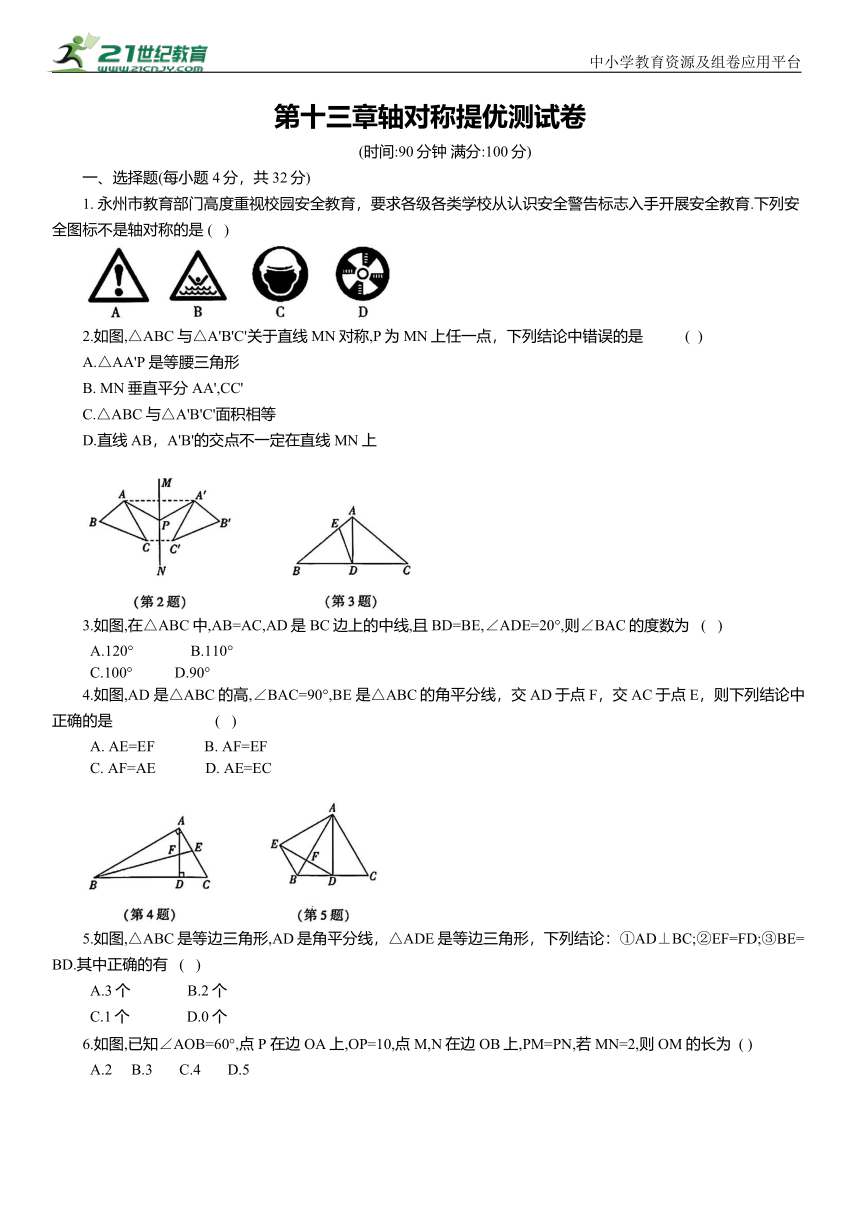 | |
| 格式 | docx | ||
| 文件大小 | 771.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 14:36:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第十三章轴对称提优测试卷
(时间:90分钟 满分:100分)
一、选择题(每小题4分,共32分)
1. 永州市教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育.下列安全图标不是轴对称的是 ( )
2.如图,△ABC与△A'B'C'关于直线MN对称,P为MN上任一点,下列结论中错误的是 ( )
A.△AA'P是等腰三角形
B. MN垂直平分AA',CC'
C.△ABC与△A'B'C'面积相等
D.直线AB,A'B'的交点不一定在直线MN上
3.如图,在△ABC中,AB=AC,AD是BC边上的中线,且BD=BE,∠ADE=20°,则∠BAC的度数为 ( )
A.120° B.110°
C.100° D.90°
4.如图,AD 是△ABC的高,∠BAC=90°,BE 是△ABC的角平分线,交AD于点F,交AC于点E,则下列结论中正确的是 ( )
A. AE=EF B. AF=EF
C. AF=AE D. AE=EC
5.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确的有 ( )
A.3个 B.2个
C.1个 D.0个
6.如图,已知∠AOB=60°,点 P 在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM的长为 ( )
A.2 B.3 C.4 D.5
7.如图,在 Rt△ABC 中,∠ACB=90°,AC=6,BC=8,AB=10,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为 ( )
A B c D.6
8.某台球桌面为如图所示的长方形ABCD,小球从A沿45°角射出,恰好经过5次碰撞到达B处,则AB∶BC等于 ( )
A.1∶2 B.2:3 C.2:5 D.3∶5
二、填空题(每小题4分,共24分)
9.在平面直角坐标系中,已知点A(m,3)与点B(4,n)关于x轴对称,那么(m+n) 的值为 .
10.小明从镜子里看到镜子对面电子钟的像为80:25:21,实际时间是 .
11.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上的A'处,折痕为CD,则∠A'DB的度数为 .
如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a,b的式子表示△ABC的周长为 .
13.如图,在△ABC 中,AB=AC,D,E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3c m,则BC的长是 cm.
14.如图,已知∠BAD=∠DAC=9°,AD⊥AE,且AB+AC=BE,则∠B= .
三、解答题(共44分)
15.(8分)在如图所示的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在网格中作出△ABC关于直线l对称的△A B C (要求A与A ,B与B ,C与C 相对应);
(2)在直线l上找一点 P,使得PA+PB 的值最小.
16.(10分)如图,在△ABC中,∠ABC=45°,CD⊥AB于点 D,AC的垂直平分线 BE 与 CD交于点 F,与AC交于点 E.
(1)判断△DBC的形状并说明理由;
(2)求证:BF=AC;
(3)试说明:
17.(12分)如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段 BC上运动(D 不与B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点 E.
(1)当∠BDA=115°时,∠BAD= °;点 D从B向 C 运动时,∠BDA 逐渐变 (填“大”或“小”);
(2)判断当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点 D 的运动过程中,△ADE 的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
18.(14分)如图,在平面直角坐标系中,点B为第一象限内一点,点A 为 x 轴正半轴上一点,分别连接OB,AB,△AOB为等边三角形,点 B的横坐标为4.
(1)如图①,求线段 OA的长;
(2)如图②,点M在线段OA上(点M不与点O、点A重合),点N 在线段 BA 的延长线上,连接MB,MN,BM=MN,设OM的长为t,BN的长为d,求d 与t 的关系式(不要求写出 t 的取值范围);
(3)在(2)的条件下,点D为第四象限内一点,分别连接OD,MD,ND,△MND为等边三角形,线段MA的垂直平分线交OD 的延长线于点 E,交MA于点H,连接AE,交ND于点F,连接MF,若 求点 E的横坐标.
1. D 2. D 3. C 4. C 5. A
6. C 解析:如图,过点 P 作 PH⊥MN于点 H,∵ ∠POH=60°,=NH= MN=1.∴OM=OH-MH=4
7. C 解析:如图所示,在 AB 上取点 F',使AF'=AF,过点 C 作 CH⊥AB,垂足为 H.在Rt△ABC中, ∵ EF+CE=EF'+EC,∴当C,E,F'共线,且点 F'与点H重合时,FE+EC的值最小,最小值为
8. C 解析:如图,先作出长方形ABCD,小球从A沿45°角射出,到BC边的E点,AB=BE.从E点沿与 BC 成45°角射出,到AD边的F点,AE=EF.从F点沿与AD成45°角射出,到CD边的G点,DF=DG.从G点沿与DC成45°角射出,到BC边的H点,HF垂直于AD,GC=CH=AB/ .从H点沿与CB成45°角射出,到AD边的M点,EM垂直于AD.从M点沿与DA成45°角射出,到B点,由图可知桌面是2个半以AB为边长的正方形,所以AB:BC=1:2.5=2:5.故选C.
9.1 10.16:25:08 11.10° 12.2a+3b
13.8 解析:如图,延长DE交BC于M,延长AE交BC于N.∵AB=AC,AE平分∠BAC,∴AN⊥BC,BN=CN.∵ ∠DBC=∠D=60°,∴△BDM为等边三角形,∴ BM = DM = BD = 5 cm.∴EM =DM-DE =2cm.∵ △BDM 为等边三角形,∴∠DMB=60°,∴∠NEM= 30°,∴NM EM=1 cm,∴ BNBM-NM=4cm.∴BC=2BN=8cm.
14.48° 解析:延长BA到F,使AF=AC,连接 EF, 如 图 所 示. ∵AB + AC = BE,∴AB+AF = BE = BF,∴ ∠F = ∠BEF = (180°- ∠B ). ∵∠BAD= ∠DAC 9°,AD⊥AE,即∠DAE=90°,∴∠FAE= B4180°-(∠BAD+∠DAE)= 180°-(9°+90°)=81°,∠CAE = ∠DAE-∠DAC = 81°,∴∠FAE = ∠CAE.∵ AF=AC,∠FAE=∠CAE,AE=AE,∴△AFE≌△ACE(SAS),∴∠F=∠ACE.∵ ∠ACE=∠B+∠BAC=∠B+18°,∴∠F=∠B+ 则∠B=48°.
15.(1)如图所示,△A B C 即为所求的三角形.
(2)如图所示,作点A关于直线l的对称点A',连接A'B与直线l交于点 P,则点 P 即为所求.
16.(1)△DBC是等腰直角三角形.理由:∵ ∠ABC=45°,CD⊥AB,∴∠BCD=∠ABC=45°,∴BD=CD,∴△DBC是等腰直角三角形.
(2)∵BE⊥AC,∴∠BDC=∠BEC=90°∵∠BFD=∠CFE,∴∠DBF=∠ACD.在△BDF与△CDA中, ∴ △BDF≌△CDA,∴BF=AC.
(3)∵ BE 是 AC 的垂直平分线,∴ 由(2)知,BF=
17.(1)25 小
(2)当DC=AB=2时,△ABD≌△DCE.理由:∵AB=AC,∴∠B=∠C=40°,∴∠DEC+∠EDC=140°.又∵ ∠ADE=40°,∴ ∠ADB+∠EDC=140°,∴∠ADB=∠DEC.又∵AB=DC=2,∴△ABD≌△DCE.
(3)∵ AB=AC,∴∠B =∠C=40°.①当 AD=AE 时,∠ADE=∠AED=40°,∵∠AED>∠C,∴此时不符合;②当DA=DE时, 40°=100°,∴∠BAD=100°-70°=30°,∴ ∠BDA=180°-30°-40°=110°;③当 EA=ED 时,∠ADE =∠DAE =40°,∴ ∠BAD =100°-40°=60°,∴∠BDA=180°-60°-40°=80°.综上,当∠BDA=110°或80°时,△ADE是等腰三角形.
18.(1)如图①,过点 B 作 BH⊥OA 于点 H,∵ △AOB 为等边三角形,∴BO=BA.∵ BH⊥OA,∴ OH=AH.∵ 点 B 的.横坐标为4,∴OH=4,∴OA=2HO=8.
(2)如图②,过点 M 作 MP ⊥ AB 于点 P,则∠MPA = 90°.∵BM=MN,∴BP=PN.∵ △AOB为等边三角形,∴BA=AO=8, ∴d=8+t.
(3)如图③,过点N作NK∥OB,交x轴于点K,过点N作NR⊥x轴于点R,∵△AOB为等边三角形,∴ ∠BOA=60°=∠OAB.∵NK∥OB,∴∠NKA=∠BOA=60°,且∠OAB=∠NAK=60°,∴∠NAK=∠NKA=60°,∴ △AKN是等边三角形,∴AN=NK=AK.∵△MND为等边三角形,∴ ∠NMD=∠MND=60°,MN=MD,∴∠OMD+∠NMK=∠NMK+∠MNK=180°-60°=120°,..∠OMD=∠MNK.∵AN=BN-AB=8+t-8=t,OM=t,. OM=AN=NK=AK=t,且∠OMD=∠MNK,MD=MN,.△OMD≌△KNM(SAS),.. OD=MK,∠MOD=∠MKN=60°.. MK=8-t+t=8,∴OD=8.∵EH垂直平分MA, 8+t-8=t,∴DE=AN.∵ ∠DOA=∠BAO,∴BN∥OE,∴∠NAF=∠DEF.又∵ ∠AFN = ∠EFD, AN = DE, ∴ △AFN ≌ △EFD(AAS),∴FN=FD.又∵ MN=MD,∴ MF⊥ DN.∵ NR⊥AK,∴∠ARN=90°,且∠NAK=60°,∴∠ANR=30°,∴AR AN 且MF⊥DN,NR⊥AK,∴∠MNR=∠MND=60°,..∠NMA=90°-60°=30°.∵∠BAO=∠AMN+∠ANM,..∠AMN=∠ANM=30°,.. AM= 点E的横坐标为6.
第十三章轴对称提优测试卷
(时间:90分钟 满分:100分)
一、选择题(每小题4分,共32分)
1. 永州市教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育.下列安全图标不是轴对称的是 ( )
2.如图,△ABC与△A'B'C'关于直线MN对称,P为MN上任一点,下列结论中错误的是 ( )
A.△AA'P是等腰三角形
B. MN垂直平分AA',CC'
C.△ABC与△A'B'C'面积相等
D.直线AB,A'B'的交点不一定在直线MN上
3.如图,在△ABC中,AB=AC,AD是BC边上的中线,且BD=BE,∠ADE=20°,则∠BAC的度数为 ( )
A.120° B.110°
C.100° D.90°
4.如图,AD 是△ABC的高,∠BAC=90°,BE 是△ABC的角平分线,交AD于点F,交AC于点E,则下列结论中正确的是 ( )
A. AE=EF B. AF=EF
C. AF=AE D. AE=EC
5.如图,△ABC是等边三角形,AD是角平分线,△ADE是等边三角形,下列结论:①AD⊥BC;②EF=FD;③BE=BD.其中正确的有 ( )
A.3个 B.2个
C.1个 D.0个
6.如图,已知∠AOB=60°,点 P 在边OA上,OP=10,点M,N在边OB上,PM=PN,若MN=2,则OM的长为 ( )
A.2 B.3 C.4 D.5
7.如图,在 Rt△ABC 中,∠ACB=90°,AC=6,BC=8,AB=10,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为 ( )
A B c D.6
8.某台球桌面为如图所示的长方形ABCD,小球从A沿45°角射出,恰好经过5次碰撞到达B处,则AB∶BC等于 ( )
A.1∶2 B.2:3 C.2:5 D.3∶5
二、填空题(每小题4分,共24分)
9.在平面直角坐标系中,已知点A(m,3)与点B(4,n)关于x轴对称,那么(m+n) 的值为 .
10.小明从镜子里看到镜子对面电子钟的像为80:25:21,实际时间是 .
11.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上的A'处,折痕为CD,则∠A'DB的度数为 .
如图,在△ABC中,AB=AC,∠BAC=36°,DE是线段AC的垂直平分线,若BE=a,AE=b,则用含a,b的式子表示△ABC的周长为 .
13.如图,在△ABC 中,AB=AC,D,E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3c m,则BC的长是 cm.
14.如图,已知∠BAD=∠DAC=9°,AD⊥AE,且AB+AC=BE,则∠B= .
三、解答题(共44分)
15.(8分)在如图所示的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在网格中作出△ABC关于直线l对称的△A B C (要求A与A ,B与B ,C与C 相对应);
(2)在直线l上找一点 P,使得PA+PB 的值最小.
16.(10分)如图,在△ABC中,∠ABC=45°,CD⊥AB于点 D,AC的垂直平分线 BE 与 CD交于点 F,与AC交于点 E.
(1)判断△DBC的形状并说明理由;
(2)求证:BF=AC;
(3)试说明:
17.(12分)如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段 BC上运动(D 不与B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点 E.
(1)当∠BDA=115°时,∠BAD= °;点 D从B向 C 运动时,∠BDA 逐渐变 (填“大”或“小”);
(2)判断当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点 D 的运动过程中,△ADE 的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
18.(14分)如图,在平面直角坐标系中,点B为第一象限内一点,点A 为 x 轴正半轴上一点,分别连接OB,AB,△AOB为等边三角形,点 B的横坐标为4.
(1)如图①,求线段 OA的长;
(2)如图②,点M在线段OA上(点M不与点O、点A重合),点N 在线段 BA 的延长线上,连接MB,MN,BM=MN,设OM的长为t,BN的长为d,求d 与t 的关系式(不要求写出 t 的取值范围);
(3)在(2)的条件下,点D为第四象限内一点,分别连接OD,MD,ND,△MND为等边三角形,线段MA的垂直平分线交OD 的延长线于点 E,交MA于点H,连接AE,交ND于点F,连接MF,若 求点 E的横坐标.
1. D 2. D 3. C 4. C 5. A
6. C 解析:如图,过点 P 作 PH⊥MN于点 H,∵ ∠POH=60°,=NH= MN=1.∴OM=OH-MH=4
7. C 解析:如图所示,在 AB 上取点 F',使AF'=AF,过点 C 作 CH⊥AB,垂足为 H.在Rt△ABC中, ∵ EF+CE=EF'+EC,∴当C,E,F'共线,且点 F'与点H重合时,FE+EC的值最小,最小值为
8. C 解析:如图,先作出长方形ABCD,小球从A沿45°角射出,到BC边的E点,AB=BE.从E点沿与 BC 成45°角射出,到AD边的F点,AE=EF.从F点沿与AD成45°角射出,到CD边的G点,DF=DG.从G点沿与DC成45°角射出,到BC边的H点,HF垂直于AD,GC=CH=AB/ .从H点沿与CB成45°角射出,到AD边的M点,EM垂直于AD.从M点沿与DA成45°角射出,到B点,由图可知桌面是2个半以AB为边长的正方形,所以AB:BC=1:2.5=2:5.故选C.
9.1 10.16:25:08 11.10° 12.2a+3b
13.8 解析:如图,延长DE交BC于M,延长AE交BC于N.∵AB=AC,AE平分∠BAC,∴AN⊥BC,BN=CN.∵ ∠DBC=∠D=60°,∴△BDM为等边三角形,∴ BM = DM = BD = 5 cm.∴EM =DM-DE =2cm.∵ △BDM 为等边三角形,∴∠DMB=60°,∴∠NEM= 30°,∴NM EM=1 cm,∴ BNBM-NM=4cm.∴BC=2BN=8cm.
14.48° 解析:延长BA到F,使AF=AC,连接 EF, 如 图 所 示. ∵AB + AC = BE,∴AB+AF = BE = BF,∴ ∠F = ∠BEF = (180°- ∠B ). ∵∠BAD= ∠DAC 9°,AD⊥AE,即∠DAE=90°,∴∠FAE= B4180°-(∠BAD+∠DAE)= 180°-(9°+90°)=81°,∠CAE = ∠DAE-∠DAC = 81°,∴∠FAE = ∠CAE.∵ AF=AC,∠FAE=∠CAE,AE=AE,∴△AFE≌△ACE(SAS),∴∠F=∠ACE.∵ ∠ACE=∠B+∠BAC=∠B+18°,∴∠F=∠B+ 则∠B=48°.
15.(1)如图所示,△A B C 即为所求的三角形.
(2)如图所示,作点A关于直线l的对称点A',连接A'B与直线l交于点 P,则点 P 即为所求.
16.(1)△DBC是等腰直角三角形.理由:∵ ∠ABC=45°,CD⊥AB,∴∠BCD=∠ABC=45°,∴BD=CD,∴△DBC是等腰直角三角形.
(2)∵BE⊥AC,∴∠BDC=∠BEC=90°∵∠BFD=∠CFE,∴∠DBF=∠ACD.在△BDF与△CDA中, ∴ △BDF≌△CDA,∴BF=AC.
(3)∵ BE 是 AC 的垂直平分线,∴ 由(2)知,BF=
17.(1)25 小
(2)当DC=AB=2时,△ABD≌△DCE.理由:∵AB=AC,∴∠B=∠C=40°,∴∠DEC+∠EDC=140°.又∵ ∠ADE=40°,∴ ∠ADB+∠EDC=140°,∴∠ADB=∠DEC.又∵AB=DC=2,∴△ABD≌△DCE.
(3)∵ AB=AC,∴∠B =∠C=40°.①当 AD=AE 时,∠ADE=∠AED=40°,∵∠AED>∠C,∴此时不符合;②当DA=DE时, 40°=100°,∴∠BAD=100°-70°=30°,∴ ∠BDA=180°-30°-40°=110°;③当 EA=ED 时,∠ADE =∠DAE =40°,∴ ∠BAD =100°-40°=60°,∴∠BDA=180°-60°-40°=80°.综上,当∠BDA=110°或80°时,△ADE是等腰三角形.
18.(1)如图①,过点 B 作 BH⊥OA 于点 H,∵ △AOB 为等边三角形,∴BO=BA.∵ BH⊥OA,∴ OH=AH.∵ 点 B 的.横坐标为4,∴OH=4,∴OA=2HO=8.
(2)如图②,过点 M 作 MP ⊥ AB 于点 P,则∠MPA = 90°.∵BM=MN,∴BP=PN.∵ △AOB为等边三角形,∴BA=AO=8, ∴d=8+t.
(3)如图③,过点N作NK∥OB,交x轴于点K,过点N作NR⊥x轴于点R,∵△AOB为等边三角形,∴ ∠BOA=60°=∠OAB.∵NK∥OB,∴∠NKA=∠BOA=60°,且∠OAB=∠NAK=60°,∴∠NAK=∠NKA=60°,∴ △AKN是等边三角形,∴AN=NK=AK.∵△MND为等边三角形,∴ ∠NMD=∠MND=60°,MN=MD,∴∠OMD+∠NMK=∠NMK+∠MNK=180°-60°=120°,..∠OMD=∠MNK.∵AN=BN-AB=8+t-8=t,OM=t,. OM=AN=NK=AK=t,且∠OMD=∠MNK,MD=MN,.△OMD≌△KNM(SAS),.. OD=MK,∠MOD=∠MKN=60°.. MK=8-t+t=8,∴OD=8.∵EH垂直平分MA, 8+t-8=t,∴DE=AN.∵ ∠DOA=∠BAO,∴BN∥OE,∴∠NAF=∠DEF.又∵ ∠AFN = ∠EFD, AN = DE, ∴ △AFN ≌ △EFD(AAS),∴FN=FD.又∵ MN=MD,∴ MF⊥ DN.∵ NR⊥AK,∴∠ARN=90°,且∠NAK=60°,∴∠ANR=30°,∴AR AN 且MF⊥DN,NR⊥AK,∴∠MNR=∠MND=60°,..∠NMA=90°-60°=30°.∵∠BAO=∠AMN+∠ANM,..∠AMN=∠ANM=30°,.. AM= 点E的横坐标为6.
