13.1 轴对称第1课时 轴对称 同步练习(含答案) 2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 13.1 轴对称第1课时 轴对称 同步练习(含答案) 2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 788.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 21:30:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
13.1 轴 对 称
第1课时 轴 对 称
1.下面四幅图是我国传统文化与艺术中的几个经典图案,其中不是轴对称图形的是( )
2.如图所示的图形中,左边的图形与右边的图形成轴对称的是 ( )
3.如图,由“ ”和“□”组成轴对称图形,该图形的对称轴是直线 ( )
A. l B. l C. l D. l
4.如图,若△ABC 与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法不一定正确的是 ( )
B. BO=B'O
C. AA'⊥MN D. AB∥B'C
5.如图,△ABC和△A'B'C'关于直线MN对称,若∠A=30°,∠C'=60°,则∠B 的度数是 ;若AB=5,BC=3,A'C'的取值范围是 .
6. 如图,已知直线AD 是△ABC 的对称轴,若BD=4,AD=6,则图中阴影部分的面积是 .
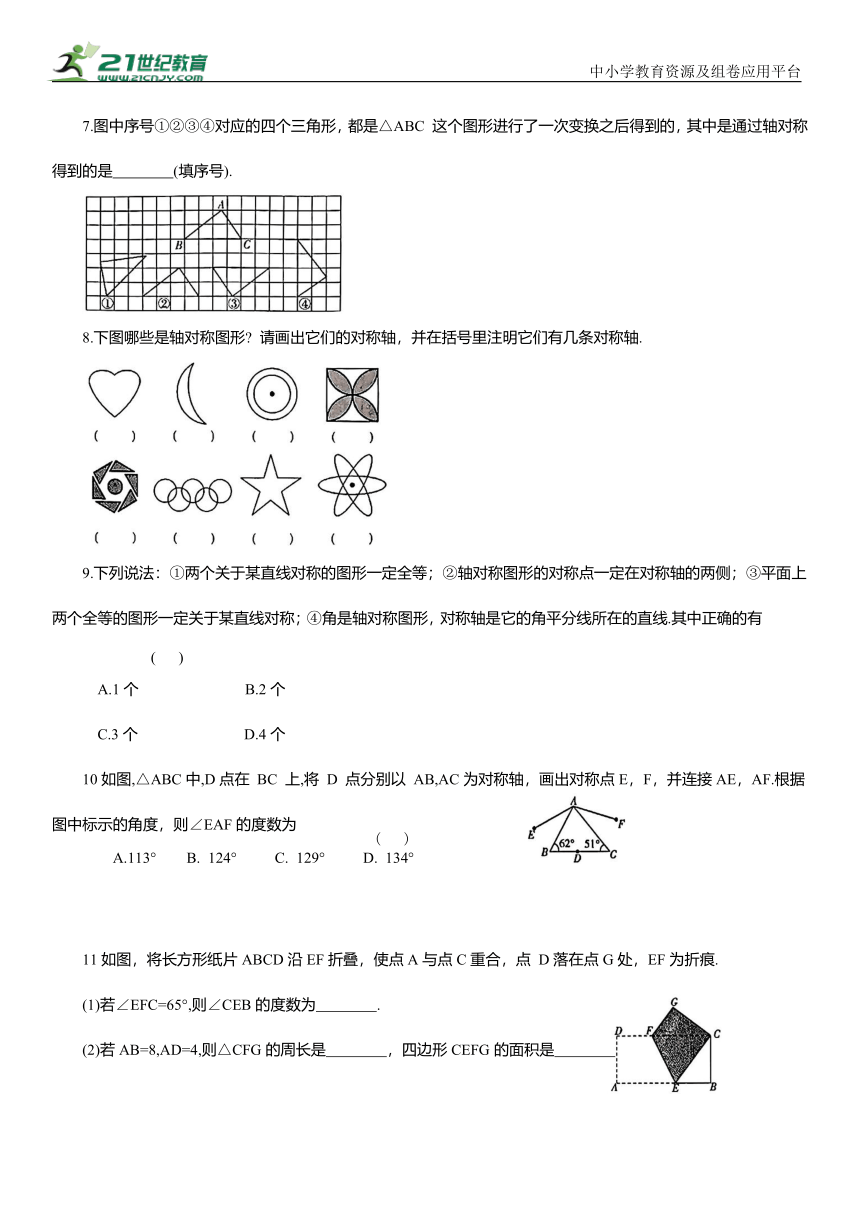
7.图中序号①②③④对应的四个三角形,都是△ABC 这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是 (填序号).
8.下图哪些是轴对称图形 请画出它们的对称轴,并在括号里注明它们有几条对称轴.
9.下列说法:①两个关于某直线对称的图形一定全等;②轴对称图形的对称点一定在对称轴的两侧;③平面上两个全等的图形一定关于某直线对称;④角是轴对称图形,对称轴是它的角平分线所在的直线.其中正确的有 ( )
A.1个 B.2个
C.3个 D.4个
10如图,△ABC中,D点在 BC 上,将 D 点分别以 AB,AC为对称轴,画出对称点E,F,并连接AE,AF.根据图中标示的角度,则∠EAF的度数为
A.113° B. 124° C. 129° D. 134°
11如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点 D落在点G处,EF为折痕.
(1)若∠EFC=65°,则∠CEB的度数为 .
(2)若AB=8,AD=4,则△CFG的周长是 ,四边形CEFG的面积是
12. 常见的正多边形有等边三角形、正方形、正五边形、正六边形等,如图所示.
(1)画出等边三角形、正方形、正五边形、正六边形所有的对称轴;
(2)请你猜想,正十二边形有几条对称轴,正n边形呢
13.如图,△ABC和△A'B'C'关于直线m对称.
(1)结合图形写出对称点.
(2)△ABC和△A'B'C'有什么关系 若∠A=32°, ,求∠C'的度数.
(3)分别连接AA',BB',CC',直线 m 与线段AA',BB',CC'有什么关系 线段AA',BB',CC'之间有什么关系
(4)延长线段AC与A'C',它们的交点与直线 m有怎样的关系 其他对应线段(或其延长线)的交点呢 你发现了什么规律,请叙述出来与同伴交流.
14.小华在镜中看到身后墙上的钟,则实际时间最接近8点的是 ( )
15.如图,在△ABC中,∠C=90°,点A关于 BC边的对称点为A',点 B关于AC边的对称点为B',点C关于AB边的对称点为 C',则 S△ABC与 S△A'B'C'的比值为 .
16.小玉学了轴对称后,想起以前做过的一道题:有一组数排成如图所示的方阵,试计算这组数的和.小玉想:方阵就像正方形,正方形是轴对称图形,能不能利用轴对称的思想来解决方阵的计算问题呢 小玉试了试,得到了非常巧妙的方法,你也来试试看吧!
第 1课时 轴 对 称
1. D 2. A 3. C 4. D 5.90° 29. B 解析:①④正确.
10. D
11.(1)50°
(2)12 16 解析:由折叠可知,GF=DF,△CFG的周长=GF+FC+CG=AB+AD=12;易得△FGC≌△EBC,∴四边形 ECGF的面积=四边形 EADF 的面积=四边形EBCF 的面积=四边形ABCD面积的一半,S四边形CEFC=16.
12.(1)画出的对称轴如图所示.
(2)由(1)可知,正多边形对称轴的条数与正多边形的边数相等,所以正十二边形有12条对称轴,正n边形有n条对称轴.
13.(1)对称点有A和A',B和B',C和C'.
(2)由题意△ABC≌△A'B'C'(合理即可).在△A'B'C'中,∠A'= .
(3)直线m垂直平分线段AA',BB',CC',AA'∥BB'∥CC'.
(4)延长线段AC与A'C',它们的交点在直线m上,其他对应线段(或其延长线)的交点也在直线m上.规律:若两条线段关于直线m对称,且不平行,则它们的交点或它们的延长线的交点在对称轴m上.
14. D 解析:根据镜面对称的性质,在平面镜中的钟面上的时针、分针的位置和实物应关于过12时、6时的直线成轴对称.8点的对称点是4点,那么8点的时钟在镜子中看来应该是4点的样子,所以选D.
15 解析:如图,连接C'C交AB于E,延长 C' C 交 A' B'于点 D,连接 CB',CA',AC'.由题意得AC=A'C,BC=B'C,∠ACB = ∠A'CB',AB 垂直平分 CC',∴△ABC ≌ △A′ B′ C ( SAS ),∴S△ABC= S△A'B'C, ∠BAC = ∠AA' B',AB=A'B',∴AB∥A'B',∴CD⊥A'B',∴根据全等三角形对应边上的高相等,可得 与S△A'B'C'的比值为-
16.从方阵中的数可以看出,一条对角线上的数都是5,若把这条对角线当成对称轴,把正方形对折一下,则对应点位置上的两数之和都是10,如图所示,则这个方阵中的所有数的和为10×10+5×5=125.
13.1 轴 对 称
第1课时 轴 对 称
1.下面四幅图是我国传统文化与艺术中的几个经典图案,其中不是轴对称图形的是( )
2.如图所示的图形中,左边的图形与右边的图形成轴对称的是 ( )
3.如图,由“ ”和“□”组成轴对称图形,该图形的对称轴是直线 ( )
A. l B. l C. l D. l
4.如图,若△ABC 与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法不一定正确的是 ( )
B. BO=B'O
C. AA'⊥MN D. AB∥B'C
5.如图,△ABC和△A'B'C'关于直线MN对称,若∠A=30°,∠C'=60°,则∠B 的度数是 ;若AB=5,BC=3,A'C'的取值范围是 .
6. 如图,已知直线AD 是△ABC 的对称轴,若BD=4,AD=6,则图中阴影部分的面积是 .
7.图中序号①②③④对应的四个三角形,都是△ABC 这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是 (填序号).
8.下图哪些是轴对称图形 请画出它们的对称轴,并在括号里注明它们有几条对称轴.
9.下列说法:①两个关于某直线对称的图形一定全等;②轴对称图形的对称点一定在对称轴的两侧;③平面上两个全等的图形一定关于某直线对称;④角是轴对称图形,对称轴是它的角平分线所在的直线.其中正确的有 ( )
A.1个 B.2个
C.3个 D.4个
10如图,△ABC中,D点在 BC 上,将 D 点分别以 AB,AC为对称轴,画出对称点E,F,并连接AE,AF.根据图中标示的角度,则∠EAF的度数为
A.113° B. 124° C. 129° D. 134°
11如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点 D落在点G处,EF为折痕.
(1)若∠EFC=65°,则∠CEB的度数为 .
(2)若AB=8,AD=4,则△CFG的周长是 ,四边形CEFG的面积是
12. 常见的正多边形有等边三角形、正方形、正五边形、正六边形等,如图所示.
(1)画出等边三角形、正方形、正五边形、正六边形所有的对称轴;
(2)请你猜想,正十二边形有几条对称轴,正n边形呢
13.如图,△ABC和△A'B'C'关于直线m对称.
(1)结合图形写出对称点.
(2)△ABC和△A'B'C'有什么关系 若∠A=32°, ,求∠C'的度数.
(3)分别连接AA',BB',CC',直线 m 与线段AA',BB',CC'有什么关系 线段AA',BB',CC'之间有什么关系
(4)延长线段AC与A'C',它们的交点与直线 m有怎样的关系 其他对应线段(或其延长线)的交点呢 你发现了什么规律,请叙述出来与同伴交流.
14.小华在镜中看到身后墙上的钟,则实际时间最接近8点的是 ( )
15.如图,在△ABC中,∠C=90°,点A关于 BC边的对称点为A',点 B关于AC边的对称点为B',点C关于AB边的对称点为 C',则 S△ABC与 S△A'B'C'的比值为 .
16.小玉学了轴对称后,想起以前做过的一道题:有一组数排成如图所示的方阵,试计算这组数的和.小玉想:方阵就像正方形,正方形是轴对称图形,能不能利用轴对称的思想来解决方阵的计算问题呢 小玉试了试,得到了非常巧妙的方法,你也来试试看吧!
第 1课时 轴 对 称
1. D 2. A 3. C 4. D 5.90° 2
10. D
11.(1)50°
(2)12 16 解析:由折叠可知,GF=DF,△CFG的周长=GF+FC+CG=AB+AD=12;易得△FGC≌△EBC,∴四边形 ECGF的面积=四边形 EADF 的面积=四边形EBCF 的面积=四边形ABCD面积的一半,S四边形CEFC=16.
12.(1)画出的对称轴如图所示.
(2)由(1)可知,正多边形对称轴的条数与正多边形的边数相等,所以正十二边形有12条对称轴,正n边形有n条对称轴.
13.(1)对称点有A和A',B和B',C和C'.
(2)由题意△ABC≌△A'B'C'(合理即可).在△A'B'C'中,∠A'= .
(3)直线m垂直平分线段AA',BB',CC',AA'∥BB'∥CC'.
(4)延长线段AC与A'C',它们的交点在直线m上,其他对应线段(或其延长线)的交点也在直线m上.规律:若两条线段关于直线m对称,且不平行,则它们的交点或它们的延长线的交点在对称轴m上.
14. D 解析:根据镜面对称的性质,在平面镜中的钟面上的时针、分针的位置和实物应关于过12时、6时的直线成轴对称.8点的对称点是4点,那么8点的时钟在镜子中看来应该是4点的样子,所以选D.
15 解析:如图,连接C'C交AB于E,延长 C' C 交 A' B'于点 D,连接 CB',CA',AC'.由题意得AC=A'C,BC=B'C,∠ACB = ∠A'CB',AB 垂直平分 CC',∴△ABC ≌ △A′ B′ C ( SAS ),∴S△ABC= S△A'B'C, ∠BAC = ∠AA' B',AB=A'B',∴AB∥A'B',∴CD⊥A'B',∴根据全等三角形对应边上的高相等,可得 与S△A'B'C'的比值为-
16.从方阵中的数可以看出,一条对角线上的数都是5,若把这条对角线当成对称轴,把正方形对折一下,则对应点位置上的两数之和都是10,如图所示,则这个方阵中的所有数的和为10×10+5×5=125.
