13.2 画轴对称图形第1课时 画轴对称图形 同步练习 2024-2025学年人教版八年级数学上册(含答案)
文档属性
| 名称 | 13.2 画轴对称图形第1课时 画轴对称图形 同步练习 2024-2025学年人教版八年级数学上册(含答案) | 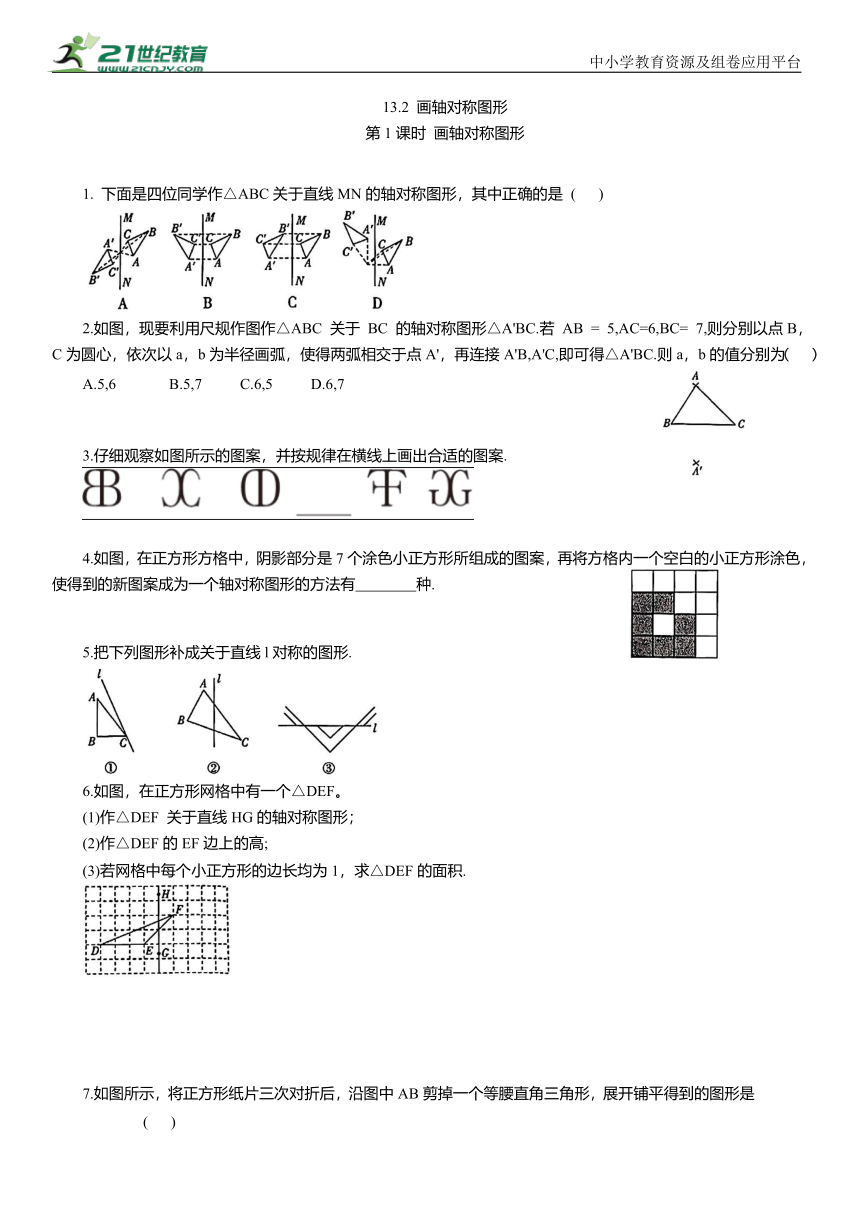 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 12:45:37 | ||
图片预览


文档简介
13.2 画轴对称图形
第1课时 画轴对称图形
1. 下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是 ( )
2.如图,现要利用尺规作图作△ABC 关于 BC 的轴对称图形△A'BC.若 AB = 5,AC=6,BC= 7,则分别以点B,C为圆心,依次以a,b为半径画弧,使得两弧相交于点A',再连接A'B,A'C,即可得△A'BC.则a,b的值分别为
A.5,6 B.5,7 C.6,5 D.6,7
3.仔细观察如图所示的图案,并按规律在横线上画出合适的图案.
4.如图,在正方形方格中,阴影部分是7个涂色小正方形所组成的图案,再将方格内一个空白的小正方形涂色,使得到的新图案成为一个轴对称图形的方法有 种.
5.把下列图形补成关于直线l对称的图形.
6.如图,在正方形网格中有一个△DEF。
(1)作△DEF 关于直线HG的轴对称图形;
(2)作△DEF的EF边上的高;
(3)若网格中每个小正方形的边长均为1,求△DEF的面积.
7.如图所示,将正方形纸片三次对折后,沿图中AB剪掉一个等腰直角三角形,展开铺平得到的图形是 ( )
8.在如图所示的正方形网格中画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有 ( )
A.2条 B.3条 C.4条 D.5条
如图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是 .
10图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,线段 OM,ON的端点均在格点上.已知OM=ON,在图①、图②给定的网格中以OM,ON为邻边各画一个四边形,使第四个顶点在格点上.
要求:(1)所画的两个四边形均是轴对称图形.
(2)所画的两个四边形不全等.
11.如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形,并画出相应的对称轴.
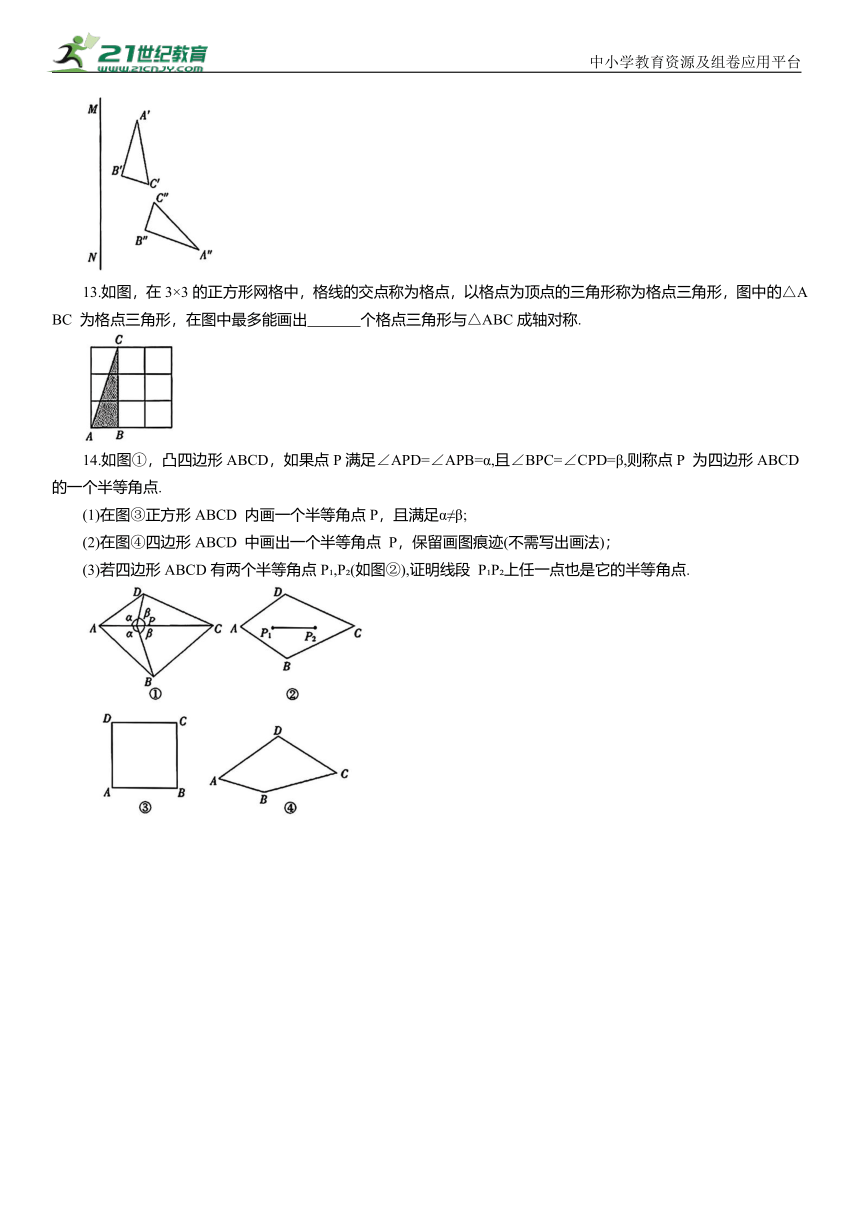
12.如图,△ABC与△A'B'C'关于直线MN对称,△A'B'C'与△A"B"C"关于直线 EF 对称.
(1)画出△ABC 和直线 EF;
(2)若直线 MN和EF 相交于点 O,直线MN,EF所夹的锐角设为α,猜想∠BOB"与α之间的数量关系,并说明理由.
13.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC 为格点三角形,在图中最多能画出 个格点三角形与△ABC成轴对称.
14.如图①,凸四边形ABCD,如果点P满足∠APD=∠APB=α,且∠BPC=∠CPD=β,则称点P 为四边形ABCD 的一个半等角点.
(1)在图③正方形ABCD 内画一个半等角点P,且满足α≠β;
(2)在图④四边形ABCD 中画出一个半等角点 P,保留画图痕迹(不需写出画法);
(3)若四边形ABCD有两个半等角点P ,P (如图②),证明线段 P P 上任一点也是它的半等角点.
中小学教育资源及组卷应用平台
第1 课时 画轴对称图形
1. B 2. A3.HE 4.3
5.如图所示.
6.(1)如图所示,△D'E'F'即为所求.
(2)如图所示,DM为EF边上的高.
7. A
8. C 解析:如图所示,能满足条件的线段有4条.
9.① 解析:如图,球最后落入①号球洞.
10.如图所示.
11. 如图所示.
12.(1)如图,作出A',B',C'关于直线MN的对称点A,B. C,连接AB,BC,AC,即可得到△ABC,再连接B'B",作线段 B'B"的垂直平分线EF,则直线 EF 是△A'B'C'和△A"B"C"的对称轴.
理由:如图,连接BO,B'O,B"O.∵ △ABC 和△A'B'C'关于直线MN对称,..∠BOM=∠B'OM.又∵ △A'B'C'和△A"B"C"关于直线 EF 对称,.. ∠B'OE=∠B"OE, .∠BOB"=∠BOM+∠B'OM+∠B'OE+∠B"OE=2(∠B'OM+∠B'OE)=2α,即∠BOB"=2α.
13.6 解析:如图,最多能画出6个格点三角形与△ABC成轴对称.
14.(1)所画的点P在AC上,且不是AC的中点和AC的端点即可(画图略).
(2)连接AC,作点B关于AC的对称点 B',连接并延长DB'交AC于点 P,点P即为所求,如图①所示.
(3)如图②,连接P A,P D,P B,P C,P D和P B,根据题意,得∠AP D=∠AP B,∠DP C=∠BP C,∴∠AP B+∠BP C=180°,
∴P 在AC 上,同理,P 也在 AC 上.在△DP P 和△BP P 中,
. △DP P ≌△BP P .∴DP =BP ,DP =
BP ,于是B,D 关于AC对称.设P 是P P 上任一点,连接PD,PB,由对称性,得∠DPA=∠BPA,∠DPC=∠BPC,∴点P是四边形ABCD的半等角点,即线段P P 上任一点都是四边形ABCD的半等角点.
第1课时 画轴对称图形
1. 下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是 ( )
2.如图,现要利用尺规作图作△ABC 关于 BC 的轴对称图形△A'BC.若 AB = 5,AC=6,BC= 7,则分别以点B,C为圆心,依次以a,b为半径画弧,使得两弧相交于点A',再连接A'B,A'C,即可得△A'BC.则a,b的值分别为
A.5,6 B.5,7 C.6,5 D.6,7
3.仔细观察如图所示的图案,并按规律在横线上画出合适的图案.
4.如图,在正方形方格中,阴影部分是7个涂色小正方形所组成的图案,再将方格内一个空白的小正方形涂色,使得到的新图案成为一个轴对称图形的方法有 种.
5.把下列图形补成关于直线l对称的图形.
6.如图,在正方形网格中有一个△DEF。
(1)作△DEF 关于直线HG的轴对称图形;
(2)作△DEF的EF边上的高;
(3)若网格中每个小正方形的边长均为1,求△DEF的面积.
7.如图所示,将正方形纸片三次对折后,沿图中AB剪掉一个等腰直角三角形,展开铺平得到的图形是 ( )
8.在如图所示的正方形网格中画有两条线段.现在要再画一条,使图中的三条线段组成一个轴对称图形,能满足条件的线段有 ( )
A.2条 B.3条 C.4条 D.5条
如图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是 .
10图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,线段 OM,ON的端点均在格点上.已知OM=ON,在图①、图②给定的网格中以OM,ON为邻边各画一个四边形,使第四个顶点在格点上.
要求:(1)所画的两个四边形均是轴对称图形.
(2)所画的两个四边形不全等.
11.如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形,并画出相应的对称轴.
12.如图,△ABC与△A'B'C'关于直线MN对称,△A'B'C'与△A"B"C"关于直线 EF 对称.
(1)画出△ABC 和直线 EF;
(2)若直线 MN和EF 相交于点 O,直线MN,EF所夹的锐角设为α,猜想∠BOB"与α之间的数量关系,并说明理由.
13.如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC 为格点三角形,在图中最多能画出 个格点三角形与△ABC成轴对称.
14.如图①,凸四边形ABCD,如果点P满足∠APD=∠APB=α,且∠BPC=∠CPD=β,则称点P 为四边形ABCD 的一个半等角点.
(1)在图③正方形ABCD 内画一个半等角点P,且满足α≠β;
(2)在图④四边形ABCD 中画出一个半等角点 P,保留画图痕迹(不需写出画法);
(3)若四边形ABCD有两个半等角点P ,P (如图②),证明线段 P P 上任一点也是它的半等角点.
中小学教育资源及组卷应用平台
第1 课时 画轴对称图形
1. B 2. A3.HE 4.3
5.如图所示.
6.(1)如图所示,△D'E'F'即为所求.
(2)如图所示,DM为EF边上的高.
7. A
8. C 解析:如图所示,能满足条件的线段有4条.
9.① 解析:如图,球最后落入①号球洞.
10.如图所示.
11. 如图所示.
12.(1)如图,作出A',B',C'关于直线MN的对称点A,B. C,连接AB,BC,AC,即可得到△ABC,再连接B'B",作线段 B'B"的垂直平分线EF,则直线 EF 是△A'B'C'和△A"B"C"的对称轴.
理由:如图,连接BO,B'O,B"O.∵ △ABC 和△A'B'C'关于直线MN对称,..∠BOM=∠B'OM.又∵ △A'B'C'和△A"B"C"关于直线 EF 对称,.. ∠B'OE=∠B"OE, .∠BOB"=∠BOM+∠B'OM+∠B'OE+∠B"OE=2(∠B'OM+∠B'OE)=2α,即∠BOB"=2α.
13.6 解析:如图,最多能画出6个格点三角形与△ABC成轴对称.
14.(1)所画的点P在AC上,且不是AC的中点和AC的端点即可(画图略).
(2)连接AC,作点B关于AC的对称点 B',连接并延长DB'交AC于点 P,点P即为所求,如图①所示.
(3)如图②,连接P A,P D,P B,P C,P D和P B,根据题意,得∠AP D=∠AP B,∠DP C=∠BP C,∴∠AP B+∠BP C=180°,
∴P 在AC 上,同理,P 也在 AC 上.在△DP P 和△BP P 中,
. △DP P ≌△BP P .∴DP =BP ,DP =
BP ,于是B,D 关于AC对称.设P 是P P 上任一点,连接PD,PB,由对称性,得∠DPA=∠BPA,∠DPC=∠BPC,∴点P是四边形ABCD的半等角点,即线段P P 上任一点都是四边形ABCD的半等角点.
