第十二章全等三角形复习练习 2024-2025学年人教版八年级数学上册(含答案)
文档属性
| 名称 | 第十二章全等三角形复习练习 2024-2025学年人教版八年级数学上册(含答案) | 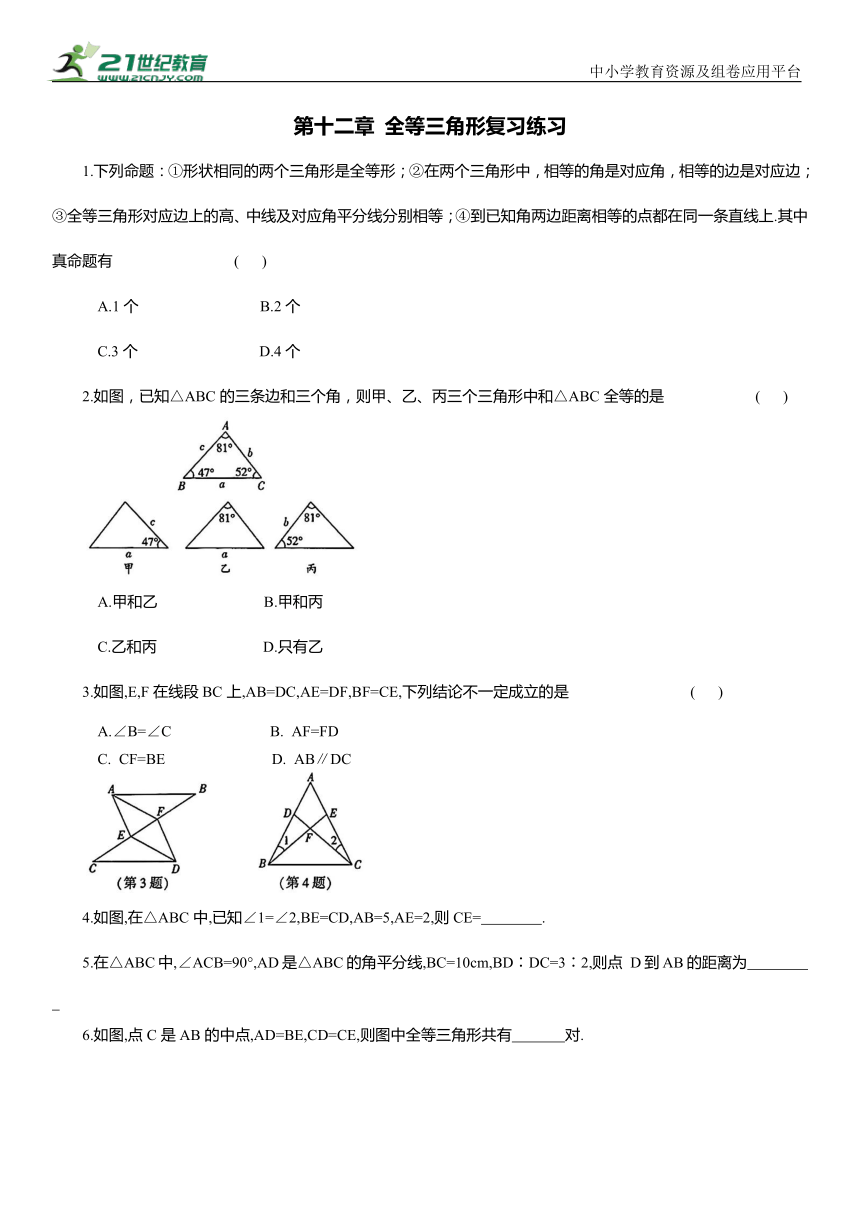 | |
| 格式 | docx | ||
| 文件大小 | 603.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 12:56:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
全等三角形复习练习
1.下列命题:①形状相同的两个三角形是全等形;②在两个三角形中,相等的角是对应角,相等的边是对应边;③全等三角形对应边上的高、中线及对应角平分线分别相等;④到已知角两边距离相等的点都在同一条直线上.其中真命题有 ( )
A.1个 B.2个
C.3个 D.4个
2.如图,已知△ABC的三条边和三个角,则甲、乙、丙三个三角形中和△ABC全等的是 ( )
A.甲和乙 B.甲和丙
C.乙和丙 D.只有乙
3.如图,E,F在线段BC上,AB=DC,AE=DF,BF=CE,下列结论不一定成立的是 ( )
A.∠B=∠C B. AF=FD
C. CF=BE D. AB∥DC
4.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= .
5.在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD∶DC=3∶2,则点 D到AB的距离为
6.如图,点C是AB的中点,AD=BE,CD=CE,则图中全等三角形共有 对.
7.如图,在直线MN上求作一点P,使点 P到射线 OA和OB的距离相等.(要求尺规作图,不写作法,但要保留作图痕迹)
8.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
9.如图,O 是△ABC 的角平分线的交点,△ABC的面积为2,周长为4,则点O到BC的距离为( )
A.1 B.2
C.3 D.无法确定
10.如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,得不到全等三角形纸片的是 ( )
11.如图,已知△ABC的面积为8,BP 为∠ABC 的平分线,AP⊥BP于点P,则△BCP的面积为 ( )
A.3.5 B.3.9 C.4 D.4.2
12.如图,A,C,N三点在同一直线上,在△ABC中,∠A:∠ABC∶∠ACB=3∶5∶10,若△MNC≌△ABC,则∠BCM:∠BCN= .
13.在平面直角坐标系xOy中,A(0,2),B(4,0),点 P与A,B不重合.若以P,O,B三点为顶点的三角形与△ABO全等,则点 P的坐标为 .
14.如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连接BE,且BE平分∠ABC,以下命题:①BC+AD=AB;②E为 CD 中点;③∠AEB=90° 其中正确的有 .(填序号)
15.如图是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B 到地面的距离 BD=3 m.小亮在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=2m,点A到地面的距离AE=1.8 m;当他从A处摆动到A'处时,有A'B⊥AB.
(1)求A'到BD的距离;
(2)求A'到地面的距离.
16. 如图,在△ABC中,AD平分∠BAC,DG⊥BC,G是BC的中点,DE⊥AB于E,DF⊥AC于 F.
(1)求证:BE=CF;
(2)如果AB=16,AC=10,求AE的长.
17.如图①,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA 的平分线,AD,CE 相交于点 F.
(1)直接写出∠AFC的度数;
(2)请你判断并写出EF 与DF之间的数量关系;
(3)如图②,在△ABC中,如果∠ACB不是直角,其他条件不变,试判断线段AE,CD与AC之间的数量关系,并说明理由.
1. B 2. B 3. B 4.3 5.4 cm 6.4
7. 如图.
8.(1)∵AD∥BE,∴∠A=∠B.在△ACD 和△BEC中, ∴△ACD≌△BEC(SAS).
(2)∵△ACD≌△BEC,∴CD=CE.∵ CF 平分∠DCE,∴∠DCF=∠ECF.在 △DCF 和 △ECF 中, ∴ △DCF≌△ECF,∴∠DFC=∠EFC.∵ ∠DFC+∠EFC=180°,∴ ∠DFC=∠EFC=90°,∴CF⊥DE.
9. A 解析:连接AO,BO,CO.∵O是△ABC的角平分线的交点,∴三个小三角形的高相等(设高为x,),底边之和为4,. 解得x=1.
10. C 解析:如图,∵ ∠DEC=∠B+∠BDE, ∴x°+∠FEC=x°+∠BDE,∴∠FEC=∠BDE,∴其对应边应该是BE和CF,而已知给的是BD=FC=3,∴不能判定两个小三角形全等,故选 C.
11. C 解析:如图,延长AP交BC的延长线于E,由题意得∠APB = ∠BPE = 90°,∠ABP =∠EBP.由 ASA得△ABP≌△EBP,∴S△ABP=S△BEP,AP=PE,∴△APC 和△CPE等底同高, 设 △ACE 的 面 积 为 m,
12.1:4 解析:∵ ∠A:∠ABC:∠ACB=3:5:10,∴∠A=30°,∠ABC=50°,∠ACB=100°.∵△MNC≌△ABC,∴∠N=∠ABC=50°,∠M=∠A=30°,∴∠MCA=∠M+∠N=80°,∴∠BCM=20°,∠BCN=80°,∴∠BCM∶∠BCN=1∶4.
13.(0,-2)或(4,-2)或(4,2) 解析:点P的位置如图所示.
14.①②③④ 解析:∵ AD∥BC,∴∠ABC+∠BAD=180°.∵ AE,BE分别是∠BAD与∠ABC的平分线,∴ ∴∠AEB=180°-(∠BAE+∠ABE)=90°,故③正确.
延长AE交BC的延长线于F,如图,∵∠AEB=90°,∴BE⊥AF.∵ BE平分∠ABC,∴∠ABE=∠FBE.
∵∠ABE=∠FBE,BE=BE,∠AEB=∠FEB,∴ △ABE≌△FBE(ASA),∴AB=BF,AE=FE.∵ AD∥BC,∴∠EAD=∠F∴∠EAD=∠F,AE=FE,∠AED=∠FEC,∴△ADE≌△FCE(ASA),∴AD=CF,∴AB=BF=BC+CF=BC+AD,故①正确.∵ △ADE≌△FCE,∴DE=CE,
即点 E 为 CD 的中点,故②正确.∵ △ADE≌△FCE,∴ S△ADE = S四边形ABCD故④正确.
15.(1)如图,作A'F⊥BD,垂足为F.∵AC⊥BD,∴∠ACB=∠A'FB=90°,∴∠1+∠3=90°.又∵A'B⊥AB,∴∠1+∠2=90°,∴∠2=∠3.在△ACB 和△BFA'中, . △ACB≌△BFA'(AAS),∴A'F=BC.由题意 AC∥DE 且 CD⊥AC,AE⊥DE,∴CD=AE=1.8 m,∴BC=BD-CD=3-1.8=1.2(m),∴A'F=1.2m ,即A'到BD的距离是1.2m.
(2)由(1)知△ACB≌△BFA',∴BF=AC=2m.如图,作A'H⊥DE,垂足为H.∵A'F∥DE,∴A'H=FD,∴A'H=BD-BF=3-2=1(m),即A'到地面的距离是1m.
16.(1)如图,连接BD,CD.∵ DG⊥BC,BG=GC,∴由三角形全等可知DB=DC.∵ AD 平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF.在Rt△DEB和Rt△DFC 中, ∴ Rt△DEB≌Rt△DFC(HL),∴BE=CF.
(2)在 Rt△ADE 和Rt△ADF中, . Rt△ADE≌Rt△ADF(HL),∴AE=AF,∴AB-BE=AC+CF,∴2BE=AB-AC=16-10=6,∴BE=3.∴AE=AB-BE=16-3=13.
17. (1)120°.
(2)EF与DF之间的数量关系为EF=DF.理由:如图①,在AC 上截取 CG=CD,连接GF.∵CE是∠BCA的平分线,∴∠DCF=∠GCF.在△CFG 和△CFD中, ∴ △CFG ≌△CFD(SAS),∴GF=DF,∠CFD=∠CFG.∵ ∠B=60°,AD,CE分别是∠BAC,∠BCA 的平分线,∴ 且∠EAF=∠GAF,∴∠FAC+∠FCA= (∠BAC∠ACB) (180°-∠B)=60°,∴∠AFC=120°,∴∠CFD=60°∠CFG,∴ ∠AFG =60°.又∵ ∠AFE = ∠CFD=60°,∴ ∠AFE =∠AFG.在△AFE和△AFG中, ∴△AFE≌△AFG(ASA),∴EF=GF,∴DF=EF.
(3)AC=AE+CD.理由:如图②,在AC上截取 AG =AE,连接 GF.在 △EAF 和△GAF 中、△GAF(SAS),∴∠EFA=∠GFA.又由题可 A知, ∴∠AFC=180°-(∠FAC+∠FCA)= 120°,∴∠EFA=∠GFA=180°-120°=60°=∠DFC,∴∠CFG=∠CFD=60°.在△FDC 和△FGC中. . △FDC≌△FGC(ASA),∴CD=CG,∴AC=AG+CG=AE+CD.
全等三角形复习练习
1.下列命题:①形状相同的两个三角形是全等形;②在两个三角形中,相等的角是对应角,相等的边是对应边;③全等三角形对应边上的高、中线及对应角平分线分别相等;④到已知角两边距离相等的点都在同一条直线上.其中真命题有 ( )
A.1个 B.2个
C.3个 D.4个
2.如图,已知△ABC的三条边和三个角,则甲、乙、丙三个三角形中和△ABC全等的是 ( )
A.甲和乙 B.甲和丙
C.乙和丙 D.只有乙
3.如图,E,F在线段BC上,AB=DC,AE=DF,BF=CE,下列结论不一定成立的是 ( )
A.∠B=∠C B. AF=FD
C. CF=BE D. AB∥DC
4.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE= .
5.在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=10cm,BD∶DC=3∶2,则点 D到AB的距离为
6.如图,点C是AB的中点,AD=BE,CD=CE,则图中全等三角形共有 对.
7.如图,在直线MN上求作一点P,使点 P到射线 OA和OB的距离相等.(要求尺规作图,不写作法,但要保留作图痕迹)
8.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
9.如图,O 是△ABC 的角平分线的交点,△ABC的面积为2,周长为4,则点O到BC的距离为( )
A.1 B.2
C.3 D.无法确定
10.如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,得不到全等三角形纸片的是 ( )
11.如图,已知△ABC的面积为8,BP 为∠ABC 的平分线,AP⊥BP于点P,则△BCP的面积为 ( )
A.3.5 B.3.9 C.4 D.4.2
12.如图,A,C,N三点在同一直线上,在△ABC中,∠A:∠ABC∶∠ACB=3∶5∶10,若△MNC≌△ABC,则∠BCM:∠BCN= .
13.在平面直角坐标系xOy中,A(0,2),B(4,0),点 P与A,B不重合.若以P,O,B三点为顶点的三角形与△ABO全等,则点 P的坐标为 .
14.如图,在四边形ABCD中,AD∥BC,若∠DAB的平分线AE交CD于E,连接BE,且BE平分∠ABC,以下命题:①BC+AD=AB;②E为 CD 中点;③∠AEB=90° 其中正确的有 .(填序号)
15.如图是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B 到地面的距离 BD=3 m.小亮在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=2m,点A到地面的距离AE=1.8 m;当他从A处摆动到A'处时,有A'B⊥AB.
(1)求A'到BD的距离;
(2)求A'到地面的距离.
16. 如图,在△ABC中,AD平分∠BAC,DG⊥BC,G是BC的中点,DE⊥AB于E,DF⊥AC于 F.
(1)求证:BE=CF;
(2)如果AB=16,AC=10,求AE的长.
17.如图①,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA 的平分线,AD,CE 相交于点 F.
(1)直接写出∠AFC的度数;
(2)请你判断并写出EF 与DF之间的数量关系;
(3)如图②,在△ABC中,如果∠ACB不是直角,其他条件不变,试判断线段AE,CD与AC之间的数量关系,并说明理由.
1. B 2. B 3. B 4.3 5.4 cm 6.4
7. 如图.
8.(1)∵AD∥BE,∴∠A=∠B.在△ACD 和△BEC中, ∴△ACD≌△BEC(SAS).
(2)∵△ACD≌△BEC,∴CD=CE.∵ CF 平分∠DCE,∴∠DCF=∠ECF.在 △DCF 和 △ECF 中, ∴ △DCF≌△ECF,∴∠DFC=∠EFC.∵ ∠DFC+∠EFC=180°,∴ ∠DFC=∠EFC=90°,∴CF⊥DE.
9. A 解析:连接AO,BO,CO.∵O是△ABC的角平分线的交点,∴三个小三角形的高相等(设高为x,),底边之和为4,. 解得x=1.
10. C 解析:如图,∵ ∠DEC=∠B+∠BDE, ∴x°+∠FEC=x°+∠BDE,∴∠FEC=∠BDE,∴其对应边应该是BE和CF,而已知给的是BD=FC=3,∴不能判定两个小三角形全等,故选 C.
11. C 解析:如图,延长AP交BC的延长线于E,由题意得∠APB = ∠BPE = 90°,∠ABP =∠EBP.由 ASA得△ABP≌△EBP,∴S△ABP=S△BEP,AP=PE,∴△APC 和△CPE等底同高, 设 △ACE 的 面 积 为 m,
12.1:4 解析:∵ ∠A:∠ABC:∠ACB=3:5:10,∴∠A=30°,∠ABC=50°,∠ACB=100°.∵△MNC≌△ABC,∴∠N=∠ABC=50°,∠M=∠A=30°,∴∠MCA=∠M+∠N=80°,∴∠BCM=20°,∠BCN=80°,∴∠BCM∶∠BCN=1∶4.
13.(0,-2)或(4,-2)或(4,2) 解析:点P的位置如图所示.
14.①②③④ 解析:∵ AD∥BC,∴∠ABC+∠BAD=180°.∵ AE,BE分别是∠BAD与∠ABC的平分线,∴ ∴∠AEB=180°-(∠BAE+∠ABE)=90°,故③正确.
延长AE交BC的延长线于F,如图,∵∠AEB=90°,∴BE⊥AF.∵ BE平分∠ABC,∴∠ABE=∠FBE.
∵∠ABE=∠FBE,BE=BE,∠AEB=∠FEB,∴ △ABE≌△FBE(ASA),∴AB=BF,AE=FE.∵ AD∥BC,∴∠EAD=∠F∴∠EAD=∠F,AE=FE,∠AED=∠FEC,∴△ADE≌△FCE(ASA),∴AD=CF,∴AB=BF=BC+CF=BC+AD,故①正确.∵ △ADE≌△FCE,∴DE=CE,
即点 E 为 CD 的中点,故②正确.∵ △ADE≌△FCE,∴ S△ADE = S四边形ABCD故④正确.
15.(1)如图,作A'F⊥BD,垂足为F.∵AC⊥BD,∴∠ACB=∠A'FB=90°,∴∠1+∠3=90°.又∵A'B⊥AB,∴∠1+∠2=90°,∴∠2=∠3.在△ACB 和△BFA'中, . △ACB≌△BFA'(AAS),∴A'F=BC.由题意 AC∥DE 且 CD⊥AC,AE⊥DE,∴CD=AE=1.8 m,∴BC=BD-CD=3-1.8=1.2(m),∴A'F=1.2m ,即A'到BD的距离是1.2m.
(2)由(1)知△ACB≌△BFA',∴BF=AC=2m.如图,作A'H⊥DE,垂足为H.∵A'F∥DE,∴A'H=FD,∴A'H=BD-BF=3-2=1(m),即A'到地面的距离是1m.
16.(1)如图,连接BD,CD.∵ DG⊥BC,BG=GC,∴由三角形全等可知DB=DC.∵ AD 平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF.在Rt△DEB和Rt△DFC 中, ∴ Rt△DEB≌Rt△DFC(HL),∴BE=CF.
(2)在 Rt△ADE 和Rt△ADF中, . Rt△ADE≌Rt△ADF(HL),∴AE=AF,∴AB-BE=AC+CF,∴2BE=AB-AC=16-10=6,∴BE=3.∴AE=AB-BE=16-3=13.
17. (1)120°.
(2)EF与DF之间的数量关系为EF=DF.理由:如图①,在AC 上截取 CG=CD,连接GF.∵CE是∠BCA的平分线,∴∠DCF=∠GCF.在△CFG 和△CFD中, ∴ △CFG ≌△CFD(SAS),∴GF=DF,∠CFD=∠CFG.∵ ∠B=60°,AD,CE分别是∠BAC,∠BCA 的平分线,∴ 且∠EAF=∠GAF,∴∠FAC+∠FCA= (∠BAC∠ACB) (180°-∠B)=60°,∴∠AFC=120°,∴∠CFD=60°∠CFG,∴ ∠AFG =60°.又∵ ∠AFE = ∠CFD=60°,∴ ∠AFE =∠AFG.在△AFE和△AFG中, ∴△AFE≌△AFG(ASA),∴EF=GF,∴DF=EF.
(3)AC=AE+CD.理由:如图②,在AC上截取 AG =AE,连接 GF.在 △EAF 和△GAF 中、△GAF(SAS),∴∠EFA=∠GFA.又由题可 A知, ∴∠AFC=180°-(∠FAC+∠FCA)= 120°,∴∠EFA=∠GFA=180°-120°=60°=∠DFC,∴∠CFG=∠CFD=60°.在△FDC 和△FGC中. . △FDC≌△FGC(ASA),∴CD=CG,∴AC=AG+CG=AE+CD.
