12.3 角的平分线的性质第2课时 角的平分线的判定同步练习 2024-2025学年人教版八年级数学上册(含答案)
文档属性
| 名称 | 12.3 角的平分线的性质第2课时 角的平分线的判定同步练习 2024-2025学年人教版八年级数学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 391.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 12:46:45 | ||
图片预览

文档简介
第2课时 角的平分线的判定
1.若△ABC内一点 O 到三角形三条边的距离相等,则O为△ABC ( )
A.角平分线的交点 B.高线的交点
C. 中线的交点 D.以上都不是
2.已知△ABC,两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB,AC上,且这组对应边所对的顶点重合于点M,点M一定在 ( )
A.∠A的平分线上 B. AC边的高上
C. BC边的中线上 D. AB 边的中线上
3.在正方形网格中,∠AOB 的位置如图所示,则点 P,Q,M,N中,在∠AOB的平分线上的是 点.
4.如图,已知点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠B 的平分线上;②在∠DAC的平分线上;③在∠ECA 的平分线上;④恰是∠B,∠DAC,∠ECA三个角的平分线的交点.上述结论中,正确结论有 .(填序号)
5.如图所示,为促进全民健身运动,某镇计划在张村与李村之间建一个娱乐健身场所.张村、李村坐落在两相交公路内,健身场所到两条公路的距离相等,并且到两村的距离和最短,请你通过作图确定健身场所的位置.
6.如图,P是OC上一点,PD⊥OA于D,PE⊥OB于E,F,G分别是OA,OB上的点,且PF=PG,DF=EG.求证:OC是∠AOB的平分线.
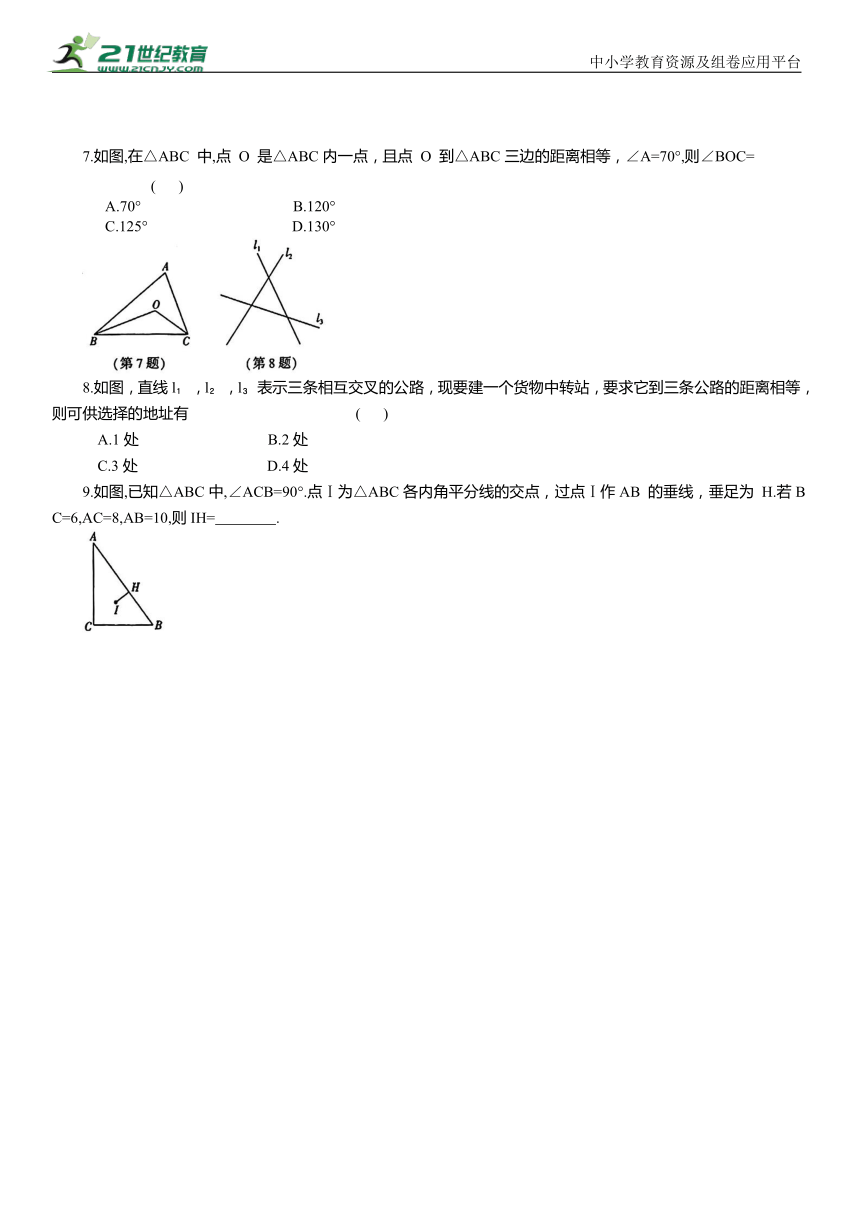
7.如图,在△ABC 中,点 O 是△ABC内一点,且点 O 到△ABC三边的距离相等,∠A=70°,则∠BOC= ( )
A.70° B.120°
C.125° D.130°
8.如图,直线l ,l ,l 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 ( )
A.1处 B.2处
C.3处 D.4处
9.如图,已知△ABC中,∠ACB=90°.点Ⅰ为△ABC各内角平分线的交点,过点Ⅰ作AB 的垂线,垂足为 H.若BC=6,AC=8,AB=10,则IH= .
中小学教育资源及组卷应用平台
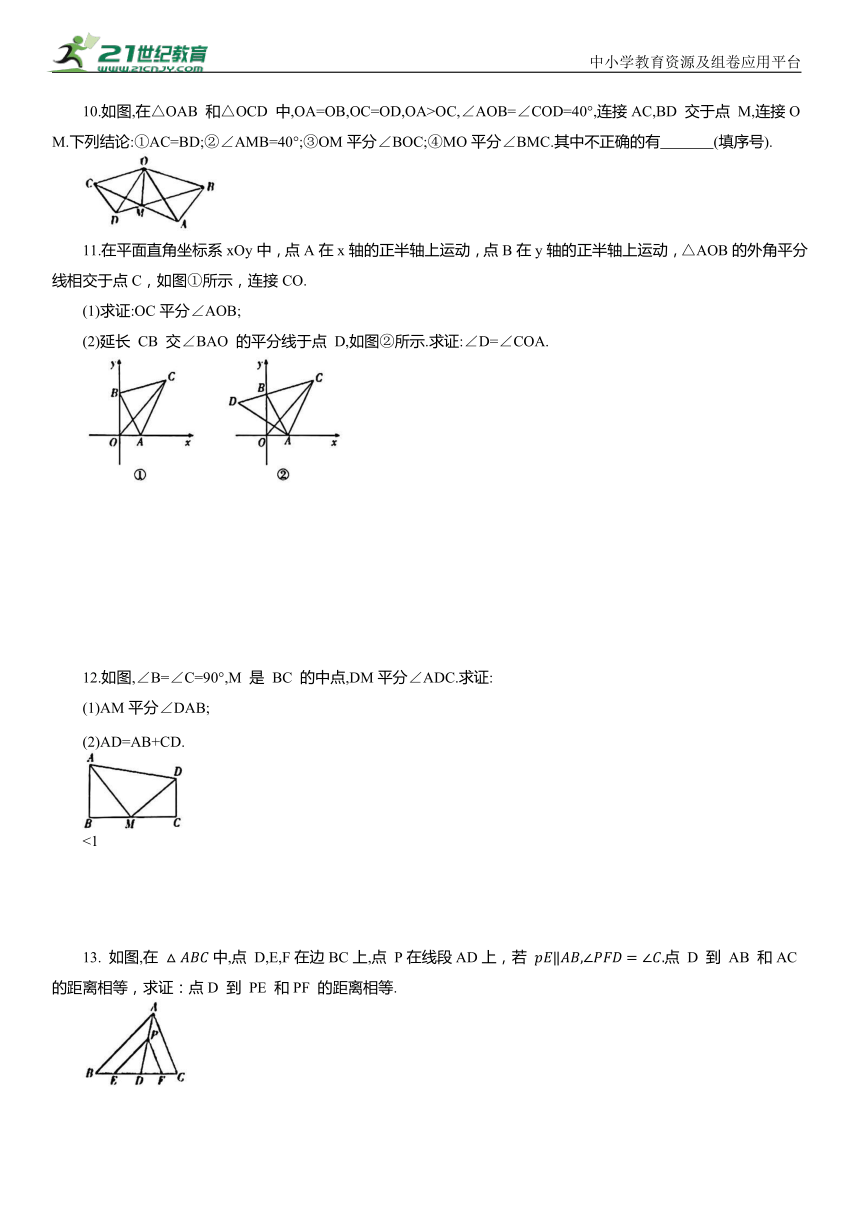
10.如图,在△OAB 和△OCD 中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD 交于点 M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中不正确的有 (填序号).
11.在平面直角坐标系xOy中,点A在x轴的正半轴上运动,点B在y轴的正半轴上运动,△AOB的外角平分线相交于点C,如图①所示,连接CO.
(1)求证:OC平分∠AOB;
(2)延长 CB 交∠BAO 的平分线于点 D,如图②所示.求证:∠D=∠COA.
12.如图,∠B=∠C=90°,M 是 BC 的中点,DM平分∠ADC.求证:
(1)AM平分∠DAB;
(2)AD=AB+CD.
<1
13. 如图,在 中,点 D,E,F在边BC上,点 P在线段AD上,若 点 D 到 AB 和AC的距离相等,求证:点D 到 PE 和PF 的距离相等.
14.如图,在△ABD中,∠BAD=80°,C 为BD延长线上一点,∠BAC=130°,△ABD 的角平分线 BE 与 AC交于点E,连接DE,求∠DEB的度数.
第2课时 角的平分线的判定
1. A 2. A 3. Q 4.①②③④
5.如图,连接EF,作∠ACB的平分线交EF 于点 O,则点 O 就是要建设健身场所的位置.
6. 在Rt△PFD 和Rt△PGE 中, Rt△PFD≌Rt△PGE(HL),∴PD=PE∵P是OC上一点,PD⊥OA,PE⊥OB,.. OC是∠AOB的平分线.
7. C
8. D 解析:如图.
9.2 解析:作IE⊥AC于E,IF⊥BC于F,连接IA,IB,IC.∵I为△ABC各内角平分线的交点,..IE=IF=IH,则 解得IH=2.
10. ③ 解析:由 SAS 证 明 △AOC≌ △BOD,得出 ∠OCA =∠ODB,AC=BD,①正确;由全等三角形的性质得出∠OAC=∠OBD,由三角形外角性质得∠AMB+∠OAC=∠AOB+∠OBD,得出∠AMB=∠AOB=40°,②正确;作 OG⊥MC 于 G,OH⊥MB于H,∠OGC=∠OHD=90°,由AAS证明△OCG≌△ODH,得出OG=OH,由角平分线的判定方法得出 MO平分∠BMC,④正确;由∠AOB=∠COD,得出当∠DOM=∠AOM时,OM才平分∠BOC,假设∠DOM=∠AOM, △AOC≌△BOD,∴ ∠COM=∠BOM,由MO平分∠BMC得出∠CMO=∠BMO,推出△COM≌△BOM(ASA),得OB=OC,∵OA=OB,∴OA=OC,而OA>OC,故③错误.
11.(1)如图①,过C分别向x轴、y轴、AB作垂线,垂足分别为H ,H ,H .∴ BC 平分∠ABH ,∴ CH = CH .. . AC 平分∠BAH ,∴CH =CH ,∴CH =CH ,.. OC平分∠AOB.
(2)如图②,延长AB 得到射线AE.∵ BC 为△AOB的外角平分线,∴∠1=∠ABC.∵∠EBD=∠ABC,∠OBD=∠1,∴∠EBD=∠OBD.∵AD平分∠BAO,∴∠OAD=∠BAD.∵ ∠OBE=∠AOB+∠BAO,∠DBE=∠BAD+∠D,且∠OBE =2∠DBE,∠BAO = ∴∠D=∠COA.
12.(1)过点M作ME⊥AD于E.∵∠B=∠C=90°,∴MB⊥AB,MC⊥CD.∵DM平分∠ADC,ME⊥AD,MC⊥CD,∴ME=MC.∵ M是BC的中点,∴MC=MB,∴MB=ME.又∵MB⊥AB,ME⊥AD,∴AM平分∠DAB.
(2)∵ME⊥AD,MC⊥CD,∴∠C=∠DEM=90°.在 Rt△DCM和Rt△DEM中, ∴ Rt△DCM≌Rt△DEM(HL), ∴ CD=DE,同理AE=AB.∵AE+DE=AD,∴AB+CD=AD.
13.如图,作DM⊥AB 于 M,交 PE 于 G,作 DN⊥AC 于 N,交 PF 于H.∵ DM=DN,DM⊥AB,DN⊥AC,∴∠BAD=∠CAD.∵ PE∥AB,∴∠EPD = ∠BAD,DG ⊥ PE.· ∠PFD = ∠C,.. PF ∥AC,∴∠FPD=∠CAD,DH⊥PF,..∠EPD=∠FPD,∴DG=DH,即点D到PE和PF的距离相等.
14.如图,过E作EF⊥AB交BA的延长线于F,EG⊥AD于G,EH⊥BC于 H.∵ BE 平分∠ABD,. E H=EF· ∠BAC=130°,∠BAD =80°,..∠FAE=∠CAD=50°,∴EF=EG,.. EG=EH,.. DE平分∠CDG,..∠HED=∠DEG.设∠DEG=y°,∠GEB=x°,∵∠EFA=∠EGA=90°,∴∠GEA=∠FEA =40°.∵ ∠EFB= ∠EHB =90°,∠EBF=∠EBH,∴∠FEB=∠HEB,..2y+x=80-x,.. y+x=40,即∠DEB=40°.
1.若△ABC内一点 O 到三角形三条边的距离相等,则O为△ABC ( )
A.角平分线的交点 B.高线的交点
C. 中线的交点 D.以上都不是
2.已知△ABC,两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB,AC上,且这组对应边所对的顶点重合于点M,点M一定在 ( )
A.∠A的平分线上 B. AC边的高上
C. BC边的中线上 D. AB 边的中线上
3.在正方形网格中,∠AOB 的位置如图所示,则点 P,Q,M,N中,在∠AOB的平分线上的是 点.
4.如图,已知点P到BE,BD,AC的距离恰好相等,则点P的位置:①在∠B 的平分线上;②在∠DAC的平分线上;③在∠ECA 的平分线上;④恰是∠B,∠DAC,∠ECA三个角的平分线的交点.上述结论中,正确结论有 .(填序号)
5.如图所示,为促进全民健身运动,某镇计划在张村与李村之间建一个娱乐健身场所.张村、李村坐落在两相交公路内,健身场所到两条公路的距离相等,并且到两村的距离和最短,请你通过作图确定健身场所的位置.
6.如图,P是OC上一点,PD⊥OA于D,PE⊥OB于E,F,G分别是OA,OB上的点,且PF=PG,DF=EG.求证:OC是∠AOB的平分线.
7.如图,在△ABC 中,点 O 是△ABC内一点,且点 O 到△ABC三边的距离相等,∠A=70°,则∠BOC= ( )
A.70° B.120°
C.125° D.130°
8.如图,直线l ,l ,l 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有 ( )
A.1处 B.2处
C.3处 D.4处
9.如图,已知△ABC中,∠ACB=90°.点Ⅰ为△ABC各内角平分线的交点,过点Ⅰ作AB 的垂线,垂足为 H.若BC=6,AC=8,AB=10,则IH= .
中小学教育资源及组卷应用平台
10.如图,在△OAB 和△OCD 中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD 交于点 M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中不正确的有 (填序号).
11.在平面直角坐标系xOy中,点A在x轴的正半轴上运动,点B在y轴的正半轴上运动,△AOB的外角平分线相交于点C,如图①所示,连接CO.
(1)求证:OC平分∠AOB;
(2)延长 CB 交∠BAO 的平分线于点 D,如图②所示.求证:∠D=∠COA.
12.如图,∠B=∠C=90°,M 是 BC 的中点,DM平分∠ADC.求证:
(1)AM平分∠DAB;
(2)AD=AB+CD.
<1
13. 如图,在 中,点 D,E,F在边BC上,点 P在线段AD上,若 点 D 到 AB 和AC的距离相等,求证:点D 到 PE 和PF 的距离相等.
14.如图,在△ABD中,∠BAD=80°,C 为BD延长线上一点,∠BAC=130°,△ABD 的角平分线 BE 与 AC交于点E,连接DE,求∠DEB的度数.
第2课时 角的平分线的判定
1. A 2. A 3. Q 4.①②③④
5.如图,连接EF,作∠ACB的平分线交EF 于点 O,则点 O 就是要建设健身场所的位置.
6. 在Rt△PFD 和Rt△PGE 中, Rt△PFD≌Rt△PGE(HL),∴PD=PE∵P是OC上一点,PD⊥OA,PE⊥OB,.. OC是∠AOB的平分线.
7. C
8. D 解析:如图.
9.2 解析:作IE⊥AC于E,IF⊥BC于F,连接IA,IB,IC.∵I为△ABC各内角平分线的交点,..IE=IF=IH,则 解得IH=2.
10. ③ 解析:由 SAS 证 明 △AOC≌ △BOD,得出 ∠OCA =∠ODB,AC=BD,①正确;由全等三角形的性质得出∠OAC=∠OBD,由三角形外角性质得∠AMB+∠OAC=∠AOB+∠OBD,得出∠AMB=∠AOB=40°,②正确;作 OG⊥MC 于 G,OH⊥MB于H,∠OGC=∠OHD=90°,由AAS证明△OCG≌△ODH,得出OG=OH,由角平分线的判定方法得出 MO平分∠BMC,④正确;由∠AOB=∠COD,得出当∠DOM=∠AOM时,OM才平分∠BOC,假设∠DOM=∠AOM, △AOC≌△BOD,∴ ∠COM=∠BOM,由MO平分∠BMC得出∠CMO=∠BMO,推出△COM≌△BOM(ASA),得OB=OC,∵OA=OB,∴OA=OC,而OA>OC,故③错误.
11.(1)如图①,过C分别向x轴、y轴、AB作垂线,垂足分别为H ,H ,H .∴ BC 平分∠ABH ,∴ CH = CH .. . AC 平分∠BAH ,∴CH =CH ,∴CH =CH ,.. OC平分∠AOB.
(2)如图②,延长AB 得到射线AE.∵ BC 为△AOB的外角平分线,∴∠1=∠ABC.∵∠EBD=∠ABC,∠OBD=∠1,∴∠EBD=∠OBD.∵AD平分∠BAO,∴∠OAD=∠BAD.∵ ∠OBE=∠AOB+∠BAO,∠DBE=∠BAD+∠D,且∠OBE =2∠DBE,∠BAO = ∴∠D=∠COA.
12.(1)过点M作ME⊥AD于E.∵∠B=∠C=90°,∴MB⊥AB,MC⊥CD.∵DM平分∠ADC,ME⊥AD,MC⊥CD,∴ME=MC.∵ M是BC的中点,∴MC=MB,∴MB=ME.又∵MB⊥AB,ME⊥AD,∴AM平分∠DAB.
(2)∵ME⊥AD,MC⊥CD,∴∠C=∠DEM=90°.在 Rt△DCM和Rt△DEM中, ∴ Rt△DCM≌Rt△DEM(HL), ∴ CD=DE,同理AE=AB.∵AE+DE=AD,∴AB+CD=AD.
13.如图,作DM⊥AB 于 M,交 PE 于 G,作 DN⊥AC 于 N,交 PF 于H.∵ DM=DN,DM⊥AB,DN⊥AC,∴∠BAD=∠CAD.∵ PE∥AB,∴∠EPD = ∠BAD,DG ⊥ PE.· ∠PFD = ∠C,.. PF ∥AC,∴∠FPD=∠CAD,DH⊥PF,..∠EPD=∠FPD,∴DG=DH,即点D到PE和PF的距离相等.
14.如图,过E作EF⊥AB交BA的延长线于F,EG⊥AD于G,EH⊥BC于 H.∵ BE 平分∠ABD,. E H=EF· ∠BAC=130°,∠BAD =80°,..∠FAE=∠CAD=50°,∴EF=EG,.. EG=EH,.. DE平分∠CDG,..∠HED=∠DEG.设∠DEG=y°,∠GEB=x°,∵∠EFA=∠EGA=90°,∴∠GEA=∠FEA =40°.∵ ∠EFB= ∠EHB =90°,∠EBF=∠EBH,∴∠FEB=∠HEB,..2y+x=80-x,.. y+x=40,即∠DEB=40°.
