第十二章全等三角形提优测试卷 2024-2025学年人教版八年级数学上册(含答案)
文档属性
| 名称 | 第十二章全等三角形提优测试卷 2024-2025学年人教版八年级数学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 548.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 12:57:18 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十二章全等三角形提优测试卷
(时间:90分钟 满分:100分)
一、选择题(每小题4分,共32分)
1. 下列条件中能作出唯一的三角形的是 ( )
A.已知两边及一边的对角
B.已知两角
C. 已知两边及第三边上的高线
D.已知两边及第三边上的中线
2.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①②③④),若要配一块与原来大小一样的三角形玻璃,应该带 ( )
A.第①块 B.第②块
C.第③块 D.第④块
3.如图,在四边形ABCD中,AB=CD,BA 和CD的延长线交于点 E,若点 P 使得 则满足此条件的点 P ( )
A.有且只有1个
B.有且只有2个
C.组成∠E的平分线
D.组成∠E的平分线所在的直线(点E除外)
4.如图,点 D,E分别在线段AB,AC上,CD与BE相交于 O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD ( )
A.∠B=∠C B. AD=AE
C. BD=CE D. BE=CD
5.长为l的一根绳,恰好可以围成两个全等三角形,则其中一个三角形的最长边x的取值范围是 ( )
6.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究
筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=2AC·BD.其中正确的结论有 ( )
A.0个 B.1个 C.2个 D.3个
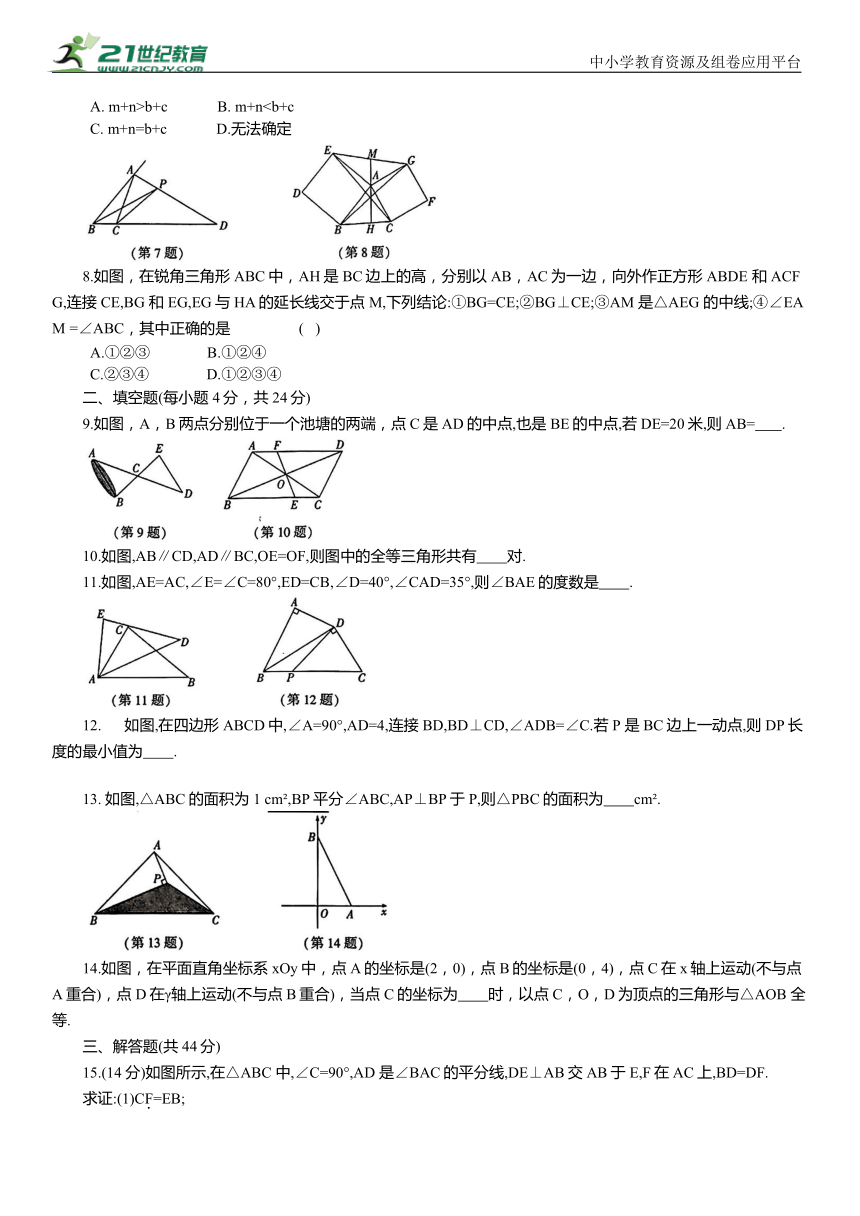
7.如图,在△ABC中,AD是△BAC的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则m+n与b+c的大小关系是 ( )
A. m+n>b+c B. m+nC. m+n=b+c D.无法确定
8.如图,在锐角三角形ABC中,AH是BC边上的高,分别以AB,AC为一边,向外作正方形 ABDE 和 ACFG,连接CE,BG 和 EG,EG与HA的延长线交于点 M,下列结论:①BG=CE;②BG⊥CE;③AM 是△AEG 的中线;④∠EAM =∠ABC,其中正确的是 ( )
A.①②③ B.①②④
C.②③④ D.①②③④
二、填空题(每小题4分,共24分)
9.如图,A,B两点分别位于一个池塘的两端,点C是AD的中点,也是BE的中点,若DE=20米,则AB= .
10.如图,AB∥CD,AD∥BC,OE=OF,则图中的全等三角形共有 对.
11.如图,AE=AC,∠E=∠C=80°,ED=CB,∠D=40°,∠CAD=35°,则∠BAE的度数是 .
如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P 是BC边上一动点,则 DP长度的最小值为 .
13. 如图,△ABC的面积为 1 cm ,BP平分∠ABC,AP⊥BP于P,则△PBC的面积为 cm .
14.如图,在平面直角坐标系xOy中,点A的坐标是(2,0),点B的坐标是(0,4),点C在x轴上运动(不与点A重合),点D在γ轴上运动(不与点B重合),当点C的坐标为 时,以点C,O,D为顶点的三角形与△AOB 全等.
三、解答题(共44分)
15.(14 分)如图所示,在△ABC 中,∠C=90°,AD 是∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF.
求证:(1)CF=EB;
(2)AB=AF+2EB.
16.(14分)如图①所示,BD,CE是△ABC 的高,点 P 在 BD 的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)探究AP与AQ 之间的关系.
(2)如图②,若把(1)中的△ABC改为钝角三角形,AC>AB,∠A 是钝角,其他条件不变,上述结论是否成立 画出图形并证明你的结论.
17.(16分)问题背景:
(1)如图①,在四边形ABCD 中,AB=AD,∠BAD=120°,∠B=∠ADC=90°. E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,DF之间的数量关系.小王同学探究此问题的方法是延长 FD到点 G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 .
探索延伸:
(2)如图②,若在四边形 ABCD 中,AB=AD,∠B+∠D=180°. E,F 分别是BC,CD 上的点,且 上述结论是否仍然成立 并说明理由.
实际应用:
(3)如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进.2小时后,甲、乙两舰艇分别到达E,F处,此时在指挥中心观测到两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
1. D 2. B 3. D 4. D 5. A 6. C
7. A 解析:如图,在BA的延长线上取点 E,使AE=AC,连接EP.
∵ AD是△BAC 的外角平分线,∴∠CAD=∠EAD.由 SAS可证得△ACP≌△AEP,∴PE=PC.在△PBE中,PB+PE>AB+AE.∵PB=m,PC=n,AB=c,AC=b,∴m+n>b+c.
8. D 解析:在正方形 ABDE和ACFG中,AB=AE,AC=AG,∠BAE=∠CAG=90°,∴ ∠BAE +∠BAC = ∠CAG+∠BAC,即 ∠CAE =
∠BAC. (ECAE,∠CAB,∴△ABC≌△ABC(SAS),∴BC=CE,B
①正确;设 BG,CE 相交于点 N,∵ △ABG≌△AEC,∴ ∠ACE=∠AGB. ∵ ∠NCF+∠NGF=∠ACF+∠AGF=180°,∴∠CNG=360°- 故②正确;过点E作EP⊥HA交HA的延长线于P,过点G作GQ⊥AM于Q,∴AH⊥BC,. ∠ABH+∠BAH=90°.∵ ∠BAE=90°,∴∠EAP+∠BAH = 180°- 90°= 90°, ∴ ∠ABH = ∠EAP, 故 ④ 正确;
,(△BE⊥∠EASOD,∴△BB≌△BP(△AS),∴BP≌4.5=18
可得00:46,∴EP=00.(LEMMNCGOD,∴△EM≌△GQM(AAS),∴EM=GM,.. AM是△AEG的中线,故③正确.综上所述,①②③④都正确.
9.20米 10.6 11.85°
12.4 解析:当DP⊥BC时,DP的长度最小.∵BD⊥CD,即∠BDC=90°.又∠A = 90°,∴ ∠A =∠BDC.又∠ADB =∠C,∴∠ABD=∠CBD.又DA⊥BA,DP⊥BC,.. AD=DP.又AD=4,.. DP=4.
13.0.5 解析:如图,延长 AP 交 BC 于E.∵ BP 平 分 ∠ABC, ∴∠ABP=∠EBP.∵ AP ⊥ BP,. . ∠APB =∠EPB=90°.在△ABP 和△EBP 中,
. △ABP ≌ △EBP
(ASA),∴AP=PE,.. S△ABP=S△EBP,S△ACP=S△ECP,.. S△PBC=
14.(-4,0)或(-2,0)或(4,0) 解析:如图①所示,当点C在x轴负半轴上,点 D在y轴负半轴上时,△AOB≌△COD,. . CO=AO=2,∴C(-2,0);
如图②所示,当点C在x轴负半轴上,点D在y轴上时,△AOB≌△DOC,∴CO=BO=4,∴C(-4,0);
如图③所示,当点 C 在 x 轴的正半轴上,点D 在 y 轴上时,△AOB≌△DOC,∴CO=BO=4,∴C(4,0).
15.(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,∴DE=DC.在Rt△CDF和 Rt△EDB 中, ∴ Rt△CDF≌Rt△EDB(HL),∴CF=EB.
(2)在Rt△ACD与Rt△AED中 Rt△ACD≌Rt△AED(HL),.. AC=AE,∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
16.(1)∵ BD,CE是△ABC的高,∴∠1+∠CAB=90°,∠2+∠CAB=90°,∴∠1=∠2. 在△QAC和△APB 中,101422.∴△QC≌△APB(SAS),∴ AQ=AP,∠QAC=∠P.而∠DAP+∠P =90°,∴∠DAP+∠QAC=90°,即∠QAP=90°,∴AQ⊥AP.即AP=AQ,AP⊥AQ.(2)上述结论成立,证明如下:如图所示:∵BD,CE是△ABC的高,∴∠1+∠CAE = 90°, ∠2 + ∠DAB = 90°.∵∠CAE = ∠DAB,∴∠1 = ∠2. 在△QAC 和 △APB 中, ∴△QAC≌△APB(SAS),∴AQ=AP,∠QAC=∠P.∵ ∠PDA =90°,∴ ∠P+∠PAD=90°,∴ ∠QAC+∠PAD=90°,∴∠QAP=90°,∴AQ⊥AP.即AP=AQ,AP⊥AQ.
17.(1)EF=BE+DF 解析:∵在△ABE和△ADG中 ∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG.∵ ∠EAF= ∠BAD=60°,∴∠GAF =∠DAG+∠DAF =∠BAE+∠DAF ∠BAD-∠EAF=60°,∴∠EAF=∠GAF.在△AEF 和△AGF中,(是否则∠CAF,∴△AB≌△ECE≌∠CAE;△AFCDACF中,∴BP≌△P中,
DG+DF=BE+DF,∴EF=BE+DF.
(2)结论EF=BE+DF 仍然成立.理由如下:延长 FD 到点 G,使DG=BE,连接AG∴∠B+∠ADC=180°,∠ADC+∠ADG=180°,∴∠B=∠ADG.在△ABE和△ADG中,(BBB2ADC...△AB≌≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG.∵ ∠EAF ∠BAD∴∠GAF= ∠DAG +∠DAF = ∠BAE + ∠DAF = ∠BAD - ∠EAF =∠EAF, ∴ ∠EAF = ∠GAF. 在 △AEF 和 △AGF 中,
(LEAGC,CGAF,∴ △ABCD,∴EF=△AF(BAB)... EF=△CF中,
DG+DF=BE+DF,. EF=BE+DF.
连接EF,延长AE,BF相交于点(C.∴ 又∵ OA=OB, ∴符合探索延伸中的条件,∴结论EF=AE+BF成立,即EF=2×(60+80)=280(海里).答:此时两舰艇之间的距离是280海里.
第十二章全等三角形提优测试卷
(时间:90分钟 满分:100分)
一、选择题(每小题4分,共32分)
1. 下列条件中能作出唯一的三角形的是 ( )
A.已知两边及一边的对角
B.已知两角
C. 已知两边及第三边上的高线
D.已知两边及第三边上的中线
2.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①②③④),若要配一块与原来大小一样的三角形玻璃,应该带 ( )
A.第①块 B.第②块
C.第③块 D.第④块
3.如图,在四边形ABCD中,AB=CD,BA 和CD的延长线交于点 E,若点 P 使得 则满足此条件的点 P ( )
A.有且只有1个
B.有且只有2个
C.组成∠E的平分线
D.组成∠E的平分线所在的直线(点E除外)
4.如图,点 D,E分别在线段AB,AC上,CD与BE相交于 O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD ( )
A.∠B=∠C B. AD=AE
C. BD=CE D. BE=CD
5.长为l的一根绳,恰好可以围成两个全等三角形,则其中一个三角形的最长边x的取值范围是 ( )
6.两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究
筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=2AC·BD.其中正确的结论有 ( )
A.0个 B.1个 C.2个 D.3个
7.如图,在△ABC中,AD是△BAC的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则m+n与b+c的大小关系是 ( )
A. m+n>b+c B. m+n
8.如图,在锐角三角形ABC中,AH是BC边上的高,分别以AB,AC为一边,向外作正方形 ABDE 和 ACFG,连接CE,BG 和 EG,EG与HA的延长线交于点 M,下列结论:①BG=CE;②BG⊥CE;③AM 是△AEG 的中线;④∠EAM =∠ABC,其中正确的是 ( )
A.①②③ B.①②④
C.②③④ D.①②③④
二、填空题(每小题4分,共24分)
9.如图,A,B两点分别位于一个池塘的两端,点C是AD的中点,也是BE的中点,若DE=20米,则AB= .
10.如图,AB∥CD,AD∥BC,OE=OF,则图中的全等三角形共有 对.
11.如图,AE=AC,∠E=∠C=80°,ED=CB,∠D=40°,∠CAD=35°,则∠BAE的度数是 .
如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P 是BC边上一动点,则 DP长度的最小值为 .
13. 如图,△ABC的面积为 1 cm ,BP平分∠ABC,AP⊥BP于P,则△PBC的面积为 cm .
14.如图,在平面直角坐标系xOy中,点A的坐标是(2,0),点B的坐标是(0,4),点C在x轴上运动(不与点A重合),点D在γ轴上运动(不与点B重合),当点C的坐标为 时,以点C,O,D为顶点的三角形与△AOB 全等.
三、解答题(共44分)
15.(14 分)如图所示,在△ABC 中,∠C=90°,AD 是∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF.
求证:(1)CF=EB;
(2)AB=AF+2EB.
16.(14分)如图①所示,BD,CE是△ABC 的高,点 P 在 BD 的延长线上,CA=BP,点Q在CE上,QC=AB.
(1)探究AP与AQ 之间的关系.
(2)如图②,若把(1)中的△ABC改为钝角三角形,AC>AB,∠A 是钝角,其他条件不变,上述结论是否成立 画出图形并证明你的结论.
17.(16分)问题背景:
(1)如图①,在四边形ABCD 中,AB=AD,∠BAD=120°,∠B=∠ADC=90°. E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,DF之间的数量关系.小王同学探究此问题的方法是延长 FD到点 G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 .
探索延伸:
(2)如图②,若在四边形 ABCD 中,AB=AD,∠B+∠D=180°. E,F 分别是BC,CD 上的点,且 上述结论是否仍然成立 并说明理由.
实际应用:
(3)如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进.2小时后,甲、乙两舰艇分别到达E,F处,此时在指挥中心观测到两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
1. D 2. B 3. D 4. D 5. A 6. C
7. A 解析:如图,在BA的延长线上取点 E,使AE=AC,连接EP.
∵ AD是△BAC 的外角平分线,∴∠CAD=∠EAD.由 SAS可证得△ACP≌△AEP,∴PE=PC.在△PBE中,PB+PE>AB+AE.∵PB=m,PC=n,AB=c,AC=b,∴m+n>b+c.
8. D 解析:在正方形 ABDE和ACFG中,AB=AE,AC=AG,∠BAE=∠CAG=90°,∴ ∠BAE +∠BAC = ∠CAG+∠BAC,即 ∠CAE =
∠BAC. (ECAE,∠CAB,∴△ABC≌△ABC(SAS),∴BC=CE,B
①正确;设 BG,CE 相交于点 N,∵ △ABG≌△AEC,∴ ∠ACE=∠AGB. ∵ ∠NCF+∠NGF=∠ACF+∠AGF=180°,∴∠CNG=360°- 故②正确;过点E作EP⊥HA交HA的延长线于P,过点G作GQ⊥AM于Q,∴AH⊥BC,. ∠ABH+∠BAH=90°.∵ ∠BAE=90°,∴∠EAP+∠BAH = 180°- 90°= 90°, ∴ ∠ABH = ∠EAP, 故 ④ 正确;
,(△BE⊥∠EASOD,∴△BB≌△BP(△AS),∴BP≌4.5=18
可得00:46,∴EP=00.(LEMMNCGOD,∴△EM≌△GQM(AAS),∴EM=GM,.. AM是△AEG的中线,故③正确.综上所述,①②③④都正确.
9.20米 10.6 11.85°
12.4 解析:当DP⊥BC时,DP的长度最小.∵BD⊥CD,即∠BDC=90°.又∠A = 90°,∴ ∠A =∠BDC.又∠ADB =∠C,∴∠ABD=∠CBD.又DA⊥BA,DP⊥BC,.. AD=DP.又AD=4,.. DP=4.
13.0.5 解析:如图,延长 AP 交 BC 于E.∵ BP 平 分 ∠ABC, ∴∠ABP=∠EBP.∵ AP ⊥ BP,. . ∠APB =∠EPB=90°.在△ABP 和△EBP 中,
. △ABP ≌ △EBP
(ASA),∴AP=PE,.. S△ABP=S△EBP,S△ACP=S△ECP,.. S△PBC=
14.(-4,0)或(-2,0)或(4,0) 解析:如图①所示,当点C在x轴负半轴上,点 D在y轴负半轴上时,△AOB≌△COD,. . CO=AO=2,∴C(-2,0);
如图②所示,当点C在x轴负半轴上,点D在y轴上时,△AOB≌△DOC,∴CO=BO=4,∴C(-4,0);
如图③所示,当点 C 在 x 轴的正半轴上,点D 在 y 轴上时,△AOB≌△DOC,∴CO=BO=4,∴C(4,0).
15.(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,∴DE=DC.在Rt△CDF和 Rt△EDB 中, ∴ Rt△CDF≌Rt△EDB(HL),∴CF=EB.
(2)在Rt△ACD与Rt△AED中 Rt△ACD≌Rt△AED(HL),.. AC=AE,∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.
16.(1)∵ BD,CE是△ABC的高,∴∠1+∠CAB=90°,∠2+∠CAB=90°,∴∠1=∠2. 在△QAC和△APB 中,101422.∴△QC≌△APB(SAS),∴ AQ=AP,∠QAC=∠P.而∠DAP+∠P =90°,∴∠DAP+∠QAC=90°,即∠QAP=90°,∴AQ⊥AP.即AP=AQ,AP⊥AQ.(2)上述结论成立,证明如下:如图所示:∵BD,CE是△ABC的高,∴∠1+∠CAE = 90°, ∠2 + ∠DAB = 90°.∵∠CAE = ∠DAB,∴∠1 = ∠2. 在△QAC 和 △APB 中, ∴△QAC≌△APB(SAS),∴AQ=AP,∠QAC=∠P.∵ ∠PDA =90°,∴ ∠P+∠PAD=90°,∴ ∠QAC+∠PAD=90°,∴∠QAP=90°,∴AQ⊥AP.即AP=AQ,AP⊥AQ.
17.(1)EF=BE+DF 解析:∵在△ABE和△ADG中 ∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG.∵ ∠EAF= ∠BAD=60°,∴∠GAF =∠DAG+∠DAF =∠BAE+∠DAF ∠BAD-∠EAF=60°,∴∠EAF=∠GAF.在△AEF 和△AGF中,(是否则∠CAF,∴△AB≌△ECE≌∠CAE;△AFCDACF中,∴BP≌△P中,
DG+DF=BE+DF,∴EF=BE+DF.
(2)结论EF=BE+DF 仍然成立.理由如下:延长 FD 到点 G,使DG=BE,连接AG∴∠B+∠ADC=180°,∠ADC+∠ADG=180°,∴∠B=∠ADG.在△ABE和△ADG中,(BBB2ADC...△AB≌≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG.∵ ∠EAF ∠BAD∴∠GAF= ∠DAG +∠DAF = ∠BAE + ∠DAF = ∠BAD - ∠EAF =∠EAF, ∴ ∠EAF = ∠GAF. 在 △AEF 和 △AGF 中,
(LEAGC,CGAF,∴ △ABCD,∴EF=△AF(BAB)... EF=△CF中,
DG+DF=BE+DF,. EF=BE+DF.
连接EF,延长AE,BF相交于点(C.∴ 又∵ OA=OB, ∴符合探索延伸中的条件,∴结论EF=AE+BF成立,即EF=2×(60+80)=280(海里).答:此时两舰艇之间的距离是280海里.
