12.2 三角形全等的判定第3课时 三角形全等的判定(3)“ASA”与“AAS” 同步练习 2024-2025学年人教版八年级数学上册(含答案)
文档属性
| 名称 | 12.2 三角形全等的判定第3课时 三角形全等的判定(3)“ASA”与“AAS” 同步练习 2024-2025学年人教版八年级数学上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 466.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 12:50:48 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第3课时 三角形全等的判定(3)“ASA”与“AAS”
1.如图,小周书上的三角形被墨迹污染了一部分,他根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是 ( )
A. SSS B. SAS C. AAS D. ASA
2.如图,已知AB=AC,点D,E分别在线段AB,AC上,BE与CD相交于点O,添加以下哪个条件仍不能判定△ABE≌△ACD ( )
A.∠B=∠C B.∠AEB=∠ADC
C. BD=CE D. BE=CD
3.如图,已知∠ACD=∠BCE,AC=DC,当添加条件 时,可依据“ASA”证明△ACB≌△DCE;当添加条件 时,可依据“AAS”证明△ACB≌△DCE. (不添加辅助线和字母)
4.如图,AB∥CF,E为DF的中点,若AB=9cm,CF=6cm,则BD= cm.
5.已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
6.如图,在△ABC中,∠B=∠C,D是BA延长线上一点,E是AC的中点,连接DE并延长,交BC于点M,∠DAC的平分线交DM于点F.求证:AF=CM.
7.如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=AE.其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
8如图,AB⊥CD,且AB=CD. E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为 ( )
A. a+c B. b+c C. a-b+c D. a+b-c
9.如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-8,3),点B的坐标是 ( )
A.(2,6) B.(1,6) C.(3,8) D.(1,8)
10.如图,AB=10,∠A=∠B=45°,AC=BD= .点E,为线段AB上两点.现存在以下条件:①CE=DF=4;②AF=BE;③∠CEB=∠DFA;④CE=DF=5.请在以上条件中选择一个条件,使得△ACE一定和△BDF全等,则这个条件可以为 .(写出所有正确答案的序号)
11.如图,Rt△ABC中,∠C=90°,E为AB的中点,D为AC上一点,BF∥AC交DE的延长线于点F. AC=6,BF与AC之间的距离为5,则四边形 FBCD 周长的最小值是 .
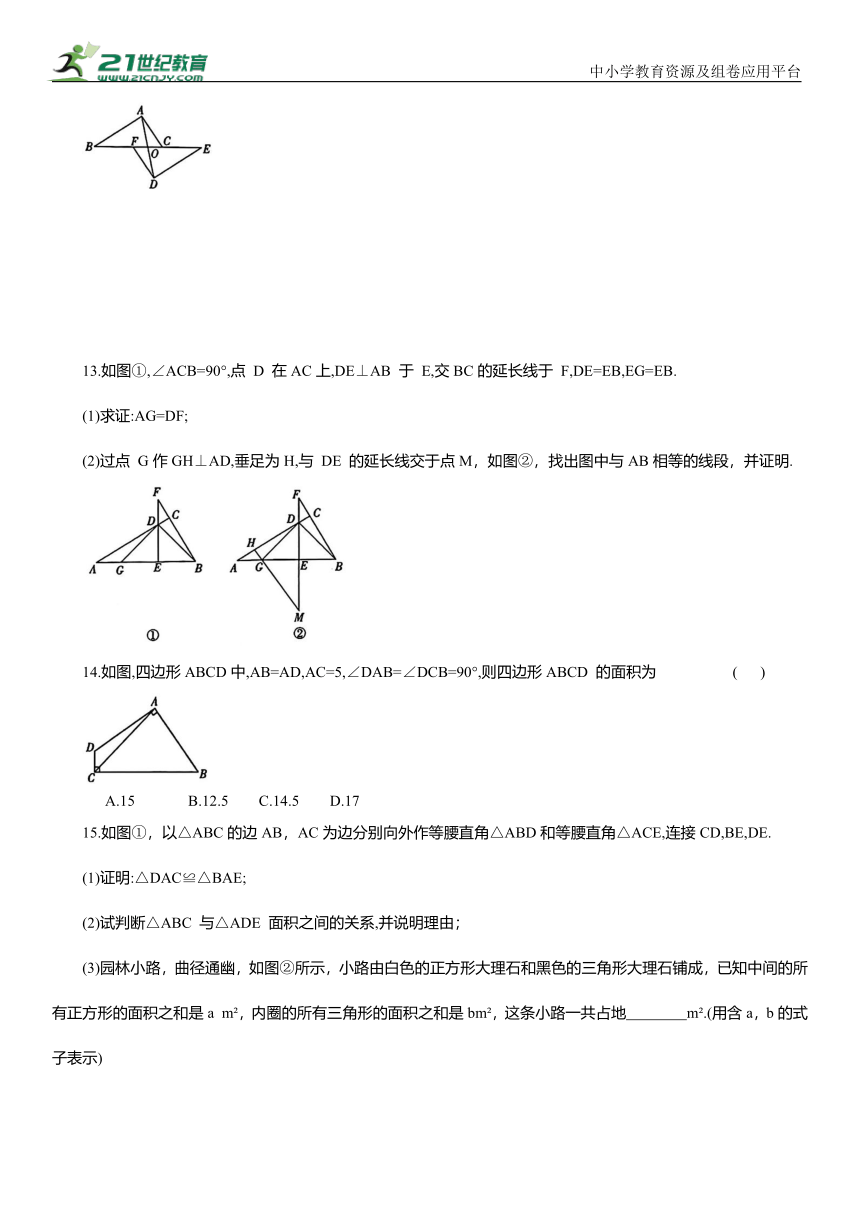
12.如图,点B,F,C,E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.求证:AD与BE互相平分.
13.如图①,∠ACB=90°,点 D 在AC上,DE⊥AB 于 E,交BC的延长线于 F,DE=EB,EG=EB.
(1)求证:AG=DF;
(2)过点 G作GH⊥AD,垂足为H,与 DE 的延长线交于点M,如图②,找出图中与AB相等的线段,并证明.
14.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD 的面积为 ( )
A.15 B.12.5 C.14.5 D.17
15.如图①,以△ABC的边AB,AC为边分别向外作等腰直角△ABD和等腰直角△ACE,连接CD,BE,DE.
(1)证明:△DAC≌△BAE;
(2)试判断△ABC 与△ADE 面积之间的关系,并说明理由;
(3)园林小路,曲径通幽,如图②所示,小路由白色的正方形大理石和黑色的三角形大理石铺成,已知中间的所有正方形的面积之和是a m ,内圈的所有三角形的面积之和是bm ,这条小路一共占地 m .(用含a,b的式子表示)
第3课时 三角形全等的判定(3)“ASA”与“AAS”1. D 2. D 3.∠A=∠D ∠B=∠E 4.3
5. 由∠ECB=70°得∠ACB=110°,又∵ ∠D=110°,∴ ∠ACB=∠D.∵AB∥DE,∴ ∠CAB=∠E.在△ABC 和△EAD 中, ∴△ABC≌△EAD(AAS).
6.∵ ∠B=∠C,. ∠DAC=∠B+∠C=2∠C.∵ AF是∠DAC的平分线, E 是 AC的中点,∴AE=CE. 在△AEF和△CEM中 .△AEF≌△CEM(ASA),.. AF=CM.
7. C 解析:根据三角形的内角和定理求出∠EAB=∠FAC,进而得出∠1=∠2,∴ ①正确;根据 AAS 证明△EAB≌△FAC,∴BE=CF,AB=AC,∴②正确;根据 ASA 证明△ACN≌△ABM,∴③正确;..根据已知不能推出CD=AE,∴④错误.
8. D 解析:∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠AFB=∠CED=90°,∴∠A+∠D=90°,∠C+∠D=90°,∴∠A=∠C.∵ AB=CD,∴△ABF≌△CDE(AAS),.. AF=CE=a,BF=DE=b.∵ EF=c,.. AD=AF+DF=a+(b-c)=a+b-c.
9. B 解析:如图,过点 A 和点 B分别作AD⊥OC 于 D,BE⊥OC 于 E,∴∠ACD+∠CAD =90°,∠ACD + ∠BCE = 90°, ∴ ∠CAD =∠BCE. ∵ ∠ADC = ∠CEB, ∠CAD =∠BCE, AC = BC, . △ADC ≌ △CEB(AAS),∴DC=BE,AD=CE.:点C(-2,0),点A(-8,3),∴OC=2,AD=CE=3,OD=8,∴ CD=OD-OC=6,OE=CE-OC=1,∴BE=DC=6,∴点B的坐标是(1,6).
10.②③④ 解析:②可用SAS判定.③可用AAS判定.∴ 点E,F在线段AB上,4<3√2<5,∴当CE=4时,点E的位置有两个;当CE=5时,点E的位置只有一个,①不可以,④可以.
11.16 解析:∵ E 为AB 的中点,∴BE=AE.∵ BF∥AC,∴∠EBF=∠EAD.在 △BFE 和 △ADE 中, ∴ △BFE≌△ADE(ASA),∴BF=AD.∴四边形FBCD的周长=BF+FD+CD+BC=AD+CD+FD+BC=AC+BC+FD=11+FD.当FD⊥AC时,FD最短,此时FD=5,∴四边形FBCD周长的最小值为5+11=16.
12. ∵FB=CE,∴BC=EF.又∵AB∥ED,AC∥FD,∴∠ABC=∠DEF,∠ACB = ∠DFE. 在 △ABC 和 △DEF 中, ∴△ABC≌△DEF(ASA),∴ AC=DF.在△AOC 和△DOF 中,(20022000.050,∴AO=DOF中,∴AO=DOF中,COFO △DOF(AAS),∴AO=DOF中,DO=
CO.∵BF=CE,∴BO=EO,∴AD与BE互相平分.
13.(1)∵ DE⊥AB,..∠DEG=∠DEB=90°.又 DE=DE,EG=EB,∴△DEG≌△DEB(SAS),.. DG=DB,∠DGB=∠DBG.取GD中点P,连接 EP, 在 △EDP 和 △EGP 中, . . △EDP≌△EGP,∴∠EGD =∠EDG.又∠DEG=90°,∴ ∠EGD =∠EDG=∠EDB=∠EBD=45°;∴ ∠AGD=∠FDB=135°.∵ ∠ACB=90°,∠AED=90°,∠ADE=∠FDC,..∠A=∠F.在△ADG和△FBD中,
LACGLEFCCLEFDEACFBD(AAS),∴AACDF. CABCECEFBD(AAS),∴AACDF.
(2)DM=AB.证明:∵ DE=EB,EG=EB,∴DE=EB=EG.∵ DE⊥AB,∴ ∠GEM=90°.∵ GH⊥AD,.. ∠AHG=90°.又∵ ∠AGH=∠EGM,∴ ∠A=∠M.在△AED 和△MEG 中, ∴ △AED≌△MEG(AAS),∴ AE =EM,∴ AE+EB =EM+DE,即AB=DM.
14. B 解析:如图,过A作AE⊥AC,交CB 的延长线于 E, , ∠DAB =∠DCB = 90°, ∴ ∠D + ∠ABC =180°= ∠ABE + ∠ABC. ∴ ∠D = D ∠ABE. 又∵ ∠DAB=∠CAE = 90°,∴∠CAD = ∠EAB. 又∵AD = AB, C∴△ACD≌△AEB(ASA),∴AC=AE,即△ACE是等腰直角三角形,∴四边形ABCD的面积与△ACE的面积相等. 5×5=12.5,∴四边形ABCD的面积为12.5,故选 B.
15.(1)∵△ABD和△ACE都为等腰直角三角形,∴AD=AB,AE=AC,∠DAB=∠EAC = 90°,∴ ∠DAB+∠BAC = ∠EAC+∠BAC,即∠DAC=∠BAE.在△DAC和△BAE中 ∴△DAC≌△BAE(SAS).
(2)△ABC 与△ADE 的面积相等.理由如下:如图,过点 E 作 EN⊥AD,交 DA的延长线于点 N,过点 C作CM⊥AB,垂足为M,∵ △ABD 和△ACE 都是等腰直角三 角形,∴ ∠BAD = ∠CAE = 90°,AB = AD,AC = AE.∵ ∠BAD + ∠CAE +∠BAC+∠DAE=360°,.、∠BAC+∠DAE=180°∴∠DAE+∠EAN=180°,∴ ∠BAC= BL∠EAN.在△ACM和△AEN中, . △ACM≌△AEN
(3)(a+2b) 解析:由(2)知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和,..这条小路的面积为(a+2b)m .
第3课时 三角形全等的判定(3)“ASA”与“AAS”
1.如图,小周书上的三角形被墨迹污染了一部分,他根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是 ( )
A. SSS B. SAS C. AAS D. ASA
2.如图,已知AB=AC,点D,E分别在线段AB,AC上,BE与CD相交于点O,添加以下哪个条件仍不能判定△ABE≌△ACD ( )
A.∠B=∠C B.∠AEB=∠ADC
C. BD=CE D. BE=CD
3.如图,已知∠ACD=∠BCE,AC=DC,当添加条件 时,可依据“ASA”证明△ACB≌△DCE;当添加条件 时,可依据“AAS”证明△ACB≌△DCE. (不添加辅助线和字母)
4.如图,AB∥CF,E为DF的中点,若AB=9cm,CF=6cm,则BD= cm.
5.已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.
6.如图,在△ABC中,∠B=∠C,D是BA延长线上一点,E是AC的中点,连接DE并延长,交BC于点M,∠DAC的平分线交DM于点F.求证:AF=CM.
7.如图,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=AE.其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
8如图,AB⊥CD,且AB=CD. E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为 ( )
A. a+c B. b+c C. a-b+c D. a+b-c
9.如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-8,3),点B的坐标是 ( )
A.(2,6) B.(1,6) C.(3,8) D.(1,8)
10.如图,AB=10,∠A=∠B=45°,AC=BD= .点E,为线段AB上两点.现存在以下条件:①CE=DF=4;②AF=BE;③∠CEB=∠DFA;④CE=DF=5.请在以上条件中选择一个条件,使得△ACE一定和△BDF全等,则这个条件可以为 .(写出所有正确答案的序号)
11.如图,Rt△ABC中,∠C=90°,E为AB的中点,D为AC上一点,BF∥AC交DE的延长线于点F. AC=6,BF与AC之间的距离为5,则四边形 FBCD 周长的最小值是 .
12.如图,点B,F,C,E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.求证:AD与BE互相平分.
13.如图①,∠ACB=90°,点 D 在AC上,DE⊥AB 于 E,交BC的延长线于 F,DE=EB,EG=EB.
(1)求证:AG=DF;
(2)过点 G作GH⊥AD,垂足为H,与 DE 的延长线交于点M,如图②,找出图中与AB相等的线段,并证明.
14.如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD 的面积为 ( )
A.15 B.12.5 C.14.5 D.17
15.如图①,以△ABC的边AB,AC为边分别向外作等腰直角△ABD和等腰直角△ACE,连接CD,BE,DE.
(1)证明:△DAC≌△BAE;
(2)试判断△ABC 与△ADE 面积之间的关系,并说明理由;
(3)园林小路,曲径通幽,如图②所示,小路由白色的正方形大理石和黑色的三角形大理石铺成,已知中间的所有正方形的面积之和是a m ,内圈的所有三角形的面积之和是bm ,这条小路一共占地 m .(用含a,b的式子表示)
第3课时 三角形全等的判定(3)“ASA”与“AAS”1. D 2. D 3.∠A=∠D ∠B=∠E 4.3
5. 由∠ECB=70°得∠ACB=110°,又∵ ∠D=110°,∴ ∠ACB=∠D.∵AB∥DE,∴ ∠CAB=∠E.在△ABC 和△EAD 中, ∴△ABC≌△EAD(AAS).
6.∵ ∠B=∠C,. ∠DAC=∠B+∠C=2∠C.∵ AF是∠DAC的平分线, E 是 AC的中点,∴AE=CE. 在△AEF和△CEM中 .△AEF≌△CEM(ASA),.. AF=CM.
7. C 解析:根据三角形的内角和定理求出∠EAB=∠FAC,进而得出∠1=∠2,∴ ①正确;根据 AAS 证明△EAB≌△FAC,∴BE=CF,AB=AC,∴②正确;根据 ASA 证明△ACN≌△ABM,∴③正确;..根据已知不能推出CD=AE,∴④错误.
8. D 解析:∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠AFB=∠CED=90°,∴∠A+∠D=90°,∠C+∠D=90°,∴∠A=∠C.∵ AB=CD,∴△ABF≌△CDE(AAS),.. AF=CE=a,BF=DE=b.∵ EF=c,.. AD=AF+DF=a+(b-c)=a+b-c.
9. B 解析:如图,过点 A 和点 B分别作AD⊥OC 于 D,BE⊥OC 于 E,∴∠ACD+∠CAD =90°,∠ACD + ∠BCE = 90°, ∴ ∠CAD =∠BCE. ∵ ∠ADC = ∠CEB, ∠CAD =∠BCE, AC = BC, . △ADC ≌ △CEB(AAS),∴DC=BE,AD=CE.:点C(-2,0),点A(-8,3),∴OC=2,AD=CE=3,OD=8,∴ CD=OD-OC=6,OE=CE-OC=1,∴BE=DC=6,∴点B的坐标是(1,6).
10.②③④ 解析:②可用SAS判定.③可用AAS判定.∴ 点E,F在线段AB上,4<3√2<5,∴当CE=4时,点E的位置有两个;当CE=5时,点E的位置只有一个,①不可以,④可以.
11.16 解析:∵ E 为AB 的中点,∴BE=AE.∵ BF∥AC,∴∠EBF=∠EAD.在 △BFE 和 △ADE 中, ∴ △BFE≌△ADE(ASA),∴BF=AD.∴四边形FBCD的周长=BF+FD+CD+BC=AD+CD+FD+BC=AC+BC+FD=11+FD.当FD⊥AC时,FD最短,此时FD=5,∴四边形FBCD周长的最小值为5+11=16.
12. ∵FB=CE,∴BC=EF.又∵AB∥ED,AC∥FD,∴∠ABC=∠DEF,∠ACB = ∠DFE. 在 △ABC 和 △DEF 中, ∴△ABC≌△DEF(ASA),∴ AC=DF.在△AOC 和△DOF 中,(20022000.050,∴AO=DOF中,∴AO=DOF中,COFO △DOF(AAS),∴AO=DOF中,DO=
CO.∵BF=CE,∴BO=EO,∴AD与BE互相平分.
13.(1)∵ DE⊥AB,..∠DEG=∠DEB=90°.又 DE=DE,EG=EB,∴△DEG≌△DEB(SAS),.. DG=DB,∠DGB=∠DBG.取GD中点P,连接 EP, 在 △EDP 和 △EGP 中, . . △EDP≌△EGP,∴∠EGD =∠EDG.又∠DEG=90°,∴ ∠EGD =∠EDG=∠EDB=∠EBD=45°;∴ ∠AGD=∠FDB=135°.∵ ∠ACB=90°,∠AED=90°,∠ADE=∠FDC,..∠A=∠F.在△ADG和△FBD中,
LACGLEFCCLEFDEACFBD(AAS),∴AACDF. CABCECEFBD(AAS),∴AACDF.
(2)DM=AB.证明:∵ DE=EB,EG=EB,∴DE=EB=EG.∵ DE⊥AB,∴ ∠GEM=90°.∵ GH⊥AD,.. ∠AHG=90°.又∵ ∠AGH=∠EGM,∴ ∠A=∠M.在△AED 和△MEG 中, ∴ △AED≌△MEG(AAS),∴ AE =EM,∴ AE+EB =EM+DE,即AB=DM.
14. B 解析:如图,过A作AE⊥AC,交CB 的延长线于 E, , ∠DAB =∠DCB = 90°, ∴ ∠D + ∠ABC =180°= ∠ABE + ∠ABC. ∴ ∠D = D ∠ABE. 又∵ ∠DAB=∠CAE = 90°,∴∠CAD = ∠EAB. 又∵AD = AB, C∴△ACD≌△AEB(ASA),∴AC=AE,即△ACE是等腰直角三角形,∴四边形ABCD的面积与△ACE的面积相等. 5×5=12.5,∴四边形ABCD的面积为12.5,故选 B.
15.(1)∵△ABD和△ACE都为等腰直角三角形,∴AD=AB,AE=AC,∠DAB=∠EAC = 90°,∴ ∠DAB+∠BAC = ∠EAC+∠BAC,即∠DAC=∠BAE.在△DAC和△BAE中 ∴△DAC≌△BAE(SAS).
(2)△ABC 与△ADE 的面积相等.理由如下:如图,过点 E 作 EN⊥AD,交 DA的延长线于点 N,过点 C作CM⊥AB,垂足为M,∵ △ABD 和△ACE 都是等腰直角三 角形,∴ ∠BAD = ∠CAE = 90°,AB = AD,AC = AE.∵ ∠BAD + ∠CAE +∠BAC+∠DAE=360°,.、∠BAC+∠DAE=180°∴∠DAE+∠EAN=180°,∴ ∠BAC= BL∠EAN.在△ACM和△AEN中, . △ACM≌△AEN
(3)(a+2b) 解析:由(2)知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和,..这条小路的面积为(a+2b)m .
