11.2.2三角形的外角 同步练习 2024-2025学年人教版八年级数学上册(含答案)
文档属性
| 名称 | 11.2.2三角形的外角 同步练习 2024-2025学年人教版八年级数学上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 340.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 12:52:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第2课时 三角形的外角
提优点:1. 运用三角形外角的性质进行计算或证明; 2. 方程思想的应用.
1、在△ABC中,∠A、∠C与∠B的外角度数如图所示,则x的值是 ( )
A.80 B.70
C.65 D.60
2.如图,点 D 在△ABC 的边AB 的延长线上、DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是 ( )
A.24° B.59°
C.60° D.69°
3.如图,AB∥CD,∠A=54°,∠E=18°,则∠C的度数是 ( )
E
A.36° B.34°
C.32° D.30°
4.将一副三角尺按如图所示的方式摆放,则∠α的大小为 .
5.如图,在△ABC 中,AD 平分∠BAC 交 BC 于点 D,∠B=30°,∠ADC=70°,则∠C的度数是 .
6.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BOC的度数为 .
7如图,在 Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线 BE 交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点 D 作 DF∥BE,交AC的延长线于点 F,求∠F的度数.
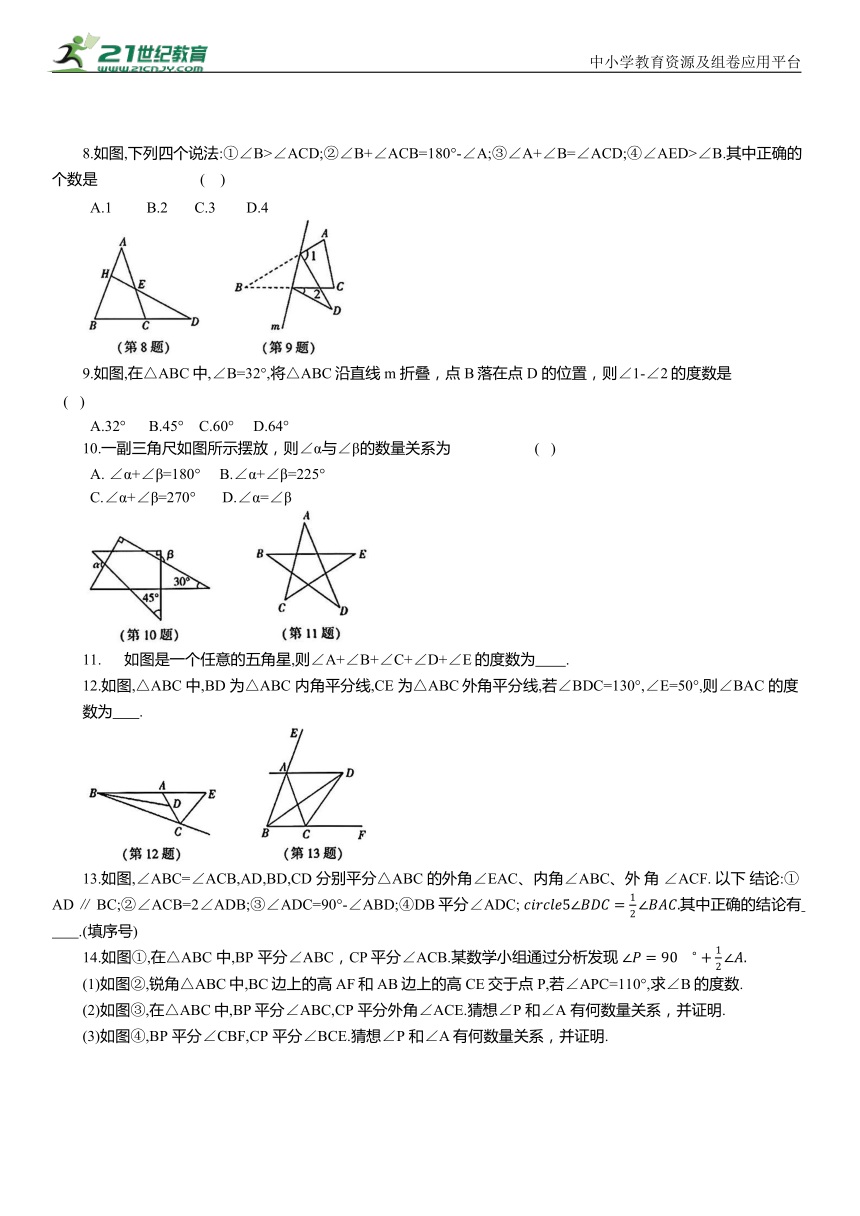
8.如图,下列四个说法:①∠B>∠ACD;②∠B+∠ACB=180°-∠A;③∠A+∠B=∠ACD;④∠AED>∠B.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
9.如图,在△ABC中,∠B=32°,将△ABC沿直线 m 折叠,点 B落在点 D 的位置,则∠1-∠2的度数是 ( )
A.32° B.45° C.60° D.64°
10.一副三角尺如图所示摆放,则∠α与∠β的数量关系为 ( )
A. ∠α+∠β=180° B.∠α+∠β=225°
C.∠α+∠β=270° D.∠α=∠β
如图是一个任意的五角星,则∠A+∠B+∠C+∠D+∠E的度数为 .
12.如图,△ABC 中,BD 为△ABC 内角平分线,CE 为△ABC外角平分线,若∠BDC=130°,∠E=50°,则∠BAC 的度数为 .
13.如图,∠ABC=∠ACB,AD,BD,CD 分别平分△ABC 的外角∠EAC、内角∠ABC、外 角 ∠ACF. 以下 结论:① AD ∥ BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④DB平分∠ADC; 其中正确的结论有 .(填序号)
14.如图①,在△ABC 中,BP 平分∠ABC,CP平分∠ACB.某数学小组通过分析发现
(1)如图②,锐角△ABC中,BC边上的高AF和AB边上的高CE交于点P,若∠APC=110°,求∠B的度数.
(2)如图③,在△ABC中,BP平分∠ABC,CP 平分外角∠ACE.猜想∠P 和∠A 有何数量关系,并证明.
(3)如图④,BP 平分∠CBF,CP 平分∠BCE.猜想∠P 和∠A有何数量关系,并证明.
第 2 课时 三角形的外角
1. B 2. B 3. A 4.75° 5.70° 6.110°
7.(1)∵ 在 Rt△ABC 中,∠ACB=90°,∠A=40°,∴ ∠CBD=90°+40°=130°.∵BE是∠CBD的平分线,∴ (2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°-65°=25°.∵DF∥BE,∴∠F=∠CEB=25°.
8. C
9. D 解析:如图,由折叠可得∠D=∠B=32°,根据外角性质得∠1=∠3+∠B,∠3=∠2+∠D,∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+64°,∴ ∠1-∠2=64°.
10. B 解析:如图,∠α=∠1+∠A=∠3+60°,∠β=∠2+∠B=∠4+30°,∵ ∠3+∠4=180°-45°=135°,∴ ∠α+∠β=135°+30°+
11.180° 解析:∵ ∠AFG 是△CEF 的外角,∴∠C+∠E=∠AFG.∴ ∠AGF是△BDG的外角,..∠B+∠D=∠AGF∴∠A+∠AFG+∠AGF=180°,∴∠A+∠B+∠C+∠D+∠E=180°.
12.120° 解析:根据三角形的外角性质,∠DBC+∠BDC=2(∠ABC+∠E),. BD 为内角平分线,∴∠DBC=∠ABD, ∠ABC130°=2(∠ABC+50°),解得 10°,∴∠BAC=∠BDC-∠ABD=130°-10°=120°.
13.①②③⑤ 解析:∵ AD 平分∠EAC,∴ ∠EAC =2∠EAD.∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,∴∠EAD=∠ABC,∴AD∥BC,∴①正确;∵AD∥BC,∴ ∠ADB=∠DBC.又∠ABC=∠ACB=2∠DBC,∴ ∠ACB=2∠ADB,∴ ②正确;∠DAC = ∠ABC+∠ACB,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC= .③正确;由②得 由③得∠BDC=∠ADC-∠ADB =90°- ∴∠ADB≠∠BDC,∴④错误;⑤正确.
14.(1) AF,CE是高,∴ ∠AFB=∠AEC=90°.∵ ∠APC=∠AEP+∠PAE,∴∠PAE=110°-90°=20°,∴∠B=90°-∠PAE=90°-20°=70°.
证明:∵ BP 是∠ABC的平分线,CP 是∠ACE 的平分线,∴ 由外角性质得∠ACE=∠1
证明:∵ P 点是外角∠CBF 和∠BCE的平分线的交点,∠P+∠PBC+∠PCB=180°,∴∠P=180°-(∠PBC+
解析:∵BA 是∠ABC 的平分线,CA 是∠ACD 的平分线, 又∠ACD=∠A+ 同理可得 则
16.(1)由题意,得CD=|0-(-3)|=3,在△BCD中,边CD的高=|0-(-2)1=2,…△BCD的面积为·
(2)∠CPQ =∠CQP.证明如下:∵ BQ 为∠CBA 的平分线,∴∠CBQ=∠ABQ.∵ AC⊥BC,..∠A=90°-∠ABC.又∠BCO=90°-∠ABC,..∠A=∠BCO.∵ ∠CPQ=∠CBQ+∠BCO,∠CQP=∠ABQ+∠A,∴∠CPQ=∠CQP.
的值不变,其值为- . 设∠ADC=∠DAC=α,∠ACE=β,∵ CE 为∠ACB 的平分线,. . ∠ACB =2∠ACE =2β,∠E=∠DAC-∠ACE=α-β,由题意显然有AB∥CD,∴∠ABC=180°-∠BCD=180°-(∠ACD+∠ACB)= 180°-[(180°-2α)+2β]=
15.如图,BA 和 CA 分别是△ABC 的内角平分线和外角平分线,BA 是∠A BD 的平分线,CA 是∠A CD的平分线,BA 是∠A BD 的平分线,CA 是 ∠A CD 的 平 分 线 …… 若 ∠A = α, 则
16.如图①,A为x轴负半轴上一点,B为x轴正半轴上一点,C(0,-2),D(-3,-2).
(1)求△BCD的面积.
(2)如图②,若AC⊥BC,作∠CBA 的平分线交CO于点 P,交CA于点 Q,判断∠CPQ与∠CQP 的大小关系,并证明你的结论.
(3)如图③,若∠ADC=∠DAC,点B在x轴正半轴上任意运动,∠ACB的平分线CE交 DA 的延长线于点E,在点 B 的运动过程中, 的值是.否变化 若不变,求出其值;若变化,请说明理由.
第2课时 三角形的外角
提优点:1. 运用三角形外角的性质进行计算或证明; 2. 方程思想的应用.
1、在△ABC中,∠A、∠C与∠B的外角度数如图所示,则x的值是 ( )
A.80 B.70
C.65 D.60
2.如图,点 D 在△ABC 的边AB 的延长线上、DE∥BC.若∠A=35°,∠C=24°,则∠D的度数是 ( )
A.24° B.59°
C.60° D.69°
3.如图,AB∥CD,∠A=54°,∠E=18°,则∠C的度数是 ( )
E
A.36° B.34°
C.32° D.30°
4.将一副三角尺按如图所示的方式摆放,则∠α的大小为 .
5.如图,在△ABC 中,AD 平分∠BAC 交 BC 于点 D,∠B=30°,∠ADC=70°,则∠C的度数是 .
6.如图,∠A=50°,∠ABO=28°,∠ACO=32°,则∠BOC的度数为 .
7如图,在 Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线 BE 交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点 D 作 DF∥BE,交AC的延长线于点 F,求∠F的度数.
8.如图,下列四个说法:①∠B>∠ACD;②∠B+∠ACB=180°-∠A;③∠A+∠B=∠ACD;④∠AED>∠B.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
9.如图,在△ABC中,∠B=32°,将△ABC沿直线 m 折叠,点 B落在点 D 的位置,则∠1-∠2的度数是 ( )
A.32° B.45° C.60° D.64°
10.一副三角尺如图所示摆放,则∠α与∠β的数量关系为 ( )
A. ∠α+∠β=180° B.∠α+∠β=225°
C.∠α+∠β=270° D.∠α=∠β
如图是一个任意的五角星,则∠A+∠B+∠C+∠D+∠E的度数为 .
12.如图,△ABC 中,BD 为△ABC 内角平分线,CE 为△ABC外角平分线,若∠BDC=130°,∠E=50°,则∠BAC 的度数为 .
13.如图,∠ABC=∠ACB,AD,BD,CD 分别平分△ABC 的外角∠EAC、内角∠ABC、外 角 ∠ACF. 以下 结论:① AD ∥ BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④DB平分∠ADC; 其中正确的结论有 .(填序号)
14.如图①,在△ABC 中,BP 平分∠ABC,CP平分∠ACB.某数学小组通过分析发现
(1)如图②,锐角△ABC中,BC边上的高AF和AB边上的高CE交于点P,若∠APC=110°,求∠B的度数.
(2)如图③,在△ABC中,BP平分∠ABC,CP 平分外角∠ACE.猜想∠P 和∠A 有何数量关系,并证明.
(3)如图④,BP 平分∠CBF,CP 平分∠BCE.猜想∠P 和∠A有何数量关系,并证明.
第 2 课时 三角形的外角
1. B 2. B 3. A 4.75° 5.70° 6.110°
7.(1)∵ 在 Rt△ABC 中,∠ACB=90°,∠A=40°,∴ ∠CBD=90°+40°=130°.∵BE是∠CBD的平分线,∴ (2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°-65°=25°.∵DF∥BE,∴∠F=∠CEB=25°.
8. C
9. D 解析:如图,由折叠可得∠D=∠B=32°,根据外角性质得∠1=∠3+∠B,∠3=∠2+∠D,∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+64°,∴ ∠1-∠2=64°.
10. B 解析:如图,∠α=∠1+∠A=∠3+60°,∠β=∠2+∠B=∠4+30°,∵ ∠3+∠4=180°-45°=135°,∴ ∠α+∠β=135°+30°+
11.180° 解析:∵ ∠AFG 是△CEF 的外角,∴∠C+∠E=∠AFG.∴ ∠AGF是△BDG的外角,..∠B+∠D=∠AGF∴∠A+∠AFG+∠AGF=180°,∴∠A+∠B+∠C+∠D+∠E=180°.
12.120° 解析:根据三角形的外角性质,∠DBC+∠BDC=2(∠ABC+∠E),. BD 为内角平分线,∴∠DBC=∠ABD, ∠ABC130°=2(∠ABC+50°),解得 10°,∴∠BAC=∠BDC-∠ABD=130°-10°=120°.
13.①②③⑤ 解析:∵ AD 平分∠EAC,∴ ∠EAC =2∠EAD.∵∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,∴∠EAD=∠ABC,∴AD∥BC,∴①正确;∵AD∥BC,∴ ∠ADB=∠DBC.又∠ABC=∠ACB=2∠DBC,∴ ∠ACB=2∠ADB,∴ ②正确;∠DAC = ∠ABC+∠ACB,∠ACF=∠ABC+∠BAC,∠ABC+∠ACB+∠BAC= .③正确;由②得 由③得∠BDC=∠ADC-∠ADB =90°- ∴∠ADB≠∠BDC,∴④错误;⑤正确.
14.(1) AF,CE是高,∴ ∠AFB=∠AEC=90°.∵ ∠APC=∠AEP+∠PAE,∴∠PAE=110°-90°=20°,∴∠B=90°-∠PAE=90°-20°=70°.
证明:∵ BP 是∠ABC的平分线,CP 是∠ACE 的平分线,∴ 由外角性质得∠ACE=∠1
证明:∵ P 点是外角∠CBF 和∠BCE的平分线的交点,∠P+∠PBC+∠PCB=180°,∴∠P=180°-(∠PBC+
解析:∵BA 是∠ABC 的平分线,CA 是∠ACD 的平分线, 又∠ACD=∠A+ 同理可得 则
16.(1)由题意,得CD=|0-(-3)|=3,在△BCD中,边CD的高=|0-(-2)1=2,…△BCD的面积为·
(2)∠CPQ =∠CQP.证明如下:∵ BQ 为∠CBA 的平分线,∴∠CBQ=∠ABQ.∵ AC⊥BC,..∠A=90°-∠ABC.又∠BCO=90°-∠ABC,..∠A=∠BCO.∵ ∠CPQ=∠CBQ+∠BCO,∠CQP=∠ABQ+∠A,∴∠CPQ=∠CQP.
的值不变,其值为- . 设∠ADC=∠DAC=α,∠ACE=β,∵ CE 为∠ACB 的平分线,. . ∠ACB =2∠ACE =2β,∠E=∠DAC-∠ACE=α-β,由题意显然有AB∥CD,∴∠ABC=180°-∠BCD=180°-(∠ACD+∠ACB)= 180°-[(180°-2α)+2β]=
15.如图,BA 和 CA 分别是△ABC 的内角平分线和外角平分线,BA 是∠A BD 的平分线,CA 是∠A CD的平分线,BA 是∠A BD 的平分线,CA 是 ∠A CD 的 平 分 线 …… 若 ∠A = α, 则
16.如图①,A为x轴负半轴上一点,B为x轴正半轴上一点,C(0,-2),D(-3,-2).
(1)求△BCD的面积.
(2)如图②,若AC⊥BC,作∠CBA 的平分线交CO于点 P,交CA于点 Q,判断∠CPQ与∠CQP 的大小关系,并证明你的结论.
(3)如图③,若∠ADC=∠DAC,点B在x轴正半轴上任意运动,∠ACB的平分线CE交 DA 的延长线于点E,在点 B 的运动过程中, 的值是.否变化 若不变,求出其值;若变化,请说明理由.
