11.1.2-11.1.3 三角形的高、中线、角平分线与三角形的稳定性 2024-2025学年人教版八年级数学上册(含答案)
文档属性
| 名称 | 11.1.2-11.1.3 三角形的高、中线、角平分线与三角形的稳定性 2024-2025学年人教版八年级数学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 444.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 12:54:14 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第2课时 三角形的高、中线、角平分线与三角形的稳定性
提优点:1. 掌握三角形三线的特征及重心的概念;
2. 会解与中线有关的三角形面积问题;
3、了解三角形的稳定性.
1.下列说法正确的是 ( )
A.过三角形的顶点和它对边中点的直线,是三角形的中线
B.三角形的角平分线其实就是角的平分线
C.三角形的高就是顶点到对边的垂线
D.三角形的三条中线的交点叫做重心,重心一定在三角形内部
2.在△ABC中,∠BAC是钝角,下列图中画AC 边上的高线正确的是 ( )
3.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在 ( )
A. A,C两点之间
B. E,G两点之间
C. B,F两点之间
D. G,H两点之间
4.下列叙述正确的有 .(填序号)
①直角三角形只有一条高线;
②三角形的角平分线可能在三角形的内部或外部;
③三角形的三条高所在的直线交于一点;
④三角形的中线将三角形分成面积相等的两个小三角形;
⑤三角形的中线将三角形分成周长相等的两个小三角形.
5.若△ABC中,边AB,AC的比为3∶5,则AB,AC边上的高的比为
6.如图,已知钝角△ABC.(不必尺规作图)
(1)画BC边上的中线AD;
(2)画△ABD的角平分线BE;
(3)画△ADC的AD边上的高CF;
(4)若AD=6,CF=4,求△ABC的面积.
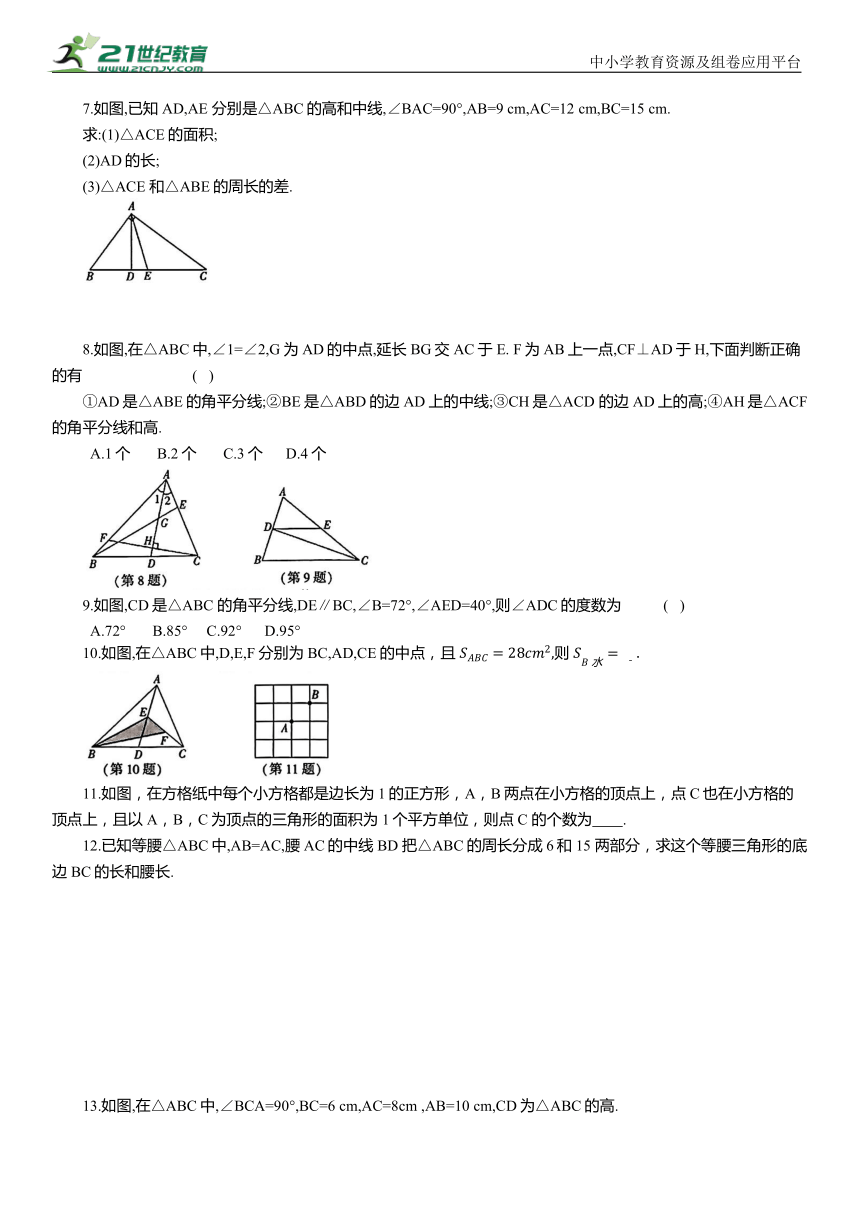
7.如图,已知 AD,AE 分别是△ABC的高和中线,∠BAC=90°,AB=9 cm,AC=12 cm,BC=15 cm.
求:(1)△ACE的面积;
(2)AD的长;
(3)△ACE 和△ABE的周长的差.
8.如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E. F为AB上一点,CF⊥AD于H,下面判断正确的有 ( )
①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD 的边AD上的高;④AH是△ACF的角平分线和高.
A.1个 B.2个 C.3个 D.4个
9.如图,CD是△ABC 的角平分线,DE∥BC,∠B=72°,∠AED=40°,则∠ADC的度数为 ( )
A.72° B.85° C.92° D.95°
10.如图,在△ABC中,D,E,F分别为BC,AD,CE的中点,且 则
11.如图,在方格纸中每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,点C也在小方格的顶点上,且以A,B,C为顶点的三角形的面积为1个平方单位,则点C 的个数为 .
12.已知等腰△ABC中,AB=AC,腰AC的中线 BD 把△ABC的周长分成6和15 两部分,求这个等腰三角形的底边 BC的长和腰长.
13.如图,在△ABC中,∠BCA=90°,BC=6 cm,AC=8cm ,AB=10 cm,CD为△ABC的高.
(1)求△ABC的面积和CD的长;
(2)若点 P从A点出发,以每秒1 cm的速度沿A→B→C 运动,点P 运动到点 C 时停止运动.设运动时间为t,问t为何值时,△PAC 的面积为6 cm
14. 如图,△ABC 的面积为 1.第一次操作:分别延长AB,BC,CA 至点A ,B ,C ,使. BC,C A=CA,顺次连接A ,B ,C ,得到 △A B C . 第二 次 操 C 作:分别延长 A B ,B C ,C A 至点 A ,B ,C ,使 顺次连接A ,B ,C ,得到△A B C ……按此规律,要使得到的三角形的面积超过2021,最少经过 次操作.
15.已知等边△ABC 和点 P,设点P 到△ABC 三边 AB,AC,BC 的距离分别为h ,h ,h ,△ABC的高为h.
(1)若点 P 在一边 BC 上,如图①,此时 求证:
(2)当点P在△ABC内,如图②,以及点 P在△ABC外,如图③,这两种情况时,上述结论是否成立 若成立,请予以证明;若不成立,h ,h ,h 与h之间又有怎样的关系 请说出你的猜想,并说明理由.
第2 课时 三角形的高、中线、角平分线与三角形的稳定性
1. D 2. D 3. B 4.③④ 5.5:3
6.(1)(2)(3)如图所示.
7.(1)∵ △ABC 是直角三角形,∠BAC= 90°,AB = 9 cm,AC = 又∵ AE 是边BC上的中线,. 即 ACE的面积是27 cm .
(2)∵ ∠BAC=90°,AD 是边 BC 上的高, 即 AD 的长为7.2 cm.
(3)∵AE 为 BC边上的中线,∴BE=CE,∴ △ACE 的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=12-9=3( cm),即△ACE和△ABE的周长的差是3 cm.
8. B 解析:①AG是△ABE的角平分线,①错误;②BG是△ABD的边AD 上的中线,②错误;③④正确.
9. C 解析:由平行线的性质得∠ADE=∠B=72°,∠AED=∠ACB=40°,∠EDC=∠DCB.又∠DCB=∠DCE=20°,∴∠ADC=∠ADE+∠EDC=92°.
10.7 cm 解析:∵点E是AD的中点,∴ 点F是CE的中点,
11.6 解析:如图,当点 C 与点 A在同一条直线上时,AC边上的高为1,AC=2,符合条件的点C有4个,即C ,C ,C ,C ;当点C与点B在同一条直线上时,BC边上的高为1,BC=2,符合条件的点C有2个,即C ,C ,所以共有6个.
12.根据题意得AB=AC,AD=CD,设BC=x,AD=CD=y,则AB=AC= 2y.①若 AB+AD = 15,BC+CD =6,则 解得 即AB=AC=10,BC=1;
②若AB+AD =6,BC+CD = 15,则 解得 即AB=AC=4,BC=13,∵4+4=8<13,不能组成三角形,舍去,∴这个等腰三角形的底边BC的长为1,腰长为10.
13.(1)△ABC的面积为- CD的长为
(2)①若CD为高,则AP= =2.5( cm),t=2.5÷1=2.5(s)②若AC为高,则CP =1.5( cm),t=(10+6-1.5)÷114.5(s).故t为2.5s或14.5s时,△PAC的面积为6cm .
14.4 解析:连接A C,如图,∵AB=A B,∴△ABC与△A BC的面积相等,∵ △ABC 面积为 1,. 2S△A BC=2,同理可得, 同理可得, 第三次操作后的面积为7×49=343,第四次操作后的面积为7×343=2401.故按此规律,要使得到的三角形的面积超过2021,最少经过4次操作.
15.(1)如图①,连接AP,则 即 又∵ △ABC是等边三角形,∴BC=AB=AC,∴h=h +h .∵ h =
(2)点 P 在△ABC 内时, 理由如下:如图②,连接AP,BP,CP,则 即 又∵ △ABC是等边三角形,∴BC=AB=
点P在△ABC外时, 理由如下:如图③,连接PB,PC,PA,由三角形的面积公式,得 即 又∵ △ABC是等边三角形,∴ 即
第2课时 三角形的高、中线、角平分线与三角形的稳定性
提优点:1. 掌握三角形三线的特征及重心的概念;
2. 会解与中线有关的三角形面积问题;
3、了解三角形的稳定性.
1.下列说法正确的是 ( )
A.过三角形的顶点和它对边中点的直线,是三角形的中线
B.三角形的角平分线其实就是角的平分线
C.三角形的高就是顶点到对边的垂线
D.三角形的三条中线的交点叫做重心,重心一定在三角形内部
2.在△ABC中,∠BAC是钝角,下列图中画AC 边上的高线正确的是 ( )
3.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在 ( )
A. A,C两点之间
B. E,G两点之间
C. B,F两点之间
D. G,H两点之间
4.下列叙述正确的有 .(填序号)
①直角三角形只有一条高线;
②三角形的角平分线可能在三角形的内部或外部;
③三角形的三条高所在的直线交于一点;
④三角形的中线将三角形分成面积相等的两个小三角形;
⑤三角形的中线将三角形分成周长相等的两个小三角形.
5.若△ABC中,边AB,AC的比为3∶5,则AB,AC边上的高的比为
6.如图,已知钝角△ABC.(不必尺规作图)
(1)画BC边上的中线AD;
(2)画△ABD的角平分线BE;
(3)画△ADC的AD边上的高CF;
(4)若AD=6,CF=4,求△ABC的面积.
7.如图,已知 AD,AE 分别是△ABC的高和中线,∠BAC=90°,AB=9 cm,AC=12 cm,BC=15 cm.
求:(1)△ACE的面积;
(2)AD的长;
(3)△ACE 和△ABE的周长的差.
8.如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E. F为AB上一点,CF⊥AD于H,下面判断正确的有 ( )
①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH是△ACD 的边AD上的高;④AH是△ACF的角平分线和高.
A.1个 B.2个 C.3个 D.4个
9.如图,CD是△ABC 的角平分线,DE∥BC,∠B=72°,∠AED=40°,则∠ADC的度数为 ( )
A.72° B.85° C.92° D.95°
10.如图,在△ABC中,D,E,F分别为BC,AD,CE的中点,且 则
11.如图,在方格纸中每个小方格都是边长为1的正方形,A,B两点在小方格的顶点上,点C也在小方格的顶点上,且以A,B,C为顶点的三角形的面积为1个平方单位,则点C 的个数为 .
12.已知等腰△ABC中,AB=AC,腰AC的中线 BD 把△ABC的周长分成6和15 两部分,求这个等腰三角形的底边 BC的长和腰长.
13.如图,在△ABC中,∠BCA=90°,BC=6 cm,AC=8cm ,AB=10 cm,CD为△ABC的高.
(1)求△ABC的面积和CD的长;
(2)若点 P从A点出发,以每秒1 cm的速度沿A→B→C 运动,点P 运动到点 C 时停止运动.设运动时间为t,问t为何值时,△PAC 的面积为6 cm
14. 如图,△ABC 的面积为 1.第一次操作:分别延长AB,BC,CA 至点A ,B ,C ,使. BC,C A=CA,顺次连接A ,B ,C ,得到 △A B C . 第二 次 操 C 作:分别延长 A B ,B C ,C A 至点 A ,B ,C ,使 顺次连接A ,B ,C ,得到△A B C ……按此规律,要使得到的三角形的面积超过2021,最少经过 次操作.
15.已知等边△ABC 和点 P,设点P 到△ABC 三边 AB,AC,BC 的距离分别为h ,h ,h ,△ABC的高为h.
(1)若点 P 在一边 BC 上,如图①,此时 求证:
(2)当点P在△ABC内,如图②,以及点 P在△ABC外,如图③,这两种情况时,上述结论是否成立 若成立,请予以证明;若不成立,h ,h ,h 与h之间又有怎样的关系 请说出你的猜想,并说明理由.
第2 课时 三角形的高、中线、角平分线与三角形的稳定性
1. D 2. D 3. B 4.③④ 5.5:3
6.(1)(2)(3)如图所示.
7.(1)∵ △ABC 是直角三角形,∠BAC= 90°,AB = 9 cm,AC = 又∵ AE 是边BC上的中线,. 即 ACE的面积是27 cm .
(2)∵ ∠BAC=90°,AD 是边 BC 上的高, 即 AD 的长为7.2 cm.
(3)∵AE 为 BC边上的中线,∴BE=CE,∴ △ACE 的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=12-9=3( cm),即△ACE和△ABE的周长的差是3 cm.
8. B 解析:①AG是△ABE的角平分线,①错误;②BG是△ABD的边AD 上的中线,②错误;③④正确.
9. C 解析:由平行线的性质得∠ADE=∠B=72°,∠AED=∠ACB=40°,∠EDC=∠DCB.又∠DCB=∠DCE=20°,∴∠ADC=∠ADE+∠EDC=92°.
10.7 cm 解析:∵点E是AD的中点,∴ 点F是CE的中点,
11.6 解析:如图,当点 C 与点 A在同一条直线上时,AC边上的高为1,AC=2,符合条件的点C有4个,即C ,C ,C ,C ;当点C与点B在同一条直线上时,BC边上的高为1,BC=2,符合条件的点C有2个,即C ,C ,所以共有6个.
12.根据题意得AB=AC,AD=CD,设BC=x,AD=CD=y,则AB=AC= 2y.①若 AB+AD = 15,BC+CD =6,则 解得 即AB=AC=10,BC=1;
②若AB+AD =6,BC+CD = 15,则 解得 即AB=AC=4,BC=13,∵4+4=8<13,不能组成三角形,舍去,∴这个等腰三角形的底边BC的长为1,腰长为10.
13.(1)△ABC的面积为- CD的长为
(2)①若CD为高,则AP= =2.5( cm),t=2.5÷1=2.5(s)②若AC为高,则CP =1.5( cm),t=(10+6-1.5)÷114.5(s).故t为2.5s或14.5s时,△PAC的面积为6cm .
14.4 解析:连接A C,如图,∵AB=A B,∴△ABC与△A BC的面积相等,∵ △ABC 面积为 1,. 2S△A BC=2,同理可得, 同理可得, 第三次操作后的面积为7×49=343,第四次操作后的面积为7×343=2401.故按此规律,要使得到的三角形的面积超过2021,最少经过4次操作.
15.(1)如图①,连接AP,则 即 又∵ △ABC是等边三角形,∴BC=AB=AC,∴h=h +h .∵ h =
(2)点 P 在△ABC 内时, 理由如下:如图②,连接AP,BP,CP,则 即 又∵ △ABC是等边三角形,∴BC=AB=
点P在△ABC外时, 理由如下:如图③,连接PB,PC,PA,由三角形的面积公式,得 即 又∵ △ABC是等边三角形,∴ 即
