第十一章三角形提优测试卷(含答案) 2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 第十一章三角形提优测试卷(含答案) 2024-2025学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 340.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十一章三角形提优测试卷
(时间:90分钟 满分:100分)
一、选择题(每小题4分,共32分)
1. 下列图形具有稳定性的是 ( )
2. 下列说法不正确的是 ( )
A.三角形的三条高线交于一点
B.直角三角形的高交于三角形的一个顶点
C.三角形的三条角平分线交于一点
D.三角形的三条中线交于一点
3.如图,△ABC中,点D为AB边上的一点,点 F为BC延长线上一点,DF交AC于点 E.下列结论中不正确的是 ( )
A.∠F+∠ACF=∠A+∠ADF
B.∠B+∠ACB<180°
C.∠DEC>∠B
D.∠A>∠ACF
4.已知△ABC的三边分别为a,b,c,且a>b>c,若b=5,c=4,则周长l的取值范围是 ( )
A.1C.145.一个多边形的边数增加1,则内角和与外角和增加的度数之和是 ( )
A.60° B.90° C.180° D.360°
6.在△ABC中,AD 是 BC边上的中线,△ADC的周长比△ABD的周长多3,AB与AC的和为13,则AC的长为 ( )
A.7 B.8 C.9 D. 10
7.如图,在△ABC中,∠ABC,∠ACB 的平分线交于点O,D 是∠ACF与∠ABC的平分线的交点,若∠BOC=120°,则∠D的度数为 ( )
A.15° B.20° C.25° D.30°
8.如图,四边形纸片ABCD中,已知∠A=160°,∠B=30°,∠C=60°,四边形纸片 ABCD 分别沿 EF,MN,OP,GH折叠,使A 与A',B 与 B',C 与 C',D 与 D'重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8的值是( )
A.600° B.700° C.720° D.800°
二、填空题(每小题4分,共24分)
9.已知a,b,c是△ABC的三边长,a,b满足 c为奇数,则c= .
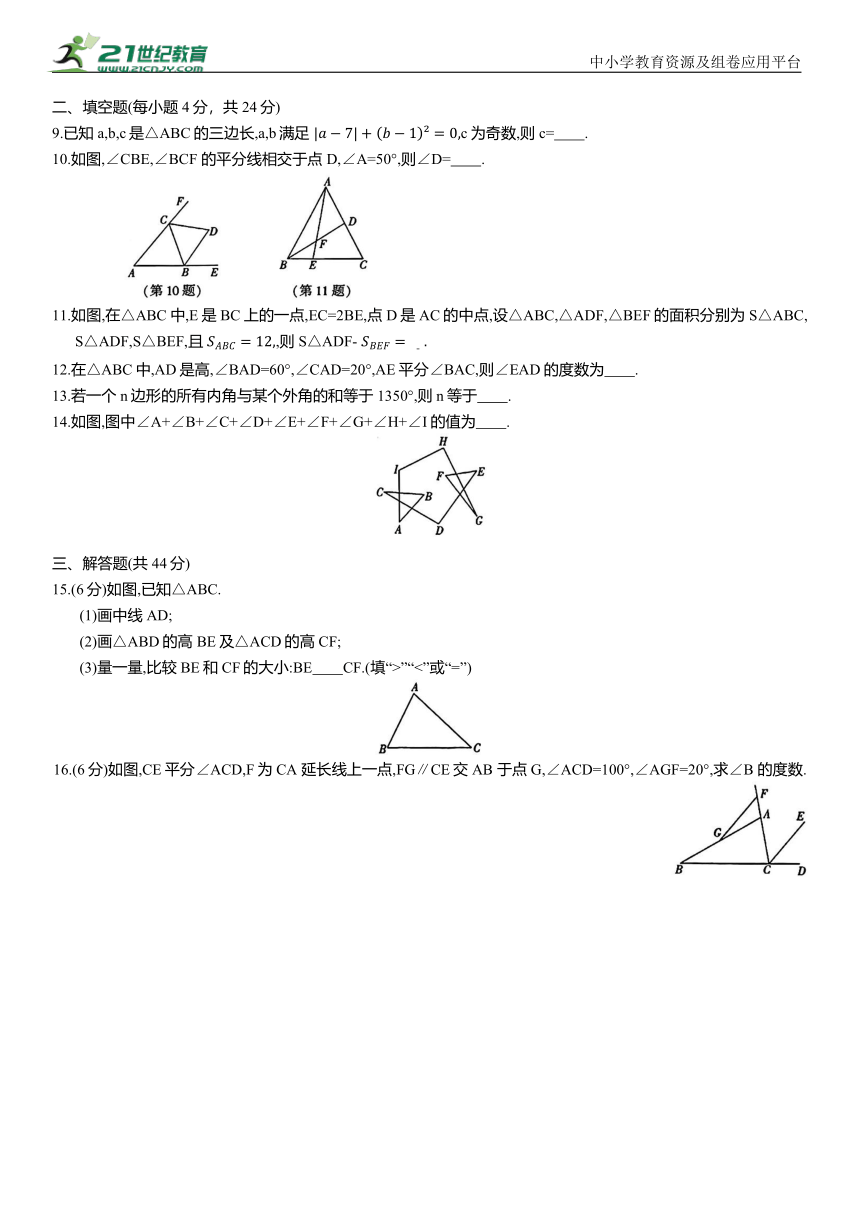
10.如图,∠CBE,∠BCF 的平分线相交于点 D,∠A=50°,则∠D= .
11.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为 S△ABC,S△ADF,S△BEF,且 ,则 S△ADF-
12.在△ABC中,AD是高,∠BAD=60°,∠CAD=20°,AE平分∠BAC,则∠EAD的度数为 .
13.若一个n边形的所有内角与某个外角的和等于1350°,则n等于 .
14.如图,图中∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的值为 .
三、解答题(共44分)
15.(6分)如图,已知△ABC.
(1)画中线AD;
(2)画△ABD的高 BE及△ACD的高CF;
(3)量一量,比较BE和CF的大小:BE CF.(填“>”“<”或“=”)
16.(6分)如图,CE平分∠ACD,F为CA 延长线上一点,FG∥CE交AB 于点G,∠ACD=100°,∠AGF=20°,求∠B 的度数.
17.(11分)小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制,第二条边长只能比第一条边长的3倍少2米.
(1)第二条边长为 米,第三条边长为 米.(用含m的式子表示)
(2)第一条边长能否为10米 为什么
(3)求m的取值范围.
18.(8分)如图所示,∠A=10°,∠ABC=90°,∠ACB=∠DCE,∠ADC=∠EDF,∠CED=∠FEG.求∠F 的度数.
19.(13分)如图,四边形ABCD中,AB∥CD,∠B=∠D,点E为BC延长线上一点,连接AE.
(1)如图①,求证:AD∥BC.
(2)①如图②,∠DAE 和∠DCE 的平分线相交于点F,连接AC.若∠BAE=70°,求∠F的度数;
②如图③,∠DCE的平分线交 AE 于点 G,连接AC,若∠BAC=∠DAE,∠AGC=2∠CAE,求∠CAE的度数.
第十一章提优测试卷
1. A 2. A 3. D 4. C 5. C 6. B 7. D
8. A 解析:∵ 四边形ABCD中,∠A=160°,∠B=30°,∠C=60°, -60°,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8=320°+220°+
9.7 10.65° 11.2
12.20°或40° 解析:如图①,当∠C 为锐角时,∠BAC=∠BAD+∠CAD=80°,∴∠BAE=40°,∴∠EAD=∠BAD-∠BAE=20°.
如图②,当∠ACB 为钝角时,∠BAC =∠BAD--∠CAD = 40°.∴∠CAE=20°,则∠EAD=∠DAC+∠EAC=40°.
13.9 解析:设这个外角度数为x,根据题意,得(n-2)×180+x=1350,解得x=1710-180n.由于014.540° 解析:设AI与BC,CD 分别交于点J,K,DE 与 GH 交于点N,则∠A+∠B=∠AJC,∠AJC+∠C=∠IKD,: ∠A+∠B+∠C=∠IKD.同理∠E+∠F+∠G=∠HND.∴∠A+∠B+∠C+∠D+∠E+∠. F+∠G+∠H+∠I=∠IKD+∠D+∠HND+∠I+∠H=540°.
15.(1)(2)如图所示.
C
(3)=
16.∵ CE平分. CE,∴∠AFG=∠ACE=50°,∴ ∠BAC=∠AFG+∠AGF =50°+20°=70°.又∠ACB=180°-∠ACD=180°-100°=80°,∴ ∠B=180°-∠BAC-∠ACB=180°-70°-80°=30°.
17.(1)(3m-2) (52-4m)
(2)不能.理由如下:若第一条边长为10米,则第二条边长为28米,第三条边长为12米,而10+12<28,不符合三角形两边之和大于第三边,∴不能构成三角形…第一条边长不能为10米.
(3)由题意,知三角形的三边长分别为m米,(3m-2)米,(52-4m)米.则 解得 由三角形两边之和大于第三边,得 解得 故 m的取值范围是
18.在△ABC中,∠A=10°,∠ABC=90°,.∠ACB=80°,∴∠DCE=∠ACB=80°.在△ACD中,∠DCE 是它的一个外角,. ∠DCE=∠A+∠ADC,∴∠ADC=70°,∴∠EDF=∠ADC=70°.在△ADE中,∠EDF是它的一个外角,. ∠EDF=∠A+∠AED,..∠AED=60°,..∠FEG=∠AED=60°。在△AEF中,∠FEG是它的一个外角,..∠FEG=∠A+∠F,..∠F=∠FEG-∠A=60°-10°=50°.
19.(1)∵AB∥CD,..∠B=∠DCE,而∠B=∠D,∴∠D=∠DCE,. AD∥BC.
(2) ① 如图 ①, 设 ∠DAF = ∠EAF = α,∠DCF=∠ECF =β,∵ AD∥BC,∴ ∠D =∠DCE=2β.∵ AB∥CD,∴ ∠BAE+∠EAD+∠D=180° ; ∠BAE=70°,∴70°+2α+2β=180°,整理得α+β=55°.∵∠DHF=∠DAH+ B∠D= ∠DCF+∠F,即 α+ 2β = ∠F+β,∴∠F=α+β=55°.
②如图②,设∠CAG=x,∠DCG=z,∠BAC=y,则 ∠EAD = y, ∠D = ∠DCE = 2z, ∠AGC =2∠CAE=2x.∵ AB∥CD ..∠AHD=∠BAH=x+y,∠ACD=∠BAC=y,x+2y+2==180°①.△ACG中,x+2x+y+z=180°,即3x+y+z=180°, B即6x+2y+2z=360° ②,②-①得5x=180°,x=36°,∴∠CAE=36°.
第十一章三角形提优测试卷
(时间:90分钟 满分:100分)
一、选择题(每小题4分,共32分)
1. 下列图形具有稳定性的是 ( )
2. 下列说法不正确的是 ( )
A.三角形的三条高线交于一点
B.直角三角形的高交于三角形的一个顶点
C.三角形的三条角平分线交于一点
D.三角形的三条中线交于一点
3.如图,△ABC中,点D为AB边上的一点,点 F为BC延长线上一点,DF交AC于点 E.下列结论中不正确的是 ( )
A.∠F+∠ACF=∠A+∠ADF
B.∠B+∠ACB<180°
C.∠DEC>∠B
D.∠A>∠ACF
4.已知△ABC的三边分别为a,b,c,且a>b>c,若b=5,c=4,则周长l的取值范围是 ( )
A.1
A.60° B.90° C.180° D.360°
6.在△ABC中,AD 是 BC边上的中线,△ADC的周长比△ABD的周长多3,AB与AC的和为13,则AC的长为 ( )
A.7 B.8 C.9 D. 10
7.如图,在△ABC中,∠ABC,∠ACB 的平分线交于点O,D 是∠ACF与∠ABC的平分线的交点,若∠BOC=120°,则∠D的度数为 ( )
A.15° B.20° C.25° D.30°
8.如图,四边形纸片ABCD中,已知∠A=160°,∠B=30°,∠C=60°,四边形纸片 ABCD 分别沿 EF,MN,OP,GH折叠,使A 与A',B 与 B',C 与 C',D 与 D'重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8的值是( )
A.600° B.700° C.720° D.800°
二、填空题(每小题4分,共24分)
9.已知a,b,c是△ABC的三边长,a,b满足 c为奇数,则c= .
10.如图,∠CBE,∠BCF 的平分线相交于点 D,∠A=50°,则∠D= .
11.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为 S△ABC,S△ADF,S△BEF,且 ,则 S△ADF-
12.在△ABC中,AD是高,∠BAD=60°,∠CAD=20°,AE平分∠BAC,则∠EAD的度数为 .
13.若一个n边形的所有内角与某个外角的和等于1350°,则n等于 .
14.如图,图中∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的值为 .
三、解答题(共44分)
15.(6分)如图,已知△ABC.
(1)画中线AD;
(2)画△ABD的高 BE及△ACD的高CF;
(3)量一量,比较BE和CF的大小:BE CF.(填“>”“<”或“=”)
16.(6分)如图,CE平分∠ACD,F为CA 延长线上一点,FG∥CE交AB 于点G,∠ACD=100°,∠AGF=20°,求∠B 的度数.
17.(11分)小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制,第二条边长只能比第一条边长的3倍少2米.
(1)第二条边长为 米,第三条边长为 米.(用含m的式子表示)
(2)第一条边长能否为10米 为什么
(3)求m的取值范围.
18.(8分)如图所示,∠A=10°,∠ABC=90°,∠ACB=∠DCE,∠ADC=∠EDF,∠CED=∠FEG.求∠F 的度数.
19.(13分)如图,四边形ABCD中,AB∥CD,∠B=∠D,点E为BC延长线上一点,连接AE.
(1)如图①,求证:AD∥BC.
(2)①如图②,∠DAE 和∠DCE 的平分线相交于点F,连接AC.若∠BAE=70°,求∠F的度数;
②如图③,∠DCE的平分线交 AE 于点 G,连接AC,若∠BAC=∠DAE,∠AGC=2∠CAE,求∠CAE的度数.
第十一章提优测试卷
1. A 2. A 3. D 4. C 5. C 6. B 7. D
8. A 解析:∵ 四边形ABCD中,∠A=160°,∠B=30°,∠C=60°, -60°,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8=320°+220°+
9.7 10.65° 11.2
12.20°或40° 解析:如图①,当∠C 为锐角时,∠BAC=∠BAD+∠CAD=80°,∴∠BAE=40°,∴∠EAD=∠BAD-∠BAE=20°.
如图②,当∠ACB 为钝角时,∠BAC =∠BAD--∠CAD = 40°.∴∠CAE=20°,则∠EAD=∠DAC+∠EAC=40°.
13.9 解析:设这个外角度数为x,根据题意,得(n-2)×180+x=1350,解得x=1710-180n.由于0
15.(1)(2)如图所示.
C
(3)=
16.∵ CE平分. CE,∴∠AFG=∠ACE=50°,∴ ∠BAC=∠AFG+∠AGF =50°+20°=70°.又∠ACB=180°-∠ACD=180°-100°=80°,∴ ∠B=180°-∠BAC-∠ACB=180°-70°-80°=30°.
17.(1)(3m-2) (52-4m)
(2)不能.理由如下:若第一条边长为10米,则第二条边长为28米,第三条边长为12米,而10+12<28,不符合三角形两边之和大于第三边,∴不能构成三角形…第一条边长不能为10米.
(3)由题意,知三角形的三边长分别为m米,(3m-2)米,(52-4m)米.则 解得 由三角形两边之和大于第三边,得 解得 故 m的取值范围是
18.在△ABC中,∠A=10°,∠ABC=90°,.∠ACB=80°,∴∠DCE=∠ACB=80°.在△ACD中,∠DCE 是它的一个外角,. ∠DCE=∠A+∠ADC,∴∠ADC=70°,∴∠EDF=∠ADC=70°.在△ADE中,∠EDF是它的一个外角,. ∠EDF=∠A+∠AED,..∠AED=60°,..∠FEG=∠AED=60°。在△AEF中,∠FEG是它的一个外角,..∠FEG=∠A+∠F,..∠F=∠FEG-∠A=60°-10°=50°.
19.(1)∵AB∥CD,..∠B=∠DCE,而∠B=∠D,∴∠D=∠DCE,. AD∥BC.
(2) ① 如图 ①, 设 ∠DAF = ∠EAF = α,∠DCF=∠ECF =β,∵ AD∥BC,∴ ∠D =∠DCE=2β.∵ AB∥CD,∴ ∠BAE+∠EAD+∠D=180° ; ∠BAE=70°,∴70°+2α+2β=180°,整理得α+β=55°.∵∠DHF=∠DAH+ B∠D= ∠DCF+∠F,即 α+ 2β = ∠F+β,∴∠F=α+β=55°.
②如图②,设∠CAG=x,∠DCG=z,∠BAC=y,则 ∠EAD = y, ∠D = ∠DCE = 2z, ∠AGC =2∠CAE=2x.∵ AB∥CD ..∠AHD=∠BAH=x+y,∠ACD=∠BAC=y,x+2y+2==180°①.△ACG中,x+2x+y+z=180°,即3x+y+z=180°, B即6x+2y+2z=360° ②,②-①得5x=180°,x=36°,∴∠CAE=36°.
