14.1全等三角形课件(共21张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 14.1全等三角形课件(共21张PPT)2024-2025学年度八年级上册沪科版数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 14:41:11 | ||
图片预览






文档简介
(共21张PPT)
沪科版
14.1 全等三角形
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.理解全等三角形的概念,能识别全等三角形中的对应边、对应角.
3.掌握全等三角形的性质并会运用.
学习目标
重点
重点
下面的两组图形分别可以完全重合吗?
可以完全重合.
新课引入
如图,按同一底版印制的两枚邮票,它们的形状相同、大小一样.
能够完全重合的两个图形,叫做全等形.
归纳
二 全等三角形的定义
新知学习
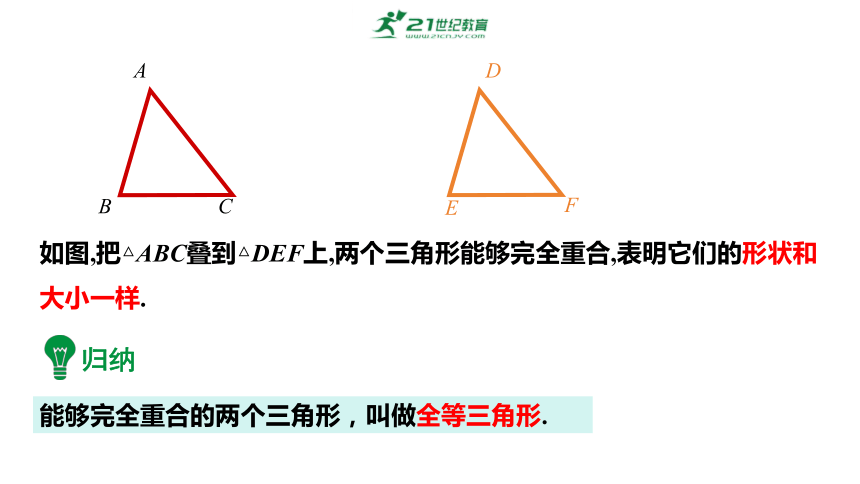
A
B
C
F
D
E
能够完全重合的两个三角形,叫做全等三角形.
如图,把△ABC叠到△DEF上,两个三角形能够完全重合,表明它们的形状和大小一样.
归纳
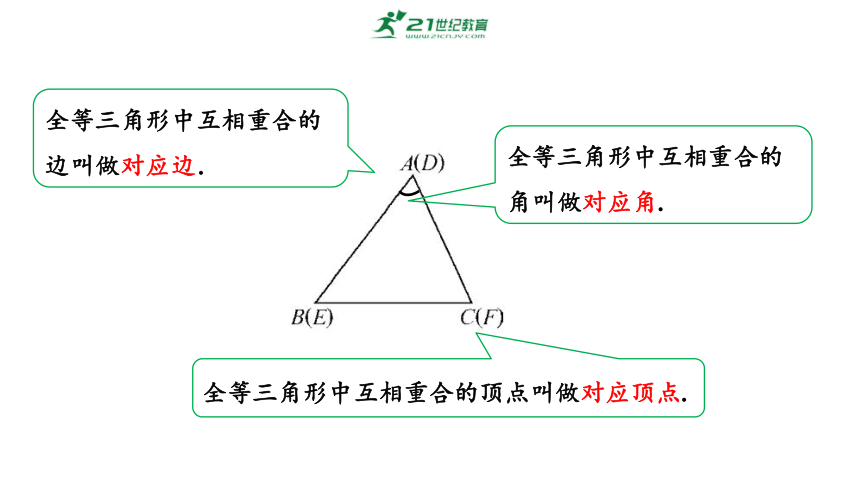
全等三角形中互相重合的边叫做对应边.
全等三角形中互相重合的角叫做对应角.
全等三角形中互相重合的顶点叫做对应顶点.
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
D
E
F
A
B
C
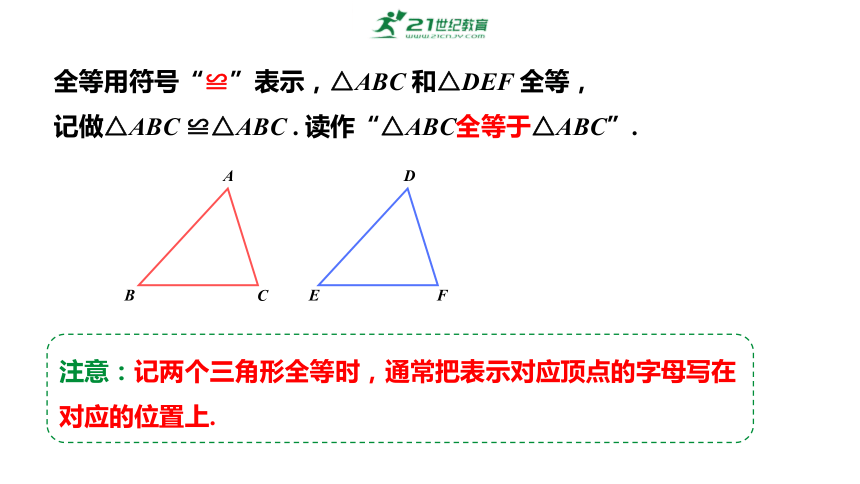
全等用符号“≌”表示,△ABC 和△DEF 全等,
记做△ABC ≌△ABC . 读作“△ABC全等于△ABC”.
二 全等三角形的性质
思考
D
E
F
A
B
C
完全重合
数学化
全等三角形的对应边相等,
全等三角形的对应角相等 .
如图,△ABC≌△DEF,对应边有什么关系?对应角呢?
归纳
全等三角形的对应边相等;全等三角形的对应角相等.
几何语言:
如图:∵△ABC≌△DEF (已知)
∴AB=DE,BC=EF,AC=DF.
∠A=∠D,∠B=∠E,∠C=∠F.
全等三角形的性质
例1 如图,△ABC≌△CDA,AB 和 CD,BC 和 DA 是对应边,写出其他对应边及对应角.
C
A
B
D
其他对应边:AC 与 CA ( 注意字母的顺序 )
对应角:∠BAC 与∠DCA,∠BCA 与∠DAC, ∠B 与∠D.
即使是同一条线段,对应端点不同,结果也是不同的含义.
例2 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1 等于多少度?
a
b
c
b
c
60°
54°
1
∠1 = 180°-54°-60°=66°.
利用全等三角形的性质求解
平移
对应边是:
AC与DF,AB与DE,BC与EF.
对应角是:
∠A与∠D,∠B与∠E,∠C与∠F.
有什么办法判断两个三角形全等?用数学式子表示两个三角形全等,并指出对应角、对应边.
思考
C
A
B
F
E
D
△ABC ≌△DEF
A
C
D
B
O
对应边是:
对应角是:
OA与OB,OC与OD,AC与BD.
∠AOC与∠BOD,∠A与∠B,∠C与∠D.
旋转
△OAC ≌△OBD
对应边是:
对应角是:
AD与AC,BD与BC,AB与AB.
∠DAB与∠CAB,∠ABD与∠ABC,∠C与∠D.
翻折
A
B
D
C
△ABC ≌△ABD
可以通过平移、旋转、翻折来判断两个三角形是否全等.
归纳
寻找全等三角形对应边、对应角的三种方法:
字母顺序法 根据书写规范,按照对应顶点确定对应边、对应角.
位置关系法 公共角(对顶角)为对应角,公共边为对应边;对应角的对边为对应边,对应边的对角为对应角.
图形特征法 最长边对最长边,最短边对最短边;最大角对最大角,最小角对最小角.
1. 如图,△ABN≌△ACM,∠B 和∠C 是对应角,AB 和 AC 是对应边.写出其他对应边及对应角.
C
B
A
M
N
对应边还有:AM 与 AN,BN 与 CM.
对应角:∠BAN 与∠CAM,∠AMC 与∠ANB.
针对训练
1.如图,△ABC≌△BAD,如果AB=5cm, BD= 4cm,AD=6cm,那么BC的长是( )
A.6cm B.5cm C.4cm D.无法确定
在上题中,∠CAB的对应角是 ( )
A.∠DAB B.∠DBA C.∠DBC D.∠CAD
A
O
C
D
B
A
B
随堂练习
2.如图,△EFG≌△NMH.
(1)请找出对应边和对应角;
(2)如果EF=2.1cm,EH=1.1cm,HN=3.3cm, 求HG的长.
解:(1)∵△EFG ≌ △NMH,
∴EF=NM,FG=MH, EG=NH
∠E=∠N, ∠F=∠M,∠FGE=∠MHN.
(2)EH=1.1cm,EG=HN=3.3cm
∴HG=EG-EH=3.3-1.1=2.2cm
N
M
F
G
E
H
分析:先根据三角形外角的性质求出
∠ ACA'=∠A+∠B=27°+40°=67°.
再由△ABC绕点C按顺时针方向旋转至△A'B'C,得到△ABC≌△A'B'C,
∴∠ACB=∠A'CB'.
∴∠ACB–∠B'CA=∠A'CB'–∠B'CA, 即∠BCB'=∠ACA'=67°.
∴∠ACB'=180°–∠ACA'–∠BCB'=180°–67°–67°=46°.
3. 如图所示,将△ABC绕点C按顺时针方向旋转至△A'B'C,使点A'落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB'为_______度.
46
全等
三角形
定义
能够完全重合的两个三角形
叫做全等三角形
基本性质
全等三角形对应边相等
全等三角形对应角相等
课堂小结
沪科版
14.1 全等三角形
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.理解全等三角形的概念,能识别全等三角形中的对应边、对应角.
3.掌握全等三角形的性质并会运用.
学习目标
重点
重点
下面的两组图形分别可以完全重合吗?
可以完全重合.
新课引入
如图,按同一底版印制的两枚邮票,它们的形状相同、大小一样.
能够完全重合的两个图形,叫做全等形.
归纳
二 全等三角形的定义
新知学习
A
B
C
F
D
E
能够完全重合的两个三角形,叫做全等三角形.
如图,把△ABC叠到△DEF上,两个三角形能够完全重合,表明它们的形状和大小一样.
归纳
全等三角形中互相重合的边叫做对应边.
全等三角形中互相重合的角叫做对应角.
全等三角形中互相重合的顶点叫做对应顶点.
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
D
E
F
A
B
C
全等用符号“≌”表示,△ABC 和△DEF 全等,
记做△ABC ≌△ABC . 读作“△ABC全等于△ABC”.
二 全等三角形的性质
思考
D
E
F
A
B
C
完全重合
数学化
全等三角形的对应边相等,
全等三角形的对应角相等 .
如图,△ABC≌△DEF,对应边有什么关系?对应角呢?
归纳
全等三角形的对应边相等;全等三角形的对应角相等.
几何语言:
如图:∵△ABC≌△DEF (已知)
∴AB=DE,BC=EF,AC=DF.
∠A=∠D,∠B=∠E,∠C=∠F.
全等三角形的性质
例1 如图,△ABC≌△CDA,AB 和 CD,BC 和 DA 是对应边,写出其他对应边及对应角.
C
A
B
D
其他对应边:AC 与 CA ( 注意字母的顺序 )
对应角:∠BAC 与∠DCA,∠BCA 与∠DAC, ∠B 与∠D.
即使是同一条线段,对应端点不同,结果也是不同的含义.
例2 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1 等于多少度?
a
b
c
b
c
60°
54°
1
∠1 = 180°-54°-60°=66°.
利用全等三角形的性质求解
平移
对应边是:
AC与DF,AB与DE,BC与EF.
对应角是:
∠A与∠D,∠B与∠E,∠C与∠F.
有什么办法判断两个三角形全等?用数学式子表示两个三角形全等,并指出对应角、对应边.
思考
C
A
B
F
E
D
△ABC ≌△DEF
A
C
D
B
O
对应边是:
对应角是:
OA与OB,OC与OD,AC与BD.
∠AOC与∠BOD,∠A与∠B,∠C与∠D.
旋转
△OAC ≌△OBD
对应边是:
对应角是:
AD与AC,BD与BC,AB与AB.
∠DAB与∠CAB,∠ABD与∠ABC,∠C与∠D.
翻折
A
B
D
C
△ABC ≌△ABD
可以通过平移、旋转、翻折来判断两个三角形是否全等.
归纳
寻找全等三角形对应边、对应角的三种方法:
字母顺序法 根据书写规范,按照对应顶点确定对应边、对应角.
位置关系法 公共角(对顶角)为对应角,公共边为对应边;对应角的对边为对应边,对应边的对角为对应角.
图形特征法 最长边对最长边,最短边对最短边;最大角对最大角,最小角对最小角.
1. 如图,△ABN≌△ACM,∠B 和∠C 是对应角,AB 和 AC 是对应边.写出其他对应边及对应角.
C
B
A
M
N
对应边还有:AM 与 AN,BN 与 CM.
对应角:∠BAN 与∠CAM,∠AMC 与∠ANB.
针对训练
1.如图,△ABC≌△BAD,如果AB=5cm, BD= 4cm,AD=6cm,那么BC的长是( )
A.6cm B.5cm C.4cm D.无法确定
在上题中,∠CAB的对应角是 ( )
A.∠DAB B.∠DBA C.∠DBC D.∠CAD
A
O
C
D
B
A
B
随堂练习
2.如图,△EFG≌△NMH.
(1)请找出对应边和对应角;
(2)如果EF=2.1cm,EH=1.1cm,HN=3.3cm, 求HG的长.
解:(1)∵△EFG ≌ △NMH,
∴EF=NM,FG=MH, EG=NH
∠E=∠N, ∠F=∠M,∠FGE=∠MHN.
(2)EH=1.1cm,EG=HN=3.3cm
∴HG=EG-EH=3.3-1.1=2.2cm
N
M
F
G
E
H
分析:先根据三角形外角的性质求出
∠ ACA'=∠A+∠B=27°+40°=67°.
再由△ABC绕点C按顺时针方向旋转至△A'B'C,得到△ABC≌△A'B'C,
∴∠ACB=∠A'CB'.
∴∠ACB–∠B'CA=∠A'CB'–∠B'CA, 即∠BCB'=∠ACA'=67°.
∴∠ACB'=180°–∠ACA'–∠BCB'=180°–67°–67°=46°.
3. 如图所示,将△ABC绕点C按顺时针方向旋转至△A'B'C,使点A'落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB'为_______度.
46
全等
三角形
定义
能够完全重合的两个三角形
叫做全等三角形
基本性质
全等三角形对应边相等
全等三角形对应角相等
课堂小结
