14.2三角形全等的判定第2课时两角及其夹边分别相等的两个三角形课件(共19张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 14.2三角形全等的判定第2课时两角及其夹边分别相等的两个三角形课件(共19张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 393.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
沪科版
14.2.2 两角及其夹边
分别相等的两个三角形
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 掌握基本事实:两角及其夹边分别相等的两个三角形全等.
2. 证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
学习目标
重点
重点
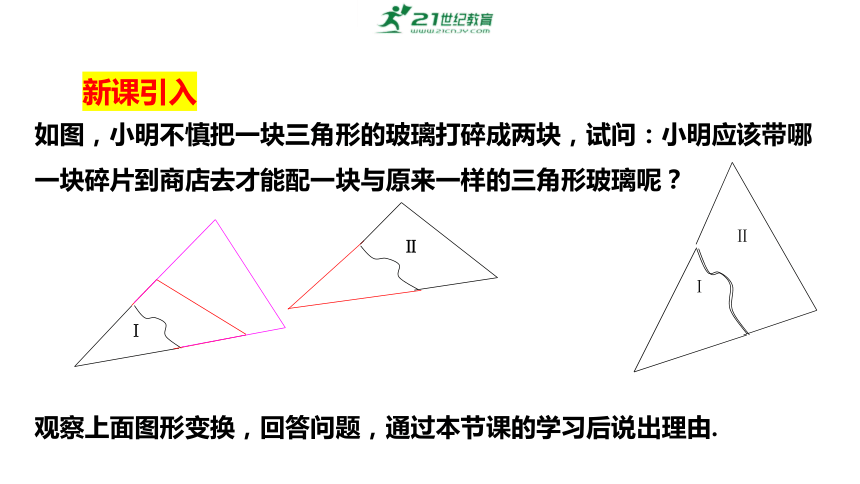
如图,小明不慎把一块三角形的玻璃打碎成两块,试问:小明应该带哪一块碎片到商店去才能配一块与原来一样的三角形玻璃呢?
Ⅰ
Ⅱ
Ⅰ
Ⅱ
观察上面图形变换,回答问题,通过本节课的学习后说出理由.
新课引入
已知:△ABC(如图).
求作:△A′B′C′,使∠B′=∠B,B′C′=BC,∠C′=∠C.
三角形全等的判定(“角边角”)
新知学习
作法:
(1)作线段B'C'=BC;
B'
C'
M
N
A'
则△A′B′C′就是所求作的三角形.
将所作的△A'B'C'与△ABC叠一叠,看看它们能否完全重合 由此你能得到什么结论
(2)在B'C'的同旁,分别以B',C'为顶点作∠MB'C' =∠ABC,
∠NC'B' = ∠C,B'M与C'N交于点A'.
现象:两个三角形能完全重合.
说明:这两个三角形全等.
两角及其夹边分别相等的两个三角形全等. 简记为“角边角”或“ASA”.
判定两个三角形全等的第2种方法是如下的基本事实.
归纳
用符号语言表达:
在△ABC 与 △A'B'C' 中
∵
∠A' = ∠A
∠B' =∠B
A'B' = AB
∴ △ABC ≌ △A'B'C' ( ASA )
A
B
C
A'
B'
C'
思考:如图,已知∠ACB=∠CBD,∠ABC=∠BDC.
能判别下面的两个三角形全等吗?
不全等,因为BC虽然是公共边,
在△ABC中,是∠ABC和∠ACB的夹边,
但在△BCD中,不是∠BDC和∠CBD的夹边.
例1 已知:如图,∠1=∠2,∠3=∠4. 求证:DB=CB.
证明:∵ ∠ ABD与∠ 3互为邻补角,
∠ABC与∠ 4互为邻补角(已知)
又∵∠3=∠4(已知)
∴ ∠ABD=∠ABC.(等角的补角相等)
在△ABD和△ABC中,
∠1= ∠2(已知)
AB=AB (公共边)
∠ DBA= ∠CBA ( 已证)
∴ △ABD ≌ △ABC (ASA)
∴ DB=CB.(全等三角形的对应边相等)
例2 已知:如图,要测量河两岸相对的两点A、B之间的距离,可以在AB的垂线BF上取两点C、D(BF在河岸上),使BC=CD,再过点D作BF的垂线DE.使点A、C、E在一条直线上,这时测得DE的长等于AB的长,请说明道理.
证明:
∵ AB⊥BD,ED ⊥ BD(已知)
∴∠ ABC=∠EDC=90°(垂直的定义)
BC=DC(已知)
在△ABC和△EDC中,
∴△ABC≌△EDC(ASA)
∴AB=ED(全等三角形的对应边相等)
∠ ABC=∠EDC (已证)
∠ ACB=∠ ECD (对顶角相等)
A
B
C
D
E
F
1.如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 __________,才能使△ABC≌△DEF (写出一个即可).
∠B=∠E
针对训练
1.如图,AB平分∠CAD,若要用“ASA”判定△ACP≌△ADP,则需增加的一个条件是__________________(写出一个即可).
∠APC=∠APD
随堂练习
2.如图,点 D 在 AB 上,点 E 在 AC 上,BA = AC,∠B =∠C.
求证:AE = AD.
目标: AE = AD
△ABE≌△ACD
A
D
B
E
C
证明:在△ABE 和△ACD 中,
∠B =∠C
AB = AC
∠A =∠A ( 公共角 )
∵△ABE ≌△ACD ( ASA )
∴AE = AD
A
D
B
E
C
3.△ABC是等腰三角形,AD、BE 分别是∠CAB、∠CBA 的平分线,△ABD和△BAE 全等吗?试说明理由.
∴ ∠BAD =∠ABE
解:∵ △ABC是等腰三角形
∴ AC=BC ∠CAB=∠CBA
又∵ AD、BE 分别是∠CAB、∠CBA 的角平分线
∴ ∠BAD= ∠CAB
∠ABE= ∠CBA
∵
∠BAD =∠ABE
∠EAB=∠DBA
AB=AB
∴△ABD≌△BAE (ASA)
用“ASA”判定
三角形全等
应用:证明角相等,边相等
基本事实:
两角及其夹边分别相等的两个三角形全等.
课堂小结
沪科版
14.2.2 两角及其夹边
分别相等的两个三角形
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 掌握基本事实:两角及其夹边分别相等的两个三角形全等.
2. 证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
学习目标
重点
重点
如图,小明不慎把一块三角形的玻璃打碎成两块,试问:小明应该带哪一块碎片到商店去才能配一块与原来一样的三角形玻璃呢?
Ⅰ
Ⅱ
Ⅰ
Ⅱ
观察上面图形变换,回答问题,通过本节课的学习后说出理由.
新课引入
已知:△ABC(如图).
求作:△A′B′C′,使∠B′=∠B,B′C′=BC,∠C′=∠C.
三角形全等的判定(“角边角”)
新知学习
作法:
(1)作线段B'C'=BC;
B'
C'
M
N
A'
则△A′B′C′就是所求作的三角形.
将所作的△A'B'C'与△ABC叠一叠,看看它们能否完全重合 由此你能得到什么结论
(2)在B'C'的同旁,分别以B',C'为顶点作∠MB'C' =∠ABC,
∠NC'B' = ∠C,B'M与C'N交于点A'.
现象:两个三角形能完全重合.
说明:这两个三角形全等.
两角及其夹边分别相等的两个三角形全等. 简记为“角边角”或“ASA”.
判定两个三角形全等的第2种方法是如下的基本事实.
归纳
用符号语言表达:
在△ABC 与 △A'B'C' 中
∵
∠A' = ∠A
∠B' =∠B
A'B' = AB
∴ △ABC ≌ △A'B'C' ( ASA )
A
B
C
A'
B'
C'
思考:如图,已知∠ACB=∠CBD,∠ABC=∠BDC.
能判别下面的两个三角形全等吗?
不全等,因为BC虽然是公共边,
在△ABC中,是∠ABC和∠ACB的夹边,
但在△BCD中,不是∠BDC和∠CBD的夹边.
例1 已知:如图,∠1=∠2,∠3=∠4. 求证:DB=CB.
证明:∵ ∠ ABD与∠ 3互为邻补角,
∠ABC与∠ 4互为邻补角(已知)
又∵∠3=∠4(已知)
∴ ∠ABD=∠ABC.(等角的补角相等)
在△ABD和△ABC中,
∠1= ∠2(已知)
AB=AB (公共边)
∠ DBA= ∠CBA ( 已证)
∴ △ABD ≌ △ABC (ASA)
∴ DB=CB.(全等三角形的对应边相等)
例2 已知:如图,要测量河两岸相对的两点A、B之间的距离,可以在AB的垂线BF上取两点C、D(BF在河岸上),使BC=CD,再过点D作BF的垂线DE.使点A、C、E在一条直线上,这时测得DE的长等于AB的长,请说明道理.
证明:
∵ AB⊥BD,ED ⊥ BD(已知)
∴∠ ABC=∠EDC=90°(垂直的定义)
BC=DC(已知)
在△ABC和△EDC中,
∴△ABC≌△EDC(ASA)
∴AB=ED(全等三角形的对应边相等)
∠ ABC=∠EDC (已证)
∠ ACB=∠ ECD (对顶角相等)
A
B
C
D
E
F
1.如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 __________,才能使△ABC≌△DEF (写出一个即可).
∠B=∠E
针对训练
1.如图,AB平分∠CAD,若要用“ASA”判定△ACP≌△ADP,则需增加的一个条件是__________________(写出一个即可).
∠APC=∠APD
随堂练习
2.如图,点 D 在 AB 上,点 E 在 AC 上,BA = AC,∠B =∠C.
求证:AE = AD.
目标: AE = AD
△ABE≌△ACD
A
D
B
E
C
证明:在△ABE 和△ACD 中,
∠B =∠C
AB = AC
∠A =∠A ( 公共角 )
∵△ABE ≌△ACD ( ASA )
∴AE = AD
A
D
B
E
C
3.△ABC是等腰三角形,AD、BE 分别是∠CAB、∠CBA 的平分线,△ABD和△BAE 全等吗?试说明理由.
∴ ∠BAD =∠ABE
解:∵ △ABC是等腰三角形
∴ AC=BC ∠CAB=∠CBA
又∵ AD、BE 分别是∠CAB、∠CBA 的角平分线
∴ ∠BAD= ∠CAB
∠ABE= ∠CBA
∵
∠BAD =∠ABE
∠EAB=∠DBA
AB=AB
∴△ABD≌△BAE (ASA)
用“ASA”判定
三角形全等
应用:证明角相等,边相等
基本事实:
两角及其夹边分别相等的两个三角形全等.
课堂小结
