14.2三角形全等的判定第6课时灵活运用全等三角形的性质和判定定理 课件(共21张PPT)
文档属性
| 名称 | 14.2三角形全等的判定第6课时灵活运用全等三角形的性质和判定定理 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 366.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
沪科版
灵活运用全等
三角形的性质和判定定理
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.掌握全等三角形的性质和判定定理.
2.灵活运用全等三角形的性质和判定定理解决相关问题.
学习目标
重点
重点
2.我们学习了几种证明两个三角形全等的方法?
边角边(SAS) 角边角(ASA)
边边边(SSS) 角角边(AAS)
斜边、直角边(HL)(仅适用于直角三角形)
1.全等三角形的性质是什么?
全等三角形的对应边相等;全等三角形的对应角相等.
新课引入
全等三角形的性质和判定定理的综合运用
例1 已知:如图,AB=CD,BC=DA,E,F是AC上的两点,且AE=CF.
求证:BF=DE.
分析:本题需要两次证明三角形全等,首先证明△ABC≌△CDA(SSS),得出∠1=∠2,再由“边角边”定理证明△DAE≌△BCF,最后证出BF=DE.
新知学习
证明:在△ABC和△CDA中
AB=CD(已知)
∵ BC=DA(已知)
CA=AC(公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2(全等三角形的对应角相等)
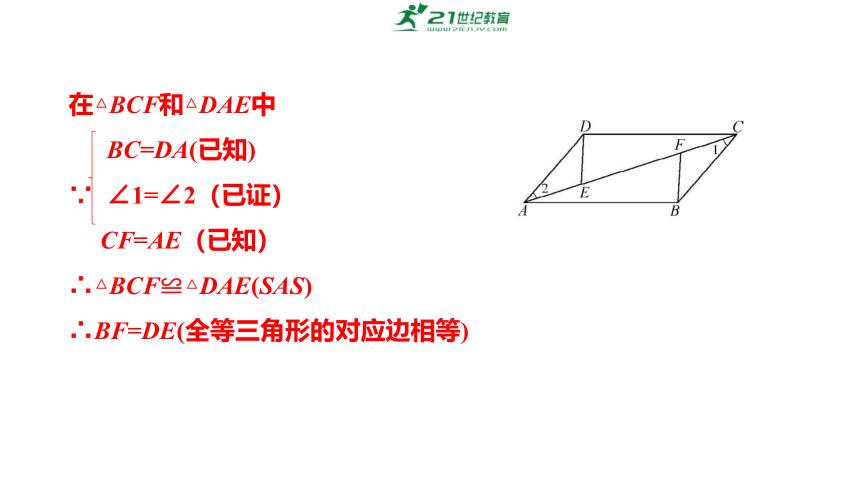
在△BCF和△DAE中
BC=DA(已知)
∵ ∠1=∠2(已证)
CF=AE(已知)
∴△BCF≌△DAE(SAS)
∴BF=DE(全等三角形的对应边相等)
例2 证明:全等三角形对应边上的高相等.
已知:如图,△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的高.
求证:AD=A′D′.
证明 ∵△ABC≌△A′B′C′(已知)
∴AB=A′B′,∠B=∠B′(全等三角形的对应边、对应角相等)
∵AD、A′D′分别是△ABC和△A′B′C′的高,
∴∠ADB=∠A′D′B′=90°(垂直的定义)
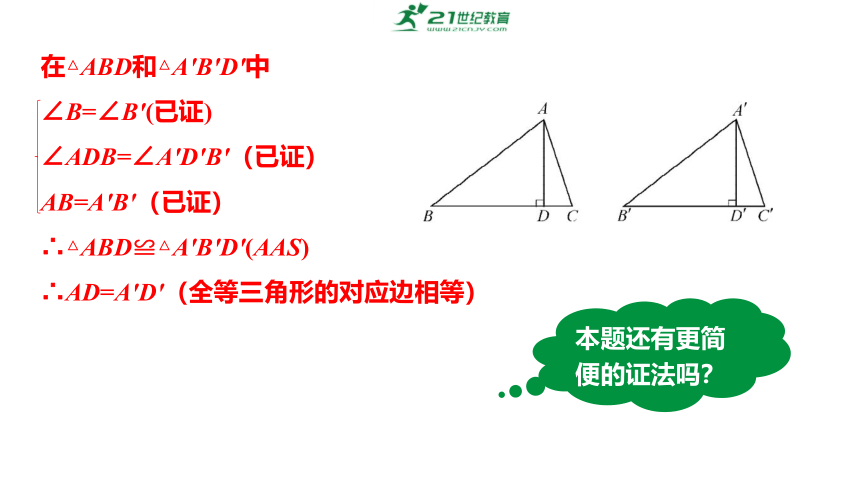
在△ABD和△A′B′D′中
∠B=∠B′(已证)
∠ADB=∠A′D′B′(已证)
AB=A′B′(已证)
∴△ABD≌△A′B′D′(AAS)
∴AD=A′D′(全等三角形的对应边相等)
本题还有更简便的证法吗?
思考
全等三角形对应边上的中线、对应角的平分线又有什么关系呢?你能说明其中的道理吗?
猜想:全等三角形对应边上的中线相等、对应角的平分线相等.
已知:如图,△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的中线.
求证:AD=A′D′.
证明
全等三角形对应边上的高相等.
证明:∵△ABC≌△A′B′C′
∴AB = AB′,∠B=∠B′,BC=B′C′
∵AD,A′D′分别是△ABC和△A′B′C′的中线.
∴BD = B′D′
△ABD≌△A′B′D′(SAS) ∴ AD = AD′
证明
全等三角形对应角的平分线相等.
已知:如图,△ABC≌△A′B′C′,BD,B′D′分别是△ABC和△A′B′C′的角平分线.求证:AD=A′D′.
证明:∵△ABC≌△A′B′C′
∴∠A=∠A′,AB = AB′,∠ABC=∠A′B′C′,
∵BD,B′D′分别是△ABC和△A′B′C′的角平分线.
∴∠ABD=∠A′B′D′,
∴△ABD≌△A′B′D′(ASA) ∴ BD = BD′
全等三角形对应边上的高线、中线、对应角的平分线分别相等.
归纳
随堂练习
1. 如图,在四边形ABCD中,AB=AD,且∠B=∠D=90°,E,F分别是BC,DC的中点,连接AE,AF,证明:AE=AF.
证明:如图,连接AC,
∵∠B=∠D=90°,
在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC(HL), ∴BC=DC
∵E,F分别是BC,DC的中点,
∴BE= BC,DF= DC,
∴BE=DF,
在△ABE和△ADF中,
∴△ABE≌△ADF(SAS),
∴AE=AF.
2. 如图,已知 CA = CB,AD = BD, M,N 分别是 CA,CB 的中点.
求证:DM = DN.
在△CAD 与△CBD 中,
CA = CB ,
AD = BD ,
CD = CD ,
证明:连接 CD,如图所示.
∴△CAD≌△CBD (SSS).
∴∠A =∠B.
又 ∵ M,N 分别是 CA,CB 的中点,
∴ AM = BN.
在△AMD 与△BND 中,
AM = BN ,
∠A =∠B ,
AD = BD ,
∴△AMD≌△BND (SAS).
∴ DM = DN.
3.如图,在△ABC中,∠A=90°,AB=AC,∠ADB=∠ECB,CE⊥BD交BD的延长线于E,求证:BD=2CE.
F
∵∠BAC=90°,CE⊥BD,
∴∠BAC=∠DEC=90°,
∵∠ADB=∠CDE,
∴∠ABD=∠DCE,
证明:如图,延长CE与BA交于点F,
在△BAD和△CAF中
F
∴△BAD≌△CAF(ASA),
∴BD=CF,∠ADB=∠F
F
∵∠ADB=∠ECB,
∴∠ECB=∠F,
在△BEF和△BEC中,
∴△BEF≌△BEC(AAS),
∴CE=EF,
∴DB=2CE.(等量代换)
对应相等的元素 两边一角 两角一边 三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边 三角形是否全等
一定
(SAS)
不一定
一定
(ASA)
一定
(AAS)
一 定
(SSS)
不一定
课堂小结
沪科版
灵活运用全等
三角形的性质和判定定理
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.掌握全等三角形的性质和判定定理.
2.灵活运用全等三角形的性质和判定定理解决相关问题.
学习目标
重点
重点
2.我们学习了几种证明两个三角形全等的方法?
边角边(SAS) 角边角(ASA)
边边边(SSS) 角角边(AAS)
斜边、直角边(HL)(仅适用于直角三角形)
1.全等三角形的性质是什么?
全等三角形的对应边相等;全等三角形的对应角相等.
新课引入
全等三角形的性质和判定定理的综合运用
例1 已知:如图,AB=CD,BC=DA,E,F是AC上的两点,且AE=CF.
求证:BF=DE.
分析:本题需要两次证明三角形全等,首先证明△ABC≌△CDA(SSS),得出∠1=∠2,再由“边角边”定理证明△DAE≌△BCF,最后证出BF=DE.
新知学习
证明:在△ABC和△CDA中
AB=CD(已知)
∵ BC=DA(已知)
CA=AC(公共边)
∴△ABC≌△CDA(SSS)
∴∠1=∠2(全等三角形的对应角相等)
在△BCF和△DAE中
BC=DA(已知)
∵ ∠1=∠2(已证)
CF=AE(已知)
∴△BCF≌△DAE(SAS)
∴BF=DE(全等三角形的对应边相等)
例2 证明:全等三角形对应边上的高相等.
已知:如图,△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的高.
求证:AD=A′D′.
证明 ∵△ABC≌△A′B′C′(已知)
∴AB=A′B′,∠B=∠B′(全等三角形的对应边、对应角相等)
∵AD、A′D′分别是△ABC和△A′B′C′的高,
∴∠ADB=∠A′D′B′=90°(垂直的定义)
在△ABD和△A′B′D′中
∠B=∠B′(已证)
∠ADB=∠A′D′B′(已证)
AB=A′B′(已证)
∴△ABD≌△A′B′D′(AAS)
∴AD=A′D′(全等三角形的对应边相等)
本题还有更简便的证法吗?
思考
全等三角形对应边上的中线、对应角的平分线又有什么关系呢?你能说明其中的道理吗?
猜想:全等三角形对应边上的中线相等、对应角的平分线相等.
已知:如图,△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的中线.
求证:AD=A′D′.
证明
全等三角形对应边上的高相等.
证明:∵△ABC≌△A′B′C′
∴AB = AB′,∠B=∠B′,BC=B′C′
∵AD,A′D′分别是△ABC和△A′B′C′的中线.
∴BD = B′D′
△ABD≌△A′B′D′(SAS) ∴ AD = AD′
证明
全等三角形对应角的平分线相等.
已知:如图,△ABC≌△A′B′C′,BD,B′D′分别是△ABC和△A′B′C′的角平分线.求证:AD=A′D′.
证明:∵△ABC≌△A′B′C′
∴∠A=∠A′,AB = AB′,∠ABC=∠A′B′C′,
∵BD,B′D′分别是△ABC和△A′B′C′的角平分线.
∴∠ABD=∠A′B′D′,
∴△ABD≌△A′B′D′(ASA) ∴ BD = BD′
全等三角形对应边上的高线、中线、对应角的平分线分别相等.
归纳
随堂练习
1. 如图,在四边形ABCD中,AB=AD,且∠B=∠D=90°,E,F分别是BC,DC的中点,连接AE,AF,证明:AE=AF.
证明:如图,连接AC,
∵∠B=∠D=90°,
在Rt△ABC和Rt△ADC中,
∴Rt△ABC≌Rt△ADC(HL), ∴BC=DC
∵E,F分别是BC,DC的中点,
∴BE= BC,DF= DC,
∴BE=DF,
在△ABE和△ADF中,
∴△ABE≌△ADF(SAS),
∴AE=AF.
2. 如图,已知 CA = CB,AD = BD, M,N 分别是 CA,CB 的中点.
求证:DM = DN.
在△CAD 与△CBD 中,
CA = CB ,
AD = BD ,
CD = CD ,
证明:连接 CD,如图所示.
∴△CAD≌△CBD (SSS).
∴∠A =∠B.
又 ∵ M,N 分别是 CA,CB 的中点,
∴ AM = BN.
在△AMD 与△BND 中,
AM = BN ,
∠A =∠B ,
AD = BD ,
∴△AMD≌△BND (SAS).
∴ DM = DN.
3.如图,在△ABC中,∠A=90°,AB=AC,∠ADB=∠ECB,CE⊥BD交BD的延长线于E,求证:BD=2CE.
F
∵∠BAC=90°,CE⊥BD,
∴∠BAC=∠DEC=90°,
∵∠ADB=∠CDE,
∴∠ABD=∠DCE,
证明:如图,延长CE与BA交于点F,
在△BAD和△CAF中
F
∴△BAD≌△CAF(ASA),
∴BD=CF,∠ADB=∠F
F
∵∠ADB=∠ECB,
∴∠ECB=∠F,
在△BEF和△BEC中,
∴△BEF≌△BEC(AAS),
∴CE=EF,
∴DB=2CE.(等量代换)
对应相等的元素 两边一角 两角一边 三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边 三角形是否全等
一定
(SAS)
不一定
一定
(ASA)
一定
(AAS)
一 定
(SSS)
不一定
课堂小结
