15.3 等腰三角形第1课时等腰三角形的性质课件(共18张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 15.3 等腰三角形第1课时等腰三角形的性质课件(共18张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 358.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
沪科版
15.3.1 等腰三角形的性质
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.了解等腰三角形的性质,掌握等腰三角形的性质定理及推论,会用定理及推论解决简单问题;
2.通过观察、操作、想象、推理和交流活动,理解等腰三角形“三线合一”等有关性质,提高几何推理意识.
学习目标
重点
难点
三角形都有什么性质?
新课引入
内角和180°
两边之和大于第三边,两边之差小于第三边
三角形是怎么分类的?
按角分:锐角三角形、直角三角形、钝角三角形
按边分:任意三角形、等腰三角形、等边三角形
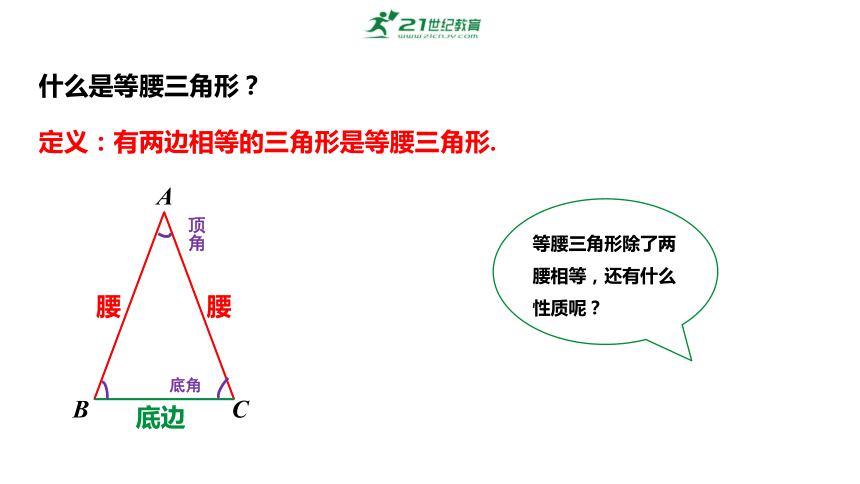
什么是等腰三角形?
定义:有两边相等的三角形是等腰三角形.
A
C
B
腰
腰
底边
等腰三角形除了两腰相等,还有什么性质呢?
顶角
底角
等腰三角形是一类特殊的三角形.等腰三角形除具有一般三角形的性质外,还具有什么样的特殊性质呢
等腰三角形是轴对称图形吗?能不能折叠?
新知学习
是轴对称图形,可以折叠
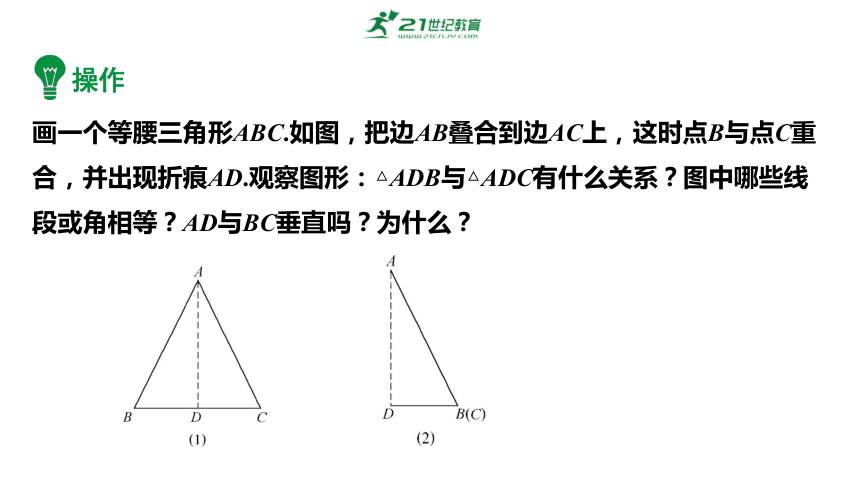
操作
画一个等腰三角形ABC.如图,把边AB叠合到边AC上,这时点B与点C重合,并出现折痕AD.观察图形:△ADB与△ADC有什么关系?图中哪些线段或角相等?AD与BC垂直吗?为什么?
∴△ADB≌△ADC(SSS)
解:在△ADB和△ADC中
AB=AC
AD=AD
BC=DC
∴∠B=∠C
∠BAD =∠CAD
∠ADB =∠ADC=90°
∴AD⊥BC
定理1 等腰三角形两个底角相等,简称“等边对等角”.
BC=DC
定理2 等腰三角形顶角的平分线垂直平分底边.
归纳
定理2 等腰三角形顶角的平分线垂直平分底边.
由此可知,等腰三角形的顶角平分线、底边上的中线和底边上的高“三线合一”.
思考:一定是顶角角平分线吗?底角角平分线有这个性质吗?
底角角平分线没有这个性质
例1 如图所示,在△ABC中,AB=AC,∠BAC=120°,点D、E是底边上两点,且BD=AD,CE=AE,求∠DAE的度数.
解:∵AB=AC,(已知)
∴∠B=∠C.(等边对等角)
∴∠B=∠C= ×(180°-120°)=30°.
又∵BD=AD,(已知)
∴∠BAD=∠B=30°.(等边对等角)
同理,∠CAE=∠C=30°
∴∠DAE=∠BAC-∠BAD-∠CAE=120°-30°-30°=60°
分析:首先应用等腰三角形的性质得到∠ABC=∠C=∠BDC,∠A=∠ABD,再运用三角形内角和定理求解得到∠A=36°,∠ABC=∠C=72°,这里可以运用代数的方法列式求解方程.
例2 已知:如图,在ΔABC中,AB=AC,点D在AC上,且BD=BC=AD,求∠A和∠C的度数.
∵AB=AC,BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.(等边对等角)
设∠A=x°,
则∠BDC=∠A+∠ABD=2x°.(三角形的一
个外角等于与它不相邻的两个内角的和)
∵∠ABC=∠C=∠BDC=2x°,
∴x+ 2x + 2x=180.(三角形内角和等于 180°)
解方程,得x= 36.
∴∠A=36°,∠C=72°.
例3 求证:斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图(1),在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,AB=A'B',AC=A'C'.
求证:Rt△ABC≌Rt△A'B'C'.
证明:在平面内移动Rt△ABC和Rt△A'B'C',使点A和点A'、点C和点C'重合,点B和点B'在AC的两侧[图(2)].
∵∠BCB'=90°+90°=180°,(等式性质)
∴B,C,B'三点在一条直线上.(平角的定义)
在△ABB'中,
∵AB=AB', (已知) ∴∠B=∠B'.(等边对等角)
在Rt△ABC和Rt△A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'. (AAS)
1.(1)等腰三角形一个底角为75°,它的另外两个角为_________;
(2)等腰三角形一个角为36°,它的另外两个角为____________________;
(3)等腰三角形一个角为120°,它的另外两个角为__________.
75°, 30°
72°,72°或36°,108°
30°,30°
随堂练习
可能为底角也可能为顶角
只可能为顶角
2.下列说法:
(1)等腰三角形的高、中线、角平分线互相重合;
(2)等腰三角形的两腰上的中线长相等;
(3)等边三角形有3条对称轴;
(4)等腰三角形的一边长为8,一边长为16,那么它的周长是32或40.
其中不正确的个数是 ( )
A.1 B.2 C.3 D.4
B
3.如图,已知△ABC为等腰三角形,BD、CE为底角的平分线,且∠DBC=∠F,求证:EC∥DF.
∴∠DBC=∠ECB.
∵∠DBC=∠F,∴∠ECB=∠F,∴EC∥DF.
证明:∵△ABC为等腰三角形,AB=AC,
∴∠ABC=∠ACB.
又∵BD、CE为底角的平分线,
定理1 等腰三角形两个底角相等,简称“等边对等角”.
定理2 等腰三角形顶角的平分线垂直平分底边(三线合一).
等腰三角形
的性质
课堂小结
沪科版
15.3.1 等腰三角形的性质
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.了解等腰三角形的性质,掌握等腰三角形的性质定理及推论,会用定理及推论解决简单问题;
2.通过观察、操作、想象、推理和交流活动,理解等腰三角形“三线合一”等有关性质,提高几何推理意识.
学习目标
重点
难点
三角形都有什么性质?
新课引入
内角和180°
两边之和大于第三边,两边之差小于第三边
三角形是怎么分类的?
按角分:锐角三角形、直角三角形、钝角三角形
按边分:任意三角形、等腰三角形、等边三角形
什么是等腰三角形?
定义:有两边相等的三角形是等腰三角形.
A
C
B
腰
腰
底边
等腰三角形除了两腰相等,还有什么性质呢?
顶角
底角
等腰三角形是一类特殊的三角形.等腰三角形除具有一般三角形的性质外,还具有什么样的特殊性质呢
等腰三角形是轴对称图形吗?能不能折叠?
新知学习
是轴对称图形,可以折叠
操作
画一个等腰三角形ABC.如图,把边AB叠合到边AC上,这时点B与点C重合,并出现折痕AD.观察图形:△ADB与△ADC有什么关系?图中哪些线段或角相等?AD与BC垂直吗?为什么?
∴△ADB≌△ADC(SSS)
解:在△ADB和△ADC中
AB=AC
AD=AD
BC=DC
∴∠B=∠C
∠BAD =∠CAD
∠ADB =∠ADC=90°
∴AD⊥BC
定理1 等腰三角形两个底角相等,简称“等边对等角”.
BC=DC
定理2 等腰三角形顶角的平分线垂直平分底边.
归纳
定理2 等腰三角形顶角的平分线垂直平分底边.
由此可知,等腰三角形的顶角平分线、底边上的中线和底边上的高“三线合一”.
思考:一定是顶角角平分线吗?底角角平分线有这个性质吗?
底角角平分线没有这个性质
例1 如图所示,在△ABC中,AB=AC,∠BAC=120°,点D、E是底边上两点,且BD=AD,CE=AE,求∠DAE的度数.
解:∵AB=AC,(已知)
∴∠B=∠C.(等边对等角)
∴∠B=∠C= ×(180°-120°)=30°.
又∵BD=AD,(已知)
∴∠BAD=∠B=30°.(等边对等角)
同理,∠CAE=∠C=30°
∴∠DAE=∠BAC-∠BAD-∠CAE=120°-30°-30°=60°
分析:首先应用等腰三角形的性质得到∠ABC=∠C=∠BDC,∠A=∠ABD,再运用三角形内角和定理求解得到∠A=36°,∠ABC=∠C=72°,这里可以运用代数的方法列式求解方程.
例2 已知:如图,在ΔABC中,AB=AC,点D在AC上,且BD=BC=AD,求∠A和∠C的度数.
∵AB=AC,BD=BC=AD,(已知)
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.(等边对等角)
设∠A=x°,
则∠BDC=∠A+∠ABD=2x°.(三角形的一
个外角等于与它不相邻的两个内角的和)
∵∠ABC=∠C=∠BDC=2x°,
∴x+ 2x + 2x=180.(三角形内角和等于 180°)
解方程,得x= 36.
∴∠A=36°,∠C=72°.
例3 求证:斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图(1),在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,AB=A'B',AC=A'C'.
求证:Rt△ABC≌Rt△A'B'C'.
证明:在平面内移动Rt△ABC和Rt△A'B'C',使点A和点A'、点C和点C'重合,点B和点B'在AC的两侧[图(2)].
∵∠BCB'=90°+90°=180°,(等式性质)
∴B,C,B'三点在一条直线上.(平角的定义)
在△ABB'中,
∵AB=AB', (已知) ∴∠B=∠B'.(等边对等角)
在Rt△ABC和Rt△A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'. (AAS)
1.(1)等腰三角形一个底角为75°,它的另外两个角为_________;
(2)等腰三角形一个角为36°,它的另外两个角为____________________;
(3)等腰三角形一个角为120°,它的另外两个角为__________.
75°, 30°
72°,72°或36°,108°
30°,30°
随堂练习
可能为底角也可能为顶角
只可能为顶角
2.下列说法:
(1)等腰三角形的高、中线、角平分线互相重合;
(2)等腰三角形的两腰上的中线长相等;
(3)等边三角形有3条对称轴;
(4)等腰三角形的一边长为8,一边长为16,那么它的周长是32或40.
其中不正确的个数是 ( )
A.1 B.2 C.3 D.4
B
3.如图,已知△ABC为等腰三角形,BD、CE为底角的平分线,且∠DBC=∠F,求证:EC∥DF.
∴∠DBC=∠ECB.
∵∠DBC=∠F,∴∠ECB=∠F,∴EC∥DF.
证明:∵△ABC为等腰三角形,AB=AC,
∴∠ABC=∠ACB.
又∵BD、CE为底角的平分线,
定理1 等腰三角形两个底角相等,简称“等边对等角”.
定理2 等腰三角形顶角的平分线垂直平分底边(三线合一).
等腰三角形
的性质
课堂小结
