13.1三角形中的边角关系第1课时三角形中边的关系课件(共22张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 13.1三角形中的边角关系第1课时三角形中边的关系课件(共22张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
沪科版
13.1.1 三角形中边的关系
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.理解三角形的定义,认识三角形的边、角、顶点;
2.能用符号语言表示三角形,能识别不同形状的三角形;
3.掌握三角形的三边关系,并能用它解决相关问题.
学习目标
重点
重点
难点
观察下面的图片,有你熟悉的几何图形吗?
新课引入
试着举出生活中其他运用三角形的例子.
一 三角形的相关概念
A
B
C
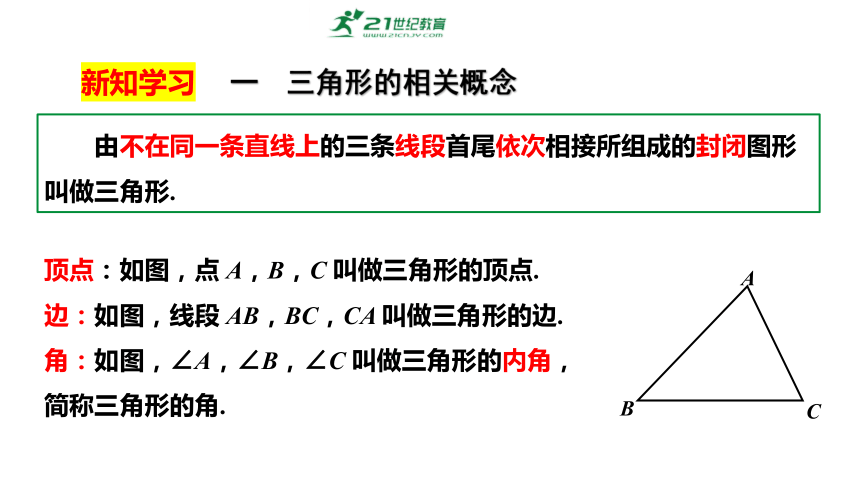
由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形.
顶点:如图,点 A,B,C 叫做三角形的顶点.
边:如图,线段 AB,BC,CA 叫做三角形的边.
角:如图,∠A,∠B,∠C 叫做三角形的内角,
简称三角形的角.
新知学习
A
B
C
a
b
c
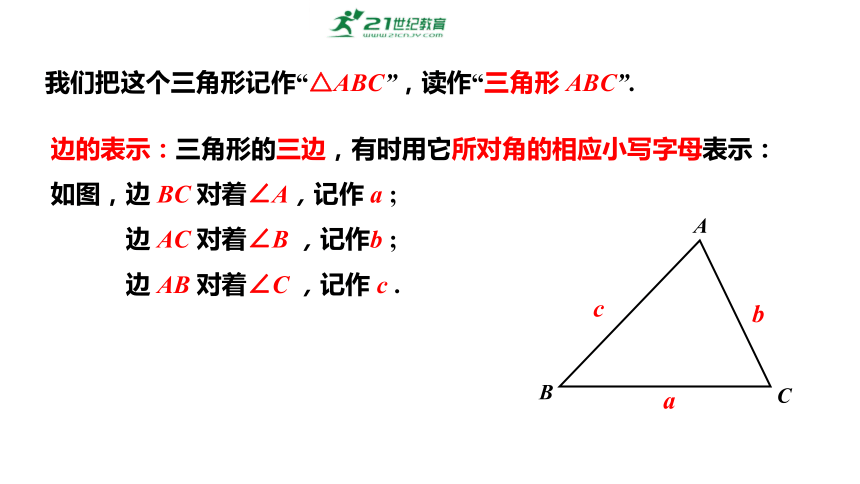
边的表示:三角形的三边,有时用它所对角的相应小写字母表示:
如图,边 BC 对着∠A,记作 a ;
边 AC 对着∠B ,记作b ;
边 AB 对着∠C ,记作 c .
我们把这个三角形记作“△ABC”,读作“三角形 ABC”.
例1 如图所示,共有 _____ 个三角形,用符号表示这些三角形为 ______________________________________________;
△ADC 的角有 ___________________;
以 AB 为边的三角形有 _______________;
以 D 为顶点的三角形有 ________________;
∠C 是 △ADC 的 _____ 边的对角;
BD 是 △ABD 中 ∠_____ 的对边.
C
D
A
B
3
△ABD
△ADC
△ABC
∠ADC
∠C
∠DAC
△ABD
△ABC
△ABD
△ADC
AD
BAD
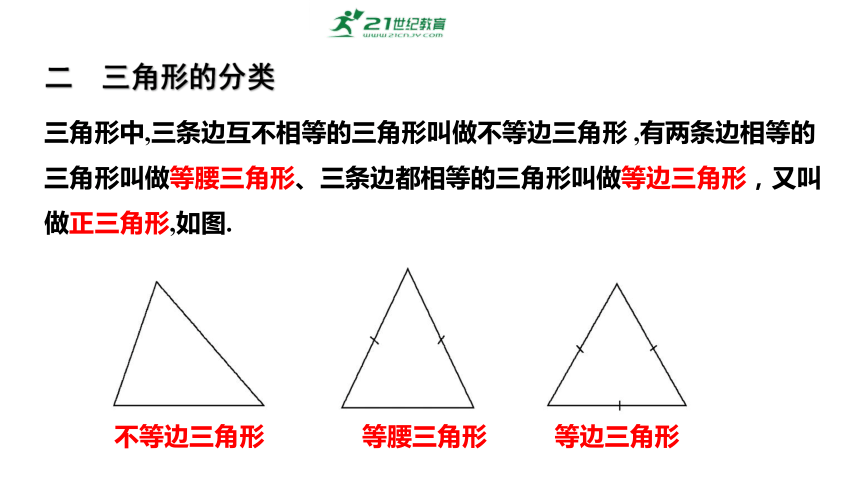
三角形中,三条边互不相等的三角形叫做不等边三角形 ,有两条边相等的三角形叫做等腰三角形、三条边都相等的三角形叫做等边三角形,又叫做正三角形,如图.
不等边三角形
等腰三角形
等边三角形
二 三角形的分类
注意:腰、底边、顶角、底角等是相对于等腰三角形来说的,
一般的三角形不存在这些概念.
腰
腰
底边
顶角
底角
底角
等腰三角形中,
腰:相等的两边叫做腰;
底边:第三边叫做底边;
顶角:两腰的夹角叫做顶角;
底角:腰和底边的夹角叫做底角.
不等边三角形
三角形
等腰三角形(等边三角形是等腰三角形的特例)
三角形按边长关系,可分为:
三角形按边长分类,还可以怎样表示?
不等边三角形
等腰
三角形
等边
三角形
例2 判断下列说法是否正确.
①等腰三角形是等边三角形; ( )
②三角形按边可分为等腰三角形、等边三角形和不等边三角形; ( )
③等腰三角形至少有两边相等; ( )
√
思考
在一个三角形中,任意两边之和与第三边的大小关系如何?你判断的根据是什么?
三 三角形的三边关系
如图,△ABC的三边长不完全一样,如果把它的任意两个顶点,例如B、C看作定点,由“两点之间,线段最短”可以得到
AB+AC>BC.
同理,得:AC+BC>AB, AB+BC>AC.
三角形中任何两边的和大于第三边.
根据不等式性质,不难得到
三角形中任何两边的差小于第三边.
归纳
总结以上,得:
注意:由三角形的三边关系可得到,三角形第三边的取值范围:
两边的差 < 第三边 < 两边的和
例3 等腰三角形中,周长为18cm.
(1)如果腰长是底边长的2倍,求各边长;
(2)如果一边长为4cm,求另两边长.
解:(1)设等腰三角形的底边长为xcm,则腰长为2xcm,根据题意,得x+2x+2x = 18
解方程,得x = 3.6
所以三角形的三边长为3.6cm,7.2cm,7.2cm.
(2)若底边长为4cm,设腰长为xcm,根据题意,得 2x+4 = 18
解方程,得:x = 7
若腰长为4cm,设底边长为xcm,,根据题意,得 2×4+x = 18
解方程,得:x = 10
由于4+4<10,可知以4cm为腰长不能构成周长为18cm的等腰三角形.
所以,三角形的另两边长都是7cm.
1.判断:用下列长度的三条线段能否组成一个三角形?
(1)1cm,2cm,3cm;
(2)2cm,3cm,4cm;
(3)4cm,5cm,6cm;
(4)5cm,6cm,10cm;
×
√
√
√
发现:判断三条线段是否可以组成三角形,只需判断两条较短线段的和是否大于第三条线段即可.
针对训练
1. 有两根长度分别为 5cm 和 8cm 的木棒,用长度为 2cm 的木棒与它们能组成三角形吗?为什么?长度为 13cm 的木棒呢?
解: ∵5 + 2 < 8,
∴长度为 2cm 的木棒与它们不能组成三角形.
∵5 + 8 = 13,
∴长度为 13cm 的木棒与它们也不能组成三角形.
随堂练习
2.已知一个三角形的两条边长分别为3cm和9cm,你能确定该三角形第三条边长的范围吗?
解:设第三条边长为a cm,则
9-3<a<9+3
即 6<a<12
所以,第三条边长的取值范围为大于6cm且小于12cm.
3.一个等腰三角形的一边是5cm,另一边是9cm,则这个三角形的周长是多少?
解:∵等腰三角形一边是5cm,另一边是9cm,
∴分两种情况讨论:
①两腰都为5cm,则周长=5+5+9=19(cm),符合题意
②两腰都为9cm,则周长=5+9+9=23(cm),也符合题意
∴这个等腰三角形的周长为19cm或23cm.
分类
定义
顶点、角、边
按边分:三边都不相等的三角形和
等腰三角形
1.判断三条线段能否组成三角形;
2.求第三边长.
三角形中
边的关系
应用
三边关系
1. 三角形两边的和大于第三边;
2. 三角形两边的差小于第三边.
课堂小结
综合实践
准备长为3cm、5cm、7cm、10cm四张纸条,试着摆出三角形,你能有多少种摆法?
沪科版
13.1.1 三角形中边的关系
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.理解三角形的定义,认识三角形的边、角、顶点;
2.能用符号语言表示三角形,能识别不同形状的三角形;
3.掌握三角形的三边关系,并能用它解决相关问题.
学习目标
重点
重点
难点
观察下面的图片,有你熟悉的几何图形吗?
新课引入
试着举出生活中其他运用三角形的例子.
一 三角形的相关概念
A
B
C
由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形.
顶点:如图,点 A,B,C 叫做三角形的顶点.
边:如图,线段 AB,BC,CA 叫做三角形的边.
角:如图,∠A,∠B,∠C 叫做三角形的内角,
简称三角形的角.
新知学习
A
B
C
a
b
c
边的表示:三角形的三边,有时用它所对角的相应小写字母表示:
如图,边 BC 对着∠A,记作 a ;
边 AC 对着∠B ,记作b ;
边 AB 对着∠C ,记作 c .
我们把这个三角形记作“△ABC”,读作“三角形 ABC”.
例1 如图所示,共有 _____ 个三角形,用符号表示这些三角形为 ______________________________________________;
△ADC 的角有 ___________________;
以 AB 为边的三角形有 _______________;
以 D 为顶点的三角形有 ________________;
∠C 是 △ADC 的 _____ 边的对角;
BD 是 △ABD 中 ∠_____ 的对边.
C
D
A
B
3
△ABD
△ADC
△ABC
∠ADC
∠C
∠DAC
△ABD
△ABC
△ABD
△ADC
AD
BAD
三角形中,三条边互不相等的三角形叫做不等边三角形 ,有两条边相等的三角形叫做等腰三角形、三条边都相等的三角形叫做等边三角形,又叫做正三角形,如图.
不等边三角形
等腰三角形
等边三角形
二 三角形的分类
注意:腰、底边、顶角、底角等是相对于等腰三角形来说的,
一般的三角形不存在这些概念.
腰
腰
底边
顶角
底角
底角
等腰三角形中,
腰:相等的两边叫做腰;
底边:第三边叫做底边;
顶角:两腰的夹角叫做顶角;
底角:腰和底边的夹角叫做底角.
不等边三角形
三角形
等腰三角形(等边三角形是等腰三角形的特例)
三角形按边长关系,可分为:
三角形按边长分类,还可以怎样表示?
不等边三角形
等腰
三角形
等边
三角形
例2 判断下列说法是否正确.
①等腰三角形是等边三角形; ( )
②三角形按边可分为等腰三角形、等边三角形和不等边三角形; ( )
③等腰三角形至少有两边相等; ( )
√
思考
在一个三角形中,任意两边之和与第三边的大小关系如何?你判断的根据是什么?
三 三角形的三边关系
如图,△ABC的三边长不完全一样,如果把它的任意两个顶点,例如B、C看作定点,由“两点之间,线段最短”可以得到
AB+AC>BC.
同理,得:AC+BC>AB, AB+BC>AC.
三角形中任何两边的和大于第三边.
根据不等式性质,不难得到
三角形中任何两边的差小于第三边.
归纳
总结以上,得:
注意:由三角形的三边关系可得到,三角形第三边的取值范围:
两边的差 < 第三边 < 两边的和
例3 等腰三角形中,周长为18cm.
(1)如果腰长是底边长的2倍,求各边长;
(2)如果一边长为4cm,求另两边长.
解:(1)设等腰三角形的底边长为xcm,则腰长为2xcm,根据题意,得x+2x+2x = 18
解方程,得x = 3.6
所以三角形的三边长为3.6cm,7.2cm,7.2cm.
(2)若底边长为4cm,设腰长为xcm,根据题意,得 2x+4 = 18
解方程,得:x = 7
若腰长为4cm,设底边长为xcm,,根据题意,得 2×4+x = 18
解方程,得:x = 10
由于4+4<10,可知以4cm为腰长不能构成周长为18cm的等腰三角形.
所以,三角形的另两边长都是7cm.
1.判断:用下列长度的三条线段能否组成一个三角形?
(1)1cm,2cm,3cm;
(2)2cm,3cm,4cm;
(3)4cm,5cm,6cm;
(4)5cm,6cm,10cm;
×
√
√
√
发现:判断三条线段是否可以组成三角形,只需判断两条较短线段的和是否大于第三条线段即可.
针对训练
1. 有两根长度分别为 5cm 和 8cm 的木棒,用长度为 2cm 的木棒与它们能组成三角形吗?为什么?长度为 13cm 的木棒呢?
解: ∵5 + 2 < 8,
∴长度为 2cm 的木棒与它们不能组成三角形.
∵5 + 8 = 13,
∴长度为 13cm 的木棒与它们也不能组成三角形.
随堂练习
2.已知一个三角形的两条边长分别为3cm和9cm,你能确定该三角形第三条边长的范围吗?
解:设第三条边长为a cm,则
9-3<a<9+3
即 6<a<12
所以,第三条边长的取值范围为大于6cm且小于12cm.
3.一个等腰三角形的一边是5cm,另一边是9cm,则这个三角形的周长是多少?
解:∵等腰三角形一边是5cm,另一边是9cm,
∴分两种情况讨论:
①两腰都为5cm,则周长=5+5+9=19(cm),符合题意
②两腰都为9cm,则周长=5+9+9=23(cm),也符合题意
∴这个等腰三角形的周长为19cm或23cm.
分类
定义
顶点、角、边
按边分:三边都不相等的三角形和
等腰三角形
1.判断三条线段能否组成三角形;
2.求第三边长.
三角形中
边的关系
应用
三边关系
1. 三角形两边的和大于第三边;
2. 三角形两边的差小于第三边.
课堂小结
综合实践
准备长为3cm、5cm、7cm、10cm四张纸条,试着摆出三角形,你能有多少种摆法?
