13.1三角形中的边角关系第2课时三角形中角的关系课件(共17张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 13.1三角形中的边角关系第2课时三角形中角的关系课件(共17张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 339.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 14:58:03 | ||
图片预览





文档简介
(共17张PPT)
沪科版
13.1.2 三角形中角的关系
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 会按照角的大小将三角形进行分类;
2. 能运用三角形内角和定理解决简单问题.
学习目标
重点
重点
我们在上节课把三角形按边进行了分类,可分为:
不等边三角形
三角形
等腰三角形(等边三角形是等腰三角形的特例)
三角形可以按角分类吗?若按角来分类,可以分为哪几类?
新课引入
三角形中,三个角都是锐角的三角形叫做锐角三角形,
有一个角是直角的三角形叫做直角三角形,
有一个角是钝角的三角形叫做钝角三角形 ,如图.
锐角三角形
直角三角形
钝角三角形
一 三角形的分类
新知学习
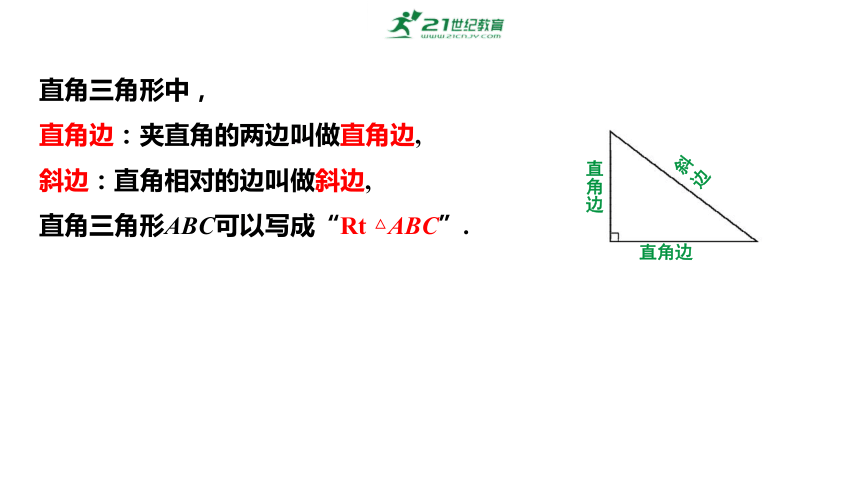
直角三角形中,
直角边:夹直角的两边叫做直角边,
斜边:直角相对的边叫做斜边,
直角三角形ABC可以写成“Rt △ABC”.
直角边
直角边
斜边
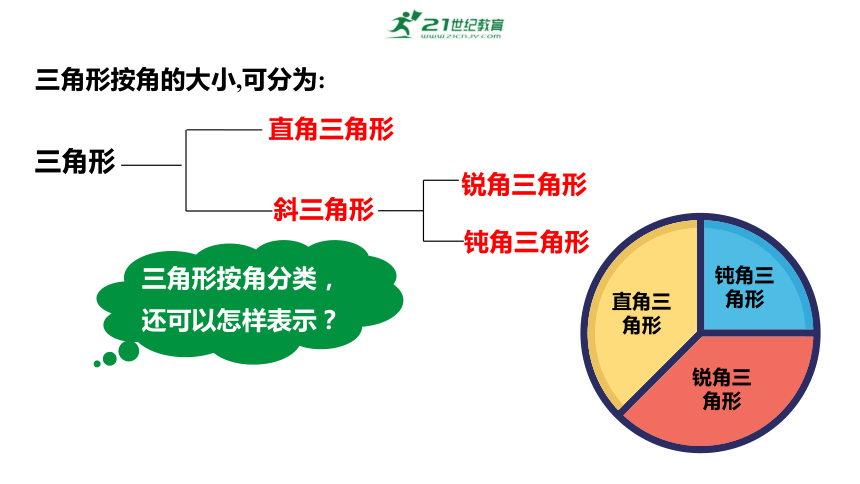
三角形按角的大小,可分为:
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
三角形按角分类,还可以怎样表示?
直角三角形
锐角三角形
钝角三角形
思考
在一个三角形中,三个内角之间有什么关系
在小学,我们曾用折叠(图1)、剪拼(图2)或用量角器度量的方法研究过这个问题.你还记得有什么结论吗
图1
图2
二 三角形的内角和
三角形的内角和等于 180°.
归纳
例1 如图,△ABC中,BD⊥AC,垂足为D,∠ABD=54°,∠DBC=18°,
求∠A和∠C的度数.
解:因为BD⊥AC,
所以∠ADB=∠CDB=90°.
在△ABD中,
∠A+∠ABD+∠ADB=180°(三角形的内角和等于 180°).
∠ABD=54°,∠ADB=90°,(已知).
∠A=180°-∠ABD-∠ADB
=180°-54°-90°=36°.
在△ABC中,
∠C=180°-∠A-(∠ABD+∠DBC)
=180°-36°-(54°+18°)=72°.
例2 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解: 设∠B为x°,则∠A为(3x)°,∠C为(x + 15)°, 从而有
3x + x +(x + 15)= 180.
解得 x = 33.
所以 3x = 99 , x + 15 = 48.
答: ∠A, ∠B, ∠C的度数分别为99°, 33°, 48°.
几何问题借助方程来解. 这是一个重要的数学思想.
1.下列各组角是同一个三角形的内角吗?为什么?
(2)60°, 40°, 90°
(3)30°, 60°, 50°
(1)3°, 150°, 27°
是
不是
不是
三角形的内角和为180°.
随堂练习
2.如图,∠1+∠2+∠3+∠4=___________ .
B
A
C
D
4
1
3
2
E
40°
(
280 °
3.如图,AB和CD交于交于点O.求证:∠A+∠C=∠B+∠D .
证明:由题意可知:
∠BOD+∠B+∠D=180°
∠AOC+∠A+∠C=180°
又因为∠BOD=∠AOC(对顶角相等)
所以∠A+∠C=∠B+∠D.
4.如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:因为DE⊥AB,所以∠FEA=90°.
因为在△AEF中,∠FEA=90°,∠A=30°,
所以∠AFE=180°-∠FEA-∠A=60°.
所以∠CFD=∠AFE=60°,
在△CDF中,
∠D=180°-∠CFD-∠FCD
=180°-60°-80°=40°.
三角形中角的关系
三角形按角分类
直角三角形
斜三角形
三角形的内角和等于180°
锐角三角形
钝角三角形
课堂小结
沪科版
13.1.2 三角形中角的关系
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 会按照角的大小将三角形进行分类;
2. 能运用三角形内角和定理解决简单问题.
学习目标
重点
重点
我们在上节课把三角形按边进行了分类,可分为:
不等边三角形
三角形
等腰三角形(等边三角形是等腰三角形的特例)
三角形可以按角分类吗?若按角来分类,可以分为哪几类?
新课引入
三角形中,三个角都是锐角的三角形叫做锐角三角形,
有一个角是直角的三角形叫做直角三角形,
有一个角是钝角的三角形叫做钝角三角形 ,如图.
锐角三角形
直角三角形
钝角三角形
一 三角形的分类
新知学习
直角三角形中,
直角边:夹直角的两边叫做直角边,
斜边:直角相对的边叫做斜边,
直角三角形ABC可以写成“Rt △ABC”.
直角边
直角边
斜边
三角形按角的大小,可分为:
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
三角形按角分类,还可以怎样表示?
直角三角形
锐角三角形
钝角三角形
思考
在一个三角形中,三个内角之间有什么关系
在小学,我们曾用折叠(图1)、剪拼(图2)或用量角器度量的方法研究过这个问题.你还记得有什么结论吗
图1
图2
二 三角形的内角和
三角形的内角和等于 180°.
归纳
例1 如图,△ABC中,BD⊥AC,垂足为D,∠ABD=54°,∠DBC=18°,
求∠A和∠C的度数.
解:因为BD⊥AC,
所以∠ADB=∠CDB=90°.
在△ABD中,
∠A+∠ABD+∠ADB=180°(三角形的内角和等于 180°).
∠ABD=54°,∠ADB=90°,(已知).
∠A=180°-∠ABD-∠ADB
=180°-54°-90°=36°.
在△ABC中,
∠C=180°-∠A-(∠ABD+∠DBC)
=180°-36°-(54°+18°)=72°.
例2 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解: 设∠B为x°,则∠A为(3x)°,∠C为(x + 15)°, 从而有
3x + x +(x + 15)= 180.
解得 x = 33.
所以 3x = 99 , x + 15 = 48.
答: ∠A, ∠B, ∠C的度数分别为99°, 33°, 48°.
几何问题借助方程来解. 这是一个重要的数学思想.
1.下列各组角是同一个三角形的内角吗?为什么?
(2)60°, 40°, 90°
(3)30°, 60°, 50°
(1)3°, 150°, 27°
是
不是
不是
三角形的内角和为180°.
随堂练习
2.如图,∠1+∠2+∠3+∠4=___________ .
B
A
C
D
4
1
3
2
E
40°
(
280 °
3.如图,AB和CD交于交于点O.求证:∠A+∠C=∠B+∠D .
证明:由题意可知:
∠BOD+∠B+∠D=180°
∠AOC+∠A+∠C=180°
又因为∠BOD=∠AOC(对顶角相等)
所以∠A+∠C=∠B+∠D.
4.如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:因为DE⊥AB,所以∠FEA=90°.
因为在△AEF中,∠FEA=90°,∠A=30°,
所以∠AFE=180°-∠FEA-∠A=60°.
所以∠CFD=∠AFE=60°,
在△CDF中,
∠D=180°-∠CFD-∠FCD
=180°-60°-80°=40°.
三角形中角的关系
三角形按角分类
直角三角形
斜三角形
三角形的内角和等于180°
锐角三角形
钝角三角形
课堂小结
