2024-2025学年吉林省长春市南关区东北师大附中明珠学校九年级(上)期初数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年吉林省长春市南关区东北师大附中明珠学校九年级(上)期初数学试卷(含答案) | 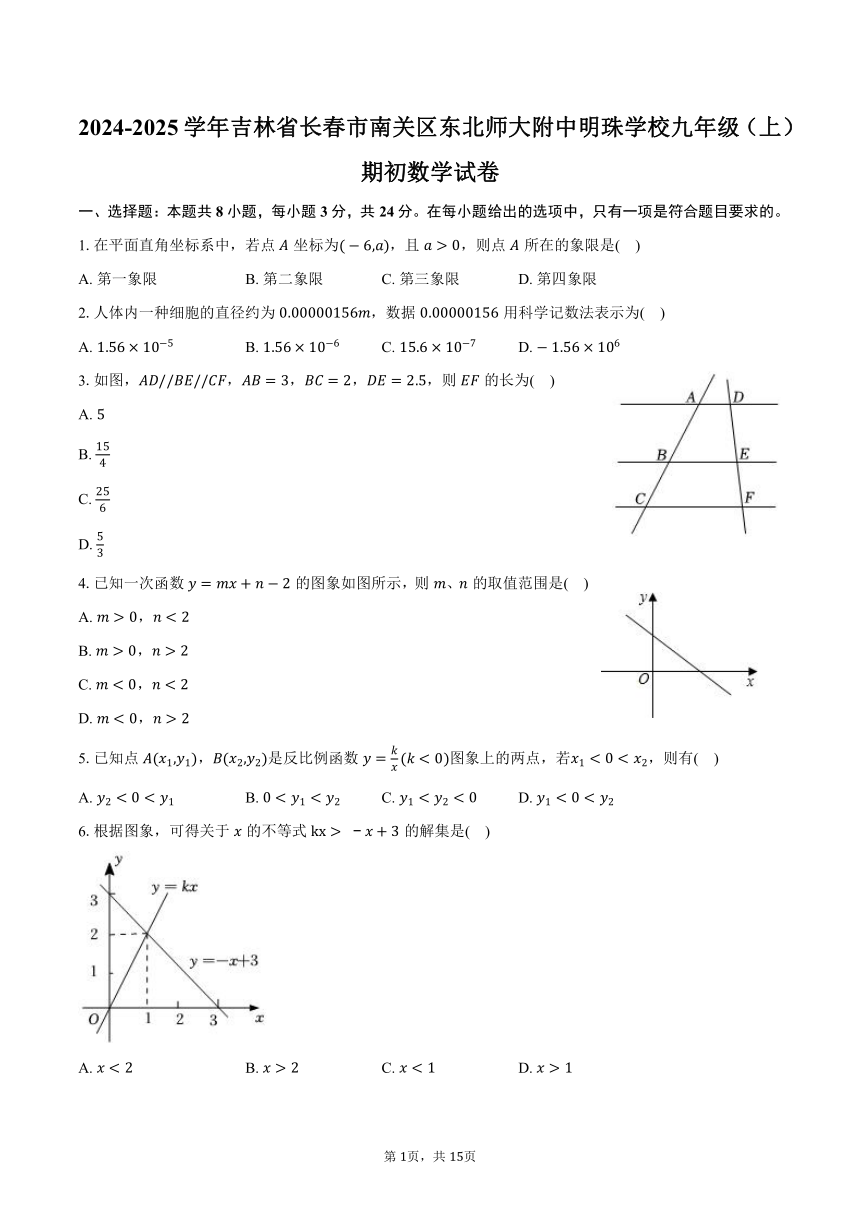 | |
| 格式 | docx | ||
| 文件大小 | 138.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 20:47:36 | ||
图片预览




文档简介
2024-2025学年吉林省长春市南关区东北师大附中明珠学校九年级(上)期初数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在平面直角坐标系中,若点坐标为,且,则点所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.人体内一种细胞的直径约为,数据用科学记数法表示为( )
A. B. C. D.
3.如图,,,,,则的长为( )
A.
B.
C.
D.
4.已知一次函数的图象如图所示,则、的取值范围是( )
A. ,
B. ,
C. ,
D. ,
5.已知点,是反比例函数图象上的两点,若,则有( )
A. B. C. D.
6.根据图象,可得关于的不等式的解集是( )
A. B. C. D.
7.如图,在 中,是上一点,交于点,的延长线交的延长线于点,,则下列结论错误的是( )
A.
B.
C.
D.
8.如图,在平面直角坐标系中,点在反比例函数的图象上,过点作轴,与反比例函数的图象交于点,点为轴上一点,连结、,若的面积为,则的值为( )
A. B.
C. D.
二、填空题:本题共6小题,每小题3分,共18分。
9.若分式有意义,则实数的取值范围是______.
10.关于的一元二次方程没有实数根是常数,则的取值范围是______.
11.若点与点关于轴对称,则______.
12.如图,线段两个端点的坐标分别为、,以原点为位似中心,将线段放大得到线段,若点的坐标为,则点的坐标为______.
13.如图,已知,和相交于点,::,则 ______.
14.如图,在平面直角坐标系中,矩形的边在轴正半轴上,点在点的左侧,直线经过点和点,且,将直线沿轴向下平移得到,若点落在矩形的内部不含边界,则的取值范围是______.
三、解答题:本题共10小题,共78分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
解方程:
;
.
16.本小题分
先化简,再求值:,其中.
17.本小题分
某商店经销一批小家电,每件成本元.经市场预测,销售定价为元时,可售出个;定价每增加元,销售量将减少个.商店若准备获利元,应涨价多少元?
18.本小题分
某中学为了解学生对“航空航天知识”的掌握情况,随机抽取名学生进行测试,对成绩百分制进行整理、描述和分析,成绩划分为,,,四个等级,并制作出不完整的统计图如下:
填空: ______, ______;
补全条形统计图;
成绩为等级人数所占扇形圆心角的大小为______
这所学校共有名学生,若全部参加这次测试,请你估计成绩在分以上含分的学生人数.
19.本小题分
图、图均是的正方形网格,每个小正方形的边长均为,每个小正方形的顶点称为格点,的顶点均在格点上只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留适当的作图痕迹.
在图中的线段上找一点,连接,使.
在图中的线段上找一点,连接,使.
在图中的线段上找一点,连接,使.
20.本小题分
如图,在锐角中,点、分别在边、上,于,于,.
求证:∽;
若,,,则 ______.
21.本小题分
,两城市之间有一条公路相连,公路途中经过市,甲车从市到市,乙车从市到市,甲车的速度比乙车的速度慢,两车距离市的路程与行驶的时间的函数图象如图所示,结合图象信息,解答下列问题:
甲车的速度是______, ______;
求图象中线段所在直线的函数解析式不需要写出自变量的取值范围;
直接写出甲车出发后几小时,两车距市的路程之和是千米.
22.本小题分
如图,一次函数的图象与反比例函数的图象交于,,与轴交于点,与轴交于点.
求反比例函数和一次函数解析式;
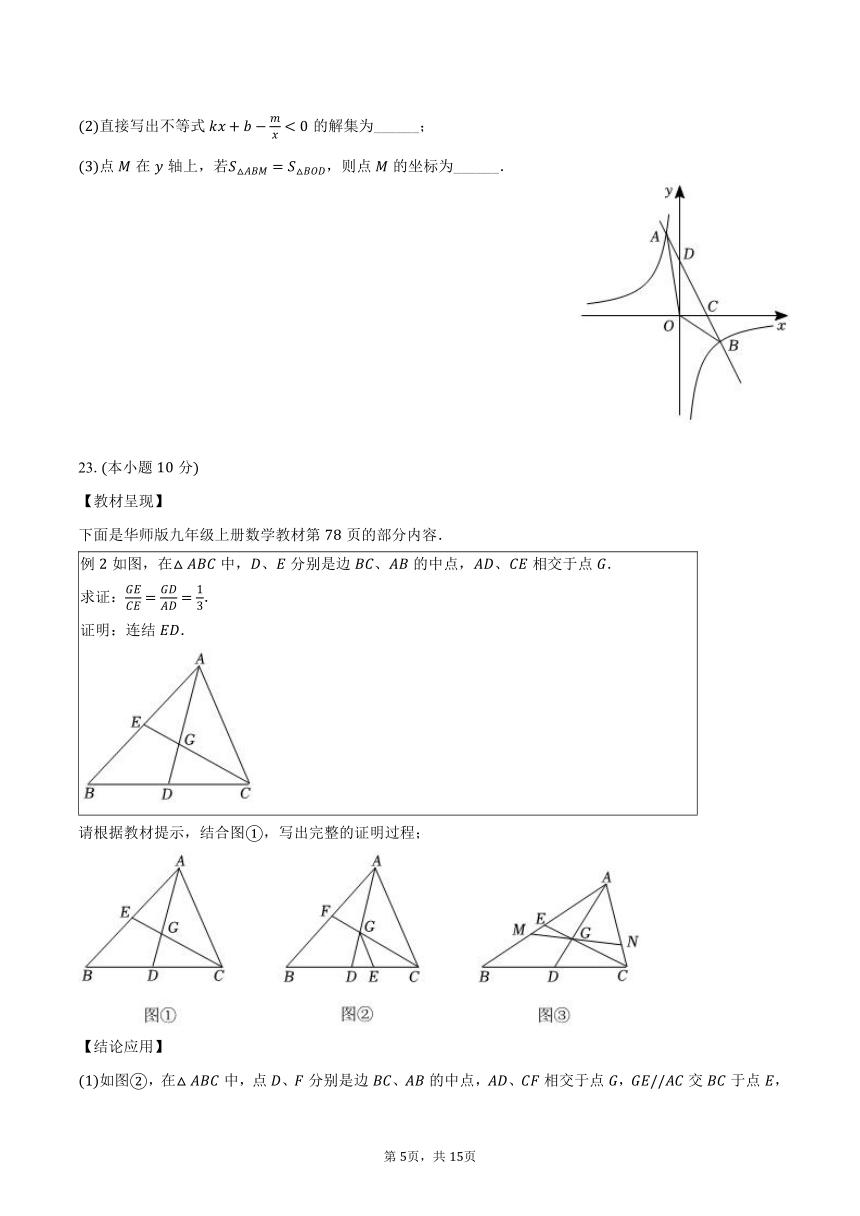
直接写出不等式的解集为______;
点在轴上,若,则点的坐标为______.
23.本小题分
【教材呈现】
下面是华师版九年级上册数学教材第页的部分内容.
例如图,在中,、分别是边、的中点,、相交于点.
求证:.
证明:连结.
请根据教材提示,结合图,写出完整的证明过程;
【结论应用】
如图,在中,点、分别是边、的中点,、相交于点,交于点,则 ______;
如图,在中,、分别是边、的中点,过点的直线分别交、于点、,若,,四边形的面积为,则 ______.
24.本小题分
如图,在中,,,点在边上运动,点关于点的对称点为点,以为边在上方作正方形设.
的长为______;
求线段的长用含的代数式表示;
当正方形与重叠部分的图形为四边形时,求的取值范围;
连结,当所在直线将正方形的面积分成:两部分时,直接写出的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.:
14.
15.解:,,,
,
,
,;
.
,
.
16.解:原式
,
当时,原式.
17.解:设每个商品的定价是元,,
由题意,得 ,
整理,得 ,
解得,符合题意.
则元,
答:应涨价元,商店可获利元.
18.,;
等级的人数:人,
补全条形统计图如图:
;
人,
答:估计成绩在分以上含分的学生人数为人.
19.解:如图,点即为所求;
如图,点即为所求;
如图,点即为所求;
20.证明:,,
,
,
,
,
∽.
解:由可知:∽,
,,
,
由可知:,
,
∽,
,
,
.
21.;;
设线段所在直线的解析式为 .
把点,代入,
得:,
解得:.
线段所在直线的函数解析式为;
,
小时,
或,
解得,
答:甲车出发小时或小时时,两车距市的路程之和是千米.
22.将代入反比例函数,
得,解得,
反比例函数的解析式为,
把代入反比例函数,可得:,
解得,
,
将,代入一次函数,
可得,解得,
一次函数的解析式为;
或;
,,
,
,
点在轴上,
设点,
则,
,
,
,
或,
点的坐标为或,
23.【教材呈现】证明:连接,如图,
、分别为、的中点,
为的中位线,
,,
∽,
,
,
即;
【结论应用】、分别是边、的中点,
,,
,
∽,
,
,
同理可得,,
.
如图,作交的延长线于点,交于点,
,,
,
,
,
∽,
,
,
,,
,
,
,
∽,
,
,
∽,
,
,
,
,
,
,
,
,,
,
,
24.;
点关于点的对称点为点,且,
分两种情况:
当时,;
当时,;
当点落在上时,如图,
,
四边形是正方形,且,
,
,
即,
解得:,
当时,正方形与重叠部分的图形为四边形;
当点落在上时,如图,
,
即,
解得:,
当时,正方形与重叠部分的图形为四边形;
综上所述,当和当时,正方形与重叠部分的图形为四边形;
的值是或.
理由:
分两种情况:
当点在边上时,,如图,
,
∽,
,即,
,
,
所在直线将正方形的面积分成:两部分,
或,
或,
解得:,大于,舍去;
.
当在的延长线上时,此时,如图,
由图可知:,,
所在直线将正方形的面积分成:两部分,
::或:,
或,
解得:,小于,舍去,
.
综上所述,的值是或.
第1页,共1页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在平面直角坐标系中,若点坐标为,且,则点所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.人体内一种细胞的直径约为,数据用科学记数法表示为( )
A. B. C. D.
3.如图,,,,,则的长为( )
A.
B.
C.
D.
4.已知一次函数的图象如图所示,则、的取值范围是( )
A. ,
B. ,
C. ,
D. ,
5.已知点,是反比例函数图象上的两点,若,则有( )
A. B. C. D.
6.根据图象,可得关于的不等式的解集是( )
A. B. C. D.
7.如图,在 中,是上一点,交于点,的延长线交的延长线于点,,则下列结论错误的是( )
A.
B.
C.
D.
8.如图,在平面直角坐标系中,点在反比例函数的图象上,过点作轴,与反比例函数的图象交于点,点为轴上一点,连结、,若的面积为,则的值为( )
A. B.
C. D.
二、填空题:本题共6小题,每小题3分,共18分。
9.若分式有意义,则实数的取值范围是______.
10.关于的一元二次方程没有实数根是常数,则的取值范围是______.
11.若点与点关于轴对称,则______.
12.如图,线段两个端点的坐标分别为、,以原点为位似中心,将线段放大得到线段,若点的坐标为,则点的坐标为______.
13.如图,已知,和相交于点,::,则 ______.
14.如图,在平面直角坐标系中,矩形的边在轴正半轴上,点在点的左侧,直线经过点和点,且,将直线沿轴向下平移得到,若点落在矩形的内部不含边界,则的取值范围是______.
三、解答题:本题共10小题,共78分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
解方程:
;
.
16.本小题分
先化简,再求值:,其中.
17.本小题分
某商店经销一批小家电,每件成本元.经市场预测,销售定价为元时,可售出个;定价每增加元,销售量将减少个.商店若准备获利元,应涨价多少元?
18.本小题分
某中学为了解学生对“航空航天知识”的掌握情况,随机抽取名学生进行测试,对成绩百分制进行整理、描述和分析,成绩划分为,,,四个等级,并制作出不完整的统计图如下:
填空: ______, ______;
补全条形统计图;
成绩为等级人数所占扇形圆心角的大小为______
这所学校共有名学生,若全部参加这次测试,请你估计成绩在分以上含分的学生人数.
19.本小题分
图、图均是的正方形网格,每个小正方形的边长均为,每个小正方形的顶点称为格点,的顶点均在格点上只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留适当的作图痕迹.
在图中的线段上找一点,连接,使.
在图中的线段上找一点,连接,使.
在图中的线段上找一点,连接,使.
20.本小题分
如图,在锐角中,点、分别在边、上,于,于,.
求证:∽;
若,,,则 ______.
21.本小题分
,两城市之间有一条公路相连,公路途中经过市,甲车从市到市,乙车从市到市,甲车的速度比乙车的速度慢,两车距离市的路程与行驶的时间的函数图象如图所示,结合图象信息,解答下列问题:
甲车的速度是______, ______;
求图象中线段所在直线的函数解析式不需要写出自变量的取值范围;
直接写出甲车出发后几小时,两车距市的路程之和是千米.
22.本小题分
如图,一次函数的图象与反比例函数的图象交于,,与轴交于点,与轴交于点.
求反比例函数和一次函数解析式;
直接写出不等式的解集为______;
点在轴上,若,则点的坐标为______.
23.本小题分
【教材呈现】
下面是华师版九年级上册数学教材第页的部分内容.
例如图,在中,、分别是边、的中点,、相交于点.
求证:.
证明:连结.
请根据教材提示,结合图,写出完整的证明过程;
【结论应用】
如图,在中,点、分别是边、的中点,、相交于点,交于点,则 ______;
如图,在中,、分别是边、的中点,过点的直线分别交、于点、,若,,四边形的面积为,则 ______.
24.本小题分
如图,在中,,,点在边上运动,点关于点的对称点为点,以为边在上方作正方形设.
的长为______;
求线段的长用含的代数式表示;
当正方形与重叠部分的图形为四边形时,求的取值范围;
连结,当所在直线将正方形的面积分成:两部分时,直接写出的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.:
14.
15.解:,,,
,
,
,;
.
,
.
16.解:原式
,
当时,原式.
17.解:设每个商品的定价是元,,
由题意,得 ,
整理,得 ,
解得,符合题意.
则元,
答:应涨价元,商店可获利元.
18.,;
等级的人数:人,
补全条形统计图如图:
;
人,
答:估计成绩在分以上含分的学生人数为人.
19.解:如图,点即为所求;
如图,点即为所求;
如图,点即为所求;
20.证明:,,
,
,
,
,
∽.
解:由可知:∽,
,,
,
由可知:,
,
∽,
,
,
.
21.;;
设线段所在直线的解析式为 .
把点,代入,
得:,
解得:.
线段所在直线的函数解析式为;
,
小时,
或,
解得,
答:甲车出发小时或小时时,两车距市的路程之和是千米.
22.将代入反比例函数,
得,解得,
反比例函数的解析式为,
把代入反比例函数,可得:,
解得,
,
将,代入一次函数,
可得,解得,
一次函数的解析式为;
或;
,,
,
,
点在轴上,
设点,
则,
,
,
,
或,
点的坐标为或,
23.【教材呈现】证明:连接,如图,
、分别为、的中点,
为的中位线,
,,
∽,
,
,
即;
【结论应用】、分别是边、的中点,
,,
,
∽,
,
,
同理可得,,
.
如图,作交的延长线于点,交于点,
,,
,
,
,
∽,
,
,
,,
,
,
,
∽,
,
,
∽,
,
,
,
,
,
,
,
,,
,
,
24.;
点关于点的对称点为点,且,
分两种情况:
当时,;
当时,;
当点落在上时,如图,
,
四边形是正方形,且,
,
,
即,
解得:,
当时,正方形与重叠部分的图形为四边形;
当点落在上时,如图,
,
即,
解得:,
当时,正方形与重叠部分的图形为四边形;
综上所述,当和当时,正方形与重叠部分的图形为四边形;
的值是或.
理由:
分两种情况:
当点在边上时,,如图,
,
∽,
,即,
,
,
所在直线将正方形的面积分成:两部分,
或,
或,
解得:,大于,舍去;
.
当在的延长线上时,此时,如图,
由图可知:,,
所在直线将正方形的面积分成:两部分,
::或:,
或,
解得:,小于,舍去,
.
综上所述,的值是或.
第1页,共1页
同课章节目录
