11.1.1平方根课件(共24张PPT)2024-2025学年度八年级上册华师大版数学
文档属性
| 名称 | 11.1.1平方根课件(共24张PPT)2024-2025学年度八年级上册华师大版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 885.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 15:01:45 | ||
图片预览








文档简介
(共24张PPT)
11.1.1 平方根
八年级上
华师版
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.理解平方根、算术平方根的概念,会用根号表示数的平方根、算术平方根.
2. 会求某些数的平方根、算术平方根.
3.会用计算器求一个非负数的算术平方根.
学习目标
重点
重点
新课引入
( )2=25.
5
问题1:已知一幅正方形的油画的面积是25cm2,这幅油画的边长是多少?
注意:-5的平方虽然也是25,但是边长不可以取负数,所得舍去
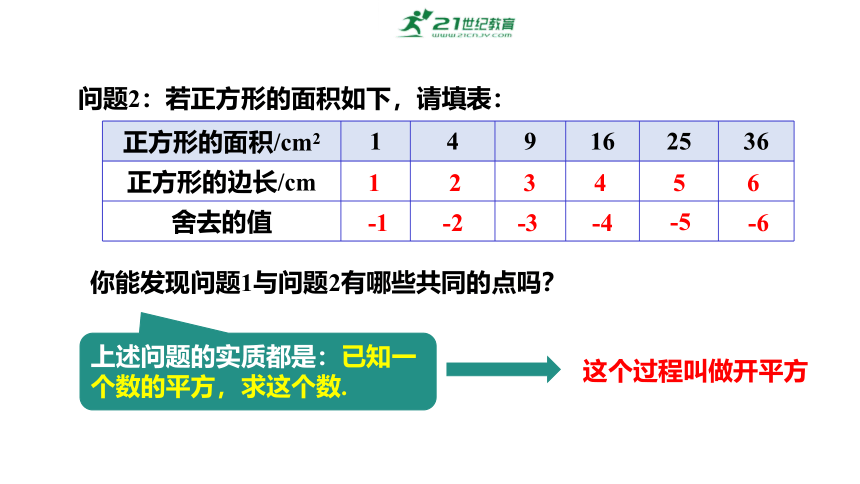
问题2:若正方形的面积如下,请填表:
正方形的面积/cm2 1 4 9 16 25 36
正方形的边长/cm
舍去的值
1
2
3
4
5
6
你能发现问题1与问题2有哪些共同的点吗?
上述问题的实质都是:已知一个数的平方,求这个数.
-1
-2
-3
-4
-5
-6
这个过程叫做开平方
如果一个数的平方等于 a,即 x2 = a,那么这个数叫做 a 的平方根.
例:5 的平方等于 25,所以 5 叫做 25 的平方根.
25的平方根只有一个吗?还有没有别的数的平方也等于25?
新知学习
在问题1中,因为52=25,所以5是25的平方根.
又因为(-5)2=25,所以-5也是25的一个平方根.
通过问题2我们发现,正数的平方根应该都有____个,而且互为______数
2
相反
例1 求 100 的平方根.
解: 因为 102 = 100,(-10)2 = 100,
除了 10 和 -10 以外,任何数的平方都不等于 100,
所以 100 的平方根是 10 和 -10.
也可以说,100 的平方根是 ±10.
试一试
(1) 144 的平方根是什么?
(2) 0 的平方根是什么?
(3) -4 有没有平方根?为什么?
±12
0
-4 没有平方根,因为任何数的平方都不等于负数.
思考
通过这些题目的解答,你能发现什么 请你自己也编三道求平方根的题目,并给出解答.
编题:
(1) 64 的平方根是什么?
(2) 625 的平方根是什么?
(3) -81 有没有平方根?为什么?
±8
±25
-81 没有平方根,因为任何数的平方都不等于负数.
平方根的性质:
1.正数有两个平方根,两个平方根互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
归纳
二 算术平方根
一个正数如果有平方根,那么必定有两个,它们互为相反数.
正数 a 的正的平方根,叫做 a 的算术平方根,记作 ,读作“根号 a”;另一个平方根是它的相反数,即 . 因此,正数a的平方根可以记作 ,其中a称为被开方数.
概括
特殊:0 的算术平方根是 0. 记作 .
根号
被开方数
(a是非负数,a≥0)
根指数
根指数为2时,省略不写
例2.下列说法错误的是 ( )
A. 5 是 25 的算术平方根
B. 0 的平方根与算术平方根都是 0
C. -1 没有平方根
D. 1 的平方根是 1
D
例3.下列说法正确的是( )
A. -5 是 25 的平方根
B. 25 的平方根是 -5
C. -5 是 (-5)2 的算术平方根
D. ±5 是 (-5)2 的算术平方根
A
3.一个正数 x 的两个平方根是 2a - 3 与 5 - a,则 x 的值是( )
A. 49 B. 36
C. 64 D. 81
A
针对训练
1.一个正数 x 的两个平方根是 2a - 3 与 5 - a,则 x 的值是( )
A. 49 B. 36
C. 64 D. 81
A
求一个非负数的平方根的运算,叫做开平方.
思考
平方与开平方有什么关系?
平方与开平方互为逆运算
三 开平方运算
解:(1)因为72 =49,所以 ,因此49的平方根为 .
(1)49; (2) .
例5 将下列各数开平方:
(2)因为 ,所以 ,因此 的平方根为 .
例6.将下列各数开平方:
(1)225; (2)52;
解:(1)因为152 =225,所以 ,
因此225的平方根为 .
(2)因为52 =25,所以25的平方根为 .
(3) .
(3)因为 ,所以 ,
因此 的平方根为 .
四 用计算器求算术平方根
将2016开平方运算的结果是多少?如何计算呢?
思考
对于较大的数,或无法直接找到平方等于某个数时,可以借助计算器来求一个数的算术平方根(有时会是近似值).
在计算器上依次键入: .
被开方数
=
计算器计算算术平方根的方法:
例7 用计算器求下列各数的算术平方根:
说明:用计算器求一个正数的算术平方根,只需直接按书写顺序按键即可.
解:(1)在计算器上依次键入: ,
显示结果为23,所以529的算术平方根为:
5
2
9
=
(2)在计算器上依次键入:
显示结果为 6.6940271884718 ,要求精确到0.01,可得
4
4
.
8
1
=
(1)529 ; (2)44.81(精确到0.01).
例8. 用计算器求下列各数的算术平方根:(结果精确到小数点后两位)
(1)0.0206; (2)407; (3)6800.
解:(1)
(2)
(3)
随堂练习
1. 已知a,b,c满足 +(b+2)2+|c-3|=0,分别求出a,b,c的值.
具有非负性,每一项都必须为0
解:∵ +(b+2)2+|c-3|=0,
∴ =0,(b+2)2=0,|c-3|=0,
∴a-2=0,b+2=0,c-3=0,
解得a=2,b=-2,c=3.
2.(1) 在哪两个相邻的整数之间?
(2)3.1< <3.2正确吗?
(3)下列四个结论中,正确的是( )
A. 3.15< <3.16 B. 3.16< <3.17
C. 3.17< <3.18 D. 3.18< <3.19
在3和4之间.
正确.
B
性质
算术平方根
概念
一个数的平方等于a,这个数叫做a的平方根.
①一个正数的平方根有两个,它们互为相反数.
②0的平方根还是0.
③负数没有平方根.
正数a的正的平方根叫做a的算术平方根
平方根
用计算器求一个数的算术平方根
课堂小结
11.1.1 平方根
八年级上
华师版
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.理解平方根、算术平方根的概念,会用根号表示数的平方根、算术平方根.
2. 会求某些数的平方根、算术平方根.
3.会用计算器求一个非负数的算术平方根.
学习目标
重点
重点
新课引入
( )2=25.
5
问题1:已知一幅正方形的油画的面积是25cm2,这幅油画的边长是多少?
注意:-5的平方虽然也是25,但是边长不可以取负数,所得舍去
问题2:若正方形的面积如下,请填表:
正方形的面积/cm2 1 4 9 16 25 36
正方形的边长/cm
舍去的值
1
2
3
4
5
6
你能发现问题1与问题2有哪些共同的点吗?
上述问题的实质都是:已知一个数的平方,求这个数.
-1
-2
-3
-4
-5
-6
这个过程叫做开平方
如果一个数的平方等于 a,即 x2 = a,那么这个数叫做 a 的平方根.
例:5 的平方等于 25,所以 5 叫做 25 的平方根.
25的平方根只有一个吗?还有没有别的数的平方也等于25?
新知学习
在问题1中,因为52=25,所以5是25的平方根.
又因为(-5)2=25,所以-5也是25的一个平方根.
通过问题2我们发现,正数的平方根应该都有____个,而且互为______数
2
相反
例1 求 100 的平方根.
解: 因为 102 = 100,(-10)2 = 100,
除了 10 和 -10 以外,任何数的平方都不等于 100,
所以 100 的平方根是 10 和 -10.
也可以说,100 的平方根是 ±10.
试一试
(1) 144 的平方根是什么?
(2) 0 的平方根是什么?
(3) -4 有没有平方根?为什么?
±12
0
-4 没有平方根,因为任何数的平方都不等于负数.
思考
通过这些题目的解答,你能发现什么 请你自己也编三道求平方根的题目,并给出解答.
编题:
(1) 64 的平方根是什么?
(2) 625 的平方根是什么?
(3) -81 有没有平方根?为什么?
±8
±25
-81 没有平方根,因为任何数的平方都不等于负数.
平方根的性质:
1.正数有两个平方根,两个平方根互为相反数.
2.0的平方根还是0.
3.负数没有平方根.
归纳
二 算术平方根
一个正数如果有平方根,那么必定有两个,它们互为相反数.
正数 a 的正的平方根,叫做 a 的算术平方根,记作 ,读作“根号 a”;另一个平方根是它的相反数,即 . 因此,正数a的平方根可以记作 ,其中a称为被开方数.
概括
特殊:0 的算术平方根是 0. 记作 .
根号
被开方数
(a是非负数,a≥0)
根指数
根指数为2时,省略不写
例2.下列说法错误的是 ( )
A. 5 是 25 的算术平方根
B. 0 的平方根与算术平方根都是 0
C. -1 没有平方根
D. 1 的平方根是 1
D
例3.下列说法正确的是( )
A. -5 是 25 的平方根
B. 25 的平方根是 -5
C. -5 是 (-5)2 的算术平方根
D. ±5 是 (-5)2 的算术平方根
A
3.一个正数 x 的两个平方根是 2a - 3 与 5 - a,则 x 的值是( )
A. 49 B. 36
C. 64 D. 81
A
针对训练
1.一个正数 x 的两个平方根是 2a - 3 与 5 - a,则 x 的值是( )
A. 49 B. 36
C. 64 D. 81
A
求一个非负数的平方根的运算,叫做开平方.
思考
平方与开平方有什么关系?
平方与开平方互为逆运算
三 开平方运算
解:(1)因为72 =49,所以 ,因此49的平方根为 .
(1)49; (2) .
例5 将下列各数开平方:
(2)因为 ,所以 ,因此 的平方根为 .
例6.将下列各数开平方:
(1)225; (2)52;
解:(1)因为152 =225,所以 ,
因此225的平方根为 .
(2)因为52 =25,所以25的平方根为 .
(3) .
(3)因为 ,所以 ,
因此 的平方根为 .
四 用计算器求算术平方根
将2016开平方运算的结果是多少?如何计算呢?
思考
对于较大的数,或无法直接找到平方等于某个数时,可以借助计算器来求一个数的算术平方根(有时会是近似值).
在计算器上依次键入: .
被开方数
=
计算器计算算术平方根的方法:
例7 用计算器求下列各数的算术平方根:
说明:用计算器求一个正数的算术平方根,只需直接按书写顺序按键即可.
解:(1)在计算器上依次键入: ,
显示结果为23,所以529的算术平方根为:
5
2
9
=
(2)在计算器上依次键入:
显示结果为 6.6940271884718 ,要求精确到0.01,可得
4
4
.
8
1
=
(1)529 ; (2)44.81(精确到0.01).
例8. 用计算器求下列各数的算术平方根:(结果精确到小数点后两位)
(1)0.0206; (2)407; (3)6800.
解:(1)
(2)
(3)
随堂练习
1. 已知a,b,c满足 +(b+2)2+|c-3|=0,分别求出a,b,c的值.
具有非负性,每一项都必须为0
解:∵ +(b+2)2+|c-3|=0,
∴ =0,(b+2)2=0,|c-3|=0,
∴a-2=0,b+2=0,c-3=0,
解得a=2,b=-2,c=3.
2.(1) 在哪两个相邻的整数之间?
(2)3.1< <3.2正确吗?
(3)下列四个结论中,正确的是( )
A. 3.15< <3.16 B. 3.16< <3.17
C. 3.17< <3.18 D. 3.18< <3.19
在3和4之间.
正确.
B
性质
算术平方根
概念
一个数的平方等于a,这个数叫做a的平方根.
①一个正数的平方根有两个,它们互为相反数.
②0的平方根还是0.
③负数没有平方根.
正数a的正的平方根叫做a的算术平方根
平方根
用计算器求一个数的算术平方根
课堂小结
