2024-2025学年河南省郑州市郑中国际学校九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年河南省郑州市郑中国际学校九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 66.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 19:58:42 | ||
图片预览



文档简介
2024-2025学年河南省郑州市郑中国际学校九年级(上)开学数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列说法中正确的是( )
A. 有一组邻边相等的四边形是菱形
B. 有一个角是直角的四边形是矩形
C. 有一组邻边相等且有一个角是直角的四边形是正方形
D. 对角线互相平分、垂直且相等的四边形是正方形
2.在 中,对角线、相交于点,若,则下列结论错误的是( )
A. B. C. D.
3.若是关于的一元二次方程,则的值为( )
A. B. C. D.
4.小明在估算方程的解时,列出的部分对应值如下表:
则可判断方程的解的取值范围是( )
A. 或 B. 或
C. 或 D. 或
5.若是一元二次方程的一个实数根,则的值是( )
A. B. C. D.
6.若方程的左边可以写成一个完全平方式,则的值为( )
A. 或 B. C. D. 或
7.若三角形的两边长分别是和,第三边的长是方程的一个根,则这个三角形的周长是( )
A. B. C. 或 D. 或
8.如图,一根木棍,斜靠在与地面垂直的墙上,当木棍端沿墙下滑,且端沿地面向右滑行时,的中点到点的距离( )
A. 变大 B. 变小
C. 先变小后变大 D. 不变
9.如图,四边形是菱形,,,于,则等于( )
A.
B.
C.
D.
10.如图,正方形的对角线,相交于,平分交于,于,交于,则下列结论:;;≌;平分其中正确的结论有( )
A. 个 B. 个
C. 个 D. 个
二、填空题:本题共6小题,每小题3分,共18分。
11.如图,在矩形中,点,分别是,上一点,,只需添加一个条件即可证明四边形为菱形,这个条件可以是 写出一个即可.
12.关于的一元二次方程有实数根,则的取值范围是______.
13.若是一个直角三角形两条直角边的长,,满足,则这个直角三角形的斜边长为______.
14.念奴娇赤壁怀古,在苏轼笔下,周瑜年少有为,文采风流,雄姿英发,谈笑间,樯橹灰飞烟灭,然天妒英才,英年早逝,欣赏下面改编的诗歌,“大江东去浪淘尽,千古风流数人物而立之年督东吴,早逝英年两位数十位恰小个位三,个位平方与寿符”若设这位风流人物去世的年龄十位数字为,则可列方程为______.
15.如图,有一个长方形纸片,,,点为上一点,将纸片沿折叠,的对应边恰好经过点,则线段的长为______.
16.如图,为坐标原点,四边形为矩形,,,点是的中点,点在上运动,当是以为腰的等腰三角形时,则点的坐标为______.
三、解答题:本题共7小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
以配方法解方程:.
以公式法解方程:.
.
.
18.本小题分
已知关于的一元二次方程为常数.
若方程的一个根为,求的值及方程的另一个根;
求证:不论为何值时,方程总有两个不相等的实数根.
19.本小题分
已知关于的一元二次方程有两个实数根设是方程的一个实数根,且满足,求的值.
20.本小题分
下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.
已知:四边形是平行四边形.
求作:菱形点在上,点在上.
作法:以为圆心,长为半径作弧,交于点;
以为圆心,长为半径作弧,交于点;
连接.
所以四边形为所求的菱形.
根据小明设计的尺规作图过程,
使用直尺和圆规,补全图形;保留作图痕迹
完成下面的证明.
证明:,,
____________.
在 中,,
即.
四边形为平行四边形.______填推理的依据
,
四边形为菱形.______填推理的依据
21.本小题分
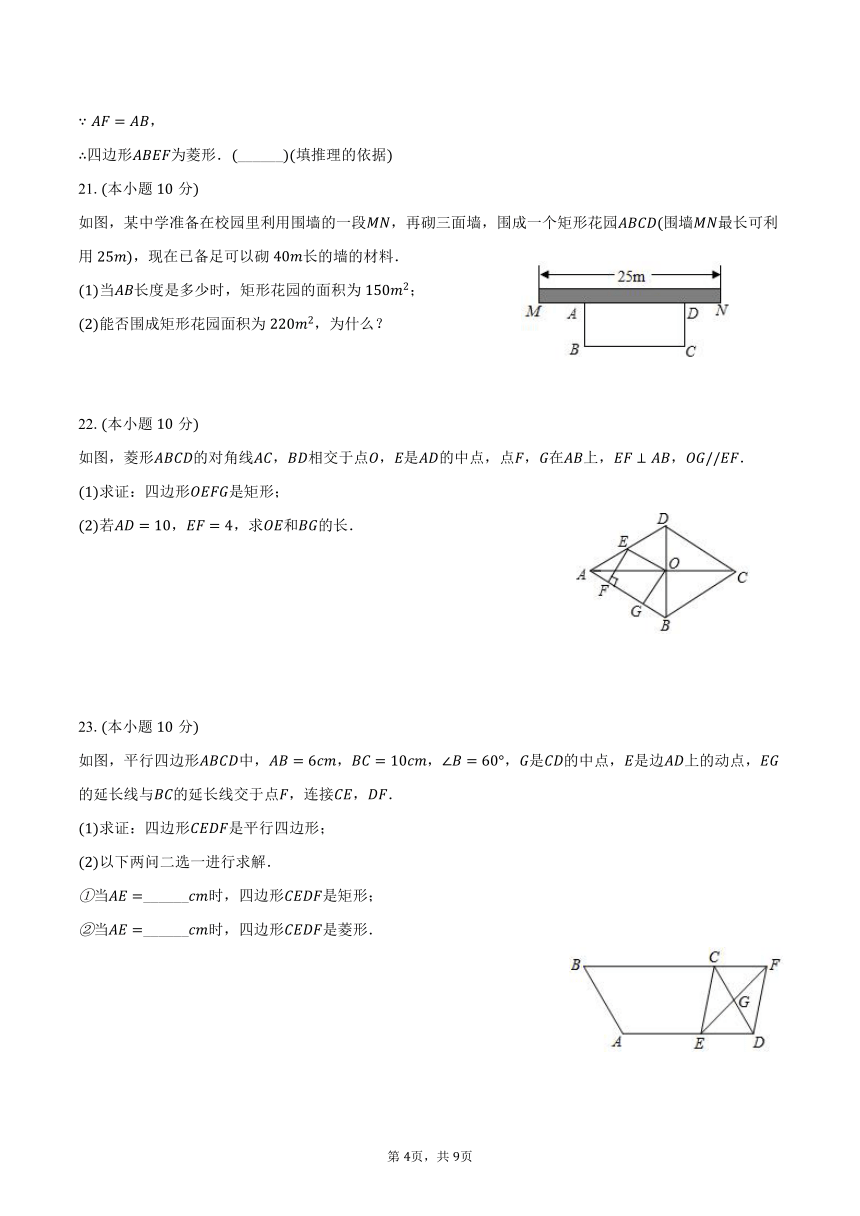
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园围墙最长可利用,现在已备足可以砌长的墙的材料.
当长度是多少时,矩形花园的面积为;
能否围成矩形花园面积为,为什么?
22.本小题分
如图,菱形的对角线,相交于点,是的中点,点,在上,,.
求证:四边形是矩形;
若,,求和的长.
23.本小题分
如图,平行四边形中,,,,是的中点,是边上的动点,的延长线与的延长线交于点,连接,.
求证:四边形是平行四边形;
以下两问二选一进行求解.
当______时,四边形是矩形;
当______时,四边形是菱形.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.且
13.
14.
15.
16.或或
17.解:,
,
,
,
则,
所以.
,
,
,
,
则,
所以.
,
,
,
则或,
所以,.
,
,
,
,
则,
所以.
18.解:把代入方程可得,
解得,
当时,原方程为,
解得,
即方程的另一根为;
,,,
,
不论为何值时,方程总有两个不相等的实数根.
19.解:根据题意得,
解得;
是方程的一个实数根,则,则,
则即,
解得:舍去或.
故的值为.
20.解:菱形即为所求.
证明:,,
,
在 中,,
即.
四边形为平行四边形.一组对边平行且相等的四边形是平行四边形,填推理的依据
,
四边形为菱形.邻边相等的四边形是菱形
21.解:设,则,
依题意得:,
整理得:,
解得:,.
当时,,不合题意,舍去;
当时,,符合题意.
答:当长度是时,矩形花园的面积为.
不能,理由如下:
设,则,
依题意得:,
整理得:.
,
该方程无实数根,
不能围成面积为的矩形花园.
22.解:四边形是菱形,
,
是的中点,
是的中位线,
,
,
四边形是平行四边形,
,
,
平行四边形是矩形;
四边形是菱形,
,,
,
是的中点,
;
由知,四边形是矩形,
,
,,
,
.
23.证明:四边形是平行四边形,
,
,
是的中点,
,
在和中,
,
≌,
,
四边形是平行四边形;
;
.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列说法中正确的是( )
A. 有一组邻边相等的四边形是菱形
B. 有一个角是直角的四边形是矩形
C. 有一组邻边相等且有一个角是直角的四边形是正方形
D. 对角线互相平分、垂直且相等的四边形是正方形
2.在 中,对角线、相交于点,若,则下列结论错误的是( )
A. B. C. D.
3.若是关于的一元二次方程,则的值为( )
A. B. C. D.
4.小明在估算方程的解时,列出的部分对应值如下表:
则可判断方程的解的取值范围是( )
A. 或 B. 或
C. 或 D. 或
5.若是一元二次方程的一个实数根,则的值是( )
A. B. C. D.
6.若方程的左边可以写成一个完全平方式,则的值为( )
A. 或 B. C. D. 或
7.若三角形的两边长分别是和,第三边的长是方程的一个根,则这个三角形的周长是( )
A. B. C. 或 D. 或
8.如图,一根木棍,斜靠在与地面垂直的墙上,当木棍端沿墙下滑,且端沿地面向右滑行时,的中点到点的距离( )
A. 变大 B. 变小
C. 先变小后变大 D. 不变
9.如图,四边形是菱形,,,于,则等于( )
A.
B.
C.
D.
10.如图,正方形的对角线,相交于,平分交于,于,交于,则下列结论:;;≌;平分其中正确的结论有( )
A. 个 B. 个
C. 个 D. 个
二、填空题:本题共6小题,每小题3分,共18分。
11.如图,在矩形中,点,分别是,上一点,,只需添加一个条件即可证明四边形为菱形,这个条件可以是 写出一个即可.
12.关于的一元二次方程有实数根,则的取值范围是______.
13.若是一个直角三角形两条直角边的长,,满足,则这个直角三角形的斜边长为______.
14.念奴娇赤壁怀古,在苏轼笔下,周瑜年少有为,文采风流,雄姿英发,谈笑间,樯橹灰飞烟灭,然天妒英才,英年早逝,欣赏下面改编的诗歌,“大江东去浪淘尽,千古风流数人物而立之年督东吴,早逝英年两位数十位恰小个位三,个位平方与寿符”若设这位风流人物去世的年龄十位数字为,则可列方程为______.
15.如图,有一个长方形纸片,,,点为上一点,将纸片沿折叠,的对应边恰好经过点,则线段的长为______.
16.如图,为坐标原点,四边形为矩形,,,点是的中点,点在上运动,当是以为腰的等腰三角形时,则点的坐标为______.
三、解答题:本题共7小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
以配方法解方程:.
以公式法解方程:.
.
.
18.本小题分
已知关于的一元二次方程为常数.
若方程的一个根为,求的值及方程的另一个根;
求证:不论为何值时,方程总有两个不相等的实数根.
19.本小题分
已知关于的一元二次方程有两个实数根设是方程的一个实数根,且满足,求的值.
20.本小题分
下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.
已知:四边形是平行四边形.
求作:菱形点在上,点在上.
作法:以为圆心,长为半径作弧,交于点;
以为圆心,长为半径作弧,交于点;
连接.
所以四边形为所求的菱形.
根据小明设计的尺规作图过程,
使用直尺和圆规,补全图形;保留作图痕迹
完成下面的证明.
证明:,,
____________.
在 中,,
即.
四边形为平行四边形.______填推理的依据
,
四边形为菱形.______填推理的依据
21.本小题分
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园围墙最长可利用,现在已备足可以砌长的墙的材料.
当长度是多少时,矩形花园的面积为;
能否围成矩形花园面积为,为什么?
22.本小题分
如图,菱形的对角线,相交于点,是的中点,点,在上,,.
求证:四边形是矩形;
若,,求和的长.
23.本小题分
如图,平行四边形中,,,,是的中点,是边上的动点,的延长线与的延长线交于点,连接,.
求证:四边形是平行四边形;
以下两问二选一进行求解.
当______时,四边形是矩形;
当______时,四边形是菱形.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.且
13.
14.
15.
16.或或
17.解:,
,
,
,
则,
所以.
,
,
,
,
则,
所以.
,
,
,
则或,
所以,.
,
,
,
,
则,
所以.
18.解:把代入方程可得,
解得,
当时,原方程为,
解得,
即方程的另一根为;
,,,
,
不论为何值时,方程总有两个不相等的实数根.
19.解:根据题意得,
解得;
是方程的一个实数根,则,则,
则即,
解得:舍去或.
故的值为.
20.解:菱形即为所求.
证明:,,
,
在 中,,
即.
四边形为平行四边形.一组对边平行且相等的四边形是平行四边形,填推理的依据
,
四边形为菱形.邻边相等的四边形是菱形
21.解:设,则,
依题意得:,
整理得:,
解得:,.
当时,,不合题意,舍去;
当时,,符合题意.
答:当长度是时,矩形花园的面积为.
不能,理由如下:
设,则,
依题意得:,
整理得:.
,
该方程无实数根,
不能围成面积为的矩形花园.
22.解:四边形是菱形,
,
是的中点,
是的中位线,
,
,
四边形是平行四边形,
,
,
平行四边形是矩形;
四边形是菱形,
,,
,
是的中点,
;
由知,四边形是矩形,
,
,,
,
.
23.证明:四边形是平行四边形,
,
,
是的中点,
,
在和中,
,
≌,
,
四边形是平行四边形;
;
.
第1页,共1页
同课章节目录
