2024-2025学年广西南宁三中青秀校区九年级(上)开学数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年广西南宁三中青秀校区九年级(上)开学数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 138.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 20:02:05 | ||
图片预览




文档简介
2024-2025学年广西南宁三中青秀校区九年级(上)开学
数学试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.( )
A. B. C. D.
2.我国近年来大力推进国家教育数字化战略行动,截至年月上旬,上线慕课数量超过万门,学习人次达,建设和应用规模居世界第一用科学记数法将数据表示为( )
A. B. C. D.
3.为了解我校初三年级所有同学的数学成绩,从中抽出名同学的数学成绩进行调查,抽出的名考生的数学成绩是( )
A. 总体 B. 样本 C. 个体 D. 样本容量
4.下列计算正确的是( )
A. B.
C. D.
5.不等关系在生活中广泛存在如图,、分别表示两位同学的身高,表示台阶的高度图中两人的对话体现的数学原理是( )
A. 若,则
B. 若,,则
C. 若,,则
D. 若,,则
6.一只杯子静止在斜面上,其受力分析如图所示,重力的方向竖直向下,支持力的方向与斜面垂直,摩擦力的方向与斜面平行若斜面的坡角,则摩擦力与重力方向的夹角的度数为( )
A.
B.
C.
D.
7.如图,在一块长,宽的矩形耕地上挖三条水渠水渠的宽都相等,水渠把耕地分成面积均为平方米的个矩形小块,求水渠宽度设水渠宽,列方程正确的是( )
A. B.
C. D.
8.如图,在中,是边的中点按下列要求作图:以点为圆心、适当长为半径画弧,交线段于点,交于点;以点为圆心、长为半径画弧,交线段于点;以点为圆心、长为半径画弧,交前一条弧于点,点与点在直线同侧;作直线,交于点下列结论不一定成立的是( )
A.
B.
C.
D.
9.如图,数学实践活动课上小明用两根木条钉成一个角形框架,且,,将一根橡皮筋两端固定在点,处,拉展成线段,在平面内,拉动橡皮筋上的一点,当四边形是菱形时,橡皮筋再次被拉长了( )
A.
B.
C.
D.
10.如图,已知矩形纸片,其中,,现将纸片进行如下操作:第一步,如图将纸片对折,使与重合,折痕为,展开后如图;第二步,再将图中的纸片沿对角线折叠,展开后如图;第三步,将图中的纸片沿过点的直线折叠,使点落在对角线上的点处,如图则的长为( )
A. B. C. D.
11.对称轴为直线的抛物线、、为常数,且如图所示,小明同学得出了以下结论:,当时,随的增大而增大,,为任意实数其中结论正确的个数为( )
A.
B.
C.
D.
12.如图,矩形中,为其对角线,一动点从出发,沿着的路径行进,过点作,垂足为设点的运动路程为,为,与的函数图象如图,则的长为( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题2分,共12分。
13.计算:的平方根是 .
14.若等腰三角形的一个底角的度数为,则它的顶角的度数为______
15.若关于的一元二次方程有两个相等的实数根,则的值为______.
16.如图,,分别是边,的中点,连接,若,
,则的长为______.
17.飞机着陆后滑行的距离单位:关于滑行时间单位:的函数解析式是
在飞机着陆滑行中,飞机从开始滑行到停止所需时间为______秒
18.如图,在矩形中,,,,分别是,的中点,的平分线交于点,点是线段上的一个动点,则的周长最小值为______.
三、解答题:本题共7小题,共62分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:.
20.本小题分
解方程:.
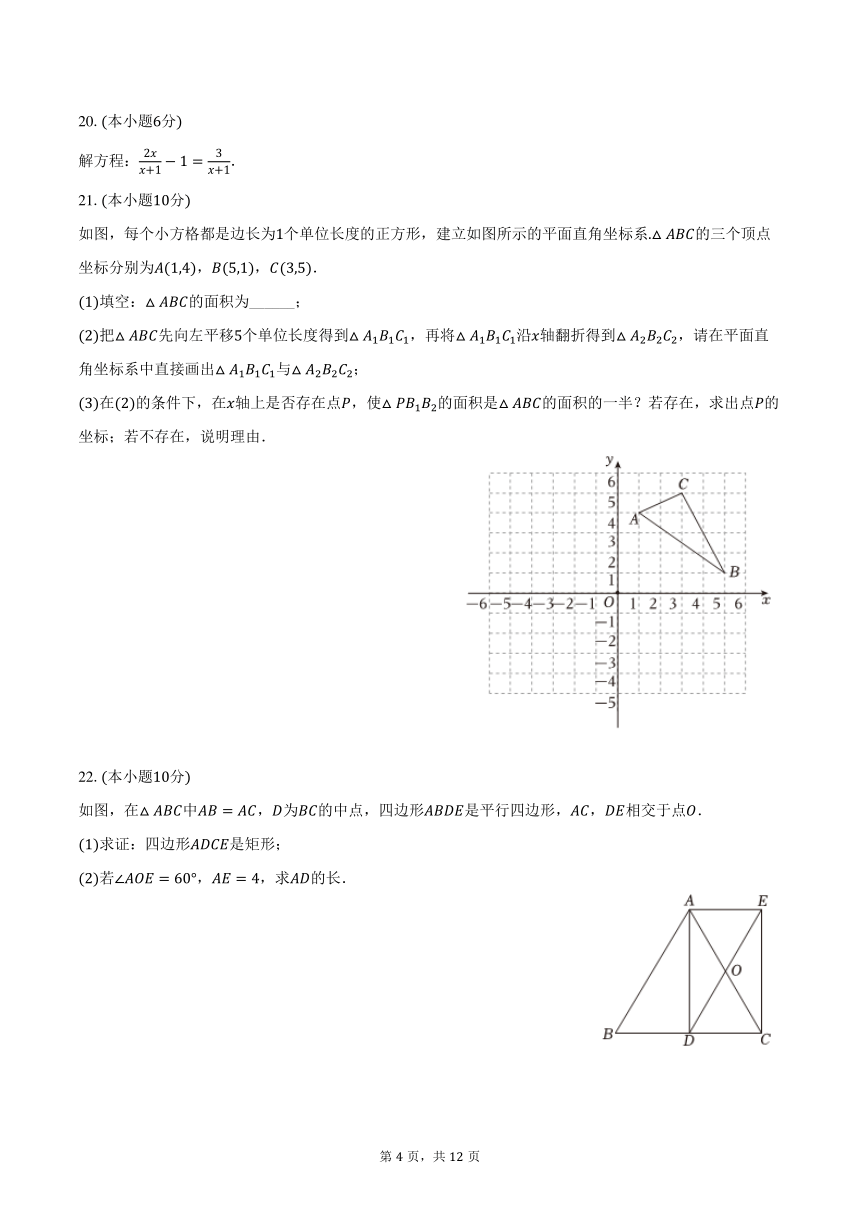
21.本小题分
如图,每个小方格都是边长为个单位长度的正方形,建立如图所示的平面直角坐标系的三个顶点坐标分别为,,.
填空:的面积为______;
把先向左平移个单位长度得到,再将沿轴翻折得到,请在平面直角坐标系中直接画出与;
在的条件下,在轴上是否存在点,使的面积是的面积的一半?若存在,求出点的坐标;若不存在,说明理由.
22.本小题分
如图,在中,为的中点,四边形是平行四边形,,相交于点.
求证:四边形是矩形;
若,,求的长.
23.本小题分
某条东西方向道路双向共有三条车道,在早晚高峰经常会拥堵,数学研究小组希望改善道路拥堵情况,他们对该路段的交通量辆分钟和时间进行了统计和分析,得到下列表格,并发现时间和交通量的变化规律符合一次函数的特征.
时间 时 时 时 时 时
自西向东交通量辆分钟
自东向西交通量辆分钟
请用一次函数分别表示与、与之间的函数关系不写定义域
如图,同学们希望设置可变车道来改善拥堵状况,根据车流量情况改变可变车道的行车方向单位时间内双向交通总量为,车流量大的方向交通量为,经查阅资料得:当,需要使可变车道行车方向与拥堵方向相同,以改善交通情况该路段从时至时,如何设置可变车道行车方向以缓解交通拥堵,并说明理由.
24.本小题分
【课本再现】
如图,正方形的对角线相交于点,点又是正方形的一个顶点,而且这两个正方形的边长都为,四边形为两个正方形重叠部分正方形可绕点转动则下列结论正确的是______填序号即可.
≌;
;
四边形的面积总等于;
连接,总有.
【类比迁移】
如图,矩形的中心是矩形的一个顶点,与边相交于点,与边相交于点,连接,矩形可绕着点旋转,猜想,,之间的数量关系,并进行证明;
【拓展应用】
如图,在中,,,,直角的顶点在边的中点处,它的两条边和分别与直线,相交于点,,可绕着点旋转,当时,求线段的长度.
25.本小题分
如图,抛物线与轴交于,两点,与轴交于点是抛物线上的任意一点不与点重合,点的横坐标为,抛物线上点与点之间的部分包含端点记为图象.
求抛物线的解析式;
若点位于线段上方,求面积的最大值;
若图象的最大值与最小值的差为,求的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.解:原式
.
20.解:在方程两边同乘以,得:
,
解得:,
检验:把代入,得:,
是原分式方程的解.
21..
如图,与即为所求.
设点的坐标为,
的面积是的面积的一半,
,
解得或,
点的坐标为或
22.证明:四边形是平行四边形,
,
为中点,
,
四边形是平行四边形,
,为中点,
,
平行四边形是是矩形;
解:四边形是矩形,
,,
,,
是等边三角形,
,,
,
.
23.解:设、为常数,且.
将,和,代入,
得,
解得,
.
设、为常数,且.
将,和,代入,
得,
解得,
.
.
当时,即,解得;
当时,即,解得.
时到时,可变车道的方向设置为自东向西;时到时,可变车道的方向设置为自西向东.
24.
,理由如下:
连接,延长交于点,连接,
是矩形的中心,
点是的中点.
,
在矩形中,,,
,,
≌,
,,
在矩形中,,
,
在中,
;
设.
当点在线段上时,
,
在中,,
,
,
又由得:,
,
解得.
.
当点在延长线上时,同理可证
,
又在中,.
解得.
故EF的长度为或.
25.解:抛物线与轴交于,两点,
,
解得,
抛物线的解析式为;
解:抛物线的解析式为与轴交于点,
,
设直线的解析式为,
,
解得,
直线的解析式为,
点位于线段上方,
点的横坐标为,
,
过点作轴,交于点,
,
,
,
面积的最大值为;
解:图象的最大值与最小值的差为,
当点在点上方时,
,且,
,
解得或舍去,
,
当点在点下方时,
此时点在点左侧,不满足题意,
点在点右侧,
,
解得或舍去,
综上所述,的取值范围是或.
第1页,共1页
数学试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.( )
A. B. C. D.
2.我国近年来大力推进国家教育数字化战略行动,截至年月上旬,上线慕课数量超过万门,学习人次达,建设和应用规模居世界第一用科学记数法将数据表示为( )
A. B. C. D.
3.为了解我校初三年级所有同学的数学成绩,从中抽出名同学的数学成绩进行调查,抽出的名考生的数学成绩是( )
A. 总体 B. 样本 C. 个体 D. 样本容量
4.下列计算正确的是( )
A. B.
C. D.
5.不等关系在生活中广泛存在如图,、分别表示两位同学的身高,表示台阶的高度图中两人的对话体现的数学原理是( )
A. 若,则
B. 若,,则
C. 若,,则
D. 若,,则
6.一只杯子静止在斜面上,其受力分析如图所示,重力的方向竖直向下,支持力的方向与斜面垂直,摩擦力的方向与斜面平行若斜面的坡角,则摩擦力与重力方向的夹角的度数为( )
A.
B.
C.
D.
7.如图,在一块长,宽的矩形耕地上挖三条水渠水渠的宽都相等,水渠把耕地分成面积均为平方米的个矩形小块,求水渠宽度设水渠宽,列方程正确的是( )
A. B.
C. D.
8.如图,在中,是边的中点按下列要求作图:以点为圆心、适当长为半径画弧,交线段于点,交于点;以点为圆心、长为半径画弧,交线段于点;以点为圆心、长为半径画弧,交前一条弧于点,点与点在直线同侧;作直线,交于点下列结论不一定成立的是( )
A.
B.
C.
D.
9.如图,数学实践活动课上小明用两根木条钉成一个角形框架,且,,将一根橡皮筋两端固定在点,处,拉展成线段,在平面内,拉动橡皮筋上的一点,当四边形是菱形时,橡皮筋再次被拉长了( )
A.
B.
C.
D.
10.如图,已知矩形纸片,其中,,现将纸片进行如下操作:第一步,如图将纸片对折,使与重合,折痕为,展开后如图;第二步,再将图中的纸片沿对角线折叠,展开后如图;第三步,将图中的纸片沿过点的直线折叠,使点落在对角线上的点处,如图则的长为( )
A. B. C. D.
11.对称轴为直线的抛物线、、为常数,且如图所示,小明同学得出了以下结论:,当时,随的增大而增大,,为任意实数其中结论正确的个数为( )
A.
B.
C.
D.
12.如图,矩形中,为其对角线,一动点从出发,沿着的路径行进,过点作,垂足为设点的运动路程为,为,与的函数图象如图,则的长为( )
A.
B.
C.
D.
二、填空题:本题共6小题,每小题2分,共12分。
13.计算:的平方根是 .
14.若等腰三角形的一个底角的度数为,则它的顶角的度数为______
15.若关于的一元二次方程有两个相等的实数根,则的值为______.
16.如图,,分别是边,的中点,连接,若,
,则的长为______.
17.飞机着陆后滑行的距离单位:关于滑行时间单位:的函数解析式是
在飞机着陆滑行中,飞机从开始滑行到停止所需时间为______秒
18.如图,在矩形中,,,,分别是,的中点,的平分线交于点,点是线段上的一个动点,则的周长最小值为______.
三、解答题:本题共7小题,共62分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:.
20.本小题分
解方程:.
21.本小题分
如图,每个小方格都是边长为个单位长度的正方形,建立如图所示的平面直角坐标系的三个顶点坐标分别为,,.
填空:的面积为______;
把先向左平移个单位长度得到,再将沿轴翻折得到,请在平面直角坐标系中直接画出与;
在的条件下,在轴上是否存在点,使的面积是的面积的一半?若存在,求出点的坐标;若不存在,说明理由.
22.本小题分
如图,在中,为的中点,四边形是平行四边形,,相交于点.
求证:四边形是矩形;
若,,求的长.
23.本小题分
某条东西方向道路双向共有三条车道,在早晚高峰经常会拥堵,数学研究小组希望改善道路拥堵情况,他们对该路段的交通量辆分钟和时间进行了统计和分析,得到下列表格,并发现时间和交通量的变化规律符合一次函数的特征.
时间 时 时 时 时 时
自西向东交通量辆分钟
自东向西交通量辆分钟
请用一次函数分别表示与、与之间的函数关系不写定义域
如图,同学们希望设置可变车道来改善拥堵状况,根据车流量情况改变可变车道的行车方向单位时间内双向交通总量为,车流量大的方向交通量为,经查阅资料得:当,需要使可变车道行车方向与拥堵方向相同,以改善交通情况该路段从时至时,如何设置可变车道行车方向以缓解交通拥堵,并说明理由.
24.本小题分
【课本再现】
如图,正方形的对角线相交于点,点又是正方形的一个顶点,而且这两个正方形的边长都为,四边形为两个正方形重叠部分正方形可绕点转动则下列结论正确的是______填序号即可.
≌;
;
四边形的面积总等于;
连接,总有.
【类比迁移】
如图,矩形的中心是矩形的一个顶点,与边相交于点,与边相交于点,连接,矩形可绕着点旋转,猜想,,之间的数量关系,并进行证明;
【拓展应用】
如图,在中,,,,直角的顶点在边的中点处,它的两条边和分别与直线,相交于点,,可绕着点旋转,当时,求线段的长度.
25.本小题分
如图,抛物线与轴交于,两点,与轴交于点是抛物线上的任意一点不与点重合,点的横坐标为,抛物线上点与点之间的部分包含端点记为图象.
求抛物线的解析式;
若点位于线段上方,求面积的最大值;
若图象的最大值与最小值的差为,求的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.解:原式
.
20.解:在方程两边同乘以,得:
,
解得:,
检验:把代入,得:,
是原分式方程的解.
21..
如图,与即为所求.
设点的坐标为,
的面积是的面积的一半,
,
解得或,
点的坐标为或
22.证明:四边形是平行四边形,
,
为中点,
,
四边形是平行四边形,
,为中点,
,
平行四边形是是矩形;
解:四边形是矩形,
,,
,,
是等边三角形,
,,
,
.
23.解:设、为常数,且.
将,和,代入,
得,
解得,
.
设、为常数,且.
将,和,代入,
得,
解得,
.
.
当时,即,解得;
当时,即,解得.
时到时,可变车道的方向设置为自东向西;时到时,可变车道的方向设置为自西向东.
24.
,理由如下:
连接,延长交于点,连接,
是矩形的中心,
点是的中点.
,
在矩形中,,,
,,
≌,
,,
在矩形中,,
,
在中,
;
设.
当点在线段上时,
,
在中,,
,
,
又由得:,
,
解得.
.
当点在延长线上时,同理可证
,
又在中,.
解得.
故EF的长度为或.
25.解:抛物线与轴交于,两点,
,
解得,
抛物线的解析式为;
解:抛物线的解析式为与轴交于点,
,
设直线的解析式为,
,
解得,
直线的解析式为,
点位于线段上方,
点的横坐标为,
,
过点作轴,交于点,
,
,
,
面积的最大值为;
解:图象的最大值与最小值的差为,
当点在点上方时,
,且,
,
解得或舍去,
,
当点在点下方时,
此时点在点左侧,不满足题意,
点在点右侧,
,
解得或舍去,
综上所述,的取值范围是或.
第1页,共1页
同课章节目录
