11.1整式的乘法课件(20张PPT)2024-2025学年七年级数学上册(沪教版2024)
文档属性
| 名称 | 11.1整式的乘法课件(20张PPT)2024-2025学年七年级数学上册(沪教版2024) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 21:19:37 | ||
图片预览






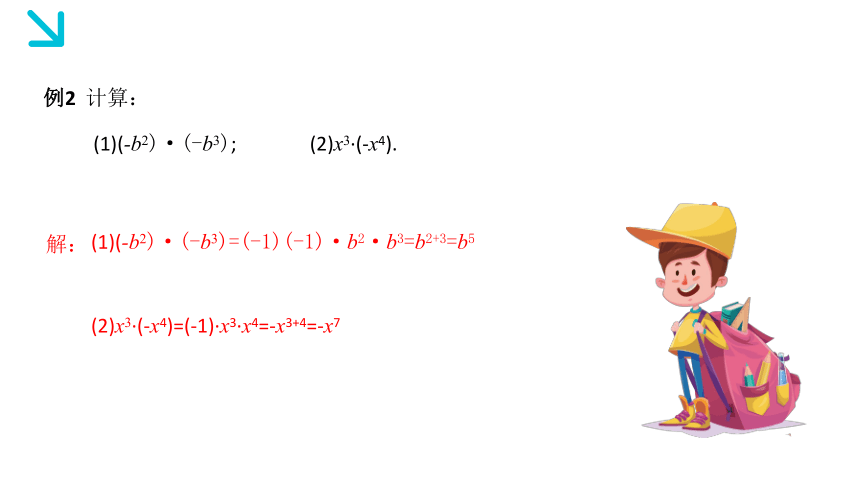


文档简介
(共20张PPT)
11.1 整式的乘法
主讲:
沪教版(2024)七年级数学上册
第11章 整式的乘除
学习目标
目标
1
(1)理解并会进行同底数幂乘法、幂的乘方、积点乘方;
(2)类比数的运算,通过观察和体会、运用幂的意义,最终得到以字母为底数的幂的运算法则。。
重点
2
理解同底数幂、幂的乘方的乘法法则。
难点
3
能运用同底数幂、幂的乘方的乘法法则计算。
新课导入
a·a·a
表示三个a相乘,记作a3,叫作“a的立方”或“a的三次方”.
an
一般地,将n个a相乘的运算叫作乘方,a·a·a·a·……·a·a记作an,乘方的结果叫作幂。在an中,a叫作底数,正整数n叫作指数。an读作“a的n次方”,当an被看作是a的n次方的结果时,也读作“a的n次幂”。
n个a
幂
底数
指数
新课讲授:同底数幂的乘法
22×23=(2×2)×(2×2×2)=2×2×2×2×2=25=22+3
请仿照上面的例子完成下面的等式:
32×34=(3×3)×(3×3×3×3)=3×3×3×3×3×3=36=32+4
(-2)2×(-2)3=[(-2)×(-2)]×[(-2)×(-2)×(-2)]=(-2)×(-2)×(-2)×(-2)×(-2)=(-2)5=(-2)2+3
a2×a3=(a×a)×(a×a×a)=a×a×a×a×a=a5=a2+3
思考与交流
一般地,设m、n是正整数,如何计算am·an?
新课讲授:同底数幂的乘法
am·an
=(a·a·a·……·a·a)·(a·a·a·……·a·a)
=a·a·a·……·a·a
=am+n
m个a
n个a
(乘方的意义)
m+n个a
(乘方的意义)
同底数幂的乘法性质:
am·an=am+n(m、n是正整数)
同底数幂相乘,底数不变,指数相加。
同底数幂的乘法运算
指数的加法运算
典例分析
例1 计算下列各式,结果用幂的形式表示:
解:
(1)102×103;
(2)(-)4×(-)5;
(3)a2·a4;
(4)(a-b)·(a-b)3;
(5)y·y2·y3.
(1)102×103=102+3=105
(2)(-)4×(-)5=(-)4+5=(-)9
(3)a2·a4=a2+4=a6
(4)(a-b)·(a-b)3=(a-b)1+3=(a-b)4
(5)y·y2·y3=y1+2+3=y6
一般地,
am·an·ap=am+n+p
(m、n、p都是正整数)
典例分析
例2 计算:
解:
(1)(-b2)·(-b3); (2)x3·(-x4).
(1)(-b2)·(-b3)=(-1)(-1)·b2·b3=b2+3=b5
(2)x3·(-x4)=(-1)·x3·x4=-x3+4=-x7
学以致用
1. 下列计算是否正确?若不正确,应该如何改正?
(2)x2+x2=x4.
(1)x4·x=x4;
解:
(1)不正确,x4·x=x5.
(2)不正确,x2+x2=2x2.
学以致用
2. 计算下列各式,结果用幂的形式表示:
解:
(1)84×83;
(2)(-10)4×(-10)3;
(3)(-)5×(-)3;
(4)-x·x2·x4;
(5)(x+y)3×(x+y)5;
(6)(-a3)·(-a2)·a4.
(1)84×83=84+3=87
(2)(-10)4×(-10)3=(-10)4+3=(-10)7
(3)(-)5×(-)3=(-)5+3=(-)8
(4)-x·x2·x4;=(-1)·x·x2·x4=-x1+2+4=-x7
(5)(x+y)3×(x+y)5=(x+y)3+5=(x+y)8
(6)(-a3)·(-a2)·a4=(-1)×(-1)·a3·a2·a4=a3+2+4=a9
学以致用
3. 计算:
解:
(1)a2·(-a)2-a3·a;
(2)a3·(-a)2+a·(-a)4;
(1)a2·(-a)2-a3·a
=a2·a2-a3·a
=a2+2-a3+1
=0
(2)a3·(-a)2+a·(-a)4;
=a3·a2+a·a4
=a2+3+a1+4
=2a5
新课讲授:幂的乘方
观察
(23)2=23×23=23+3=23×2
(a3)2=a3·a3=a3+3=a3×2
(am)2=am·am=am+m=a2m(m是正整数)
一般地,设m、n是正整数,如何计算(am)n
新课讲授:幂的乘方
(am)n=am·am·……·am
=am+m+……+m
=amn
n个am
n个m
(乘方的意义)
(同底数幂的乘法性质)
幂的乘方性质:
(am)n=amn(m、n是正整数)
幂的乘方,底数不变,指数相乘。
典例分析
例3 计算下列各式,结果用幂的形式表示:
(1)(102)3;
(2)(a3)4;
(3)[(-b)3]3;
(4)[(a+b)5]3;
解:
(1)(102)3=102×3=106
(2)(a3)4=a3×4=a12
(3)[(-b)3]3=(-b)3×3=(-b)9
(4)[(a+b)5]3=(a+b)5×3=(a+b)15
典例分析
例4 计算:
解:
(1)(a3)4·(a4)3·a
(2)(x3)2·(x3)5
(1)(a3)4·(a4)3·a
=a3×4·a3×4·a1
=a12·a12·a1
=a12+12+1
=a25
(2)(x3)2·(x3)5
=x6·x15
=x21
典例分析
例5 计算:
(1)(a2)3+a2·a3;
(2)m+2m+3m+m·m2·m3-(m2)3
解:
(1)(a2)3+a2·a3
=a2×3+a2+3
=a6+a5
(2)m+2m+3m+m·m2·m3-(m2)3
=6m+m1+2+3-m2×3
=6m+m6-m6
=6m
课堂小结
1
一般地,将n个a相乘的运算叫作乘方,a·a·a·a·……·a·a记作an,乘方的结果叫作幂。在an中,a叫作底数,正整数n叫作指数。an读作“a的n次方”,当an被看作是a的n次方的结果时,也读作“a的n次幂”。
2
同底数幂的乘法性质:
am·an=am+n(m、n是正整数)
同底数幂相乘,底数不变,指数相加。
3
幂的乘方性质:
(am)n=amn(m、n是正整数)
幂的乘方,底数不变,指数相乘。
学以致用
基础巩固题
1.下列计算是否正确?若不正确,应该如何改正?
解:
(1)(a5)2=a7
(2)a5·a2=a10
(1)不正确,(a5)2=a10
(2)不正确,a5·a2=a7
学以致用
基础巩固题
2.计算下列各式,结果用幂的形式表示:
(1)(x4)3·x2;
(2)-(x3)5·(-x3);
(3)y3·(y2)3·(y3)2;
(4)(-x)·[(-x)2]3;
(5)[(x-y)3]2;
(6)[(a+1)3]4·(a+1)3.
解:
(1)(x4)3·x2=x12·x2=x14
(2)-(x3)5·(-x3)=-x15·(-x3)=x18
(3)y3·(y2)3·(y3)2=y3·y6·y6=y12
(4)(-x)·[(-x)2]3=(-x)·(x2)3=(-x)·x6=-x7
(5)[(x-y)3]2=(x-y)6
(6)[(a+1)3]4·(a+1)3=(a+1)12·(a+1)3=(a+1)15
学以致用
基础巩固题
3.随着科技的发展,纳米技术的运用越来越广泛。1米=109纳米,那么1米2= 纳米2.
解:
1米=109纳米
1米2=(109)2纳米2=1018纳米2
1018
主讲:
沪教版(2024)七年级数学上册
感谢聆听
11.1 整式的乘法
主讲:
沪教版(2024)七年级数学上册
第11章 整式的乘除
学习目标
目标
1
(1)理解并会进行同底数幂乘法、幂的乘方、积点乘方;
(2)类比数的运算,通过观察和体会、运用幂的意义,最终得到以字母为底数的幂的运算法则。。
重点
2
理解同底数幂、幂的乘方的乘法法则。
难点
3
能运用同底数幂、幂的乘方的乘法法则计算。
新课导入
a·a·a
表示三个a相乘,记作a3,叫作“a的立方”或“a的三次方”.
an
一般地,将n个a相乘的运算叫作乘方,a·a·a·a·……·a·a记作an,乘方的结果叫作幂。在an中,a叫作底数,正整数n叫作指数。an读作“a的n次方”,当an被看作是a的n次方的结果时,也读作“a的n次幂”。
n个a
幂
底数
指数
新课讲授:同底数幂的乘法
22×23=(2×2)×(2×2×2)=2×2×2×2×2=25=22+3
请仿照上面的例子完成下面的等式:
32×34=(3×3)×(3×3×3×3)=3×3×3×3×3×3=36=32+4
(-2)2×(-2)3=[(-2)×(-2)]×[(-2)×(-2)×(-2)]=(-2)×(-2)×(-2)×(-2)×(-2)=(-2)5=(-2)2+3
a2×a3=(a×a)×(a×a×a)=a×a×a×a×a=a5=a2+3
思考与交流
一般地,设m、n是正整数,如何计算am·an?
新课讲授:同底数幂的乘法
am·an
=(a·a·a·……·a·a)·(a·a·a·……·a·a)
=a·a·a·……·a·a
=am+n
m个a
n个a
(乘方的意义)
m+n个a
(乘方的意义)
同底数幂的乘法性质:
am·an=am+n(m、n是正整数)
同底数幂相乘,底数不变,指数相加。
同底数幂的乘法运算
指数的加法运算
典例分析
例1 计算下列各式,结果用幂的形式表示:
解:
(1)102×103;
(2)(-)4×(-)5;
(3)a2·a4;
(4)(a-b)·(a-b)3;
(5)y·y2·y3.
(1)102×103=102+3=105
(2)(-)4×(-)5=(-)4+5=(-)9
(3)a2·a4=a2+4=a6
(4)(a-b)·(a-b)3=(a-b)1+3=(a-b)4
(5)y·y2·y3=y1+2+3=y6
一般地,
am·an·ap=am+n+p
(m、n、p都是正整数)
典例分析
例2 计算:
解:
(1)(-b2)·(-b3); (2)x3·(-x4).
(1)(-b2)·(-b3)=(-1)(-1)·b2·b3=b2+3=b5
(2)x3·(-x4)=(-1)·x3·x4=-x3+4=-x7
学以致用
1. 下列计算是否正确?若不正确,应该如何改正?
(2)x2+x2=x4.
(1)x4·x=x4;
解:
(1)不正确,x4·x=x5.
(2)不正确,x2+x2=2x2.
学以致用
2. 计算下列各式,结果用幂的形式表示:
解:
(1)84×83;
(2)(-10)4×(-10)3;
(3)(-)5×(-)3;
(4)-x·x2·x4;
(5)(x+y)3×(x+y)5;
(6)(-a3)·(-a2)·a4.
(1)84×83=84+3=87
(2)(-10)4×(-10)3=(-10)4+3=(-10)7
(3)(-)5×(-)3=(-)5+3=(-)8
(4)-x·x2·x4;=(-1)·x·x2·x4=-x1+2+4=-x7
(5)(x+y)3×(x+y)5=(x+y)3+5=(x+y)8
(6)(-a3)·(-a2)·a4=(-1)×(-1)·a3·a2·a4=a3+2+4=a9
学以致用
3. 计算:
解:
(1)a2·(-a)2-a3·a;
(2)a3·(-a)2+a·(-a)4;
(1)a2·(-a)2-a3·a
=a2·a2-a3·a
=a2+2-a3+1
=0
(2)a3·(-a)2+a·(-a)4;
=a3·a2+a·a4
=a2+3+a1+4
=2a5
新课讲授:幂的乘方
观察
(23)2=23×23=23+3=23×2
(a3)2=a3·a3=a3+3=a3×2
(am)2=am·am=am+m=a2m(m是正整数)
一般地,设m、n是正整数,如何计算(am)n
新课讲授:幂的乘方
(am)n=am·am·……·am
=am+m+……+m
=amn
n个am
n个m
(乘方的意义)
(同底数幂的乘法性质)
幂的乘方性质:
(am)n=amn(m、n是正整数)
幂的乘方,底数不变,指数相乘。
典例分析
例3 计算下列各式,结果用幂的形式表示:
(1)(102)3;
(2)(a3)4;
(3)[(-b)3]3;
(4)[(a+b)5]3;
解:
(1)(102)3=102×3=106
(2)(a3)4=a3×4=a12
(3)[(-b)3]3=(-b)3×3=(-b)9
(4)[(a+b)5]3=(a+b)5×3=(a+b)15
典例分析
例4 计算:
解:
(1)(a3)4·(a4)3·a
(2)(x3)2·(x3)5
(1)(a3)4·(a4)3·a
=a3×4·a3×4·a1
=a12·a12·a1
=a12+12+1
=a25
(2)(x3)2·(x3)5
=x6·x15
=x21
典例分析
例5 计算:
(1)(a2)3+a2·a3;
(2)m+2m+3m+m·m2·m3-(m2)3
解:
(1)(a2)3+a2·a3
=a2×3+a2+3
=a6+a5
(2)m+2m+3m+m·m2·m3-(m2)3
=6m+m1+2+3-m2×3
=6m+m6-m6
=6m
课堂小结
1
一般地,将n个a相乘的运算叫作乘方,a·a·a·a·……·a·a记作an,乘方的结果叫作幂。在an中,a叫作底数,正整数n叫作指数。an读作“a的n次方”,当an被看作是a的n次方的结果时,也读作“a的n次幂”。
2
同底数幂的乘法性质:
am·an=am+n(m、n是正整数)
同底数幂相乘,底数不变,指数相加。
3
幂的乘方性质:
(am)n=amn(m、n是正整数)
幂的乘方,底数不变,指数相乘。
学以致用
基础巩固题
1.下列计算是否正确?若不正确,应该如何改正?
解:
(1)(a5)2=a7
(2)a5·a2=a10
(1)不正确,(a5)2=a10
(2)不正确,a5·a2=a7
学以致用
基础巩固题
2.计算下列各式,结果用幂的形式表示:
(1)(x4)3·x2;
(2)-(x3)5·(-x3);
(3)y3·(y2)3·(y3)2;
(4)(-x)·[(-x)2]3;
(5)[(x-y)3]2;
(6)[(a+1)3]4·(a+1)3.
解:
(1)(x4)3·x2=x12·x2=x14
(2)-(x3)5·(-x3)=-x15·(-x3)=x18
(3)y3·(y2)3·(y3)2=y3·y6·y6=y12
(4)(-x)·[(-x)2]3=(-x)·(x2)3=(-x)·x6=-x7
(5)[(x-y)3]2=(x-y)6
(6)[(a+1)3]4·(a+1)3=(a+1)12·(a+1)3=(a+1)15
学以致用
基础巩固题
3.随着科技的发展,纳米技术的运用越来越广泛。1米=109纳米,那么1米2= 纳米2.
解:
1米=109纳米
1米2=(109)2纳米2=1018纳米2
1018
主讲:
沪教版(2024)七年级数学上册
感谢聆听
同课章节目录
