3.1.1 基本计数原理 教学课件(共46张PPT) 高中数学人教B版(2019)选择性必修第二册
文档属性
| 名称 | 3.1.1 基本计数原理 教学课件(共46张PPT) 高中数学人教B版(2019)选择性必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 00:00:00 | ||
图片预览











文档简介
(共46张PPT)
第三章 排列、组合与二项式定理
人教B版(2019)
3.1.1 基本计数原理
课标要点 核心素养
1.了解分类加法计数原理及其意义 数学抽象
2.了解分步乘法计数原理及其意义 数学抽象
3.能利用计数原理解决简单的实际问题 数学运算
情境与问题
在数学学习和日常生活中,我们经常会遇到类似“共有多少种情况”的计数问题. 例如:
(1)一个由 3 个元素组成的集合,共有多少个不同的子集?
(2)由 3 个数字组成的密码锁,如图所示,如果忘记了密码,最多要试多少次才能打开密码锁?
(3)有 4 位同学和 1 位老师站成一排照相,如果老师要站在正中间,如图所示,则有多少种不同的站法?
尝试与发现
你能解答下述两个问题吗?试着由此归纳出一般的规律.
(1)已知某天从北京到上海的 G 字头列车有 43 班,D 字头列车有 2 班,其他列车有 3 班,小张想在这一天坐火车从北京到上海旅游,不考虑其他因素,小张有多少种不同的选择?
(2)从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船. 假定火车每日有 1 班,汽车每日有 3 班,轮船每日有 2 班,那么一天中从甲地到乙地有多少种不同的走法呢?
尝试与发现中的问题(1),小张乘坐的列车可以分为 3 类,即 G 字头列车、 D 字头列车或其他列车,其中任何一类的任何一班车都可以让小张从北京到达上海,因此不同的选择有 43+2+3=48 种.
类似地,问题(2)中,从甲地到乙地,可乘坐三类交通工具:火车、汽车或轮船,每类交通工具又各有若干个班次,选择其中任何一类的任何一个班次都可以从甲地到达乙地,因此一天中不同的走法有 种.
1+3+2=6
1.分类加法计数原理
例 1 在某设计活动中,李明要用红色和蓝色填涂四个格子(如图所示),要求每种颜色都用两次,李明共有多少种不同的填涂方法?
尝试与发现
试给出一种满足条件的涂法,在明确要完成的事情是什么的前提下思考:
(1)怎样用符号表示填涂结果?
(2) 可以将填涂结果分类吗?
3+3=6
尝试与发现
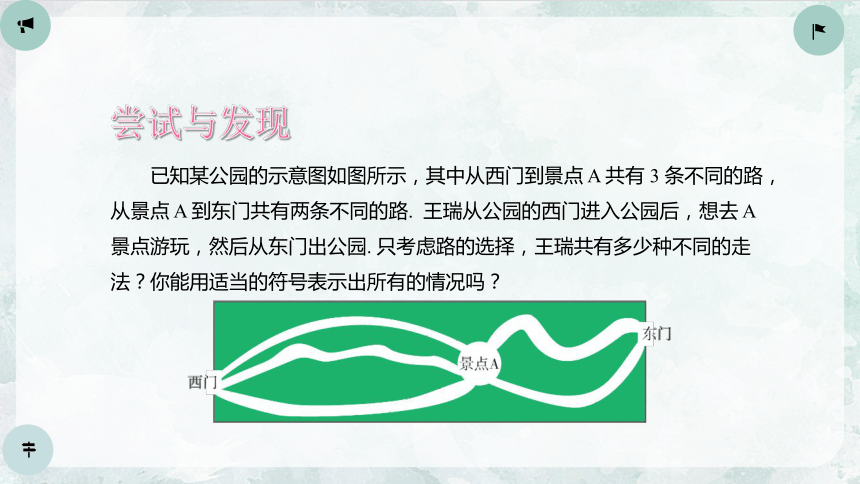
已知某公园的示意图如图所示,其中从西门到景点 A 共有 3 条不同的路,从景点 A 到东门共有两条不同的路. 王瑞从公园的西门进入公园后,想去 A 景点游玩,然后从东门出公园. 只考虑路的选择,王瑞共有多少种不同的走法?你能用适当的符号表示出所有的情况吗?
2.分步乘法计数原理
例2 用 1,2,3,4,5 可以排成多少个数字不重复的三位数?
分析:要排成一个三位数,只需分别指定这个三位数的百位、十位、个位上的数字即可,因此可以分为三步完成.
解:排成一个三位数,可以分为三步:
第一步,确定百位上的数字,共有 5 种方法;
第二步,确定十位上的数字,因为数字不能重复,所以不能是百位上已有的数字,共有 4 种方法;
第三步,确定个位上的数字,共有 3 种方法.
依据分步乘法计数原理,可以排成数字不重复的三位数的个数为5×4×3=60.
分类加法计数原理和分步乘法计数原理合称为基本计数原理.
3.基本计数原理的应用
例3 某班班委由 2 位女同学、3 位男同学组成,现要从该班班委里选出 2 人去参加学校组织的培训活动,要求至少要有 1 位女同学参加,则不同的选法共有多少种?
1+6=7
解:按照选择的女同学人数分为两种情况,即 2 位都是女同学和只有 1 位女同学.
2 位都是女同学的选法显然只有 1 种.
只有 1 位女同学的选法,可以分为两步完成:先从 2 位女同学中选出 1 人,有 2 种选法;再从 3 位男同学中选出 1 人,有 3 种选法。依据分步乘法计数原理,共有不同的选法 2×3=6 种.
依据分类加法计数原理,不同的选法共有 种.
练习提升
B
D
C
C
D
C
C
B
7
40
20
课堂小结:
1.分类加法计数原理
2.分步乘法计数原理
3.基本计数原理的应用
谢谢观看
第三章 排列、组合与二项式定理
人教B版(2019)
3.1.1 基本计数原理
课标要点 核心素养
1.了解分类加法计数原理及其意义 数学抽象
2.了解分步乘法计数原理及其意义 数学抽象
3.能利用计数原理解决简单的实际问题 数学运算
情境与问题
在数学学习和日常生活中,我们经常会遇到类似“共有多少种情况”的计数问题. 例如:
(1)一个由 3 个元素组成的集合,共有多少个不同的子集?
(2)由 3 个数字组成的密码锁,如图所示,如果忘记了密码,最多要试多少次才能打开密码锁?
(3)有 4 位同学和 1 位老师站成一排照相,如果老师要站在正中间,如图所示,则有多少种不同的站法?
尝试与发现
你能解答下述两个问题吗?试着由此归纳出一般的规律.
(1)已知某天从北京到上海的 G 字头列车有 43 班,D 字头列车有 2 班,其他列车有 3 班,小张想在这一天坐火车从北京到上海旅游,不考虑其他因素,小张有多少种不同的选择?
(2)从甲地到乙地,可以乘火车,也可以乘汽车,还可以乘轮船. 假定火车每日有 1 班,汽车每日有 3 班,轮船每日有 2 班,那么一天中从甲地到乙地有多少种不同的走法呢?
尝试与发现中的问题(1),小张乘坐的列车可以分为 3 类,即 G 字头列车、 D 字头列车或其他列车,其中任何一类的任何一班车都可以让小张从北京到达上海,因此不同的选择有 43+2+3=48 种.
类似地,问题(2)中,从甲地到乙地,可乘坐三类交通工具:火车、汽车或轮船,每类交通工具又各有若干个班次,选择其中任何一类的任何一个班次都可以从甲地到达乙地,因此一天中不同的走法有 种.
1+3+2=6
1.分类加法计数原理
例 1 在某设计活动中,李明要用红色和蓝色填涂四个格子(如图所示),要求每种颜色都用两次,李明共有多少种不同的填涂方法?
尝试与发现
试给出一种满足条件的涂法,在明确要完成的事情是什么的前提下思考:
(1)怎样用符号表示填涂结果?
(2) 可以将填涂结果分类吗?
3+3=6
尝试与发现
已知某公园的示意图如图所示,其中从西门到景点 A 共有 3 条不同的路,从景点 A 到东门共有两条不同的路. 王瑞从公园的西门进入公园后,想去 A 景点游玩,然后从东门出公园. 只考虑路的选择,王瑞共有多少种不同的走法?你能用适当的符号表示出所有的情况吗?
2.分步乘法计数原理
例2 用 1,2,3,4,5 可以排成多少个数字不重复的三位数?
分析:要排成一个三位数,只需分别指定这个三位数的百位、十位、个位上的数字即可,因此可以分为三步完成.
解:排成一个三位数,可以分为三步:
第一步,确定百位上的数字,共有 5 种方法;
第二步,确定十位上的数字,因为数字不能重复,所以不能是百位上已有的数字,共有 4 种方法;
第三步,确定个位上的数字,共有 3 种方法.
依据分步乘法计数原理,可以排成数字不重复的三位数的个数为5×4×3=60.
分类加法计数原理和分步乘法计数原理合称为基本计数原理.
3.基本计数原理的应用
例3 某班班委由 2 位女同学、3 位男同学组成,现要从该班班委里选出 2 人去参加学校组织的培训活动,要求至少要有 1 位女同学参加,则不同的选法共有多少种?
1+6=7
解:按照选择的女同学人数分为两种情况,即 2 位都是女同学和只有 1 位女同学.
2 位都是女同学的选法显然只有 1 种.
只有 1 位女同学的选法,可以分为两步完成:先从 2 位女同学中选出 1 人,有 2 种选法;再从 3 位男同学中选出 1 人,有 3 种选法。依据分步乘法计数原理,共有不同的选法 2×3=6 种.
依据分类加法计数原理,不同的选法共有 种.
练习提升
B
D
C
C
D
C
C
B
7
40
20
课堂小结:
1.分类加法计数原理
2.分步乘法计数原理
3.基本计数原理的应用
谢谢观看
