人教版四年级下册数学鸡兔同笼课件(共17张PPT)
文档属性
| 名称 | 人教版四年级下册数学鸡兔同笼课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-31 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
难点:用假设法解决鸡兔同笼问题
数学广角--
历史激趣,揭示课题
我国古代数学名著《孙子算经》中记载了一道
数学趣题——“鸡兔同笼”问题 。
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
说一说:从题中你了解到哪些信息?
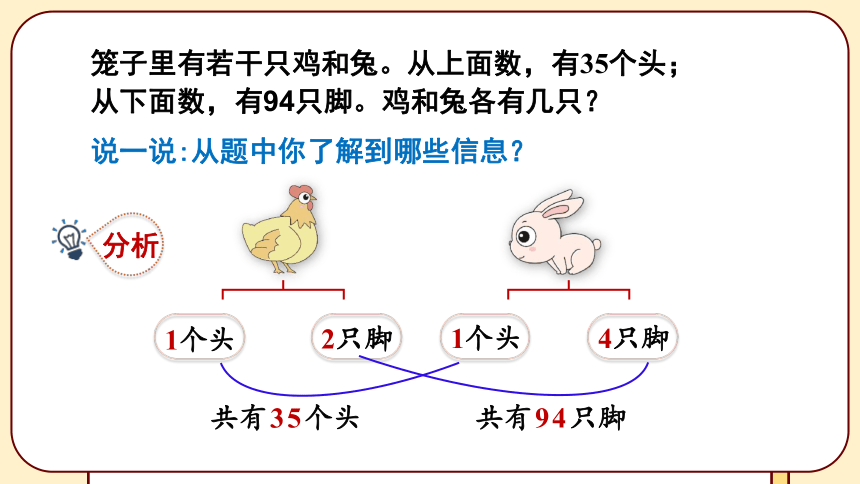
笼子里有若干只鸡和兔。从上面数,有35个头;
从下面数,有94只脚。鸡和兔各有几只?
分析
1个头
2只脚
1个头
4只脚
共有35个头
共有94只脚
你能解决这个问题吗?
化繁为简
笼子里有若干只鸡和兔。从上面数,有8个头;从下面数,有26只脚。
鸡和兔各有几只?
鸡和兔各有几只?
合作探究,学习新知
笼子里有若干只鸡和兔。从上面数,有8个头;从下面数,有26只脚。鸡和兔各有几只?
猜一猜
鸡和兔各有几只?
鸡 8 7 6 5
兔 0 1
脚 16 18
2
20
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
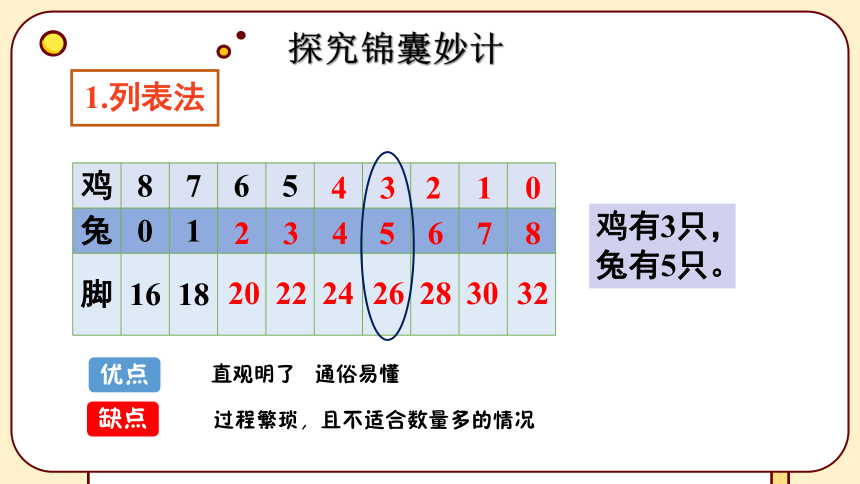
1.列表法
鸡有3只,兔有5只。
优点
缺点
直观明了 通俗易懂
过程繁琐,且不适合数量多的情况
探究锦囊妙计
2.画图法
“ ”表示鸡,“ ”表示兔
画法1→先全画鸡:
画法2→先全画兔:
鸡有3只,兔有5只。
3.假设法
2×8=16(只)
26-16=10(只)
4-2=2(只)
8-5=3(只)
10÷2=5(只)
3.假设法
4×8=32(只)
32-26=6(只)
4-2=2(只)
8-3=5(只)
6÷2=3(只)
检验:
3×2+5×4
=6+20
=26(只)
设鸡先得兔,设兔先得鸡;
一共有五步,最后要检验。
知识运用,巩固提高
笼子里有若干只鸡和兔,从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
2×35=70(只)
94-70=24(只)
4-2=2(只)
鸡:35-12=23(只)
兔:24÷2=12(只)
假设全是鸡
答:鸡有23只,兔有12只。
4×35=140(只)
4-2=2(只)
兔:35-23=12(只)
鸡:46÷2=23(只)
假设全是兔
140-94=46(只)
检验:
23×2+12×4
=46+48
=94(只)
自行车和三轮车共10辆,总共有26个轮子。
自行车和三轮车各有多少辆
2×10=20(个)
26-20=6(个)
3-2=1(个)
自行车:10-6=4(辆)
三轮车:6÷1=6(辆)
假设全是自行车
答:自行车有4辆,三轮车有6辆。
3×10=30(个)
3-2=1(个)
三轮车:10-4=6(辆)
自行车:4÷1=4(辆)
假设全是三轮车
30-26=4(个)
检验:
4×2+6×3
=8+18
=26(个)
小明有面值是5角、1元的人民币共17张,总共
是14元。面值是5角、1元的人民币各有多少张?
5×17=85(角)
140-85=55(角)
10-5=5(角)
5角:17-11=6(张)
1元:55÷5=11(张)
假设全是5角的人民币
答:面值是5角的人民币有6张,1元的人民币有11张。
10×17=170(角)
170-140=30(角)
10-5=5(角)
1元:17-6=11(张)
5角:30÷5=6(张)
假设全是1元的人民币
检验:
5×6+10×11
=30+110
=140(角)
1元=10角,
14元=140角
课堂小结,情感升华
你觉得“鸡兔同笼”问题有什么魅力之处?
拓展延伸,拓宽思路
请同学们在课后自学教科书P100的“阅读资料”,并上网查找更多关于
“鸡兔同笼”问题的解法内容。
难点:用假设法解决鸡兔同笼问题
数学广角--
历史激趣,揭示课题
我国古代数学名著《孙子算经》中记载了一道
数学趣题——“鸡兔同笼”问题 。
笼子里有若干只鸡和兔。从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
说一说:从题中你了解到哪些信息?
笼子里有若干只鸡和兔。从上面数,有35个头;
从下面数,有94只脚。鸡和兔各有几只?
分析
1个头
2只脚
1个头
4只脚
共有35个头
共有94只脚
你能解决这个问题吗?
化繁为简
笼子里有若干只鸡和兔。从上面数,有8个头;从下面数,有26只脚。
鸡和兔各有几只?
鸡和兔各有几只?
合作探究,学习新知
笼子里有若干只鸡和兔。从上面数,有8个头;从下面数,有26只脚。鸡和兔各有几只?
猜一猜
鸡和兔各有几只?
鸡 8 7 6 5
兔 0 1
脚 16 18
2
20
3
22
4
4
24
3
5
26
2
6
28
1
7
30
0
8
32
1.列表法
鸡有3只,兔有5只。
优点
缺点
直观明了 通俗易懂
过程繁琐,且不适合数量多的情况
探究锦囊妙计
2.画图法
“ ”表示鸡,“ ”表示兔
画法1→先全画鸡:
画法2→先全画兔:
鸡有3只,兔有5只。
3.假设法
2×8=16(只)
26-16=10(只)
4-2=2(只)
8-5=3(只)
10÷2=5(只)
3.假设法
4×8=32(只)
32-26=6(只)
4-2=2(只)
8-3=5(只)
6÷2=3(只)
检验:
3×2+5×4
=6+20
=26(只)
设鸡先得兔,设兔先得鸡;
一共有五步,最后要检验。
知识运用,巩固提高
笼子里有若干只鸡和兔,从上面数,有35个头;从下面数,有94只脚。鸡和兔各有几只?
2×35=70(只)
94-70=24(只)
4-2=2(只)
鸡:35-12=23(只)
兔:24÷2=12(只)
假设全是鸡
答:鸡有23只,兔有12只。
4×35=140(只)
4-2=2(只)
兔:35-23=12(只)
鸡:46÷2=23(只)
假设全是兔
140-94=46(只)
检验:
23×2+12×4
=46+48
=94(只)
自行车和三轮车共10辆,总共有26个轮子。
自行车和三轮车各有多少辆
2×10=20(个)
26-20=6(个)
3-2=1(个)
自行车:10-6=4(辆)
三轮车:6÷1=6(辆)
假设全是自行车
答:自行车有4辆,三轮车有6辆。
3×10=30(个)
3-2=1(个)
三轮车:10-4=6(辆)
自行车:4÷1=4(辆)
假设全是三轮车
30-26=4(个)
检验:
4×2+6×3
=8+18
=26(个)
小明有面值是5角、1元的人民币共17张,总共
是14元。面值是5角、1元的人民币各有多少张?
5×17=85(角)
140-85=55(角)
10-5=5(角)
5角:17-11=6(张)
1元:55÷5=11(张)
假设全是5角的人民币
答:面值是5角的人民币有6张,1元的人民币有11张。
10×17=170(角)
170-140=30(角)
10-5=5(角)
1元:17-6=11(张)
5角:30÷5=6(张)
假设全是1元的人民币
检验:
5×6+10×11
=30+110
=140(角)
1元=10角,
14元=140角
课堂小结,情感升华
你觉得“鸡兔同笼”问题有什么魅力之处?
拓展延伸,拓宽思路
请同学们在课后自学教科书P100的“阅读资料”,并上网查找更多关于
“鸡兔同笼”问题的解法内容。
