28.1 锐角三角函数—余弦、正切课件
文档属性
| 名称 | 28.1 锐角三角函数—余弦、正切课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 224.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-19 00:00:00 | ||
图片预览






文档简介
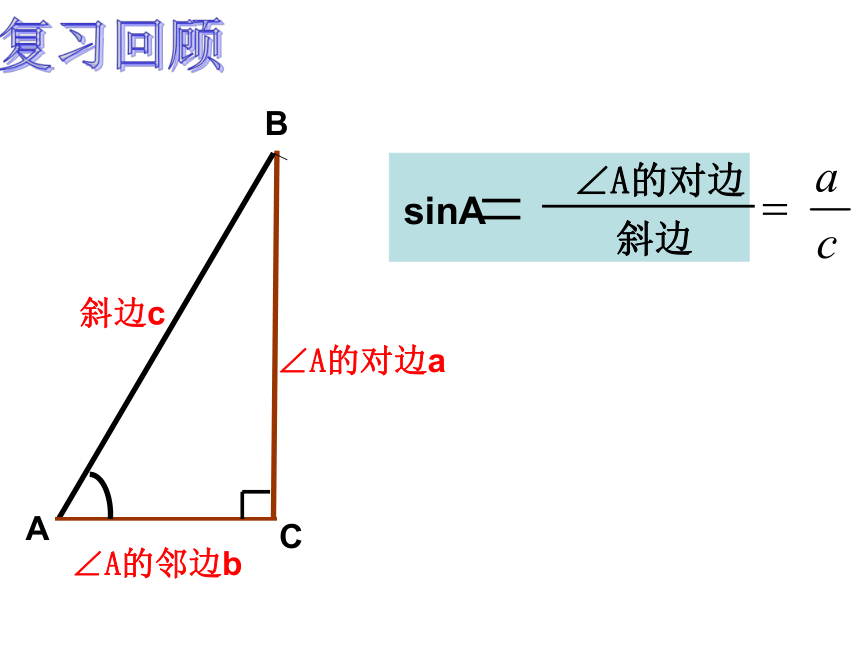
课件23张PPT。复习回顾1.在Rt△ABC中,∠C=90°,a=1,c=4,则sinA的( ).
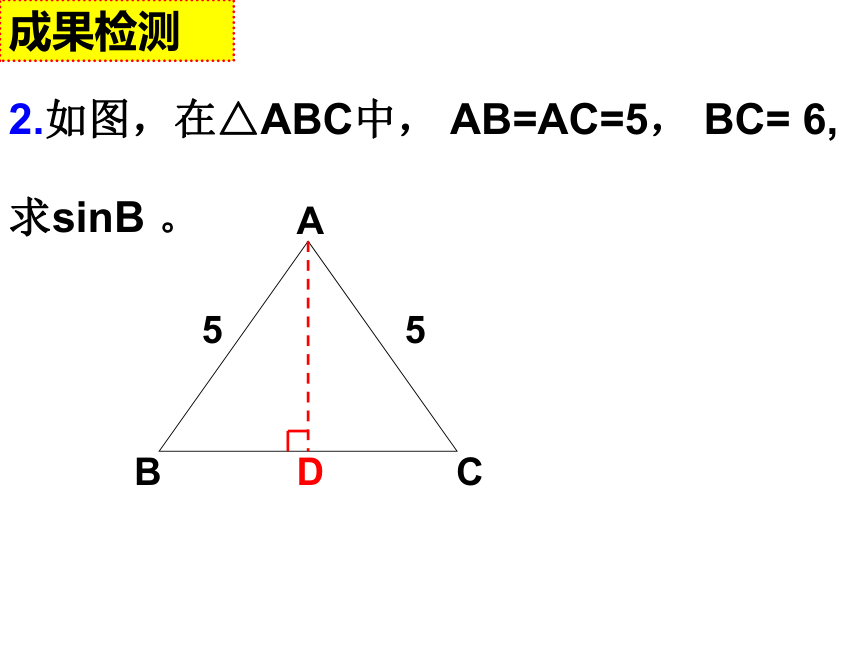
A.B成果检测 142.如图,在△ABC中, AB=AC=5, BC= 6,
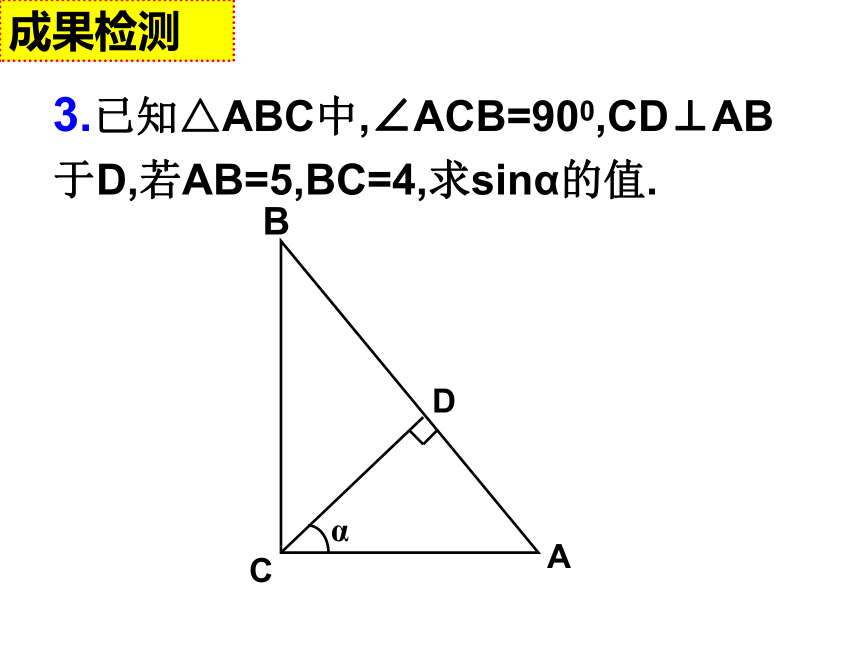
求sinB 。D成果检测 3.已知△ABC中,∠ACB=900,CD⊥AB于D,若AB=5,BC=4,求sinα的值.成果检测 小结提升 角的正弦值的计算:(1)直接在直角三角形中利用定义计算。(2)通过构造直角三角形进行计算。(3)转化为求与之相等的角的正弦值。4.如图:已知AB是⊙O的直径,CD是弦,
且CD⊥AB,AC=8,BC=6,求sin∠ABD更上一层楼成果检测 O5.如图2:P是平面直角坐标系上的一点,且点P的坐标为(3,4),则sin = P( 3 , 4 )
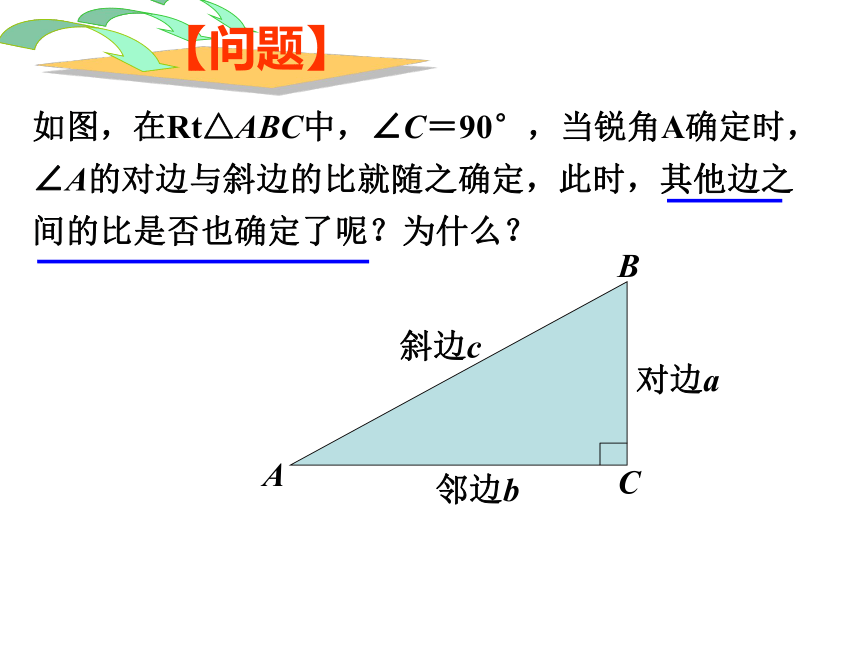
A成果检测 28.1 锐角三角函数(2)——余弦、正切【问题】如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么?一般地,在Rt△ABC中,∠C=90°,
把∠A的对边与邻边的比叫做∠A的正切
(tangent),记作tanA,即 锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.一般地,在Rt△ABC中,∠C=90°,
我们把∠A的邻边与斜边的比叫做∠A的余弦
(cosine),记作cosA,即∠B的正切如何表示呢?【试一试】2、在Rt△ABC中,∠C=90°,∠A=30°,求sinA , cosA , tanA的值。若∠A=45°,求sinA,cosA,tanA的值。1、在Rt△ABC中,∠C=90°,AB=13,AC=12,求sinA , cosA , tanA的值。13512x2xx 例1 如图,在Rt△ABC中,∠C=90°,BC=6,sinA= ,
求cosA、tanB的值. 例 题 示 范 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高。
求:?sinA= = = ;
?cosA= = = ;
?tan∠ACD= = = .练一练例2 已知锐角α的始边在x轴的正半轴上,顶点在原点,终边上有一点P的坐标为(2,3),求∠α的三个三角函数值. 例 题 示 范┓A 1. 如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC= ,求BC的长 3x5x4x5x【更上一层楼】 2. 如图,在矩形ABCD中,AB=10,BC=8,E为AD上的一点,沿CE将△CDE对折,点D正好落在AB边的F上。求tan∠AFE的值。【更上一层楼】 如图,把矩形纸片OABC放入直角坐标系中,使OA、OC分别落在x轴、y轴的正半轴上。连接AC,将△ABC沿AC翻折,点B落在该坐标平面内,设这个落点为D,CD交x轴于点E。若 ,AE=10,求点D的坐标。 变式3.直线m与y轴交点的纵坐标为-3,与x轴相交所成的锐角为α,若tanα=3/4,求直线m的解析式。【更上一层楼】4.如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若 , 那么 ( )B变式: 如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若AB=10,CD=6,求 .【更上一层楼】1、锐角三角函数的定义2、根据锐角三角函数值,设三角形边的长度3、合理构造直角三角形4、直角三角形两个锐角的三角函数之间的关系:今天作业:1 作业本(2) P20---21 2 全品P45---46 如图,在Rt△ABC中,∠C=90°1.求证:sinA=cosB,sinB=cosA2.求证:3.求证:延伸 如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是 .课外拓展
A.B成果检测 142.如图,在△ABC中, AB=AC=5, BC= 6,
求sinB 。D成果检测 3.已知△ABC中,∠ACB=900,CD⊥AB于D,若AB=5,BC=4,求sinα的值.成果检测 小结提升 角的正弦值的计算:(1)直接在直角三角形中利用定义计算。(2)通过构造直角三角形进行计算。(3)转化为求与之相等的角的正弦值。4.如图:已知AB是⊙O的直径,CD是弦,
且CD⊥AB,AC=8,BC=6,求sin∠ABD更上一层楼成果检测 O5.如图2:P是平面直角坐标系上的一点,且点P的坐标为(3,4),则sin = P( 3 , 4 )
A成果检测 28.1 锐角三角函数(2)——余弦、正切【问题】如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么?一般地,在Rt△ABC中,∠C=90°,
把∠A的对边与邻边的比叫做∠A的正切
(tangent),记作tanA,即 锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.一般地,在Rt△ABC中,∠C=90°,
我们把∠A的邻边与斜边的比叫做∠A的余弦
(cosine),记作cosA,即∠B的正切如何表示呢?【试一试】2、在Rt△ABC中,∠C=90°,∠A=30°,求sinA , cosA , tanA的值。若∠A=45°,求sinA,cosA,tanA的值。1、在Rt△ABC中,∠C=90°,AB=13,AC=12,求sinA , cosA , tanA的值。13512x2xx 例1 如图,在Rt△ABC中,∠C=90°,BC=6,sinA= ,
求cosA、tanB的值. 例 题 示 范 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高。
求:?sinA= = = ;
?cosA= = = ;
?tan∠ACD= = = .练一练例2 已知锐角α的始边在x轴的正半轴上,顶点在原点,终边上有一点P的坐标为(2,3),求∠α的三个三角函数值. 例 题 示 范┓A 1. 如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC= ,求BC的长 3x5x4x5x【更上一层楼】 2. 如图,在矩形ABCD中,AB=10,BC=8,E为AD上的一点,沿CE将△CDE对折,点D正好落在AB边的F上。求tan∠AFE的值。【更上一层楼】 如图,把矩形纸片OABC放入直角坐标系中,使OA、OC分别落在x轴、y轴的正半轴上。连接AC,将△ABC沿AC翻折,点B落在该坐标平面内,设这个落点为D,CD交x轴于点E。若 ,AE=10,求点D的坐标。 变式3.直线m与y轴交点的纵坐标为-3,与x轴相交所成的锐角为α,若tanα=3/4,求直线m的解析式。【更上一层楼】4.如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若 , 那么 ( )B变式: 如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若AB=10,CD=6,求 .【更上一层楼】1、锐角三角函数的定义2、根据锐角三角函数值,设三角形边的长度3、合理构造直角三角形4、直角三角形两个锐角的三角函数之间的关系:今天作业:1 作业本(2) P20---21 2 全品P45---46 如图,在Rt△ABC中,∠C=90°1.求证:sinA=cosB,sinB=cosA2.求证:3.求证:延伸 如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是 .课外拓展
