【高考解密】2025年高考数学--高考试题中统计5分小题问题的类型与解法
文档属性
| 名称 | 【高考解密】2025年高考数学--高考试题中统计5分小题问题的类型与解法 |  | |
| 格式 | doc | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-03 18:29:07 | ||
图片预览




文档简介
高考试题中统计5分小题问题的类型与解法
统计问题是近几年高考的热点内容之一。可以这样毫不夸张地说,只要是高考试卷,就必然涉及统计问题。从题型上看,可能是选择题(或填空题),也可能是大题,这里主要探导统计的5分小题问题;难度系数为低(或中)档。纵观近几年高考(或高三诊断考试)试卷,归结起来统计问题主要包括:①统计抽样的基本方法及运用;②统计表和统计图及运用;③统计指标计算及运用;④两个随机变量之间的相关关系及运用;⑤线性回归方程和独立性检验等几种类型。各种类型问题结构上具有一定的特征,解答方法也有一定的规律可寻。那么在实际解答统计5分小题问题时,到底应该如何抓住问题的结构特征,快捷,准确的解答问题呢?下面通过近几年高考(过高三诊断考试)试题的详细解析来回答这个问题。
【典例1】解答下列问题:
1、普法知识宣传小组打算从某小区的2000人中抽取25人进行法律知识培训,拟采取系统抽样方式,为此将他们一一编号为1-2000,并对编号由小到大进行分段,假设从第一个号码段中随机抽取的号码是2,那么从第三个号码段中抽出的号码为( ) (成都市高2021级高三一诊)
A 52 B 82 C 162 D 252
2、某区域有大型城市18个,中型城市12个,小型城市6个,为了解该区域城市空气质量情况,现采用分层抽样的方法抽取6个城市进行调查,则应抽取的大型城市的个数为 (成都市2019级高三二诊)
3、为了加强全民爱眼意识,提高民簇健康素质,1996年,卫生部,教育部,团中央等12个部委联合发出通知,将爱眼日活动列为国家节日之一,并确定每年的6月6日为“全国爱眼日”,某校高二(1)班有40名学生,学号为01到40,线采用随机数表法从该班抽取5名学生参加“全国爱眼日”宣传活动,已知随机数表中第六行至第七行的各数如下:
4、若从随机数表第6行第9列的数开始向右读,则抽取的第5名学生的学号是( )(成都市2021高三零诊)
A 17 B 23 C 35 D 37
5、某中学有高中生1500人,初中生1000人,为了解该校学生自主锻炼的时间,采用分层抽样的方法从高中学生和初中学生中抽取一个容量为n的样本,若样本中高中学生恰有30人则n的值为( )(成都市2020高三二诊)
A 20 B 50 C 40 D 60
6、下列抽样方法是简单随机抽样方法的是( )
A在某年明信片的销售活动中,规定每100万张为一个开奖组,通过随机抽取的方式确定号码的后四位为2700的为三等奖;B某车间包装一种产品,在自动包装的传送带上,每隔30分钟抽取一包产品,称其重量是否合格;C某学校分别从行政人员,教师,后勤人员抽取2人,14人,4人了解对学校机构改革的意见;D用抽签的方法从10件从产品中抽取3件进行质量检验。
『思考问题1』
(1)【典例1】是统计抽样基本方法及运用的问题,解答这类问题需要理解简单随机抽样,系统抽样和分层抽样的定义,了解简单随机抽样,系统抽样和分层抽样的特征与适用范围,掌握简单随机抽样,系统抽样和分层抽样的基本方法;
(2)运用抽签法必须注意两个基本条件:①抽签是否方便,②号签是否容易搅匀,一般地当总体容量和样本容量较小时可以采用抽签法;
(3)运用随机数表时,若遇到三位数或四位数,可以选择随机数表中某行某列的数字计起,每三个(或四个)作为一个单位,自左向右选取,有超过总体号码或重复号码舍去;
(4)系统抽样的特征是:①总体容量较大,②样本容量较大,③总体中各个个体之间没有明显的差异,④每个个体被抽到的可能性相等;
(5)系统抽样的基本方法是:①将总体中的个体进行统一编号,②把总体平均分成若干个部分(若总体容量不能被样本容量整除时,可以将总体随机剔除几个个体来确定分段间隔),③在第一个部分用简单随机抽样的方法确定开始的个体编号x,④按照每一组的个体数确定个体之间相隔的距离抽取样本;
(6)分层抽样的特征是:①总体容量较大,②总体由几个个体差异明显的部分构成;
(7)各层样本单位数的确定可按公式:某层抽取的样本数=样本数,通过计算来确定。
[练习1]解答下列问题:
1、某单位有840名职工,现采用系统抽样方法抽取42人做问卷调查,将840人按1,2,------,840随机编号,则抽取的42人中,编号落在区间[481,720]的人数为( )
A 11 B 12 C 13 D 14
2、将参加夏令营的600名学生编号为001,002,-------,600,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的号码为003,这600名学生分住在三个营区,从001到300在第I营区,从301到495在第II营区,从496到600在第III营区,三个营区被抽中的人数依次为( )
A 26,16,8 B 25,17,8 C 25,16,9 D 24,17,9
【典例2】解答下列问题:
1、“数九”从每年“冬至”当天开始计算,每九天为一个单位,冬至后的第81天,“数九”结束,天气九变得温暖起来。如图,以温江国家基准气象站为代表记录了20232024从“一九”到“九九”成都市的“平均气温”和“多年平均气温”(单位:),下列说法正确的是( )(成都市高2021级高三三诊)
A “四九”以后成都市“平均气温” 一直上升
B “四九”成都市“平均气温”较“多年平均气温”低0.1
C “一九” 到“五九” 成都市“平均气温” 的方差小于“多年平均气温”的方差
D “一九” 到“九九” 成都市“平均气温” 的极差小于“多年平均气温”的极差
1、全国文明典范城市是以全国文明城市为基础的文明城市典范,是城市治理“桂冠上的明珠”,为争创全国文明典范城市,某城市特邀请甲,乙两组评委分表从公共服务,文化建设,社会治理等10个不同维度对城市建设进行评分,每个维度满分为10分,现将两组评委的评分制成如图所示的茎叶图,其中茎叶图中茎部分是得分的个位数,叶部分是得分的小数,则下列结论中正确的是( )(成都市高2021级高三零诊)
A 甲组评分的平均数小于乙组评分的平均数 B 甲,乙两组评分的中位数不相同
C 甲组评分的极差大于乙组评分的极差 D 甲组评分的众数小于乙组评分的众数
2、从某小区随机抽取100户居民用户进行月用电量调查,发现他们的月用电量 50—300kw.h之间,适当分组(每组为左闭右开区间)后绘制成如图所示的频率分布直方图,则直方图中x的值以及在被调查的用户约用电量落在区间[100,250)内的户数分布为( )(成都市2020级高三零诊)
A 0.0046 ,72 B 0.0046,70 C 0.0042 ,72 D 0.0042 ,70
甲 乙
3、分别统计了甲,乙两位同学16周的各周 6 1 5
课外体育运动时长(单位:h),得到如表所 8 5 3 0 6 3
示的茎叶图: 7 5 3 2 7 4 6
则下列结论中错误的是( )(2022全国高考 6 4 2 1 8 1 2 2 5 6 6 6 6
乙卷文) 4 2 9 0 2 3 8
A 甲同学周课外体育运动时长的样本中位数为7.4 10 1 B 乙同学周课外体育运动时长的样本平均数大于8 C 甲同学周课外体育运动时长大于8的概率的估计值大于0.4 D 乙同学周课外体育运动时长大于8的概率的估计值大于0.6
4、为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )(2021全国高考甲卷)
A该地农户家庭年收入低于4.5万元的农户比率估计为6%
B该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C估计该地农户家庭年收入的平均值不超过6.5万元
D根据该地有一半以上农户,其家庭年收入介于4.5万元至8.5万元之间
5、如图,是某赛季甲,乙两名篮球运动员9场比赛 甲 乙
所得分数的茎叶图,则下列说法错误的是( )(20 0 8
20成都市高三零诊)A 甲所得分数的极差为22 B 7 5 1 1 1 2 6 8
乙所得分数的中位数为18 C 两人所得分数的众数相 4 2 2 0 2 0 2 2
等D 甲所得分数的平均数低于乙所得分数的平均数 3 2 3 1
6、某校随机抽取100名同学进行“垃圾分类”的问卷测试,测试结果发现这100名同学的得分都在[50,
100]内,按得分分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图,则这100名同学得分的中位数为( )(2020成都市高三一诊)
A 72.5 B 75 C 77.5 D 80
『思考问题2』
(1)【典例2】是统计表和统计图及运用的问题,解答这类问题需要理解统计表,茎叶图和频率分布直方图的定义,掌握制作统计表,茎叶图和频率分布直方图的基本作法,注意统计表,茎叶图和频率分布直方图的运用;
(2)茎叶图的特征是:①茎叶图能够看到真实的数据,没有任何信息损失;②茎叶图便于记录和表示;③茎叶图只便于表示两位有效数字的数据;④茎叶图也只方便记录两组数据;
(3)茎叶图的基本画法是:①用两短竖线把图分成两个部分;②两组数据中选一组放左边,另一组放右边;③把数据的十位数记在两短竖线之间;④将数据的个位数分别记在左右两边;
(4)解答与频率分布直方图相关问题的关键是读懂频率分布直方图,频率分布直方图中的每一个小矩形的面积是指样本数据落在该区域的频率,所有小矩形面积的和为1;
(5)作频率分布直方图的基本方法是:①求出原始数据的极差(最大值与最小值的差);②确定组数与组距;③确定各组的起始点与终点;④列出统计数据分布表;⑤画出频率分布直方图;
【典例3】解答下列问题:
1、某农业研究部门在面积相等的100块稻田种植一种新型水稻,得到各块稻田的亩产量(单位:千克)并整理如下表:
亩产量[900,950)[950,1000)[1000,1050)[1050,1100 )[1100,1150)[1150,
频数 6 12 18 30 24 10
根据表中数据,下列结论正确的是( )(2024全国高考新高考II)
A 100块稻田亩产量的中位数是1050千克
B 100块稻田亩产量低于1100千克的稻田所占比例超过80%
C 100块稻田亩产量的极差介于200千克到300千克之间
D 100块稻田亩产量的平均值介于900千克到1000千克之间
2、有一组样本数据:,,------,,其中是最小值,是最大值,其平均数为,方差为,极差为m,中位数为t,去除其中的最小值和最大值后,余下数据的平均数为,方差为,极差为,中位数为,则下列结论不一定正确的是( )(2023全国高考新高考I)
A ,,, 的平均数等于,,------,的平均数 B ,,, 的中位数等于,,------,的中位数 C ,,, 的标准差不小于,,------,的标准差 D ,,, 的极差不大于,,------,的极差
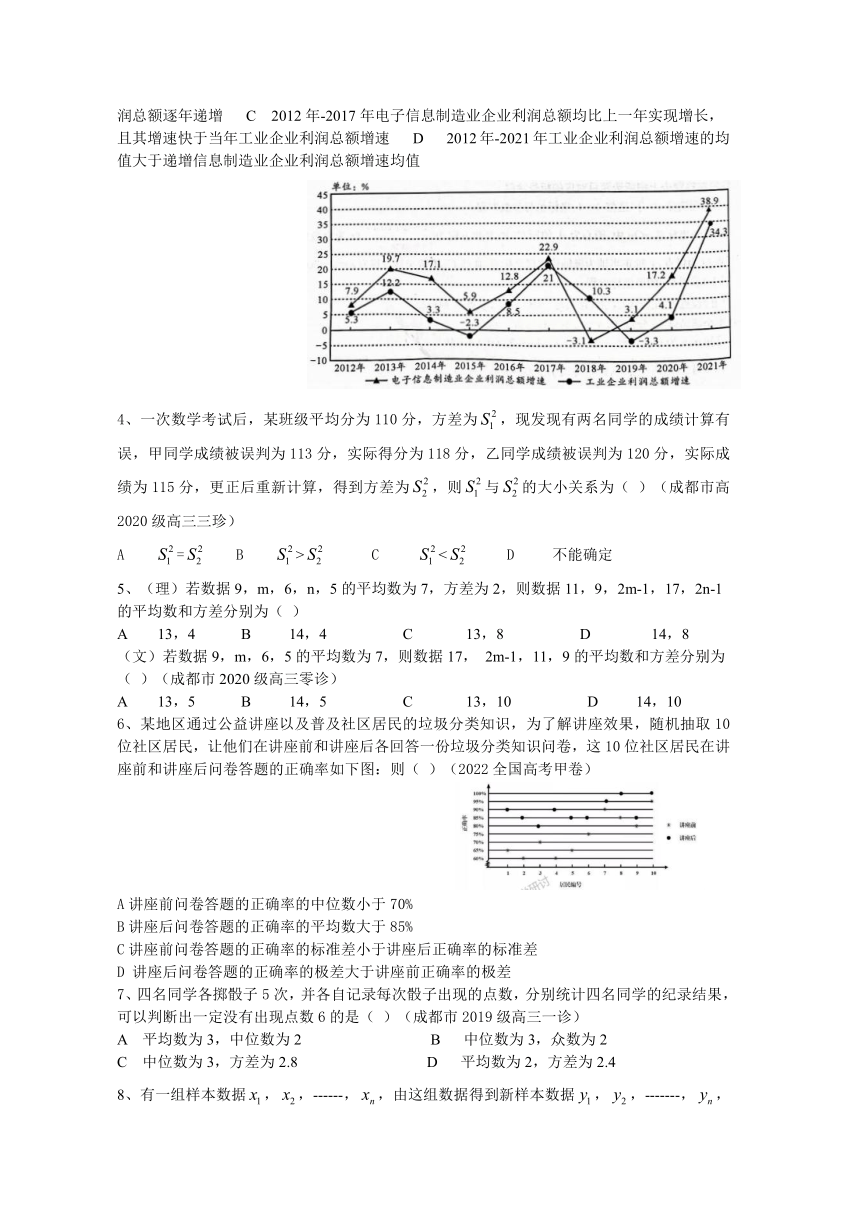
3、下图为2012年-2021年我国电子信息制造业企业和工业企业利润总额增速情况折线图,根据该图,下列结论正确的是( ) (成都市高2020级高三一诊)
A 2012年-2021年电子信息制造业企业利润总额逐年递增 B 2012年-2021年工业企业利
润总额逐年递增 C 2012年-2017年电子信息制造业企业利润总额均比上一年实现增长,且其增速快于当年工业企业利润总额增速 D 2012年-2021年工业企业利润总额增速的均值大于递增信息制造业企业利润总额增速均值
4、一次数学考试后,某班级平均分为110分,方差为,现发现有两名同学的成绩计算有误,甲同学成绩被误判为113分,实际得分为118分,乙同学成绩被误判为120分,实际成绩为115分,更正后重新计算,得到方差为,则与的大小关系为( )(成都市高2020级高三三珍)
A = B > C < D 不能确定
5、(理)若数据9,m,6,n,5的平均数为7,方差为2,则数据11,9,2m-1,17,2n-1的平均数和方差分别为( )
A 13,4 B 14,4 C 13,8 D 14,8
(文)若数据9,m,6,5的平均数为7,则数据17, 2m-1,11,9的平均数和方差分别为( )(成都市2020级高三零诊)
A 13,5 B 14,5 C 13,10 D 14,10
6、某地区通过公益讲座以及普及社区居民的垃圾分类知识,为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如下图:则( )(2022全国高考甲卷)
A讲座前问卷答题的正确率的中位数小于70%
B讲座后问卷答题的正确率的平均数大于85%
C讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D 讲座后问卷答题的正确率的极差大于讲座前正确率的极差
7、四名同学各掷骰子5次,并各自记录每次骰子出现的点数,分别统计四名同学的纪录结果,可以判断出一定没有出现点数6的是( )(成都市2019级高三一诊)
A 平均数为3,中位数为2 B 中位数为3,众数为2
C 中位数为3,方差为2.8 D 平均数为2,方差为2.4
8、有一组样本数据,,------,,由这组数据得到新样本数据,,-------,,其中=+c(i=1,2,-----,n),c为非零常数,则( )(2021全国高考新高考I)
A 两组样本数据的样本平均数相同 B 两组样本数据的样本中位数相同
C 两组样本数据的样本标准差相同 D 两组样本数据的样本极差相同
『思考问题3』
(1)【典例3】是统计指标及运用的问题,解答这类问题需要理解平均数,方差,标准差的定义,掌握求平均数,方差,标准差的基本求法;
(2)总体估计的常用方法有:①点估计;②区间估计;
(3)点估计是直接运用样本指标作为总体指标,常用的样本指标有:①样本的平均数;②样本的标准差;③样本的方差;常用的总体指标有:①总体的平均数;②总体的标准差;③总体的方差;
(4)区间估计是根据问题要求可靠程度去确定总体指标取值的区间,其基本方法是:①由问题要求的可靠程度确定抽样的平均误差;②根据抽样平均误差确定抽样误差的允许范围;③根据抽样误差的允许范围确定总体指标的取值范围。
[练习3]解答下列问题:
1、下列统计量中,能度量样本,,------,的离散程度的是( )
A 样本,,------,的标准差 B 样本,,------,的中位数
C 样本,,------,的极差 D 样本,,------,的平均数
2、甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是:,分别表示甲乙
甲 0 1 0 2 2 0 3 1 2 4
乙 2 2 1 1 1 2 1 1 0 1
两组数据的平均数,,分别表示甲乙两组数据的方差,则下列选项正确的是( )(成都市2021高三一诊)
A = ,> B >,> C <,< D >,<
3、某市环境保护局公布了该市A,B两个景区2014年至2020年各年的全年空气质量优良天数的数据,现根据这些数据绘制了如图所示的折线图,则由该折线图得出的下列结论中正确的是( )(成都市2021高三三诊)
A 景区A这7年的空气质量优良天数的极差为98 B 景区B这7年的空气质量优良天数的中位数为283 C 分别记景区A,B这7年的空气质量优良天数的众数为,,则>
D分别记景区A,B这7年的空气质量优良天数的标准差为 ,,则 >
4、(理)在一组样本数据中,1,2,3,4出现的频率分别为,,,,且=1,
则下列四种情形中,对应样本的标准差最大的一组是( )
A ==0.1,==0.4 B ==0.4,==0.1
C ==0.2,==0.3 D ==0.3,==0.2
(文)设一组样本数据,,-------,的方差为0.01,则数据10,10,-------,10的方差为( )(2020全国高考新课标III)
A 0.01 B 0.1 C 1 D 10
【典例4】解答下列问题:
1、 对变量x,y有观测数据(,)(i),得散点图1;对变量u,v有观测数据(,
)(i)得散点图2,表示变量x,y之间的线性相关系数,表示变量u,v之间的线性相关系数,则下列说法正确的是( )(成都市高2021级高三二诊)
A 变量x,y呈正相关,且||<|| B 变量x,y呈负相关,且||>||
C 变量x,y呈正相关,且||>|| D 变量x,y呈负相关,且||<||
2、 如图,由观察数据(,)(i=1,2,3,4,5,6)的散点图可知,y与x的关系可以
用模型y=blnx+a拟合,设z=lnx,利用最小二乘法求得y关于z的回归方程=z+1,已知=,=18,则=( )(成都市高2021级高三三诊)
A B C 1 D
3、下列命题中错误的是( )(成都市高2020级高三一诊)
A 在回归分析中,相关系数r的绝对值越大,两个变量的线性相关性越强 B 对分类变量X与Y,它们的随机变量的观测值k越小,说明“X与Y有关系”的把握性越大 C 线性回归直线=x+恒过点(,) D 在回归分析中,残差平方越小,模型的拟合效果越好
『思考问题4』
(1)【典例4】是判断两个随机变量相关关系和线性回归方程及运用的问题,解答这类问题需要理解两个随机变量相关和线性回归方程的定义,掌握判断两个随机变量是否具有相关关系和建立线性回归方程及回归分析的基本方法;
(2)判断两个随机变量是否相关的基本方法是:①根据数据作出随机变量的散点图,由散点图进行判断;②运用相关系数的计算公式,通过运算求出相关系数的值,根据相关系数值的大小进行判断;
(3)散点图法的基本方法是:①根据两个变量的一组对应值作出散点 图,②运用散点图判断两个随机变量是否具有相关关系;
(4)相关系数法的基本方法是:①根据两个变量的一组对应值运用公式计算相关系数的值,
②根据计算结果判断两个随机变量是否具有相关关系;
(5)判断两个变量是正相关还是负相关的常用方法是:①散点图法,②相关系数法,③运用线性回归方程=x+中的系数,若 > 0,为正相关;若 < 0为负相关。
(6)建立线性回归方程的基本方法是:①判断两个变量是否具有线性相关关系,②运用公式:
=, =- 求出回归系数,(也可以用待定系数法,即根据回归直线过样本点的中心求系数,),③写出回归直线方程;
(6)回归分析及回归预测的基本方法是:①依据回归直线方程视为变量y是变量x(或t)的一次函数,②将变量x(或t)的值代入回归直线方程求出变量y的值;③得出统计预测结果。
[练习4]解答下列问题:
1、某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:)的关系,在20个不同温度条件下进行种子发芽率实验,由实验数据(,)(i=1,2------,20)得到如下散点图:由此散点图,在10至40之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型是( )(2020全国高考新课标I)
A y=a+bx B y=a+b C y=a+b D y=a+blnx
2、某实验室对小白鼠体内x,y两项指标进行 小白鼠体内x 120 110 125 130 115
研究,连续五次实验所测得的这两项指标数据如 小白鼠体内y 92 83 90 96 89
表所示,已知y与x具有线性相关关系,利用表中数据求得回归直线方程为=x+,若下一次实验中x=170,利用该回归直线方程预测得=117,则的值为 (成都市2020
高三三诊)
【典例5】解答下列问题:
1、在某大学一食品超市,随机询问了70名不同性别 女 男 总计
的大学生在购买食物时是否查看营养说明,得到如下 要查看营养说明 15 25 40
的列联表:(成都市2019级高三三珍) 不查看营养说明 20 10 30
附:=其中n=a+b+c+d。 总计 35 35 70
P() 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005
0.455 0.708 1.323 2.702 2.706 3.841 5.024 6.635 7.879
根据列联表的独立性检验,则下列说法正确的是( )
A 在犯错误的概率不超过0.05的前提下,认为该校大学生在购买食物时要查看营养说明的人数中男生人数更多 B在犯错误的概率不超过0.010的前提下,认为该校大学生在购买食物时要查看营养说明的人数与不查看营养说明的人数比是 C 在犯错误的概率不超过0.025的前提下,认为性别与是否查看营养说明有关 D 在犯错误的概率不超过0.010的前提下,认为性别与是否查看营养说明有关
『思考问题5』
(1)【典例5】是独立性检验的问题,解答这类问题需要理解分类变量,独立性检验的定义,了解2x2列联表的意义,掌握独立性检验的基本方法;
(2)比较两个分类变量是否有关的基本方法是:①计算的值进行判断,越大两个分类变量有关的可能性越大;②计算|ad-bc|的值进行判断,|ad-bc|越大两个分类变量有关的可能性越大;
(3)独立性检验的基本方法是:①根据样本数据制成2x2列联表,②运用公式= 计算的观察值,③比较与临界值的大小,作出推断。
【典例6】解答下列问题:
1、为了解推动出口后某收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后某收入的样本均值=21,样本方差=0.01,已知该种植区以往的某收入服从正态分布N(1.8,),假设推动出口后的某收入Y服从正态分布N(,),则( )(2024全国高考新高考I)(若随机变量Z服从正态分布N(1u,),则p(Z<u+)0.8413)
A p(X>2)>0.2 B p(X>2)<0.5 C p(X>2)>0.5 D p(X>2)<0.8
2、随机变量X服从正态分布N(2,),若p(22.5)= (2022全国高考新高考II)
『思考问题6』
(1)【典例6】是与正太分布相关的问题,解答这类问题需要理解正太曲线,正太分布的定义,了解正太曲线的性质,掌握正太分布下概率计算的基本方法;
(2)正太曲线的主要性质是:①曲线在x轴的上方,且与x轴不相交;②正态曲线的图像关于直线x=u对称;③曲线在x=u时达到高峰值,由这一点向左,右两边延伸时,曲线逐渐降低;
(3)正太变量在(-∞,+∞)内取值的概率是1,对于固定的u,来说,随机变量在(u-,u+)上的取值的概率随着的减小而增大,即越小,随机变量X取值落在(u-,u+)的概率越大。
[练习6]解答下列问题:
1、某物理量的测量结果服从正太分布N(10,),下列结论中不正确的是( )(2021全国高考新高考II)
A 越小,该物理量在一次测量中在(9.9,10.1)的概率越大 B 越小,该物理量在一次测量中大于10的概率为0.5 C 越小,该物理量在一次测量中小于9.99与大于10.01的概率相等 D 越小,该物理量在一次测量中落在(9.9,10.2)与落在(10,10.3)的概率相等
高考试题中统计5分小题问题的类型与解法
统计问题是近几年高考的热点内容之一。可以这样毫不夸张地说,只要是高考试卷,就必然涉及统计问题。从题型上看,可能是选择题(或填空题),也可能是大题,这里主要探导统计的5分小题问题;难度系数为低(或中)档。纵观近几年高考(或高三诊断考试)试卷,归结起来统计问题主要包括:①统计抽样的基本方法及运用;②统计表和统计图及运用;③统计指标计算及运用;④两个随机变量之间的相关关系及运用;⑤线性回归方程和独立性检验等几种类型。各种类型问题结构上具有一定的特征,解答方法也有一定的规律可寻。那么在实际解答统计5分小题问题时,到底应该如何抓住问题的结构特征,快捷,准确的解答问题呢?下面通过近几年高考(过高三诊断考试)试题的详细解析来回答这个问题。
【典例1】解答下列问题:
1、 普法知识宣传小组打算从某小区的2000人中抽取25人进行法律知识培训,拟采取系统抽
样方式,为此将他们一一编号为1-2000,并对编号由小到大进行分段,假设从第一个号码段中随机抽取的号码是2,那么从第三个号码段中抽出的号码为( ) (成都市高2021级高三一诊)
A 52 B 82 C 162 D 252
【解析】
【考点】①系统抽样法定义与性质;②系统抽样法的基本方法。
【解题思路】根据系统抽样法的性质,运用系统抽样法的基本方法,结合问题条件求出从第三个号码段中抽出的号码就可得出选项。
【详细解答】=80,第一个号码段中随机抽取的号码是2, 从第三个号码段中抽出的号码为162,C正确,选C。
2、某区域有大型城市18个,中型城市12个,小型城市6个,为了解该区域城市空气质量情况,现采用分层抽样的方法抽取6个城市进行调查,则应抽取的大型城市的个数为 (成都市2019级高三二诊)
【解析】
【考点】①分层抽样方法定义与性质;②求分层抽样方法中每层抽取数的基本方法。
【解题思路】根据分层抽样的性质,运用求分层抽样方法中每层抽取数的基本方法就可求出应抽取的大型城市的个数。
【详细解答】该区域有大型城市18个,中型城市12个,小型城市6个,用分层抽样的方法抽取6个城市, 应抽取的大型城市的个数为6=6=3(个 )。
3、为了加强全民爱眼意识,提高民簇健康素质,1996年,卫生部,教育部,团中央等12个部委联合发出通知,将爱眼日活动列为国家节日之一,并确定每年的6月6日为“全国爱眼日”,某校高二(1)班有40名学生,学号为01到40,现采用随机数表法从该班抽取5名学生参加“全国爱眼日”宣传活动,已知随机数表中第六行至第七行的各数如下:若从第六行
的第十列开始,由左向右依次选取两个数字,则抽取到的第五名学生的编号为( )
A 20 B 17 C 37 D 23
【解析】
【考点】①随机数表定义与性质;②运用随机数表抽样的基本方法。
【解题思路】根据分层抽样的性质,运用求分层抽样方法中每层抽取数的基本方法就可求出应抽取的大型城市的个数。
【详细解答】采用随机数表法,且从第六行的第十列开始,抽取的5名学生的编号分别为17,37,23,35,20,抽取到的第五名学生的编号为20,A正确,选A。
4、若从随机数表第6行第9列的数开始向右读,则抽取的第5名学生的学号是( )(成都市2021高三零诊)
A 17 B 23 C 35 D 37
【解析】
【考点】①随机数表法抽样的定义与性质;②随机数表法抽样的基本方法。
【解题思路】根据随机数表法抽样的性质和随机数表法抽样的基本方法,结合问题条件确定出第5名学生的学号就可得出选项。
【详细解答】抽样是从随机数表第6行第9列的数开始向右读, 第1名学生的学号为39,第2名学生的学号为17,第3名学生的学号为37,第4名学生的学号为23,第5名学生的学号为35,C错误,选C。
5、某中学有高中生1500人,初中生1000人,为了解该校学生自主锻炼的时间,采用分层抽样的方法从高中学生和初中学生中抽取一个容量为n的样本,若样本中高中学生恰有30人,则n的值为( )(成都市2020高三二诊)
A 20 B 50 C 40 D 60
【解析】
【考点】①样本容量定义与性质;②分层抽样定义与性质;③分层抽样各层抽样数的计算公式及运用;④计算分层抽样各层抽样数的基本方法。
【解题思路】根据分层抽样的性质,运用分层抽样各层抽样数的计算公式,结合问题条件得到关于n的方程,求解方程求出样本容量n的值就可得出选项。
【详细解答】n=30, n=30=50, B正确,选B。
6、下列抽样方法是简单随机抽样方法的是( )
A在某年明信片的销售活动中,规定每100万张为一个开奖组,通过随机抽取的方式确定号码的后四位为2700的为三等奖;B某车间包装一种产品,在自动包装的传送带上,每隔30分钟抽取一包产品,称其重量是否合格;C某学校分别从行政人员,教师,后勤人员抽取2人,14人,4人了解对学校机构改革的意见;D用抽签的方法从10件从产品中抽取3件进行质量检验。
【解析】
【知识点】①简单随机抽样的定义与性质;②简单随机抽样的基本方法。
【解题思路】运用简单随机抽样的性质和简单随机抽样的基本方法,对各选项进行判断就可得出选项。
【详细解答】对A,在100万张明信片中,后四位为2700的明信片每一万张中就有一张,属于系统抽样,A不正确;对B,在自动包装的传送带上,每隔30分钟抽取一包产品,属于等距抽样, B不正确;对C,分别从行政人员,教师,后勤人员抽取2人,14人,4人属于分层抽样, C不正确;对D,用抽签的方法从10件从产品中抽取3件符合简单随机抽样的特征, D正确,即选D。
『思考问题1』
(1)【典例1】是统计抽样基本方法及运用的问题,解答这类问题需要理解简单随机抽样,系统抽样和分层抽样的定义,了解简单随机抽样,系统抽样和分层抽样的特征与适用范围,掌握简单随机抽样,系统抽样和分层抽样的基本方法;
(2)运用抽签法必须注意两个基本条件:①抽签是否方便,②号签是否容易搅匀,一般地当总体容量和样本容量较小时可以采用抽签法;
(3)运用随机数表时,若遇到三位数或四位数,可以选择随机数表中某行某列的数字计起,每三个(或四个)作为一个单位,自左向右选取,有超过总体号码或重复号码舍去;
(4)系统抽样的特征是:①总体容量较大,②样本容量较大,③总体中各个个体之间没有明显的差异,④每个个体被抽到的可能性相等;
(5)系统抽样的基本方法是:①将总体中的个体进行统一编号,②把总体平均分成若干个部分(若总体容量不能被样本容量整除时,可以将总体随机剔除几个个体来确定分段间隔),③在第一个部分用简单随机抽样的方法确定开始的个体编号x,④按照每一组的个体数确定个体之间相隔的距离抽取样本;
(6)分层抽样的特征是:①总体容量较大,②总体由几个个体差异明显的部分构成;
(7)各层样本单位数的确定可按公式:某层抽取的样本数=样本数,通过计算来确定。
[练习1]解答下列问题:
1、某单位有840名职工,现采用系统抽样方法抽取42人做问卷调查,将840人按1,2,------,840随机编号,则抽取的42人中,编号落在区间[481,720]的人数为( )(答案:B)
A 11 B 12 C 13 D 14
2、将参加夏令营的600名学生编号为001,002,-------,600,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的号码为003,这600名学生分住在三个营区,从001到300在第I营区,从301到495在第II营区,从496到600在第III营区,三个营区被抽中的人数依次为( )(答案:B)
A 26,16,8 B 25,17,8 C 25,16,9 D 24,17,9
【典例2】解答下列问题:
1、“数九”从每年“冬至”当天开始计算,每九天为一个单位,冬至后的第81天,“数九”结束,天气九变得温暖起来。如图,以温江国家基准气象站为代表记录了20232024从“一九”到“九九”成都市的“平均气温”和“多年平均气温”(单位:),下列说法正确的是( )(成都市高2021级高三三诊)
A “四九”以后成都市“平均气温” 一直上升
B “四九”成都市“平均气温”较“多年平均气温”低0.1
C “一九” 到“五九” 成都市“平均气温” 的方差小于“多年平均气温”的方差
D “一九” 到“九九” 成都市“平均气温” 的极差小于“多年平均气温”的极差
【解析】
【考点】①平均数定义与性质;②方差定义与性质;③极差定义与性质;④统计直方图及运
用;⑤求一组数据平均数的基本方法;⑥求一组数据方差的基本方法;⑦求一组数据极差的基本方法。
【解题思路】根据平均数,方差和极差的性质,运用统计直方图和求一组数列平均数,方差与极差的基本方法,结合问题条件对各选项说法的正确与错误进行判断就可得出选项。
【详细解答】对A,从条件直方图可知,“八九”的“平均气温”比“七九”的“平均气温”低,A错误;对B,从条件直方图可知,“四九”的“平均气温”比“多年平均气温”高0.1,B错误;对C,从“一九” 到“五九” 成都市“平均气温”的平均数为==6.96(),成都市“多年平均气温”的平均数为==5.62(),成都市“平均气温”的方差为
==3.15536,成都市“多年平均气温”的方差数为==0.1350,>,C错误;对D,从“一九” 到“五九” 成都市“平均气温”的极差为10.6-5.4=5.2(), 成都市“多年平均气温”的极差为10.7-5.3=5.4(),5.2<5.4,D正确,综上所述D正确,选D。
2、全国文明典范城市是以全国文明城市为基础的文明城市典范,是城市治理“桂冠上的明珠”,为争创全国文明典范城市,某城市特邀请甲,乙两组评委分表从公共服务,文化建设,社会治理等10个不同维度对城市建设进行评分,每个维度满分为10分,现将两组评委的评分制成如图所示的茎叶图,其中茎叶图中茎部分是得分的个位数,叶部分是得分的小数,则下列结论中正确的是( )(成都市高2021级高三零诊)
A 甲组评分的平均数小于乙组评分的平均数 B 甲,乙两组评分的中位数不相同
C 甲组评分的极差大于乙组评分的极差 D 甲组评分的众数小于乙组评分的众数
【解析】
【考点】①茎叶图定义与性质;②数据平均数定义与性质;③数据中位数定义与性质;④数据极差定义与性质;⑤数据众数定义与性质。
【解答思路】根据茎叶图,数据平均数,中位数,极差和众数的性质,运用茎叶图的数据分别求出甲组,乙组评分的平均数,中位数,极差和众数,对各选项结论的正确与错误进行判断就可得出选项。
【详细解答】对A,==8.06,
==8.16,8.06<8.16, A正确;
对B, 甲组评委评分的中位数为=8.05,,乙组评委评分的中位数为
=8.05,8.05=8.05,B错误;对C, 甲组评委评分的极差为8.6-7.5=1.1,,乙组评委评分的极差为9.8-7.5=23,1.1<2.3,C错误;对D, 甲组评委评分的众数为8.3,,乙组评委评分的众数为7.8,8.3>7.8,D错误,综上所述A正确,选A。
3、从某小区随机抽取100户居民用户进行月用电量调查,发现他们的月用电量 50—300kw.h
之间,适当分组(每组为左闭右开区间)后绘制成如图所示的频率分布直方图,则直方图中x的值以及在被调查的用户约用电量落在区间[100,250)内的户数分布为( )(成都市2020级高三零诊)
A 0.0046 ,72 B 0.0046,70 C 0.0042 ,72 D 0.0042 ,70
【解析】
【考点】①频率分布直方图定义与性质;②频率定义与性质;③确定某一区间数据的基本方法。
【解答思路】根据频率分布直方图和频率的性质,求出x的值和区间[100,250)的频率,从而求出用电量落在区间[100,250)内的户数,就可得出选项。
【详细解答】由频率分布直方图可知,50(0.0024+0.0032+0.0038+x+0.0060)=50(0.0154
+x)=1, x=0.02-0.0154=0.0046, 用电量落在区间[100,250)内的频率为50(0.0038
0.0046+0.0060)=0.72,用电量落在区间[100,250)内的户数为1000.72=72(户),A正确,选A。 甲 乙
4、分别统计了甲,乙两位同学16周的各周 6 1 5
课外体育运动时长(单位:h),得到如表所 8 5 3 0 6 3
示的茎叶图: 7 5 3 2 7 4 6
则下列结论中错误的是( )(2022全国高考 6 4 2 1 8 1 2 2 5 6 6 6 6
乙卷文) 4 2 9 0 2 3 8
A 甲同学周课外体育运动时长的样本中位数为7.4 10 1 B 乙同学周课外体育运动时长的样本平均数大于8 C 甲同学周课外体育运动时长大于8的概率的估计值大于0.4 D 乙同学周课外体育运动时长大于8的概率的估计值大于0.6
【解析】
【考点】①茎叶图定义与性质;②中位数定义与求法;③平均数定义与求法;④统计估计的基本方法。
【解题思路】根据茎叶图的性质,运用求中位数和平均数的基本方法,结合问题条件分别求出甲同学周课外体育运动时长的样本中位数和乙同学周课外体育运动时长的样本平均数,利
用统计估计的基本方法,分别估计出甲同学周课外体育运动时长大于8的概率和乙同学周课外体育运动时长大于8的概率就可得出选项。
【详细解答】甲同学周课外体育运动时长的样本中位数为=7.4,乙同学周课外体育运动时长的样本平均数为
=8.50625>8,甲同学周课外体育运动时长大于8的概率的估计值为=0.375<0.4,乙同学周课外体育运动时长大于8的概率的估计值为=0.8125>0.8,C结论不正确,选C。
5、为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )(2021全国高考甲卷)
A该地农户家庭年收入低于4.5万元的农户比率估计为6%
B该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C估计该地农户家庭年收入的平均值不超过6.5万元
D根据该地有一半以上农户,其家庭年收入介于4.5万元至8.5万元之间
【解析】
【考点】①频率分布直方图的定义与性质;②频率的定义与基本求法;③统计估计的基本方法;④平均数计算公式及运用。
【解题思路】根据样频率分布直方图的性质和求频率的基本方法,结合问题条件分别求出该地农户家庭年收入低于4.5万元的农户,低于10.5万元的农户和介于4.5万元至8.5万元之间的农户的频率,运用计算平均数的公式求出该地农户家庭年收入的平均值,利用统计估计的基本方法就可得出选项。
【详细解答】该地农户家庭年收入低于4.5万元的农户比率为(0.02+0.04)1
=0.06,A正确;该地农户家庭年收入低于10.5万元的农户比率(0.02+0.04+
0.13+0.14+0.202)1=0.90,该地农户家庭年收入不低于10.5万元的农户比率为1-0.90=0.10,即B正确;该地农户家庭年收入的平均值为0.02(3+12+13+14)+0.04(4+11)+0.10(5+9+10)+0.146+0.20(7+8)=7.68>6.5,C错误,C结论不正确,选C。
6、如图,是某赛季甲,乙两名篮球运动员9场比赛 甲 乙
所得分数的茎叶图,则下列说法错误的是( )(20 0 8
20成都市高三零诊)A 甲所得分数的极差为22 B 7 5 1 1 1 2 6 8
乙所得分数的中位数为18 C 两人所得分数的众数相 4 2 2 0 2 0 2 2
等D 甲所得分数的平均数低于乙所得分数的平均数 3 2 3 1
【解析】
【考点】①茎叶图的定义与性质;②极差的定义与求法;③中位数的定义与求法;④众数的定义与求法;⑤平均数的定义与求法。
【解题思路】运用茎叶图的性质,结合问题条件分别求出甲所得分数的极差,乙所得分数的
中位数,甲,乙所得分数的众数和平均数就可得出选项。
【详细解答】甲所得分数的极差为33-11=22,A正确;乙所得分数的中位数为18,B正确;甲,乙所得分数的众数分别为22,22,C正确;甲,乙所得分数的平均数分别为= 21.8,
= 17.8,21.8>17.8,>,D错误,选D。
『思考问题2』
(1)【典例2】是统计表和统计图及运用的问题,解答这类问题需要理解统计表,茎叶图和频率分布直方图的定义,掌握制作统计表,茎叶图和频率分布直方图的基本作法,注意统计表,茎叶图和频率分布直方图的运用;
(2)茎叶图的特征是:①茎叶图能够看到真实的数据,没有任何信息损失;②茎叶图便于记录和表示;③茎叶图只便于表示两位有效数字的数据;④茎叶图也只方便记录两组数据;
(3)茎叶图的基本画法是:①用两短竖线分成把图分成两部分,②两组数据中选一组放左边,另一组放右边,③把数据的十位数记在两短竖线之间,④将数据的个位数分别记在左右两边;
(4)解答与频率分布直方图相关问题的关键是读懂频率分布直方图,频率分布直方图中的每一个小矩形的面积是指样本数据落在该区域的频率,所有小矩形面积的和为1;
(5)作频率分布直方图的基本方法是:①求出原始数据的极差(最大值与最小值的差);②确定组数与组距;③确定各组的起始点与终点;④列出统计数据分布表;⑤画出频率分布直方图;
[练习2]解答下列问题:
1、某校随机抽取100名同学进行“垃圾分类”的问卷测试,测试结果发现这100名同学的得分都在[50,100]内,按得分分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图,则这100名同学得分的中位数为()(2020成都市高三一诊)
A 72.5 B 75 C 77.5 D 80
(答案:A)
【典例3】解答下列问题:
1、某农业研究部门在面积相等的100块稻田种植一种新型水稻,得到各块稻田的亩产量(单位:千克)并整理如下表:
亩产量[900,950)[950,1000)[1000,1050)[1050,1100 )[1100,1150)[1150,
频数 6 12 18 30 24 10
根据表中数据,下列结论正确的是( )(2024全国高考新高考II)
A 100块稻田亩产量的中位数是1050千克
B 100块稻田亩产量低于1100千克的稻田所占比例超过80%
C 100块稻田亩产量的极差介于200千克到300千克之间
D 100块稻田亩产量的平均值介于900千克到1000千克之间
【解析】
【考点】①中位数定义与性质;②极差定义与性质;③平均数定义与性质;④求一组数据,中位数,极差和平均数的基本方法。
【解题思路】根据平均数,中位数和极差的性质,运用求一组数据,中位数,极差和平均数的基本方法,结合问题条件对各选项结论的正确与错误进行判断就可得出选项。
【详细解答】对A,6+12+18=36<50,100块稻田亩产量的中位数大于1050,A错误;对B, 100块稻田亩产量低于1100千克的稻田所占比例为 100%=66%
<80%,B错误;对C,100块稻田亩产量的极差大于1150-950=200,小于1200-900=300,100块稻田亩产量的极差介于200千克到300千克之间,C正确;对D,100块稻田亩产量的平均值为(9256+97512+102518+107530+112524+117510)=1067>1000,
D错误,综上所述,C正确,选C。
2、有一组样本数据:,,------,,其中是最小值,是最大值,其平均数为,
方差为,极差为m,中位数为t,去除其中的最小值和最大值后,余下数据的平均数为,方差为,极差为,中位数为,则下列结论不一定正确的是( )(2023全国高考新高考I)
A ,,, 的平均数等于,,------,的平均数 B ,,, 的中位数等于,,------,的中位数 C ,,, 的标准差不小于,,------,的标准差 D ,,, 的极差不大于,,------,的极差
【解析】
【考点】①一组数据平均数定义与性质;②一组数据中位数定义与性质;③一组数据标准差定义与性质;④一组数据极差定义与性质。
【解题思路】根据一组数据平均数,中位数,标准差和极差的性质,结合问题条件确定出数据的平均数,中位数,标准差和极差就可得出选项。
【详细解答】设:,,------,,分别为1,2,2,2,2,4,对A,,,,
的平均数为2,,,------,的平均数为,A错误;对B,,,, 的中位数为=2,,,------,的中位数为=2,B正确;对C,,,, 的标准差为0,,,------,的标准差为=,C错误;对D,,,, 的极差为2-2=0,,,------,的极差为4-1=3,0≤3,D正确,综上所述B,D正确,选BD。
3、下图为2012年-2021年我国电子信息制造业企业和工业企业利润总额增速情况折线图,根据该图,下列结论正确的是( ) (成都市高2020级高三一诊)
A 2012年-2021年电子信息制造业企业利润总额逐年递增 B 2012年-2021年工业企业利
润总额逐年递增 C 2012年-2017年电子信息制造业企业利润总额均比上一年实现增长,且其增速快于当年工业企业利润总额增速 D 2012年-2021年工业企业利润总额增速的均值大于递增信息制造业企业利润总额增速均值
【解析】
【考点】①统计折线图平定义与性质;②平均数定义与性质;③求平均数的基本方法。
【解题思路】根据统计折线图和平均数的性质,运用求平均数的基本方法,结合问题条件分别求出 2012年-2021年工业企业利润总额增速和电子信息制造业企业利润总额增速的均值
,对各选项的正确与错误进行判断就可得出选项。
【详细解答】从统计折线图可以看出,电子信息制造也企业和工业企业都有负的增速, 2012年-2021年电子信息制造业企业和工业企业利润总额都不是逐年递增,A,B错误;从统计折线图可以看出,2012年-2017年电子信息制造业企业利润总额均比上一年实现增长,且其增速快于当年工业企业利润总额增速, C正确; 2012年-2021年工业企业利润总额增速的均值为=9.34(%),2012年-2021年电子制造业企业利润总额增速的均值为
=14.24(%),9.34%<14.24%,
2012年-2021年工业企业利润总额增速的均值小于递增信息制造业企业利润总额增速均
值,D错误,C正确,选C。
4、一次数学考试后,某班级平均分为110分,方差为,现发现有两名同学的成绩计算有误,甲同学成绩被误判为113分,实际得分为118分,乙同学成绩被误判为120分,实际成绩为115分,更正后重新计算,得到方差为,则与的大小关系为( )(成都市高2020级高三三珍)
A = B > C < D 不能确定
【解析】
【考点】①平均数定义与性质;②方差定义与性质;③求一组数据平均数的基本方法;④求一组数据方差的基本方法。
【解题思路】根据平均数和方差的性质,运用求一组数列平均数和方差的基本方法,分别求出误判和实际数据的平均数和方差,从而得到与的大小关系就可得出选项。
【详细解答】误判时甲同学比实际少计了5分,乙同学比实际多计了5分,误判和实际的平均法不变,甲同学误判分与实际分和平均分的差的平方分别为9和64,,乙同学误判分与实际分和平均分的差的平方分别为100和25,9+100=109,64+25=89,109-89=20>0, > ,B正确,选B。
5、(理)若数据9,m,6,n,5的平均数为7,方差为2,则数据11,9,2m-1,17,2n-1的平均数和方差分别为( )
A 13,4 B 14,4 C 13,8 D 14,8
(文)若数据9,m,6,5的平均数为7,则数据17, 2m-1,11,9的平均数和方差分别为( )(成都市2020级高三零诊)
A 13,5 B 14,5 C 13,10 D 14,10
【解析】
【考点】①数据平均数定义与性质;②数据方差定义与性质;③求一组数据平均数的基本方法;④求一组数据方差的基本方法。
【解题思路】(理)根据数据平均数和方差的性质,运用求一组数据平均数和方程的基本方法,结合问题条件得到关于m,n的方程组,求解方程组求出m,n的值,从而求出数据11,9,2m-1,17,2n-1的平均数和方差,就可得出选项。(文)根据数据平均数和方差的性质,运用求一组数据平均数和方程的基本方法,结合问题条件得到关于m的方程,求解方程求出m的值,从而求出数据17, 2m-1,11,9的平均数和方差,就可得出选项。
【详细解答】(理)数据9,m,6,n,5的平均数为7,方差为2, m+n=35-(9+6+5)=15①,+ =10-(4+1+4)=1②,联立①②解得:m=8,n=7,11,9,2m-1,17,
2n-1为11,9,15,17,13,数据11,9,15,17,13的平均数为=13,
方差为=8,C正确,选C。
(文)数据9,m,6,5的平均数为7, m=28-(9+6+5)=8, 数据17,2m-1,11,9为数据17,15,11,9, 数据17,15,11,9的平均数为=13,方差为3、6、某地区通过公益讲座以及普及社区居民的垃圾分类知识,为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如下图:则( )(2022全国高考甲卷)
A讲座前问卷答题的正确率的中位数小于70%
B讲座后问卷答题的正确率的平均数大于85%
C讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D 讲座后问卷答题的正确率的极差大于讲座前正确率的极差
【解析】
【考点】①随机变量散点图定义与性质;②中位数定义与基本求法;③平均数定义与基本求法;④标准差定义与基本求法;⑤极差定义与基本求法。
【解题思路】根据随机变量散点图的性质,运用求中位数,平均数,标准差和极差的基本方法,结合问题条件分别求出讲座前问卷答题的正确率的中位数,讲座后问卷答题的正确率的平均数,讲座前问卷答题的正确率的标准差与讲座后正确率的标准差,讲座后问卷答题的正确率的极差与讲座前正确率的极差,就可得出选项。
【详细解答】讲座前问卷答题的正确率的中位数为=72.5%>70%,A错误;讲座后问卷答题的正确率的平均数为= =89.5
%>85%, B正确,选B。
7、四名同学各掷骰子5次,并各自记录每次骰子出现的点数,分别统计四名同学的纪录结果,可以判断出一定没有出现点数6的是( )(成都市2019级高三一诊)
A 平均数为3,中位数为2 B 中位数为3,众数为2
C 中位数为3,方差为2.8 D 平均数为2,方差为2.4
【解析】
【考点】①平均数定义与性质;②中位数定义与性质;③众数定义与性质;④方差定义与性质。
【解题思路】根据平均数,中位数,众数和方差的性质,运用求平均数,中位数,众数和方差的基本方法,对各选项进行判断就可得出选项。
【详细解答】设表示某名同学纪录自记每次骰子出现的点数由小到大排列时第i(i=1,2,3,4,5)次骰子出现的点数,对A,平均数为3,中位数为2, 这名同学的纪录结果中 ,骰子出现点数之和为35=15,=1或2,=1 或2,=2,++2+2+26, +15-69,当=3时,必有=6, A错误;对B,中位数为3,众数为2,==2,=3,++=2+2+3=7,,中有可能其中一个(或两个)是6,
B错误;对C,中位数为3,方差为2.8,=1或2或3,=1 或2或3,=3,当==1,=3时,,两个点数大于或等于3,平均数大于2,若平均数为3,+=35-5
=10,当=4时,=6, C错误;对D, 平均数为2,方差为2.4, =2.420=48,若,,,,有1次骰子出现的点数为6,不妨设=6,==16,方差3.2>2.4,,,,,中不可能有6D正确,选D。
8、有一组样本数据,,------,,由这组数据得到新样本数据,,-------,,其中=+c(i=1,2,-----,n),c为非零常数,则( )(2021全国高考新高考I)
A 两组样本数据的样本平均数相同 B 两组样本数据的样本中位数相同
C 两组样本数据的样本标准差相同 D 两组样本数据的样本极差相同
【解析】
【考点】①样本定义与性质;②样本平均数定义与性质;③样本中位数定义与性质;④样本
标准差定义与性质;⑤样本极差定义与性质;⑥求一组数据平均数,中位数,标准差和极差的基本方法。
【解题思路】根据样本,样本平均数,样本中位数,样本标准差和样本极差的性质,运用求一组数据平均数,中位数,标准差和极差的基本方法,结合问题条件分别求出两个样本数据的平均数,中位数,标准差和极差就可得出选项。
【详细解答】样本数据,,------,的平均数= ,新样本数据,,-------,的平均数= =+c,,A错误;样本数据,,------,的中位数与新样本数据,,-------,的中位数=+c,+c,B错误;样本数据,,------,的标准差=,新样本数据,,-------,的标准差==
==,C正确;样本数据,,------,的极差=-,新样本数据,,-------,的极=-=+c--c=-,D正确,C,D正确,选C,D。
『思考问题3』
(1)【典例3】是统计指标及运用的问题,解答这类问题需要理解平均数,方差,标准差的定义,掌握求平均数,方差,标准差的基本求法;
(2)总体估计的常用方法有:①点估计;②区间估计;
(3)点估计是直接运用样本指标作为总体指标,常用的样本指标有:①样本的平均数;②样本的标准差;③样本的方差;常用的总体指标有:①总体的平均数;②总体的标准差;③总体的方差;
(4)区间估计是根据问题要求可靠程度去确定总体指标取值的区间,其基本方法是:①由问题要求的可靠程度确定抽样的平均误差;②根据抽样平均误差确定抽样误差的允许范围;③根据抽样误差的允许范围确定总体指标的取值范围。
[练习3]解答下列问题:
1、下列统计量中,能度量样本,,------,的离散程度的是( )(2021全国高考新高考I)(答案:A,C)
A 样本,,------,的标准差 B 样本,,------,的中位数
C 样本,,------,的极差 D 样本,,------,的平均数
2、甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是:,分别表示甲乙两组数据的平均数,,分别表示甲乙两组数据的方差,则下列选项正确的
甲 0 1 0 2 2 0 3 1 2 4
乙 2 2 1 1 1 2 1 1 0 1
是( )(成都市2021高三一诊)(答案:B)
A = ,> B >,> C <,< D >,<
3、某市环境保护局公布了该市A,B两个景区2014年至2020年各年的全年空气质量优良天数的数据,现根据这些数据绘制了如图所示的折线图,则由该折线图得出的下列结论中正确的是( )(成都市2021高三三诊)(答案:D)
A 景区A这7年的空气质量优良天数的极差为98 B 景区B这7年的空气质量优良天数的中位数为283 C 分别记景区A,B这7年的空气质量优良天数的众数为,,则>
D分别记景区A,B这7年的空气质量优良天数的标准差为 ,,则 >
4、(理)在一组样本数据中,1,2,3,4出现的频率分别为,,,,且=1,
则下列四种情形中,对应样本的标准差最大的一组是( )(答案:B)
A ==0.1,==0.4 B ==0.4,==0.1
C ==0.2,==0.3 D ==0.3,==0.2
(文)设一组样本数据,,-------,的方差为0.01,则数据10,10,-------,10的方差为( )(2020全国高考新课标III)(答案:C)
A 0.01 B 0.1 C 1 D 10
【典例4】解答下列问题:
1、 对变量x,y有观测数据(,)(i),得散点图1;对变量u,v有观测数据(,
)(i)得散点图2,表示变量x,y之间的线性相关系数,表示变量u,v之间的线性相关系数,则下列说法正确的是( )(成都市高2021级高三二诊)
A 变量x,y呈正相关,且||<|| B 变量x,y呈负相关,且||>||
C 变量x,y呈正相关,且||>|| D 变量x,y呈负相关,且||<||
【解析】
【考点】①随机变量散点图定义与性质;②随机变量相关系数定义与性质;③随机变量正相关定义与性质;④随机变量负相关定义与性质。
【解题思路】根据随机变量散点图,相关系数,正相关和负相关的性质,结合问题条件对各选项说法的正确性进行判断就可得出选项。
【详细解答】根据随机变量x,y 的散点图可知,随机变量x,y呈正相关, B,D错误;根据随机变量散点图可知,随机变量x,y比随机变量u,v的线性相关更大, ||>||,
A错误,C正确,选C。
2、如图,由观察数据(,)(i=1,2,3,4,5,6)的散点图可知,y与x的关系可以
用模型y=blnx+a拟合,设z=lnx,利用最小二乘法求得y关于z的回归方程=z+1,已知=,=18,则=( )(成都市高2021级高三三诊)
A B C 1 D
【解析】
【考点】①变量散点图及运用;②函数模型定义与性质;③线性回归方程定义与性质;④求线性回归方程的基本方法。
【解题思路】根据函数模型和线性回归方程的性质,运用变量散点图和求线性回归方程的基本方法,结合问题条件求出的值就可得出选项。
【详细解答】=,z=lnx,=18,=z+1,===3,
=====2,1=-,
===1,C正确,选C。
3、下列命题中错误的是( )(成都市高2020级高三一诊)
A 在回归分析中,相关系数r的绝对值越大,两个变量的线性相关性越强 B 对分类变量X与Y,它们的随机变量的观测值k越小,说明“X与Y有关系”的把握性越大 C 线性回归直线=x+恒过点(,) D 在回归分析中,残差平方越小,模型的拟合效果越好
【解析】
【考点】①相关系数定义与性质;②判断两个随机变量线性相关的基本方法;③独立性检验定义与性质;④求线性回归方程的基本方法。
【解题思路】根据相关系数和独立性检验的性质,运用判断两个随机线性相关和求线性回归方程的基本方法,对各命题的真假进行判断就可得出选项。
【详细解答】对A,相关系数r的绝对值越大,两个变量的线性相关性越强,A正确,对B,对分类变量X与Y,它们的随机变量的观测值k越大,说明“X与Y有关系”的把握性越大,B错误;对C,=-,当x=时,=+-=, 线性回归直线=x+恒过点(,),C正确;对D, 在回归分析中,残差平方越小,模型的拟合效果越好,D正确, B错误,选B。
『思考问题4』
(2)【典例4】是判断两个随机变量相关关系和线性回归方程及运用的问题,解答这类问题需要理解两个随机变量相关和线性回归方程的定义,掌握判断两个随机变量是否具有相关关系和建立线性回归方程及回归分析的基本方法;
(2)判断两个随机变量是否相关的基本方法是:①根据数据作出随机变量的散点图,由散点图进行判断;②运用相关系数的计算公式,通过运算求出相关系数的值,根据相关系数值的大小进行判断;
(3)散点图法的基本方法是:①根据两个变量的一组对应值作出散点 图,②运用散点图判断两个随机变量是否具有相关关系;
(4)相关系数法的基本方法是:①根据两个变量的一组对应值运用公式计算相关系数的值,
②根据计算结果判断两个随机变量是否具有相关关系;
(7)判断两个变量是正相关还是负相关的常用方法是:①散点图法,②相关系数法,③运用线性回归方程=x+中的系数,若 > 0,为正相关;若 < 0为负相关。
(6)建立线性回归方程的基本方法是:①判断两个变量是否具有线性相关关系,②运用公式:
=, =- 求出回归系数,(也可以用待定系数法,即根据回归直线过样本点的中心求系数,),③写出回归直线方程;
(8)回归分析及回归预测的基本方法是:①依据回归直线方程视为变量y是变量x(或t)的一次函数,②将变量x(或t)的值代入回归直线方程求出变量y的值;③得出统计预测结果。
[练习4]解答下列问题:
1、某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:)的关系,在20个不同温度条件下进行种子发芽率实验,由实验数据(,)(i=1,2------,20)得到如下散点图:由此散点图,在10至40之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型是( )(2020全国高考新课标I)(答案:D)
A y=a+bx B y=a+b C y=a+b D y=a+blnx
2、某实验室对小白鼠体内x,y两项指标进行 小白鼠体内x 120 110 125 130 115
研究,连续五次实验所测得的这两项指标数据如 小白鼠体内y 92 83 90 96 89
表所示,已知y与x具有线性相关关系,利用表中数据求得回归直线方程为=x+,若下一次实验中x=170,利用该回归直线方程预测得=117,则的值为 (成都市2020
高三三诊)(答案:=0.54。)
【典例5】解答下列问题:
1、在某大学一食品超市,随机询问了70名不同性别 女 男 总计
的大学生在购买食物时是否查看营养说明,得到如下 要查看营养说明 15 25 40
的列联表:(成都市2019级高三三珍) 不查看营养说明 20 10 30
附:=其中n=a+b+c+d。 总计 35 35 70
P() 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005
0.455 0.708 1.323 2.702 2.706 3.841 5.024 6.635 7.879
根据列联表的独立性检验,则下列说法正确的是( )
A 在犯错误的概率不超过0.05的前提下,认为该校大学生在购买食物时要查看营养说明的人数中男生人数更多 B在犯错误的概率不超过0.010的前提下,认为该校大学生在购买食物时要查看营养说明的人数与不查看营养说明的人数比是 C 在犯错误的概率不超过0.025的前提下,认为性别与是否查看营养说明有关 D 在犯错误的概率不超过0.010的前提下,认为性别与是否查看营养说明有关
【解析】
【考点】①分类变量定义与性质;②列联表定义与性质;③独立性检验定义与性质;④随机变量计算公式及运用;⑤判断两个分类变量是否相关的基本方法。
【解题思路】根据分类变量,列联表和独立性检验的性质,运用计算随机变量的公式,结合问题条件求出随机变量的值,利用判断两个分类变量是否相关的基本方法,对该校大学生购买食物时,性别与是否查看营养说明的相关关系进行判断就可得出选项。
【详细解答】===5.833,5.024<5.833<6.635在犯错误的概率不超过0.025的前提下,认为性别与是否查看营养说明有关, C正确,选C。
『思考问题5』
(1)【典例5】是独立性检验的问题,解答这类问题需要理解分类变量,独立性检验的定义,了解2x2列联表的意义,掌握独立性检验的基本方法;
(2)比较两个分类变量是否有关的基本方法是:①计算的值进行判断,越大两个分类变量有关的可能性越大;②计算|ad-bc|的值进行判断,|ad-bc|越大两个分类变量有关的可能性越大;
(3)独立性检验的基本方法是:①根据样本数据制成2x2列联表,②运用公式=
计算的观察值,③比较与临界值的大小,作出推断。
【典例6】解答下列问题:
1、为了解推动出口后某收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后某收入的样本均值=2。1,样本方差=0.01,已知该种植区以往的某收入服从正态分布N(1.8,),假设推动出口后的某收入Y服从正态分布N(,),则( )(2024全国高考新高考I)(若随机变量Z服从正态分布N(u,),则p(Z<u+)0.8413)
A p(X>2)>0.2 B p(X>2)<0.5 C p(X>2)>0.5 D p(X>2)<0.8
【解析】
【考点】①随机变量正态分布定义与性质;②随机变量正态分布图像及运用。
【解题思路】根据随机变量正态分布的性质,运用随机变量正态分布的图像,结合问题条件求出p(X>2)的值就可得出选项。
【详细解答】该种植区以往的某收入服从正态分布N(1.8,),u=1.8,=0,1, p(Z<u+)0.8413, p(Z>u+)=1- p(Z<u+)1-0.84130.1587,p(X>2)= p(Z>u+2)<p(Z>u+)0.1587,B正确;推动出口后的某收入Y服从正态分布N(2.1,0。01),u=2.1,=0,1, p(Z<u+)0.8413, p(X>2)= p(Z>u-)= p(Z<u+)0.8413,C正确,综上所述,B,C正确,选B,C。
2、随机变量X服从正态分布N(2,),若p(22.5)= (2022全国高考新高考II卷)
【解析】
【考点】①随机变量正态分布定义与性质;②随机变量正态分布图像及运用。
【解题思路】根据随机变量正态分布的性质,运用随机变量正态分布的图像,结合问题条件就可求出p(X>2.5)的值。
【详细解答】随机变量X服从正态分布N(2,),p(22.5)=0.5- p(2『思考问题6』
(1)【典例6】是与正太分布相关的问题,解答这类问题需要理解正太曲线,正太分布的定义,了解正太曲线的性质,掌握正太分布下概率计算的基本方法;
(2)正太曲线的主要性质是:①曲线在x轴的上方,且与x轴不相交;②正态曲线的图像关于直线x=u对称;③曲线在x=u时达到高峰值,由这一点向左,右两边延伸时,曲线逐渐降低;
(3)正太变量在(-∞,+∞)内取值的概率是1,对于固定的u,来说,随机变量在(u-,u+)上的取值的概率随着的减小而增大,即越小,随机变量X取值落在(u-,u+)的概率越大。
[练习6]解答下列问题:
1、某物理量的测量结果服从正太分布N(10,),下列结论中不正确的是( )(2021全国高考新高考II)(答案:D)
A 越小,该物理量在一次测量中在(9.9,10.1)的概率越大 B 越小,该物理量在一次测量中大于10的概率为0.5 C 越小,该物理量在一次测量中小于9.99与大于10.01的概率相等 D 越小,该物理量在一次测量中落在(9.9,10.2)与落在(10,10.3)的概率相等
统计问题是近几年高考的热点内容之一。可以这样毫不夸张地说,只要是高考试卷,就必然涉及统计问题。从题型上看,可能是选择题(或填空题),也可能是大题,这里主要探导统计的5分小题问题;难度系数为低(或中)档。纵观近几年高考(或高三诊断考试)试卷,归结起来统计问题主要包括:①统计抽样的基本方法及运用;②统计表和统计图及运用;③统计指标计算及运用;④两个随机变量之间的相关关系及运用;⑤线性回归方程和独立性检验等几种类型。各种类型问题结构上具有一定的特征,解答方法也有一定的规律可寻。那么在实际解答统计5分小题问题时,到底应该如何抓住问题的结构特征,快捷,准确的解答问题呢?下面通过近几年高考(过高三诊断考试)试题的详细解析来回答这个问题。
【典例1】解答下列问题:
1、普法知识宣传小组打算从某小区的2000人中抽取25人进行法律知识培训,拟采取系统抽样方式,为此将他们一一编号为1-2000,并对编号由小到大进行分段,假设从第一个号码段中随机抽取的号码是2,那么从第三个号码段中抽出的号码为( ) (成都市高2021级高三一诊)
A 52 B 82 C 162 D 252
2、某区域有大型城市18个,中型城市12个,小型城市6个,为了解该区域城市空气质量情况,现采用分层抽样的方法抽取6个城市进行调查,则应抽取的大型城市的个数为 (成都市2019级高三二诊)
3、为了加强全民爱眼意识,提高民簇健康素质,1996年,卫生部,教育部,团中央等12个部委联合发出通知,将爱眼日活动列为国家节日之一,并确定每年的6月6日为“全国爱眼日”,某校高二(1)班有40名学生,学号为01到40,线采用随机数表法从该班抽取5名学生参加“全国爱眼日”宣传活动,已知随机数表中第六行至第七行的各数如下:
4、若从随机数表第6行第9列的数开始向右读,则抽取的第5名学生的学号是( )(成都市2021高三零诊)
A 17 B 23 C 35 D 37
5、某中学有高中生1500人,初中生1000人,为了解该校学生自主锻炼的时间,采用分层抽样的方法从高中学生和初中学生中抽取一个容量为n的样本,若样本中高中学生恰有30人则n的值为( )(成都市2020高三二诊)
A 20 B 50 C 40 D 60
6、下列抽样方法是简单随机抽样方法的是( )
A在某年明信片的销售活动中,规定每100万张为一个开奖组,通过随机抽取的方式确定号码的后四位为2700的为三等奖;B某车间包装一种产品,在自动包装的传送带上,每隔30分钟抽取一包产品,称其重量是否合格;C某学校分别从行政人员,教师,后勤人员抽取2人,14人,4人了解对学校机构改革的意见;D用抽签的方法从10件从产品中抽取3件进行质量检验。
『思考问题1』
(1)【典例1】是统计抽样基本方法及运用的问题,解答这类问题需要理解简单随机抽样,系统抽样和分层抽样的定义,了解简单随机抽样,系统抽样和分层抽样的特征与适用范围,掌握简单随机抽样,系统抽样和分层抽样的基本方法;
(2)运用抽签法必须注意两个基本条件:①抽签是否方便,②号签是否容易搅匀,一般地当总体容量和样本容量较小时可以采用抽签法;
(3)运用随机数表时,若遇到三位数或四位数,可以选择随机数表中某行某列的数字计起,每三个(或四个)作为一个单位,自左向右选取,有超过总体号码或重复号码舍去;
(4)系统抽样的特征是:①总体容量较大,②样本容量较大,③总体中各个个体之间没有明显的差异,④每个个体被抽到的可能性相等;
(5)系统抽样的基本方法是:①将总体中的个体进行统一编号,②把总体平均分成若干个部分(若总体容量不能被样本容量整除时,可以将总体随机剔除几个个体来确定分段间隔),③在第一个部分用简单随机抽样的方法确定开始的个体编号x,④按照每一组的个体数确定个体之间相隔的距离抽取样本;
(6)分层抽样的特征是:①总体容量较大,②总体由几个个体差异明显的部分构成;
(7)各层样本单位数的确定可按公式:某层抽取的样本数=样本数,通过计算来确定。
[练习1]解答下列问题:
1、某单位有840名职工,现采用系统抽样方法抽取42人做问卷调查,将840人按1,2,------,840随机编号,则抽取的42人中,编号落在区间[481,720]的人数为( )
A 11 B 12 C 13 D 14
2、将参加夏令营的600名学生编号为001,002,-------,600,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的号码为003,这600名学生分住在三个营区,从001到300在第I营区,从301到495在第II营区,从496到600在第III营区,三个营区被抽中的人数依次为( )
A 26,16,8 B 25,17,8 C 25,16,9 D 24,17,9
【典例2】解答下列问题:
1、“数九”从每年“冬至”当天开始计算,每九天为一个单位,冬至后的第81天,“数九”结束,天气九变得温暖起来。如图,以温江国家基准气象站为代表记录了20232024从“一九”到“九九”成都市的“平均气温”和“多年平均气温”(单位:),下列说法正确的是( )(成都市高2021级高三三诊)
A “四九”以后成都市“平均气温” 一直上升
B “四九”成都市“平均气温”较“多年平均气温”低0.1
C “一九” 到“五九” 成都市“平均气温” 的方差小于“多年平均气温”的方差
D “一九” 到“九九” 成都市“平均气温” 的极差小于“多年平均气温”的极差
1、全国文明典范城市是以全国文明城市为基础的文明城市典范,是城市治理“桂冠上的明珠”,为争创全国文明典范城市,某城市特邀请甲,乙两组评委分表从公共服务,文化建设,社会治理等10个不同维度对城市建设进行评分,每个维度满分为10分,现将两组评委的评分制成如图所示的茎叶图,其中茎叶图中茎部分是得分的个位数,叶部分是得分的小数,则下列结论中正确的是( )(成都市高2021级高三零诊)
A 甲组评分的平均数小于乙组评分的平均数 B 甲,乙两组评分的中位数不相同
C 甲组评分的极差大于乙组评分的极差 D 甲组评分的众数小于乙组评分的众数
2、从某小区随机抽取100户居民用户进行月用电量调查,发现他们的月用电量 50—300kw.h之间,适当分组(每组为左闭右开区间)后绘制成如图所示的频率分布直方图,则直方图中x的值以及在被调查的用户约用电量落在区间[100,250)内的户数分布为( )(成都市2020级高三零诊)
A 0.0046 ,72 B 0.0046,70 C 0.0042 ,72 D 0.0042 ,70
甲 乙
3、分别统计了甲,乙两位同学16周的各周 6 1 5
课外体育运动时长(单位:h),得到如表所 8 5 3 0 6 3
示的茎叶图: 7 5 3 2 7 4 6
则下列结论中错误的是( )(2022全国高考 6 4 2 1 8 1 2 2 5 6 6 6 6
乙卷文) 4 2 9 0 2 3 8
A 甲同学周课外体育运动时长的样本中位数为7.4 10 1 B 乙同学周课外体育运动时长的样本平均数大于8 C 甲同学周课外体育运动时长大于8的概率的估计值大于0.4 D 乙同学周课外体育运动时长大于8的概率的估计值大于0.6
4、为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )(2021全国高考甲卷)
A该地农户家庭年收入低于4.5万元的农户比率估计为6%
B该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C估计该地农户家庭年收入的平均值不超过6.5万元
D根据该地有一半以上农户,其家庭年收入介于4.5万元至8.5万元之间
5、如图,是某赛季甲,乙两名篮球运动员9场比赛 甲 乙
所得分数的茎叶图,则下列说法错误的是( )(20 0 8
20成都市高三零诊)A 甲所得分数的极差为22 B 7 5 1 1 1 2 6 8
乙所得分数的中位数为18 C 两人所得分数的众数相 4 2 2 0 2 0 2 2
等D 甲所得分数的平均数低于乙所得分数的平均数 3 2 3 1
6、某校随机抽取100名同学进行“垃圾分类”的问卷测试,测试结果发现这100名同学的得分都在[50,
100]内,按得分分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图,则这100名同学得分的中位数为( )(2020成都市高三一诊)
A 72.5 B 75 C 77.5 D 80
『思考问题2』
(1)【典例2】是统计表和统计图及运用的问题,解答这类问题需要理解统计表,茎叶图和频率分布直方图的定义,掌握制作统计表,茎叶图和频率分布直方图的基本作法,注意统计表,茎叶图和频率分布直方图的运用;
(2)茎叶图的特征是:①茎叶图能够看到真实的数据,没有任何信息损失;②茎叶图便于记录和表示;③茎叶图只便于表示两位有效数字的数据;④茎叶图也只方便记录两组数据;
(3)茎叶图的基本画法是:①用两短竖线把图分成两个部分;②两组数据中选一组放左边,另一组放右边;③把数据的十位数记在两短竖线之间;④将数据的个位数分别记在左右两边;
(4)解答与频率分布直方图相关问题的关键是读懂频率分布直方图,频率分布直方图中的每一个小矩形的面积是指样本数据落在该区域的频率,所有小矩形面积的和为1;
(5)作频率分布直方图的基本方法是:①求出原始数据的极差(最大值与最小值的差);②确定组数与组距;③确定各组的起始点与终点;④列出统计数据分布表;⑤画出频率分布直方图;
【典例3】解答下列问题:
1、某农业研究部门在面积相等的100块稻田种植一种新型水稻,得到各块稻田的亩产量(单位:千克)并整理如下表:
亩产量[900,950)[950,1000)[1000,1050)[1050,1100 )[1100,1150)[1150,
频数 6 12 18 30 24 10
根据表中数据,下列结论正确的是( )(2024全国高考新高考II)
A 100块稻田亩产量的中位数是1050千克
B 100块稻田亩产量低于1100千克的稻田所占比例超过80%
C 100块稻田亩产量的极差介于200千克到300千克之间
D 100块稻田亩产量的平均值介于900千克到1000千克之间
2、有一组样本数据:,,------,,其中是最小值,是最大值,其平均数为,方差为,极差为m,中位数为t,去除其中的最小值和最大值后,余下数据的平均数为,方差为,极差为,中位数为,则下列结论不一定正确的是( )(2023全国高考新高考I)
A ,,, 的平均数等于,,------,的平均数 B ,,, 的中位数等于,,------,的中位数 C ,,, 的标准差不小于,,------,的标准差 D ,,, 的极差不大于,,------,的极差
3、下图为2012年-2021年我国电子信息制造业企业和工业企业利润总额增速情况折线图,根据该图,下列结论正确的是( ) (成都市高2020级高三一诊)
A 2012年-2021年电子信息制造业企业利润总额逐年递增 B 2012年-2021年工业企业利
润总额逐年递增 C 2012年-2017年电子信息制造业企业利润总额均比上一年实现增长,且其增速快于当年工业企业利润总额增速 D 2012年-2021年工业企业利润总额增速的均值大于递增信息制造业企业利润总额增速均值
4、一次数学考试后,某班级平均分为110分,方差为,现发现有两名同学的成绩计算有误,甲同学成绩被误判为113分,实际得分为118分,乙同学成绩被误判为120分,实际成绩为115分,更正后重新计算,得到方差为,则与的大小关系为( )(成都市高2020级高三三珍)
A = B > C < D 不能确定
5、(理)若数据9,m,6,n,5的平均数为7,方差为2,则数据11,9,2m-1,17,2n-1的平均数和方差分别为( )
A 13,4 B 14,4 C 13,8 D 14,8
(文)若数据9,m,6,5的平均数为7,则数据17, 2m-1,11,9的平均数和方差分别为( )(成都市2020级高三零诊)
A 13,5 B 14,5 C 13,10 D 14,10
6、某地区通过公益讲座以及普及社区居民的垃圾分类知识,为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如下图:则( )(2022全国高考甲卷)
A讲座前问卷答题的正确率的中位数小于70%
B讲座后问卷答题的正确率的平均数大于85%
C讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D 讲座后问卷答题的正确率的极差大于讲座前正确率的极差
7、四名同学各掷骰子5次,并各自记录每次骰子出现的点数,分别统计四名同学的纪录结果,可以判断出一定没有出现点数6的是( )(成都市2019级高三一诊)
A 平均数为3,中位数为2 B 中位数为3,众数为2
C 中位数为3,方差为2.8 D 平均数为2,方差为2.4
8、有一组样本数据,,------,,由这组数据得到新样本数据,,-------,,其中=+c(i=1,2,-----,n),c为非零常数,则( )(2021全国高考新高考I)
A 两组样本数据的样本平均数相同 B 两组样本数据的样本中位数相同
C 两组样本数据的样本标准差相同 D 两组样本数据的样本极差相同
『思考问题3』
(1)【典例3】是统计指标及运用的问题,解答这类问题需要理解平均数,方差,标准差的定义,掌握求平均数,方差,标准差的基本求法;
(2)总体估计的常用方法有:①点估计;②区间估计;
(3)点估计是直接运用样本指标作为总体指标,常用的样本指标有:①样本的平均数;②样本的标准差;③样本的方差;常用的总体指标有:①总体的平均数;②总体的标准差;③总体的方差;
(4)区间估计是根据问题要求可靠程度去确定总体指标取值的区间,其基本方法是:①由问题要求的可靠程度确定抽样的平均误差;②根据抽样平均误差确定抽样误差的允许范围;③根据抽样误差的允许范围确定总体指标的取值范围。
[练习3]解答下列问题:
1、下列统计量中,能度量样本,,------,的离散程度的是( )
A 样本,,------,的标准差 B 样本,,------,的中位数
C 样本,,------,的极差 D 样本,,------,的平均数
2、甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是:,分别表示甲乙
甲 0 1 0 2 2 0 3 1 2 4
乙 2 2 1 1 1 2 1 1 0 1
两组数据的平均数,,分别表示甲乙两组数据的方差,则下列选项正确的是( )(成都市2021高三一诊)
A = ,> B >,> C <,< D >,<
3、某市环境保护局公布了该市A,B两个景区2014年至2020年各年的全年空气质量优良天数的数据,现根据这些数据绘制了如图所示的折线图,则由该折线图得出的下列结论中正确的是( )(成都市2021高三三诊)
A 景区A这7年的空气质量优良天数的极差为98 B 景区B这7年的空气质量优良天数的中位数为283 C 分别记景区A,B这7年的空气质量优良天数的众数为,,则>
D分别记景区A,B这7年的空气质量优良天数的标准差为 ,,则 >
4、(理)在一组样本数据中,1,2,3,4出现的频率分别为,,,,且=1,
则下列四种情形中,对应样本的标准差最大的一组是( )
A ==0.1,==0.4 B ==0.4,==0.1
C ==0.2,==0.3 D ==0.3,==0.2
(文)设一组样本数据,,-------,的方差为0.01,则数据10,10,-------,10的方差为( )(2020全国高考新课标III)
A 0.01 B 0.1 C 1 D 10
【典例4】解答下列问题:
1、 对变量x,y有观测数据(,)(i),得散点图1;对变量u,v有观测数据(,
)(i)得散点图2,表示变量x,y之间的线性相关系数,表示变量u,v之间的线性相关系数,则下列说法正确的是( )(成都市高2021级高三二诊)
A 变量x,y呈正相关,且||<|| B 变量x,y呈负相关,且||>||
C 变量x,y呈正相关,且||>|| D 变量x,y呈负相关,且||<||
2、 如图,由观察数据(,)(i=1,2,3,4,5,6)的散点图可知,y与x的关系可以
用模型y=blnx+a拟合,设z=lnx,利用最小二乘法求得y关于z的回归方程=z+1,已知=,=18,则=( )(成都市高2021级高三三诊)
A B C 1 D
3、下列命题中错误的是( )(成都市高2020级高三一诊)
A 在回归分析中,相关系数r的绝对值越大,两个变量的线性相关性越强 B 对分类变量X与Y,它们的随机变量的观测值k越小,说明“X与Y有关系”的把握性越大 C 线性回归直线=x+恒过点(,) D 在回归分析中,残差平方越小,模型的拟合效果越好
『思考问题4』
(1)【典例4】是判断两个随机变量相关关系和线性回归方程及运用的问题,解答这类问题需要理解两个随机变量相关和线性回归方程的定义,掌握判断两个随机变量是否具有相关关系和建立线性回归方程及回归分析的基本方法;
(2)判断两个随机变量是否相关的基本方法是:①根据数据作出随机变量的散点图,由散点图进行判断;②运用相关系数的计算公式,通过运算求出相关系数的值,根据相关系数值的大小进行判断;
(3)散点图法的基本方法是:①根据两个变量的一组对应值作出散点 图,②运用散点图判断两个随机变量是否具有相关关系;
(4)相关系数法的基本方法是:①根据两个变量的一组对应值运用公式计算相关系数的值,
②根据计算结果判断两个随机变量是否具有相关关系;
(5)判断两个变量是正相关还是负相关的常用方法是:①散点图法,②相关系数法,③运用线性回归方程=x+中的系数,若 > 0,为正相关;若 < 0为负相关。
(6)建立线性回归方程的基本方法是:①判断两个变量是否具有线性相关关系,②运用公式:
=, =- 求出回归系数,(也可以用待定系数法,即根据回归直线过样本点的中心求系数,),③写出回归直线方程;
(6)回归分析及回归预测的基本方法是:①依据回归直线方程视为变量y是变量x(或t)的一次函数,②将变量x(或t)的值代入回归直线方程求出变量y的值;③得出统计预测结果。
[练习4]解答下列问题:
1、某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:)的关系,在20个不同温度条件下进行种子发芽率实验,由实验数据(,)(i=1,2------,20)得到如下散点图:由此散点图,在10至40之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型是( )(2020全国高考新课标I)
A y=a+bx B y=a+b C y=a+b D y=a+blnx
2、某实验室对小白鼠体内x,y两项指标进行 小白鼠体内x 120 110 125 130 115
研究,连续五次实验所测得的这两项指标数据如 小白鼠体内y 92 83 90 96 89
表所示,已知y与x具有线性相关关系,利用表中数据求得回归直线方程为=x+,若下一次实验中x=170,利用该回归直线方程预测得=117,则的值为 (成都市2020
高三三诊)
【典例5】解答下列问题:
1、在某大学一食品超市,随机询问了70名不同性别 女 男 总计
的大学生在购买食物时是否查看营养说明,得到如下 要查看营养说明 15 25 40
的列联表:(成都市2019级高三三珍) 不查看营养说明 20 10 30
附:=其中n=a+b+c+d。 总计 35 35 70
P() 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005
0.455 0.708 1.323 2.702 2.706 3.841 5.024 6.635 7.879
根据列联表的独立性检验,则下列说法正确的是( )
A 在犯错误的概率不超过0.05的前提下,认为该校大学生在购买食物时要查看营养说明的人数中男生人数更多 B在犯错误的概率不超过0.010的前提下,认为该校大学生在购买食物时要查看营养说明的人数与不查看营养说明的人数比是 C 在犯错误的概率不超过0.025的前提下,认为性别与是否查看营养说明有关 D 在犯错误的概率不超过0.010的前提下,认为性别与是否查看营养说明有关
『思考问题5』
(1)【典例5】是独立性检验的问题,解答这类问题需要理解分类变量,独立性检验的定义,了解2x2列联表的意义,掌握独立性检验的基本方法;
(2)比较两个分类变量是否有关的基本方法是:①计算的值进行判断,越大两个分类变量有关的可能性越大;②计算|ad-bc|的值进行判断,|ad-bc|越大两个分类变量有关的可能性越大;
(3)独立性检验的基本方法是:①根据样本数据制成2x2列联表,②运用公式= 计算的观察值,③比较与临界值的大小,作出推断。
【典例6】解答下列问题:
1、为了解推动出口后某收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后某收入的样本均值=21,样本方差=0.01,已知该种植区以往的某收入服从正态分布N(1.8,),假设推动出口后的某收入Y服从正态分布N(,),则( )(2024全国高考新高考I)(若随机变量Z服从正态分布N(1u,),则p(Z<u+)0.8413)
A p(X>2)>0.2 B p(X>2)<0.5 C p(X>2)>0.5 D p(X>2)<0.8
2、随机变量X服从正态分布N(2,),若p(2
『思考问题6』
(1)【典例6】是与正太分布相关的问题,解答这类问题需要理解正太曲线,正太分布的定义,了解正太曲线的性质,掌握正太分布下概率计算的基本方法;
(2)正太曲线的主要性质是:①曲线在x轴的上方,且与x轴不相交;②正态曲线的图像关于直线x=u对称;③曲线在x=u时达到高峰值,由这一点向左,右两边延伸时,曲线逐渐降低;
(3)正太变量在(-∞,+∞)内取值的概率是1,对于固定的u,来说,随机变量在(u-,u+)上的取值的概率随着的减小而增大,即越小,随机变量X取值落在(u-,u+)的概率越大。
[练习6]解答下列问题:
1、某物理量的测量结果服从正太分布N(10,),下列结论中不正确的是( )(2021全国高考新高考II)
A 越小,该物理量在一次测量中在(9.9,10.1)的概率越大 B 越小,该物理量在一次测量中大于10的概率为0.5 C 越小,该物理量在一次测量中小于9.99与大于10.01的概率相等 D 越小,该物理量在一次测量中落在(9.9,10.2)与落在(10,10.3)的概率相等
高考试题中统计5分小题问题的类型与解法
统计问题是近几年高考的热点内容之一。可以这样毫不夸张地说,只要是高考试卷,就必然涉及统计问题。从题型上看,可能是选择题(或填空题),也可能是大题,这里主要探导统计的5分小题问题;难度系数为低(或中)档。纵观近几年高考(或高三诊断考试)试卷,归结起来统计问题主要包括:①统计抽样的基本方法及运用;②统计表和统计图及运用;③统计指标计算及运用;④两个随机变量之间的相关关系及运用;⑤线性回归方程和独立性检验等几种类型。各种类型问题结构上具有一定的特征,解答方法也有一定的规律可寻。那么在实际解答统计5分小题问题时,到底应该如何抓住问题的结构特征,快捷,准确的解答问题呢?下面通过近几年高考(过高三诊断考试)试题的详细解析来回答这个问题。
【典例1】解答下列问题:
1、 普法知识宣传小组打算从某小区的2000人中抽取25人进行法律知识培训,拟采取系统抽
样方式,为此将他们一一编号为1-2000,并对编号由小到大进行分段,假设从第一个号码段中随机抽取的号码是2,那么从第三个号码段中抽出的号码为( ) (成都市高2021级高三一诊)
A 52 B 82 C 162 D 252
【解析】
【考点】①系统抽样法定义与性质;②系统抽样法的基本方法。
【解题思路】根据系统抽样法的性质,运用系统抽样法的基本方法,结合问题条件求出从第三个号码段中抽出的号码就可得出选项。
【详细解答】=80,第一个号码段中随机抽取的号码是2, 从第三个号码段中抽出的号码为162,C正确,选C。
2、某区域有大型城市18个,中型城市12个,小型城市6个,为了解该区域城市空气质量情况,现采用分层抽样的方法抽取6个城市进行调查,则应抽取的大型城市的个数为 (成都市2019级高三二诊)
【解析】
【考点】①分层抽样方法定义与性质;②求分层抽样方法中每层抽取数的基本方法。
【解题思路】根据分层抽样的性质,运用求分层抽样方法中每层抽取数的基本方法就可求出应抽取的大型城市的个数。
【详细解答】该区域有大型城市18个,中型城市12个,小型城市6个,用分层抽样的方法抽取6个城市, 应抽取的大型城市的个数为6=6=3(个 )。
3、为了加强全民爱眼意识,提高民簇健康素质,1996年,卫生部,教育部,团中央等12个部委联合发出通知,将爱眼日活动列为国家节日之一,并确定每年的6月6日为“全国爱眼日”,某校高二(1)班有40名学生,学号为01到40,现采用随机数表法从该班抽取5名学生参加“全国爱眼日”宣传活动,已知随机数表中第六行至第七行的各数如下:若从第六行
的第十列开始,由左向右依次选取两个数字,则抽取到的第五名学生的编号为( )
A 20 B 17 C 37 D 23
【解析】
【考点】①随机数表定义与性质;②运用随机数表抽样的基本方法。
【解题思路】根据分层抽样的性质,运用求分层抽样方法中每层抽取数的基本方法就可求出应抽取的大型城市的个数。
【详细解答】采用随机数表法,且从第六行的第十列开始,抽取的5名学生的编号分别为17,37,23,35,20,抽取到的第五名学生的编号为20,A正确,选A。
4、若从随机数表第6行第9列的数开始向右读,则抽取的第5名学生的学号是( )(成都市2021高三零诊)
A 17 B 23 C 35 D 37
【解析】
【考点】①随机数表法抽样的定义与性质;②随机数表法抽样的基本方法。
【解题思路】根据随机数表法抽样的性质和随机数表法抽样的基本方法,结合问题条件确定出第5名学生的学号就可得出选项。
【详细解答】抽样是从随机数表第6行第9列的数开始向右读, 第1名学生的学号为39,第2名学生的学号为17,第3名学生的学号为37,第4名学生的学号为23,第5名学生的学号为35,C错误,选C。
5、某中学有高中生1500人,初中生1000人,为了解该校学生自主锻炼的时间,采用分层抽样的方法从高中学生和初中学生中抽取一个容量为n的样本,若样本中高中学生恰有30人,则n的值为( )(成都市2020高三二诊)
A 20 B 50 C 40 D 60
【解析】
【考点】①样本容量定义与性质;②分层抽样定义与性质;③分层抽样各层抽样数的计算公式及运用;④计算分层抽样各层抽样数的基本方法。
【解题思路】根据分层抽样的性质,运用分层抽样各层抽样数的计算公式,结合问题条件得到关于n的方程,求解方程求出样本容量n的值就可得出选项。
【详细解答】n=30, n=30=50, B正确,选B。
6、下列抽样方法是简单随机抽样方法的是( )
A在某年明信片的销售活动中,规定每100万张为一个开奖组,通过随机抽取的方式确定号码的后四位为2700的为三等奖;B某车间包装一种产品,在自动包装的传送带上,每隔30分钟抽取一包产品,称其重量是否合格;C某学校分别从行政人员,教师,后勤人员抽取2人,14人,4人了解对学校机构改革的意见;D用抽签的方法从10件从产品中抽取3件进行质量检验。
【解析】
【知识点】①简单随机抽样的定义与性质;②简单随机抽样的基本方法。
【解题思路】运用简单随机抽样的性质和简单随机抽样的基本方法,对各选项进行判断就可得出选项。
【详细解答】对A,在100万张明信片中,后四位为2700的明信片每一万张中就有一张,属于系统抽样,A不正确;对B,在自动包装的传送带上,每隔30分钟抽取一包产品,属于等距抽样, B不正确;对C,分别从行政人员,教师,后勤人员抽取2人,14人,4人属于分层抽样, C不正确;对D,用抽签的方法从10件从产品中抽取3件符合简单随机抽样的特征, D正确,即选D。
『思考问题1』
(1)【典例1】是统计抽样基本方法及运用的问题,解答这类问题需要理解简单随机抽样,系统抽样和分层抽样的定义,了解简单随机抽样,系统抽样和分层抽样的特征与适用范围,掌握简单随机抽样,系统抽样和分层抽样的基本方法;
(2)运用抽签法必须注意两个基本条件:①抽签是否方便,②号签是否容易搅匀,一般地当总体容量和样本容量较小时可以采用抽签法;
(3)运用随机数表时,若遇到三位数或四位数,可以选择随机数表中某行某列的数字计起,每三个(或四个)作为一个单位,自左向右选取,有超过总体号码或重复号码舍去;
(4)系统抽样的特征是:①总体容量较大,②样本容量较大,③总体中各个个体之间没有明显的差异,④每个个体被抽到的可能性相等;
(5)系统抽样的基本方法是:①将总体中的个体进行统一编号,②把总体平均分成若干个部分(若总体容量不能被样本容量整除时,可以将总体随机剔除几个个体来确定分段间隔),③在第一个部分用简单随机抽样的方法确定开始的个体编号x,④按照每一组的个体数确定个体之间相隔的距离抽取样本;
(6)分层抽样的特征是:①总体容量较大,②总体由几个个体差异明显的部分构成;
(7)各层样本单位数的确定可按公式:某层抽取的样本数=样本数,通过计算来确定。
[练习1]解答下列问题:
1、某单位有840名职工,现采用系统抽样方法抽取42人做问卷调查,将840人按1,2,------,840随机编号,则抽取的42人中,编号落在区间[481,720]的人数为( )(答案:B)
A 11 B 12 C 13 D 14
2、将参加夏令营的600名学生编号为001,002,-------,600,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的号码为003,这600名学生分住在三个营区,从001到300在第I营区,从301到495在第II营区,从496到600在第III营区,三个营区被抽中的人数依次为( )(答案:B)
A 26,16,8 B 25,17,8 C 25,16,9 D 24,17,9
【典例2】解答下列问题:
1、“数九”从每年“冬至”当天开始计算,每九天为一个单位,冬至后的第81天,“数九”结束,天气九变得温暖起来。如图,以温江国家基准气象站为代表记录了20232024从“一九”到“九九”成都市的“平均气温”和“多年平均气温”(单位:),下列说法正确的是( )(成都市高2021级高三三诊)
A “四九”以后成都市“平均气温” 一直上升
B “四九”成都市“平均气温”较“多年平均气温”低0.1
C “一九” 到“五九” 成都市“平均气温” 的方差小于“多年平均气温”的方差
D “一九” 到“九九” 成都市“平均气温” 的极差小于“多年平均气温”的极差
【解析】
【考点】①平均数定义与性质;②方差定义与性质;③极差定义与性质;④统计直方图及运
用;⑤求一组数据平均数的基本方法;⑥求一组数据方差的基本方法;⑦求一组数据极差的基本方法。
【解题思路】根据平均数,方差和极差的性质,运用统计直方图和求一组数列平均数,方差与极差的基本方法,结合问题条件对各选项说法的正确与错误进行判断就可得出选项。
【详细解答】对A,从条件直方图可知,“八九”的“平均气温”比“七九”的“平均气温”低,A错误;对B,从条件直方图可知,“四九”的“平均气温”比“多年平均气温”高0.1,B错误;对C,从“一九” 到“五九” 成都市“平均气温”的平均数为==6.96(),成都市“多年平均气温”的平均数为==5.62(),成都市“平均气温”的方差为
==3.15536,成都市“多年平均气温”的方差数为==0.1350,>,C错误;对D,从“一九” 到“五九” 成都市“平均气温”的极差为10.6-5.4=5.2(), 成都市“多年平均气温”的极差为10.7-5.3=5.4(),5.2<5.4,D正确,综上所述D正确,选D。
2、全国文明典范城市是以全国文明城市为基础的文明城市典范,是城市治理“桂冠上的明珠”,为争创全国文明典范城市,某城市特邀请甲,乙两组评委分表从公共服务,文化建设,社会治理等10个不同维度对城市建设进行评分,每个维度满分为10分,现将两组评委的评分制成如图所示的茎叶图,其中茎叶图中茎部分是得分的个位数,叶部分是得分的小数,则下列结论中正确的是( )(成都市高2021级高三零诊)
A 甲组评分的平均数小于乙组评分的平均数 B 甲,乙两组评分的中位数不相同
C 甲组评分的极差大于乙组评分的极差 D 甲组评分的众数小于乙组评分的众数
【解析】
【考点】①茎叶图定义与性质;②数据平均数定义与性质;③数据中位数定义与性质;④数据极差定义与性质;⑤数据众数定义与性质。
【解答思路】根据茎叶图,数据平均数,中位数,极差和众数的性质,运用茎叶图的数据分别求出甲组,乙组评分的平均数,中位数,极差和众数,对各选项结论的正确与错误进行判断就可得出选项。
【详细解答】对A,==8.06,
==8.16,8.06<8.16, A正确;
对B, 甲组评委评分的中位数为=8.05,,乙组评委评分的中位数为
=8.05,8.05=8.05,B错误;对C, 甲组评委评分的极差为8.6-7.5=1.1,,乙组评委评分的极差为9.8-7.5=23,1.1<2.3,C错误;对D, 甲组评委评分的众数为8.3,,乙组评委评分的众数为7.8,8.3>7.8,D错误,综上所述A正确,选A。
3、从某小区随机抽取100户居民用户进行月用电量调查,发现他们的月用电量 50—300kw.h
之间,适当分组(每组为左闭右开区间)后绘制成如图所示的频率分布直方图,则直方图中x的值以及在被调查的用户约用电量落在区间[100,250)内的户数分布为( )(成都市2020级高三零诊)
A 0.0046 ,72 B 0.0046,70 C 0.0042 ,72 D 0.0042 ,70
【解析】
【考点】①频率分布直方图定义与性质;②频率定义与性质;③确定某一区间数据的基本方法。
【解答思路】根据频率分布直方图和频率的性质,求出x的值和区间[100,250)的频率,从而求出用电量落在区间[100,250)内的户数,就可得出选项。
【详细解答】由频率分布直方图可知,50(0.0024+0.0032+0.0038+x+0.0060)=50(0.0154
+x)=1, x=0.02-0.0154=0.0046, 用电量落在区间[100,250)内的频率为50(0.0038
0.0046+0.0060)=0.72,用电量落在区间[100,250)内的户数为1000.72=72(户),A正确,选A。 甲 乙
4、分别统计了甲,乙两位同学16周的各周 6 1 5
课外体育运动时长(单位:h),得到如表所 8 5 3 0 6 3
示的茎叶图: 7 5 3 2 7 4 6
则下列结论中错误的是( )(2022全国高考 6 4 2 1 8 1 2 2 5 6 6 6 6
乙卷文) 4 2 9 0 2 3 8
A 甲同学周课外体育运动时长的样本中位数为7.4 10 1 B 乙同学周课外体育运动时长的样本平均数大于8 C 甲同学周课外体育运动时长大于8的概率的估计值大于0.4 D 乙同学周课外体育运动时长大于8的概率的估计值大于0.6
【解析】
【考点】①茎叶图定义与性质;②中位数定义与求法;③平均数定义与求法;④统计估计的基本方法。
【解题思路】根据茎叶图的性质,运用求中位数和平均数的基本方法,结合问题条件分别求出甲同学周课外体育运动时长的样本中位数和乙同学周课外体育运动时长的样本平均数,利
用统计估计的基本方法,分别估计出甲同学周课外体育运动时长大于8的概率和乙同学周课外体育运动时长大于8的概率就可得出选项。
【详细解答】甲同学周课外体育运动时长的样本中位数为=7.4,乙同学周课外体育运动时长的样本平均数为
=8.50625>8,甲同学周课外体育运动时长大于8的概率的估计值为=0.375<0.4,乙同学周课外体育运动时长大于8的概率的估计值为=0.8125>0.8,C结论不正确,选C。
5、为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )(2021全国高考甲卷)
A该地农户家庭年收入低于4.5万元的农户比率估计为6%
B该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C估计该地农户家庭年收入的平均值不超过6.5万元
D根据该地有一半以上农户,其家庭年收入介于4.5万元至8.5万元之间
【解析】
【考点】①频率分布直方图的定义与性质;②频率的定义与基本求法;③统计估计的基本方法;④平均数计算公式及运用。
【解题思路】根据样频率分布直方图的性质和求频率的基本方法,结合问题条件分别求出该地农户家庭年收入低于4.5万元的农户,低于10.5万元的农户和介于4.5万元至8.5万元之间的农户的频率,运用计算平均数的公式求出该地农户家庭年收入的平均值,利用统计估计的基本方法就可得出选项。
【详细解答】该地农户家庭年收入低于4.5万元的农户比率为(0.02+0.04)1
=0.06,A正确;该地农户家庭年收入低于10.5万元的农户比率(0.02+0.04+
0.13+0.14+0.202)1=0.90,该地农户家庭年收入不低于10.5万元的农户比率为1-0.90=0.10,即B正确;该地农户家庭年收入的平均值为0.02(3+12+13+14)+0.04(4+11)+0.10(5+9+10)+0.146+0.20(7+8)=7.68>6.5,C错误,C结论不正确,选C。
6、如图,是某赛季甲,乙两名篮球运动员9场比赛 甲 乙
所得分数的茎叶图,则下列说法错误的是( )(20 0 8
20成都市高三零诊)A 甲所得分数的极差为22 B 7 5 1 1 1 2 6 8
乙所得分数的中位数为18 C 两人所得分数的众数相 4 2 2 0 2 0 2 2
等D 甲所得分数的平均数低于乙所得分数的平均数 3 2 3 1
【解析】
【考点】①茎叶图的定义与性质;②极差的定义与求法;③中位数的定义与求法;④众数的定义与求法;⑤平均数的定义与求法。
【解题思路】运用茎叶图的性质,结合问题条件分别求出甲所得分数的极差,乙所得分数的
中位数,甲,乙所得分数的众数和平均数就可得出选项。
【详细解答】甲所得分数的极差为33-11=22,A正确;乙所得分数的中位数为18,B正确;甲,乙所得分数的众数分别为22,22,C正确;甲,乙所得分数的平均数分别为= 21.8,
= 17.8,21.8>17.8,>,D错误,选D。
『思考问题2』
(1)【典例2】是统计表和统计图及运用的问题,解答这类问题需要理解统计表,茎叶图和频率分布直方图的定义,掌握制作统计表,茎叶图和频率分布直方图的基本作法,注意统计表,茎叶图和频率分布直方图的运用;
(2)茎叶图的特征是:①茎叶图能够看到真实的数据,没有任何信息损失;②茎叶图便于记录和表示;③茎叶图只便于表示两位有效数字的数据;④茎叶图也只方便记录两组数据;
(3)茎叶图的基本画法是:①用两短竖线分成把图分成两部分,②两组数据中选一组放左边,另一组放右边,③把数据的十位数记在两短竖线之间,④将数据的个位数分别记在左右两边;
(4)解答与频率分布直方图相关问题的关键是读懂频率分布直方图,频率分布直方图中的每一个小矩形的面积是指样本数据落在该区域的频率,所有小矩形面积的和为1;
(5)作频率分布直方图的基本方法是:①求出原始数据的极差(最大值与最小值的差);②确定组数与组距;③确定各组的起始点与终点;④列出统计数据分布表;⑤画出频率分布直方图;
[练习2]解答下列问题:
1、某校随机抽取100名同学进行“垃圾分类”的问卷测试,测试结果发现这100名同学的得分都在[50,100]内,按得分分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图,则这100名同学得分的中位数为()(2020成都市高三一诊)
A 72.5 B 75 C 77.5 D 80
(答案:A)
【典例3】解答下列问题:
1、某农业研究部门在面积相等的100块稻田种植一种新型水稻,得到各块稻田的亩产量(单位:千克)并整理如下表:
亩产量[900,950)[950,1000)[1000,1050)[1050,1100 )[1100,1150)[1150,
频数 6 12 18 30 24 10
根据表中数据,下列结论正确的是( )(2024全国高考新高考II)
A 100块稻田亩产量的中位数是1050千克
B 100块稻田亩产量低于1100千克的稻田所占比例超过80%
C 100块稻田亩产量的极差介于200千克到300千克之间
D 100块稻田亩产量的平均值介于900千克到1000千克之间
【解析】
【考点】①中位数定义与性质;②极差定义与性质;③平均数定义与性质;④求一组数据,中位数,极差和平均数的基本方法。
【解题思路】根据平均数,中位数和极差的性质,运用求一组数据,中位数,极差和平均数的基本方法,结合问题条件对各选项结论的正确与错误进行判断就可得出选项。
【详细解答】对A,6+12+18=36<50,100块稻田亩产量的中位数大于1050,A错误;对B, 100块稻田亩产量低于1100千克的稻田所占比例为 100%=66%
<80%,B错误;对C,100块稻田亩产量的极差大于1150-950=200,小于1200-900=300,100块稻田亩产量的极差介于200千克到300千克之间,C正确;对D,100块稻田亩产量的平均值为(9256+97512+102518+107530+112524+117510)=1067>1000,
D错误,综上所述,C正确,选C。
2、有一组样本数据:,,------,,其中是最小值,是最大值,其平均数为,
方差为,极差为m,中位数为t,去除其中的最小值和最大值后,余下数据的平均数为,方差为,极差为,中位数为,则下列结论不一定正确的是( )(2023全国高考新高考I)
A ,,, 的平均数等于,,------,的平均数 B ,,, 的中位数等于,,------,的中位数 C ,,, 的标准差不小于,,------,的标准差 D ,,, 的极差不大于,,------,的极差
【解析】
【考点】①一组数据平均数定义与性质;②一组数据中位数定义与性质;③一组数据标准差定义与性质;④一组数据极差定义与性质。
【解题思路】根据一组数据平均数,中位数,标准差和极差的性质,结合问题条件确定出数据的平均数,中位数,标准差和极差就可得出选项。
【详细解答】设:,,------,,分别为1,2,2,2,2,4,对A,,,,
的平均数为2,,,------,的平均数为,A错误;对B,,,, 的中位数为=2,,,------,的中位数为=2,B正确;对C,,,, 的标准差为0,,,------,的标准差为=,C错误;对D,,,, 的极差为2-2=0,,,------,的极差为4-1=3,0≤3,D正确,综上所述B,D正确,选BD。
3、下图为2012年-2021年我国电子信息制造业企业和工业企业利润总额增速情况折线图,根据该图,下列结论正确的是( ) (成都市高2020级高三一诊)
A 2012年-2021年电子信息制造业企业利润总额逐年递增 B 2012年-2021年工业企业利
润总额逐年递增 C 2012年-2017年电子信息制造业企业利润总额均比上一年实现增长,且其增速快于当年工业企业利润总额增速 D 2012年-2021年工业企业利润总额增速的均值大于递增信息制造业企业利润总额增速均值
【解析】
【考点】①统计折线图平定义与性质;②平均数定义与性质;③求平均数的基本方法。
【解题思路】根据统计折线图和平均数的性质,运用求平均数的基本方法,结合问题条件分别求出 2012年-2021年工业企业利润总额增速和电子信息制造业企业利润总额增速的均值
,对各选项的正确与错误进行判断就可得出选项。
【详细解答】从统计折线图可以看出,电子信息制造也企业和工业企业都有负的增速, 2012年-2021年电子信息制造业企业和工业企业利润总额都不是逐年递增,A,B错误;从统计折线图可以看出,2012年-2017年电子信息制造业企业利润总额均比上一年实现增长,且其增速快于当年工业企业利润总额增速, C正确; 2012年-2021年工业企业利润总额增速的均值为=9.34(%),2012年-2021年电子制造业企业利润总额增速的均值为
=14.24(%),9.34%<14.24%,
2012年-2021年工业企业利润总额增速的均值小于递增信息制造业企业利润总额增速均
值,D错误,C正确,选C。
4、一次数学考试后,某班级平均分为110分,方差为,现发现有两名同学的成绩计算有误,甲同学成绩被误判为113分,实际得分为118分,乙同学成绩被误判为120分,实际成绩为115分,更正后重新计算,得到方差为,则与的大小关系为( )(成都市高2020级高三三珍)
A = B > C < D 不能确定
【解析】
【考点】①平均数定义与性质;②方差定义与性质;③求一组数据平均数的基本方法;④求一组数据方差的基本方法。
【解题思路】根据平均数和方差的性质,运用求一组数列平均数和方差的基本方法,分别求出误判和实际数据的平均数和方差,从而得到与的大小关系就可得出选项。
【详细解答】误判时甲同学比实际少计了5分,乙同学比实际多计了5分,误判和实际的平均法不变,甲同学误判分与实际分和平均分的差的平方分别为9和64,,乙同学误判分与实际分和平均分的差的平方分别为100和25,9+100=109,64+25=89,109-89=20>0, > ,B正确,选B。
5、(理)若数据9,m,6,n,5的平均数为7,方差为2,则数据11,9,2m-1,17,2n-1的平均数和方差分别为( )
A 13,4 B 14,4 C 13,8 D 14,8
(文)若数据9,m,6,5的平均数为7,则数据17, 2m-1,11,9的平均数和方差分别为( )(成都市2020级高三零诊)
A 13,5 B 14,5 C 13,10 D 14,10
【解析】
【考点】①数据平均数定义与性质;②数据方差定义与性质;③求一组数据平均数的基本方法;④求一组数据方差的基本方法。
【解题思路】(理)根据数据平均数和方差的性质,运用求一组数据平均数和方程的基本方法,结合问题条件得到关于m,n的方程组,求解方程组求出m,n的值,从而求出数据11,9,2m-1,17,2n-1的平均数和方差,就可得出选项。(文)根据数据平均数和方差的性质,运用求一组数据平均数和方程的基本方法,结合问题条件得到关于m的方程,求解方程求出m的值,从而求出数据17, 2m-1,11,9的平均数和方差,就可得出选项。
【详细解答】(理)数据9,m,6,n,5的平均数为7,方差为2, m+n=35-(9+6+5)=15①,+ =10-(4+1+4)=1②,联立①②解得:m=8,n=7,11,9,2m-1,17,
2n-1为11,9,15,17,13,数据11,9,15,17,13的平均数为=13,
方差为=8,C正确,选C。
(文)数据9,m,6,5的平均数为7, m=28-(9+6+5)=8, 数据17,2m-1,11,9为数据17,15,11,9, 数据17,15,11,9的平均数为=13,方差为3、6、某地区通过公益讲座以及普及社区居民的垃圾分类知识,为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如下图:则( )(2022全国高考甲卷)
A讲座前问卷答题的正确率的中位数小于70%
B讲座后问卷答题的正确率的平均数大于85%
C讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D 讲座后问卷答题的正确率的极差大于讲座前正确率的极差
【解析】
【考点】①随机变量散点图定义与性质;②中位数定义与基本求法;③平均数定义与基本求法;④标准差定义与基本求法;⑤极差定义与基本求法。
【解题思路】根据随机变量散点图的性质,运用求中位数,平均数,标准差和极差的基本方法,结合问题条件分别求出讲座前问卷答题的正确率的中位数,讲座后问卷答题的正确率的平均数,讲座前问卷答题的正确率的标准差与讲座后正确率的标准差,讲座后问卷答题的正确率的极差与讲座前正确率的极差,就可得出选项。
【详细解答】讲座前问卷答题的正确率的中位数为=72.5%>70%,A错误;讲座后问卷答题的正确率的平均数为= =89.5
%>85%, B正确,选B。
7、四名同学各掷骰子5次,并各自记录每次骰子出现的点数,分别统计四名同学的纪录结果,可以判断出一定没有出现点数6的是( )(成都市2019级高三一诊)
A 平均数为3,中位数为2 B 中位数为3,众数为2
C 中位数为3,方差为2.8 D 平均数为2,方差为2.4
【解析】
【考点】①平均数定义与性质;②中位数定义与性质;③众数定义与性质;④方差定义与性质。
【解题思路】根据平均数,中位数,众数和方差的性质,运用求平均数,中位数,众数和方差的基本方法,对各选项进行判断就可得出选项。
【详细解答】设表示某名同学纪录自记每次骰子出现的点数由小到大排列时第i(i=1,2,3,4,5)次骰子出现的点数,对A,平均数为3,中位数为2, 这名同学的纪录结果中 ,骰子出现点数之和为35=15,=1或2,=1 或2,=2,++2+2+26, +15-69,当=3时,必有=6, A错误;对B,中位数为3,众数为2,==2,=3,++=2+2+3=7,,中有可能其中一个(或两个)是6,
B错误;对C,中位数为3,方差为2.8,=1或2或3,=1 或2或3,=3,当==1,=3时,,两个点数大于或等于3,平均数大于2,若平均数为3,+=35-5
=10,当=4时,=6, C错误;对D, 平均数为2,方差为2.4, =2.420=48,若,,,,有1次骰子出现的点数为6,不妨设=6,==16,方差3.2>2.4,,,,,中不可能有6D正确,选D。
8、有一组样本数据,,------,,由这组数据得到新样本数据,,-------,,其中=+c(i=1,2,-----,n),c为非零常数,则( )(2021全国高考新高考I)
A 两组样本数据的样本平均数相同 B 两组样本数据的样本中位数相同
C 两组样本数据的样本标准差相同 D 两组样本数据的样本极差相同
【解析】
【考点】①样本定义与性质;②样本平均数定义与性质;③样本中位数定义与性质;④样本
标准差定义与性质;⑤样本极差定义与性质;⑥求一组数据平均数,中位数,标准差和极差的基本方法。
【解题思路】根据样本,样本平均数,样本中位数,样本标准差和样本极差的性质,运用求一组数据平均数,中位数,标准差和极差的基本方法,结合问题条件分别求出两个样本数据的平均数,中位数,标准差和极差就可得出选项。
【详细解答】样本数据,,------,的平均数= ,新样本数据,,-------,的平均数= =+c,,A错误;样本数据,,------,的中位数与新样本数据,,-------,的中位数=+c,+c,B错误;样本数据,,------,的标准差=,新样本数据,,-------,的标准差==
==,C正确;样本数据,,------,的极差=-,新样本数据,,-------,的极=-=+c--c=-,D正确,C,D正确,选C,D。
『思考问题3』
(1)【典例3】是统计指标及运用的问题,解答这类问题需要理解平均数,方差,标准差的定义,掌握求平均数,方差,标准差的基本求法;
(2)总体估计的常用方法有:①点估计;②区间估计;
(3)点估计是直接运用样本指标作为总体指标,常用的样本指标有:①样本的平均数;②样本的标准差;③样本的方差;常用的总体指标有:①总体的平均数;②总体的标准差;③总体的方差;
(4)区间估计是根据问题要求可靠程度去确定总体指标取值的区间,其基本方法是:①由问题要求的可靠程度确定抽样的平均误差;②根据抽样平均误差确定抽样误差的允许范围;③根据抽样误差的允许范围确定总体指标的取值范围。
[练习3]解答下列问题:
1、下列统计量中,能度量样本,,------,的离散程度的是( )(2021全国高考新高考I)(答案:A,C)
A 样本,,------,的标准差 B 样本,,------,的中位数
C 样本,,------,的极差 D 样本,,------,的平均数
2、甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是:,分别表示甲乙两组数据的平均数,,分别表示甲乙两组数据的方差,则下列选项正确的
甲 0 1 0 2 2 0 3 1 2 4
乙 2 2 1 1 1 2 1 1 0 1
是( )(成都市2021高三一诊)(答案:B)
A = ,> B >,> C <,< D >,<
3、某市环境保护局公布了该市A,B两个景区2014年至2020年各年的全年空气质量优良天数的数据,现根据这些数据绘制了如图所示的折线图,则由该折线图得出的下列结论中正确的是( )(成都市2021高三三诊)(答案:D)
A 景区A这7年的空气质量优良天数的极差为98 B 景区B这7年的空气质量优良天数的中位数为283 C 分别记景区A,B这7年的空气质量优良天数的众数为,,则>
D分别记景区A,B这7年的空气质量优良天数的标准差为 ,,则 >
4、(理)在一组样本数据中,1,2,3,4出现的频率分别为,,,,且=1,
则下列四种情形中,对应样本的标准差最大的一组是( )(答案:B)
A ==0.1,==0.4 B ==0.4,==0.1
C ==0.2,==0.3 D ==0.3,==0.2
(文)设一组样本数据,,-------,的方差为0.01,则数据10,10,-------,10的方差为( )(2020全国高考新课标III)(答案:C)
A 0.01 B 0.1 C 1 D 10
【典例4】解答下列问题:
1、 对变量x,y有观测数据(,)(i),得散点图1;对变量u,v有观测数据(,
)(i)得散点图2,表示变量x,y之间的线性相关系数,表示变量u,v之间的线性相关系数,则下列说法正确的是( )(成都市高2021级高三二诊)
A 变量x,y呈正相关,且||<|| B 变量x,y呈负相关,且||>||
C 变量x,y呈正相关,且||>|| D 变量x,y呈负相关,且||<||
【解析】
【考点】①随机变量散点图定义与性质;②随机变量相关系数定义与性质;③随机变量正相关定义与性质;④随机变量负相关定义与性质。
【解题思路】根据随机变量散点图,相关系数,正相关和负相关的性质,结合问题条件对各选项说法的正确性进行判断就可得出选项。
【详细解答】根据随机变量x,y 的散点图可知,随机变量x,y呈正相关, B,D错误;根据随机变量散点图可知,随机变量x,y比随机变量u,v的线性相关更大, ||>||,
A错误,C正确,选C。
2、如图,由观察数据(,)(i=1,2,3,4,5,6)的散点图可知,y与x的关系可以
用模型y=blnx+a拟合,设z=lnx,利用最小二乘法求得y关于z的回归方程=z+1,已知=,=18,则=( )(成都市高2021级高三三诊)
A B C 1 D
【解析】
【考点】①变量散点图及运用;②函数模型定义与性质;③线性回归方程定义与性质;④求线性回归方程的基本方法。
【解题思路】根据函数模型和线性回归方程的性质,运用变量散点图和求线性回归方程的基本方法,结合问题条件求出的值就可得出选项。
【详细解答】=,z=lnx,=18,=z+1,===3,
=====2,1=-,
===1,C正确,选C。
3、下列命题中错误的是( )(成都市高2020级高三一诊)
A 在回归分析中,相关系数r的绝对值越大,两个变量的线性相关性越强 B 对分类变量X与Y,它们的随机变量的观测值k越小,说明“X与Y有关系”的把握性越大 C 线性回归直线=x+恒过点(,) D 在回归分析中,残差平方越小,模型的拟合效果越好
【解析】
【考点】①相关系数定义与性质;②判断两个随机变量线性相关的基本方法;③独立性检验定义与性质;④求线性回归方程的基本方法。
【解题思路】根据相关系数和独立性检验的性质,运用判断两个随机线性相关和求线性回归方程的基本方法,对各命题的真假进行判断就可得出选项。
【详细解答】对A,相关系数r的绝对值越大,两个变量的线性相关性越强,A正确,对B,对分类变量X与Y,它们的随机变量的观测值k越大,说明“X与Y有关系”的把握性越大,B错误;对C,=-,当x=时,=+-=, 线性回归直线=x+恒过点(,),C正确;对D, 在回归分析中,残差平方越小,模型的拟合效果越好,D正确, B错误,选B。
『思考问题4』
(2)【典例4】是判断两个随机变量相关关系和线性回归方程及运用的问题,解答这类问题需要理解两个随机变量相关和线性回归方程的定义,掌握判断两个随机变量是否具有相关关系和建立线性回归方程及回归分析的基本方法;
(2)判断两个随机变量是否相关的基本方法是:①根据数据作出随机变量的散点图,由散点图进行判断;②运用相关系数的计算公式,通过运算求出相关系数的值,根据相关系数值的大小进行判断;
(3)散点图法的基本方法是:①根据两个变量的一组对应值作出散点 图,②运用散点图判断两个随机变量是否具有相关关系;
(4)相关系数法的基本方法是:①根据两个变量的一组对应值运用公式计算相关系数的值,
②根据计算结果判断两个随机变量是否具有相关关系;
(7)判断两个变量是正相关还是负相关的常用方法是:①散点图法,②相关系数法,③运用线性回归方程=x+中的系数,若 > 0,为正相关;若 < 0为负相关。
(6)建立线性回归方程的基本方法是:①判断两个变量是否具有线性相关关系,②运用公式:
=, =- 求出回归系数,(也可以用待定系数法,即根据回归直线过样本点的中心求系数,),③写出回归直线方程;
(8)回归分析及回归预测的基本方法是:①依据回归直线方程视为变量y是变量x(或t)的一次函数,②将变量x(或t)的值代入回归直线方程求出变量y的值;③得出统计预测结果。
[练习4]解答下列问题:
1、某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:)的关系,在20个不同温度条件下进行种子发芽率实验,由实验数据(,)(i=1,2------,20)得到如下散点图:由此散点图,在10至40之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型是( )(2020全国高考新课标I)(答案:D)
A y=a+bx B y=a+b C y=a+b D y=a+blnx
2、某实验室对小白鼠体内x,y两项指标进行 小白鼠体内x 120 110 125 130 115
研究,连续五次实验所测得的这两项指标数据如 小白鼠体内y 92 83 90 96 89
表所示,已知y与x具有线性相关关系,利用表中数据求得回归直线方程为=x+,若下一次实验中x=170,利用该回归直线方程预测得=117,则的值为 (成都市2020
高三三诊)(答案:=0.54。)
【典例5】解答下列问题:
1、在某大学一食品超市,随机询问了70名不同性别 女 男 总计
的大学生在购买食物时是否查看营养说明,得到如下 要查看营养说明 15 25 40
的列联表:(成都市2019级高三三珍) 不查看营养说明 20 10 30
附:=其中n=a+b+c+d。 总计 35 35 70
P() 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005
0.455 0.708 1.323 2.702 2.706 3.841 5.024 6.635 7.879
根据列联表的独立性检验,则下列说法正确的是( )
A 在犯错误的概率不超过0.05的前提下,认为该校大学生在购买食物时要查看营养说明的人数中男生人数更多 B在犯错误的概率不超过0.010的前提下,认为该校大学生在购买食物时要查看营养说明的人数与不查看营养说明的人数比是 C 在犯错误的概率不超过0.025的前提下,认为性别与是否查看营养说明有关 D 在犯错误的概率不超过0.010的前提下,认为性别与是否查看营养说明有关
【解析】
【考点】①分类变量定义与性质;②列联表定义与性质;③独立性检验定义与性质;④随机变量计算公式及运用;⑤判断两个分类变量是否相关的基本方法。
【解题思路】根据分类变量,列联表和独立性检验的性质,运用计算随机变量的公式,结合问题条件求出随机变量的值,利用判断两个分类变量是否相关的基本方法,对该校大学生购买食物时,性别与是否查看营养说明的相关关系进行判断就可得出选项。
【详细解答】===5.833,5.024<5.833<6.635在犯错误的概率不超过0.025的前提下,认为性别与是否查看营养说明有关, C正确,选C。
『思考问题5』
(1)【典例5】是独立性检验的问题,解答这类问题需要理解分类变量,独立性检验的定义,了解2x2列联表的意义,掌握独立性检验的基本方法;
(2)比较两个分类变量是否有关的基本方法是:①计算的值进行判断,越大两个分类变量有关的可能性越大;②计算|ad-bc|的值进行判断,|ad-bc|越大两个分类变量有关的可能性越大;
(3)独立性检验的基本方法是:①根据样本数据制成2x2列联表,②运用公式=
计算的观察值,③比较与临界值的大小,作出推断。
【典例6】解答下列问题:
1、为了解推动出口后某收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后某收入的样本均值=2。1,样本方差=0.01,已知该种植区以往的某收入服从正态分布N(1.8,),假设推动出口后的某收入Y服从正态分布N(,),则( )(2024全国高考新高考I)(若随机变量Z服从正态分布N(u,),则p(Z<u+)0.8413)
A p(X>2)>0.2 B p(X>2)<0.5 C p(X>2)>0.5 D p(X>2)<0.8
【解析】
【考点】①随机变量正态分布定义与性质;②随机变量正态分布图像及运用。
【解题思路】根据随机变量正态分布的性质,运用随机变量正态分布的图像,结合问题条件求出p(X>2)的值就可得出选项。
【详细解答】该种植区以往的某收入服从正态分布N(1.8,),u=1.8,=0,1, p(Z<u+)0.8413, p(Z>u+)=1- p(Z<u+)1-0.84130.1587,p(X>2)= p(Z>u+2)<p(Z>u+)0.1587,B正确;推动出口后的某收入Y服从正态分布N(2.1,0。01),u=2.1,=0,1, p(Z<u+)0.8413, p(X>2)= p(Z>u-)= p(Z<u+)0.8413,C正确,综上所述,B,C正确,选B,C。
2、随机变量X服从正态分布N(2,),若p(2
【解析】
【考点】①随机变量正态分布定义与性质;②随机变量正态分布图像及运用。
【解题思路】根据随机变量正态分布的性质,运用随机变量正态分布的图像,结合问题条件就可求出p(X>2.5)的值。
【详细解答】随机变量X服从正态分布N(2,),p(2
(1)【典例6】是与正太分布相关的问题,解答这类问题需要理解正太曲线,正太分布的定义,了解正太曲线的性质,掌握正太分布下概率计算的基本方法;
(2)正太曲线的主要性质是:①曲线在x轴的上方,且与x轴不相交;②正态曲线的图像关于直线x=u对称;③曲线在x=u时达到高峰值,由这一点向左,右两边延伸时,曲线逐渐降低;
(3)正太变量在(-∞,+∞)内取值的概率是1,对于固定的u,来说,随机变量在(u-,u+)上的取值的概率随着的减小而增大,即越小,随机变量X取值落在(u-,u+)的概率越大。
[练习6]解答下列问题:
1、某物理量的测量结果服从正太分布N(10,),下列结论中不正确的是( )(2021全国高考新高考II)(答案:D)
A 越小,该物理量在一次测量中在(9.9,10.1)的概率越大 B 越小,该物理量在一次测量中大于10的概率为0.5 C 越小,该物理量在一次测量中小于9.99与大于10.01的概率相等 D 越小,该物理量在一次测量中落在(9.9,10.2)与落在(10,10.3)的概率相等
同课章节目录
