11.3多边形及其内角和+同步分层训练(基础卷)(含解析)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 11.3多边形及其内角和+同步分层训练(基础卷)(含解析)2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 79.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 16:11:17 | ||
图片预览




文档简介
人教版八年级数学上册 11.3多边形及其内角和 同步分层训练(基础卷)
班级: 姓名:
一、选择题
1.若从边形的一个顶点出发,可以画出条对角线,则的值是( )
A. B. C. D.
2.五边形的对角线共有( )
A.3条 B.4条 C.5条 D.6条
3.若一个多边形从一个顶点所作的对角线为5条,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.五边形的对角线的总条数是( )
A.3 B.4 C.5 D.6
5.如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成5个三角形,那么从这个多边形的一个顶点出发对角线有( )条
A.2 B.3 C.4 D.5
6.五边形的外角和为( )
A.360° B.540° C.720° D.900°
7.若n边形的内角和比它的外角和的3倍少,则n是( )
A.5 B.7 C.8 D.9
8.如果一个多边形的每一个内角都是144°,则这个多边形的边数是( )
A.十 B.九 C.八 D.七
9.如果一个多边形的每一个外角都是45°,那么这个多边形的内角和是( )
A.540° B.720° C.1080° D.1260°
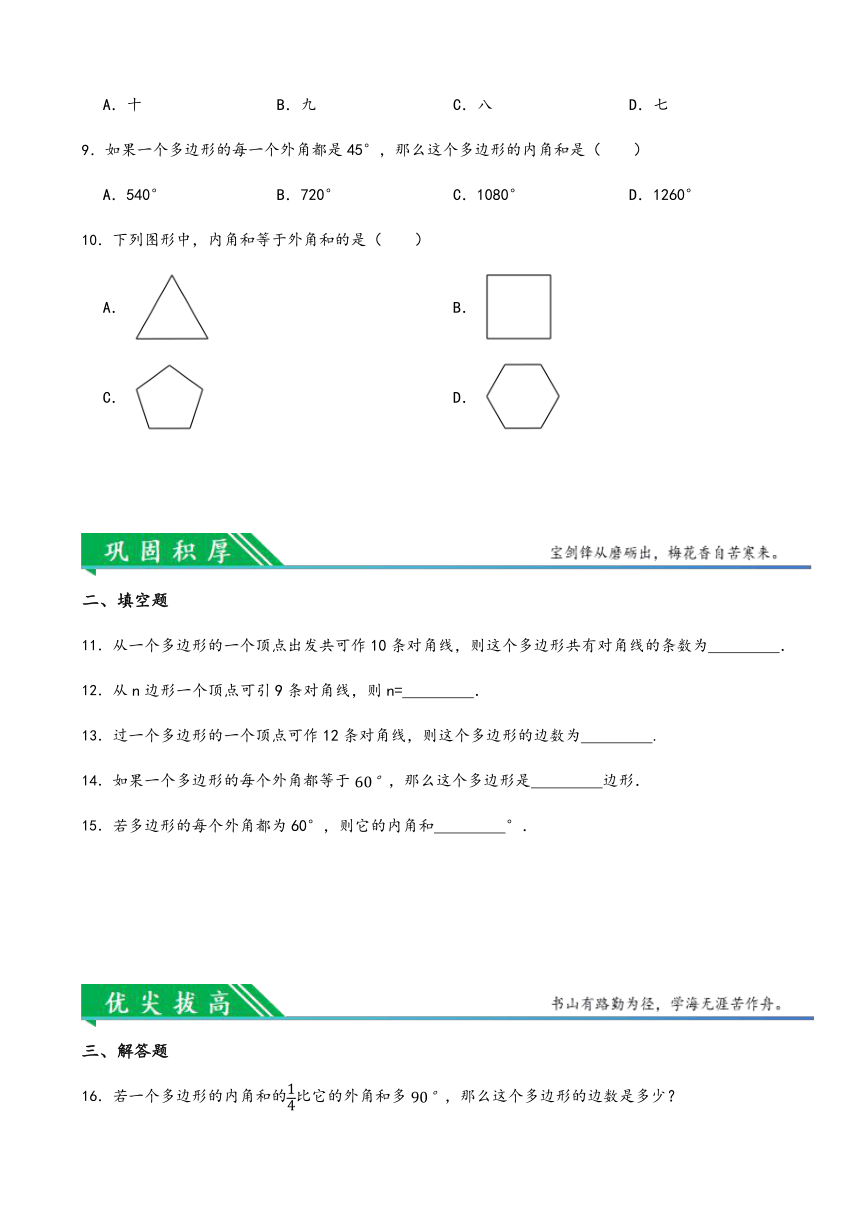
10.下列图形中,内角和等于外角和的是( )
A. B.
C. D.
二、填空题
11.从一个多边形的一个顶点出发共可作10条对角线,则这个多边形共有对角线的条数为 .
12.从n边形一个顶点可引9条对角线,则n= .
13.过一个多边形的一个顶点可作12条对角线,则这个多边形的边数为 .
14.如果一个多边形的每个外角都等于,那么这个多边形是 边形.
15.若多边形的每个外角都为60°,则它的内角和 °.
三、解答题
16.若一个多边形的内角和的比它的外角和多,那么这个多边形的边数是多少?
17.如图,在五边形ABCDE中满足 AB∥CD,求图形中的x的值.
已知多边形的边数恰好是从这个多边形的一个顶点出发的对角线条数的2倍,求此多边形的边数.
已知多边形的边数恰好是从这个多边形的一个顶点出发的对角线条数的2倍,求此多边形的内角和.
四、综合题
20.已知一个n边形的每一个内角都等于150°.
(1)求n.
(2)求这个n边形的内角和.
21.一个多边形的内角和是外角和的3倍.
(1)求这个多边形的边数;
(2)这个多边形一共有多少条对角线?
22.已知一个多边形的内角和与外角和的差为1080°.
(1)求这个多边形的边数.
(2)求此多边形的对角线条数.
23.如图,在四边形中,,分别是及的平分线.
(1)求证:;
(2)若,求.
1.【答案】D
【解析】【解答】解:设多边形有 条边,
则 ,
解得 ,
故答案为:D.
【分析】设多边形有 条边,根据题意列出方程,再求出n的值即可。
2.【答案】C
【解析】【解答】解:五边形的对角线共有 条,
故答案为:C.
【分析】根据多边形对角线总条数的计算公式 进行计算即可.
3.【答案】D
【解析】【解答】设多边形是n边形,由对角线公式,得:
.
解得n=8,
∴这个多边形是八边形,
故答案为:D.
【分析】根据n边形对角线公式,即可求得答案.
4.【答案】C
【解析】【解答】解:五边形的一个顶点处有5-3=2条对角线,共有 条对角线.
故答案为:C.
【分析】根据多边形的对角线的规律,n边形的一个顶点处有(n-3)条对角线,总共有 条对角线,据此解答即可.
5.【答案】C
【解析】【解答】解:设多边形有n条边,
则n 2=5,
解得:n=7.
所以这个多边形的边数是7,
从这个多边形的一个顶点出发对角线有7 3=4条对角线.
故答案为:B.
【分析】经过n边形的一个顶点的所有对角线把多边形分成(n-2)个三角形,根据此关系式求边数,再求出从这个多边形的一个顶点出发的对角线条数.
6.【答案】A
【解析】【解答】五边形的外角和是360°.
故答案为:A.
【分析】利用多边形的外角和求解即可。
7.【答案】B
【解析】【解答】解:设这个多边形的边数为n,则内角和为,依题意得:
,解得.
故答案为:B
【分析】设这个多边形的边数为n,则内角和为,根据“ n边形的内角和比它的外角和的3倍少 ”列出方程并解之即可.
8.【答案】A
【解析】【解答】解: ∵一个多边形的每一个内角都是144° ,
∴该多边形的每一个外角为180°-144°=36°,
∴该多边形的边数为360°÷36°=10.
故答案为:A.
【分析】根据多边形的每一个外角与之相邻的内角互补可求出该多边形的一个外角的度数,进而用外角和360°除以一个外角的度数即可求出该多边形的边数.
9.【答案】C
【解析】【解答】解:多边形的边数为:360°÷45°=8,
多边形的内角和是:(8﹣2) 180°=1080°.
故答案为:C.
【分析】利用外角和360°除以外角的度数可得多边形的边数,然后根据内角和公式(n-2)×180°进行计算.
10.【答案】B
【解析】【解答】解:设n边形的内角和等于外角和
(n-2)×180°=360°
解得:n=4
故答案为:B
【分析】设n边形的内角和等于外角和,根据题意列出方程(n-2)×180°=360°求解即可。
11.【答案】65
【解析】【解答】解:设多边形为n边形,根据题意可知:,
∴,
∴这个多边形共有对角线的数量为:,
故答案为:65.
【分析】先求出多边形的边数,再利用多边形对角线的数量与边数的关系可得答案。
12.【答案】12
【解析】【解答】解:设多边形有n条边,
则n-3=9,解得n=12,
故答案为12.
【分析】设多边形有n条边,再根据多边形的对角线的条数与边数的关系求解可得n-3=9,即可求出边数n。
13.【答案】15
【解析】【解答】解:∵多边形从每一个顶点出发都有12条对角线,
∴多边形的边数为12+3=15,
∴这个多边形是十五边形.
故答案为:15.
【分析】n多边形从每一个顶点出发都有(n-3)条对角线,据此解答即可.
14.【答案】六
【解析】【解答】解:∵多边形的外角和为,每一个外角都等于,
∴多边形的边数为.
故答案为:6.
【分析】利用多边形的外角和除以外角的度数即得边数.
15.【答案】720
【解析】【解答】解:(360°÷60°﹣2)×180°
=(6﹣2)×180
=4×180°
=720°
故答案为:720.
【分析】利用外角和360°除以外角的度数可得多边形的边数,然后根据内角和公式(n-2)×180°进行计算.
16.【答案】解:设这个多边形的边数是n,
由题意得:,
解得:,
答:这个多边形的边数是12.
【解析】【分析】设这个多边形的边数是n,根据题中的相等关系“多边形的内角和×=360°+90°”可列关于n的方程,解方程可求解.
17.【答案】解:∵AB∥CD,∠C=60°,
∴∠B=180°﹣60°=120°,
∴(5﹣2)×180°=x+150°+125°+60°+120°,
∴x=85°.
【解析】【分析】由二直线平行,同旁内角互补可得∠B的度数,然后结合多边形的内角和公式进行计算.
18.【答案】解:设此多边形有n条边,由题意,得
n=2(n-3),
解得n=6.
故此多边形有6条边.
【解析】【分析】根据多边形对角线的规律:从一个点出发可引(n-3)(n大于3)列出方程求解即可。
19.【答案】解:设多边形的边数为n,
则n=2(n-3),
解得n=6,
∴(n-2)×180=4×180=720度.
【解析】【分析】设此多边形有n条边,则从一个顶点引出的对角线有(n-3)条,根据“一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍”列出方程,解方程得出该多边形的边数,进而根据多边形的内角和公式即可出答案.
20.【答案】(1)解:∵每一个内角都等于150°,
∴每一个外角都等于180°-150°=30°,
∴边数n=360°÷30°=12;
(2)解:内角和:12×150°=1800°.
【解析】【分析】(1)首先求出外角度数,再用360°除以外角度数可得答案;(2)利用每一个内角度数150°×内角的个数即可.
21.【答案】(1)解:设这个多边形的边数是n,根据题意得,
(n-2)×180°=3×360°
解得n=8,
答:这个多边形的边数是8
(2)解:过这个多边形的一个顶点可以作对角线共:8-3=5 (条)
【解析】【分析】(1)多边形的内角和为360°,根据多边形的内角和定理求出边数即可;
(2)根据多边形的对角线公式求出答案即可。
22.【答案】(1)解:设这个多边形的边数为,
由题意得,
解得.
答:这个多边形的边数为10.
(2)解:此多边形的对角线条数.
【解析】【分析】(1) 设这个多边形的边数为, 根据多边形的内角和与外角和公式,利用多边形的内角和与外角和的差为1080°的等量关系列出方程求解即可;
(2)根据多边形的对角线条数公式列式计算即可.
23.【答案】(1)证明:∵四边形的内角和是,
∴,
∵分别是及的平分线,
∴,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,,
∴,
∵分别是的平分线,
∴.
【解析】【分析】(1)根据四边形内角和为360°可得∠DAB+∠DCB=180°,根据角平分线的概念可得∠FCB=∠DCB,∠BAE=∠DAB,则∠FCB+∠BAE=(∠DCB+∠DAB)=90°,根据同角的余角相等可得∠FCB=∠AEB,然后根据平行线的判定定理进行证明;
(2)根据四边形内角和为360°可得∠DAB=124°,由角平分线的概念可得∠DAE=∠DAB,据此计算.
班级: 姓名:
一、选择题
1.若从边形的一个顶点出发,可以画出条对角线,则的值是( )
A. B. C. D.
2.五边形的对角线共有( )
A.3条 B.4条 C.5条 D.6条
3.若一个多边形从一个顶点所作的对角线为5条,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.五边形的对角线的总条数是( )
A.3 B.4 C.5 D.6
5.如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成5个三角形,那么从这个多边形的一个顶点出发对角线有( )条
A.2 B.3 C.4 D.5
6.五边形的外角和为( )
A.360° B.540° C.720° D.900°
7.若n边形的内角和比它的外角和的3倍少,则n是( )
A.5 B.7 C.8 D.9
8.如果一个多边形的每一个内角都是144°,则这个多边形的边数是( )
A.十 B.九 C.八 D.七
9.如果一个多边形的每一个外角都是45°,那么这个多边形的内角和是( )
A.540° B.720° C.1080° D.1260°
10.下列图形中,内角和等于外角和的是( )
A. B.
C. D.
二、填空题
11.从一个多边形的一个顶点出发共可作10条对角线,则这个多边形共有对角线的条数为 .
12.从n边形一个顶点可引9条对角线,则n= .
13.过一个多边形的一个顶点可作12条对角线,则这个多边形的边数为 .
14.如果一个多边形的每个外角都等于,那么这个多边形是 边形.
15.若多边形的每个外角都为60°,则它的内角和 °.
三、解答题
16.若一个多边形的内角和的比它的外角和多,那么这个多边形的边数是多少?
17.如图,在五边形ABCDE中满足 AB∥CD,求图形中的x的值.
已知多边形的边数恰好是从这个多边形的一个顶点出发的对角线条数的2倍,求此多边形的边数.
已知多边形的边数恰好是从这个多边形的一个顶点出发的对角线条数的2倍,求此多边形的内角和.
四、综合题
20.已知一个n边形的每一个内角都等于150°.
(1)求n.
(2)求这个n边形的内角和.
21.一个多边形的内角和是外角和的3倍.
(1)求这个多边形的边数;
(2)这个多边形一共有多少条对角线?
22.已知一个多边形的内角和与外角和的差为1080°.
(1)求这个多边形的边数.
(2)求此多边形的对角线条数.
23.如图,在四边形中,,分别是及的平分线.
(1)求证:;
(2)若,求.
1.【答案】D
【解析】【解答】解:设多边形有 条边,
则 ,
解得 ,
故答案为:D.
【分析】设多边形有 条边,根据题意列出方程,再求出n的值即可。
2.【答案】C
【解析】【解答】解:五边形的对角线共有 条,
故答案为:C.
【分析】根据多边形对角线总条数的计算公式 进行计算即可.
3.【答案】D
【解析】【解答】设多边形是n边形,由对角线公式,得:
.
解得n=8,
∴这个多边形是八边形,
故答案为:D.
【分析】根据n边形对角线公式,即可求得答案.
4.【答案】C
【解析】【解答】解:五边形的一个顶点处有5-3=2条对角线,共有 条对角线.
故答案为:C.
【分析】根据多边形的对角线的规律,n边形的一个顶点处有(n-3)条对角线,总共有 条对角线,据此解答即可.
5.【答案】C
【解析】【解答】解:设多边形有n条边,
则n 2=5,
解得:n=7.
所以这个多边形的边数是7,
从这个多边形的一个顶点出发对角线有7 3=4条对角线.
故答案为:B.
【分析】经过n边形的一个顶点的所有对角线把多边形分成(n-2)个三角形,根据此关系式求边数,再求出从这个多边形的一个顶点出发的对角线条数.
6.【答案】A
【解析】【解答】五边形的外角和是360°.
故答案为:A.
【分析】利用多边形的外角和求解即可。
7.【答案】B
【解析】【解答】解:设这个多边形的边数为n,则内角和为,依题意得:
,解得.
故答案为:B
【分析】设这个多边形的边数为n,则内角和为,根据“ n边形的内角和比它的外角和的3倍少 ”列出方程并解之即可.
8.【答案】A
【解析】【解答】解: ∵一个多边形的每一个内角都是144° ,
∴该多边形的每一个外角为180°-144°=36°,
∴该多边形的边数为360°÷36°=10.
故答案为:A.
【分析】根据多边形的每一个外角与之相邻的内角互补可求出该多边形的一个外角的度数,进而用外角和360°除以一个外角的度数即可求出该多边形的边数.
9.【答案】C
【解析】【解答】解:多边形的边数为:360°÷45°=8,
多边形的内角和是:(8﹣2) 180°=1080°.
故答案为:C.
【分析】利用外角和360°除以外角的度数可得多边形的边数,然后根据内角和公式(n-2)×180°进行计算.
10.【答案】B
【解析】【解答】解:设n边形的内角和等于外角和
(n-2)×180°=360°
解得:n=4
故答案为:B
【分析】设n边形的内角和等于外角和,根据题意列出方程(n-2)×180°=360°求解即可。
11.【答案】65
【解析】【解答】解:设多边形为n边形,根据题意可知:,
∴,
∴这个多边形共有对角线的数量为:,
故答案为:65.
【分析】先求出多边形的边数,再利用多边形对角线的数量与边数的关系可得答案。
12.【答案】12
【解析】【解答】解:设多边形有n条边,
则n-3=9,解得n=12,
故答案为12.
【分析】设多边形有n条边,再根据多边形的对角线的条数与边数的关系求解可得n-3=9,即可求出边数n。
13.【答案】15
【解析】【解答】解:∵多边形从每一个顶点出发都有12条对角线,
∴多边形的边数为12+3=15,
∴这个多边形是十五边形.
故答案为:15.
【分析】n多边形从每一个顶点出发都有(n-3)条对角线,据此解答即可.
14.【答案】六
【解析】【解答】解:∵多边形的外角和为,每一个外角都等于,
∴多边形的边数为.
故答案为:6.
【分析】利用多边形的外角和除以外角的度数即得边数.
15.【答案】720
【解析】【解答】解:(360°÷60°﹣2)×180°
=(6﹣2)×180
=4×180°
=720°
故答案为:720.
【分析】利用外角和360°除以外角的度数可得多边形的边数,然后根据内角和公式(n-2)×180°进行计算.
16.【答案】解:设这个多边形的边数是n,
由题意得:,
解得:,
答:这个多边形的边数是12.
【解析】【分析】设这个多边形的边数是n,根据题中的相等关系“多边形的内角和×=360°+90°”可列关于n的方程,解方程可求解.
17.【答案】解:∵AB∥CD,∠C=60°,
∴∠B=180°﹣60°=120°,
∴(5﹣2)×180°=x+150°+125°+60°+120°,
∴x=85°.
【解析】【分析】由二直线平行,同旁内角互补可得∠B的度数,然后结合多边形的内角和公式进行计算.
18.【答案】解:设此多边形有n条边,由题意,得
n=2(n-3),
解得n=6.
故此多边形有6条边.
【解析】【分析】根据多边形对角线的规律:从一个点出发可引(n-3)(n大于3)列出方程求解即可。
19.【答案】解:设多边形的边数为n,
则n=2(n-3),
解得n=6,
∴(n-2)×180=4×180=720度.
【解析】【分析】设此多边形有n条边,则从一个顶点引出的对角线有(n-3)条,根据“一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍”列出方程,解方程得出该多边形的边数,进而根据多边形的内角和公式即可出答案.
20.【答案】(1)解:∵每一个内角都等于150°,
∴每一个外角都等于180°-150°=30°,
∴边数n=360°÷30°=12;
(2)解:内角和:12×150°=1800°.
【解析】【分析】(1)首先求出外角度数,再用360°除以外角度数可得答案;(2)利用每一个内角度数150°×内角的个数即可.
21.【答案】(1)解:设这个多边形的边数是n,根据题意得,
(n-2)×180°=3×360°
解得n=8,
答:这个多边形的边数是8
(2)解:过这个多边形的一个顶点可以作对角线共:8-3=5 (条)
【解析】【分析】(1)多边形的内角和为360°,根据多边形的内角和定理求出边数即可;
(2)根据多边形的对角线公式求出答案即可。
22.【答案】(1)解:设这个多边形的边数为,
由题意得,
解得.
答:这个多边形的边数为10.
(2)解:此多边形的对角线条数.
【解析】【分析】(1) 设这个多边形的边数为, 根据多边形的内角和与外角和公式,利用多边形的内角和与外角和的差为1080°的等量关系列出方程求解即可;
(2)根据多边形的对角线条数公式列式计算即可.
23.【答案】(1)证明:∵四边形的内角和是,
∴,
∵分别是及的平分线,
∴,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,,
∴,
∵分别是的平分线,
∴.
【解析】【分析】(1)根据四边形内角和为360°可得∠DAB+∠DCB=180°,根据角平分线的概念可得∠FCB=∠DCB,∠BAE=∠DAB,则∠FCB+∠BAE=(∠DCB+∠DAB)=90°,根据同角的余角相等可得∠FCB=∠AEB,然后根据平行线的判定定理进行证明;
(2)根据四边形内角和为360°可得∠DAB=124°,由角平分线的概念可得∠DAE=∠DAB,据此计算.
