第二十二章二次函数单元练习(无答案)2024—2025学年人教版数学九年级上册
文档属性
| 名称 | 第二十二章二次函数单元练习(无答案)2024—2025学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 277.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 16:12:12 | ||
图片预览

文档简介
第二十二章 二次函数 单元练习
2024-2025学年人教版数学九年级上册
一、单选题
1.下列y关于x的函数中,一定是二次函数的是( )
A. B. C. D.
2.将二次函数化为的形式,正确的结果是( )
A. B.
C. D.
3.如图.抛物线经过点,对称轴为直线,则当时,的取值范围是( )
A. B.或
C.或 D.
4.如图,是二次函数的图象,若关于的方程总有一正一负两个实数根,则的取值范围是( )
A. B. C. D.
5.新定义:与被称为“同族二次函数”,若和是同族二次函数,则二次函数的开口方向和最值为( )
A.开口向上,最小值为2018 B.开口向下,最大值为2018
C.开口向上,最小值为2019 D.开口向下,最大值为2019
6.对于抛物线,下列结论:①抛物线的开口向下;②对称轴为直线;③顶点坐标是;④时,随的增大而减小.其中正确结论的个数为( )
A. B. C. D.
7.如图,人民医院在某流感高发时段,用防护隔帘布临时搭建了一隔离区,隔离区一面靠长为的墙,隔离区分成两个区域,中间也用防护隔帘布隔开.已知整个隔离区所用防护隔帘布总长为,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长,小明认为:隔离区的最大面积为;小亮认为:隔离区的面积可能为,你认为他们俩的说法是( )
A.小明正确,小亮错误 B.小明错误,小亮正确
C.两人均正确 D.两人均错误
8.将抛物线先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的函数表达式为( )
A. B.
C. D.
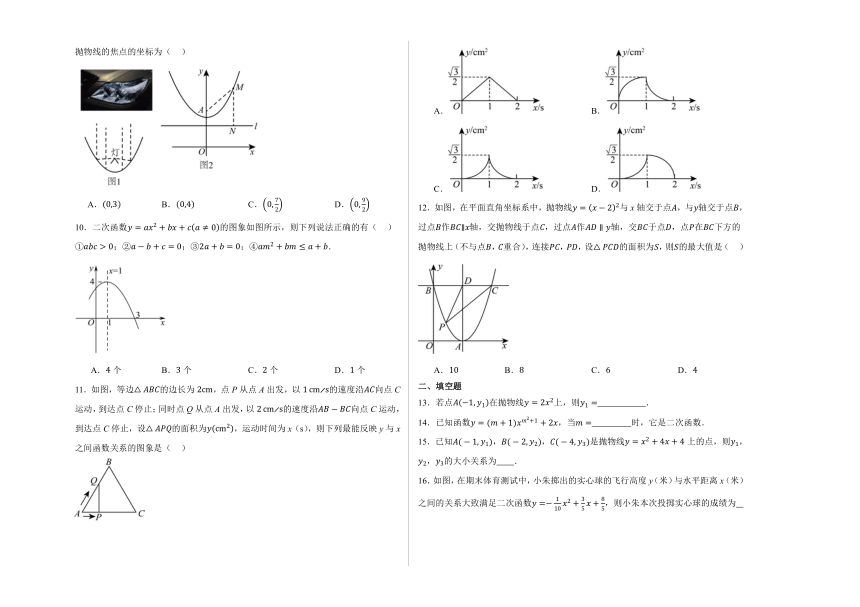
9.如图1,车前大灯反射镜与轴截面的交线是抛物线的一部分,灯所在的位置合适时,灯光会沿着水平方向的反射出去,此时我们称灯的位置为抛物线的“焦点”.抛物线的焦点位置有一种特性:如图,抛物线上任意一点到焦点的距离的长,等于点到一条平行于轴的直线的距离的长.若抛物线的表达式为:,那么此抛物线的焦点的坐标为( )
A. B. C. D.
10.二次函数的图象如图所示,则下列说法正确的有( )
①;②;③;④.
A.个 B.个 C.个 D.个
11.如图,等边的边长为,点P从点A出发,以的速度沿向点C运动,到达点C停止;同时点Q从点A出发,以的速度沿向点C运动,到达点C停止,设的面积为,运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A. B.
C. D.
12.如图,在平面直角坐标系中,抛物线与x轴交于点,与轴交于点,过点作轴,交抛物线于点,过点作轴,交于点,点在下方的抛物线上(不与点,重合),连接,,设的面积为,则的最大值是( )
A. B. C. D.
二、填空题
13.若点在抛物线上,则 .
14.已知函数,当 时,它是二次函数.
15.已知,,是抛物线上的点,则,,的大小关系为 .
16.如图,在期末体育测试中,小朱掷出的实心球的飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数,则小朱本次投掷实心球的成绩为
17.某商品的进价为每件50元,售价为每件60元,每个月可卖出200件.如果每件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于72元),设每件商品的售价上涨x元(x为整数),每个月的销售利润为y元,那么y与x的函数关系式是 .
18.如图,抛物线交轴于,两点;将绕点旋转得到抛物线,交轴于;将绕点旋转得到抛物线,交轴于,,如此进行下去,则抛物线的解析式是
三、解答题
19.如图,有一个竖直的喷水枪AB,由喷水口A喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪AB所在直线的距离为3m,且到地面BC的距离为5m,水流的落地点C到喷水枪底部B的距离为8m,求喷水枪AB的长度.
20.已知抛物线向右平移个单位长度后得到抛物线.
(1)求、的值;
(2)写出抛物线的对称轴及顶点坐标.
21.某网店销售某种儿童玩具,如果每件利润为30元,每天可售出40件.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每天可多销售2件.设销售单价降价x元,每天售出y件.
(1)请写出y与x之间的函数表达式;
(2)当销售单价降低多少元时,该网店每天销售这种玩具获得的利润最大,最大利润是多少?
22.总公司将一批衬衫由甲、乙两家分店共同销售,因地段不同,甲店一天可售出30件,每件盈利30元;乙店一天可售出40件,每件盈利20元.经调查发现,每件衬衫每降价1元,甲、乙两家店一天分别可多售出2,4件.设甲店每件衬衫降价m元时,一天可盈利元,乙店每件衬衫降价n元时,一天可盈利元.
(1)当时,求的值.
(2)求关于n的函数表达式.
(3)若总公司规定:(为正整数),请求出每件衬衫下降多少元时,两家分店一天的盈利和最大,最大是多少元?
23.已知二次函数图象的顶点坐标为,且图象经过点,.
(1)求二次函数的表达式
(2)将二次函数的图象向右平移个单位,图象经过点,求m 的值;
(3)在由(2)平移后的图象上,当时,函数的最小值为,求n的值.
24.如图,抛物线与轴交于,两点.点C为抛物线与轴交点.点为抛物线上任意一点,其横坐标为,过点作轴,点的横坐标为.
(1)求,的值;
(2)当点在抛物线上时,求的值;
(3)当线段与抛物线有两个公共点时,直接写出的取值范围.
2024-2025学年人教版数学九年级上册
一、单选题
1.下列y关于x的函数中,一定是二次函数的是( )
A. B. C. D.
2.将二次函数化为的形式,正确的结果是( )
A. B.
C. D.
3.如图.抛物线经过点,对称轴为直线,则当时,的取值范围是( )
A. B.或
C.或 D.
4.如图,是二次函数的图象,若关于的方程总有一正一负两个实数根,则的取值范围是( )
A. B. C. D.
5.新定义:与被称为“同族二次函数”,若和是同族二次函数,则二次函数的开口方向和最值为( )
A.开口向上,最小值为2018 B.开口向下,最大值为2018
C.开口向上,最小值为2019 D.开口向下,最大值为2019
6.对于抛物线,下列结论:①抛物线的开口向下;②对称轴为直线;③顶点坐标是;④时,随的增大而减小.其中正确结论的个数为( )
A. B. C. D.
7.如图,人民医院在某流感高发时段,用防护隔帘布临时搭建了一隔离区,隔离区一面靠长为的墙,隔离区分成两个区域,中间也用防护隔帘布隔开.已知整个隔离区所用防护隔帘布总长为,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长,小明认为:隔离区的最大面积为;小亮认为:隔离区的面积可能为,你认为他们俩的说法是( )
A.小明正确,小亮错误 B.小明错误,小亮正确
C.两人均正确 D.两人均错误
8.将抛物线先向右平移1个单位长度,再向上平移2个单位长度,得到的抛物线的函数表达式为( )
A. B.
C. D.
9.如图1,车前大灯反射镜与轴截面的交线是抛物线的一部分,灯所在的位置合适时,灯光会沿着水平方向的反射出去,此时我们称灯的位置为抛物线的“焦点”.抛物线的焦点位置有一种特性:如图,抛物线上任意一点到焦点的距离的长,等于点到一条平行于轴的直线的距离的长.若抛物线的表达式为:,那么此抛物线的焦点的坐标为( )
A. B. C. D.
10.二次函数的图象如图所示,则下列说法正确的有( )
①;②;③;④.
A.个 B.个 C.个 D.个
11.如图,等边的边长为,点P从点A出发,以的速度沿向点C运动,到达点C停止;同时点Q从点A出发,以的速度沿向点C运动,到达点C停止,设的面积为,运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A. B.
C. D.
12.如图,在平面直角坐标系中,抛物线与x轴交于点,与轴交于点,过点作轴,交抛物线于点,过点作轴,交于点,点在下方的抛物线上(不与点,重合),连接,,设的面积为,则的最大值是( )
A. B. C. D.
二、填空题
13.若点在抛物线上,则 .
14.已知函数,当 时,它是二次函数.
15.已知,,是抛物线上的点,则,,的大小关系为 .
16.如图,在期末体育测试中,小朱掷出的实心球的飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数,则小朱本次投掷实心球的成绩为
17.某商品的进价为每件50元,售价为每件60元,每个月可卖出200件.如果每件商品的售价上涨1元,则每个月少卖10件(每件售价不能高于72元),设每件商品的售价上涨x元(x为整数),每个月的销售利润为y元,那么y与x的函数关系式是 .
18.如图,抛物线交轴于,两点;将绕点旋转得到抛物线,交轴于;将绕点旋转得到抛物线,交轴于,,如此进行下去,则抛物线的解析式是
三、解答题
19.如图,有一个竖直的喷水枪AB,由喷水口A喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪AB所在直线的距离为3m,且到地面BC的距离为5m,水流的落地点C到喷水枪底部B的距离为8m,求喷水枪AB的长度.
20.已知抛物线向右平移个单位长度后得到抛物线.
(1)求、的值;
(2)写出抛物线的对称轴及顶点坐标.
21.某网店销售某种儿童玩具,如果每件利润为30元,每天可售出40件.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每天可多销售2件.设销售单价降价x元,每天售出y件.
(1)请写出y与x之间的函数表达式;
(2)当销售单价降低多少元时,该网店每天销售这种玩具获得的利润最大,最大利润是多少?
22.总公司将一批衬衫由甲、乙两家分店共同销售,因地段不同,甲店一天可售出30件,每件盈利30元;乙店一天可售出40件,每件盈利20元.经调查发现,每件衬衫每降价1元,甲、乙两家店一天分别可多售出2,4件.设甲店每件衬衫降价m元时,一天可盈利元,乙店每件衬衫降价n元时,一天可盈利元.
(1)当时,求的值.
(2)求关于n的函数表达式.
(3)若总公司规定:(为正整数),请求出每件衬衫下降多少元时,两家分店一天的盈利和最大,最大是多少元?
23.已知二次函数图象的顶点坐标为,且图象经过点,.
(1)求二次函数的表达式
(2)将二次函数的图象向右平移个单位,图象经过点,求m 的值;
(3)在由(2)平移后的图象上,当时,函数的最小值为,求n的值.
24.如图,抛物线与轴交于,两点.点C为抛物线与轴交点.点为抛物线上任意一点,其横坐标为,过点作轴,点的横坐标为.
(1)求,的值;
(2)当点在抛物线上时,求的值;
(3)当线段与抛物线有两个公共点时,直接写出的取值范围.
同课章节目录
