2024-2025学年黑龙江省哈尔滨市萧红中学九年级上学期数学开学测试卷(PDF版 含答案)
文档属性
| 名称 | 2024-2025学年黑龙江省哈尔滨市萧红中学九年级上学期数学开学测试卷(PDF版 含答案) |  | |
| 格式 | |||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-01 20:49:16 | ||
图片预览


文档简介
自信来自于实力 实力来自于努力
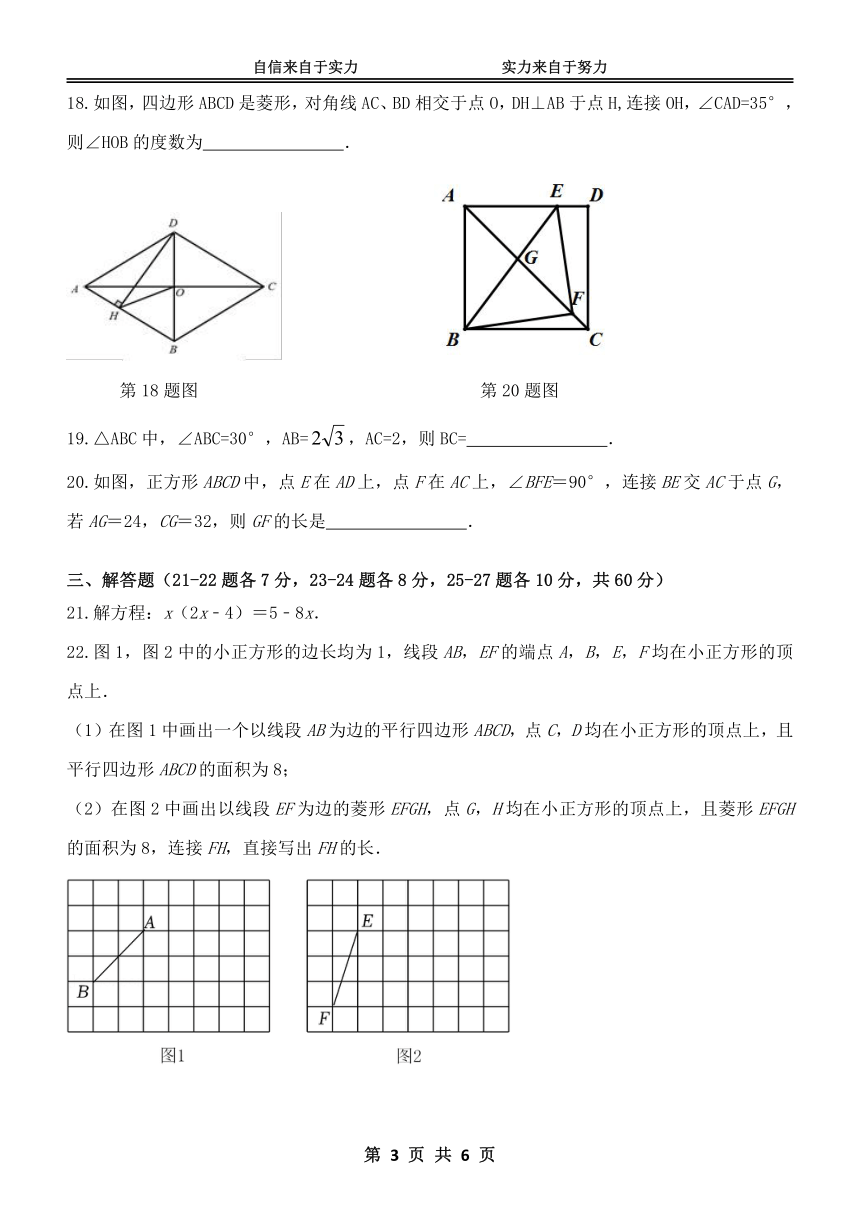
2024-2025 萧红中学九年级(上)·暑假作业验收·数学
考试时长:120 分钟 试卷满分:120 分
提 示:请将答案作答在题卡上,否则无效。
一、选择题(每小题 3 分,共 30 分)
1.下列方程中,属于一元二次方程的是( )
x 1A. +2y =1 ax2B. +bx + c = 0 C.3x + = 4 D. x2 - 2 = 0
x
2.下列各曲线中表示 y 是 x 的函数的是( )
A. B. C. D.
3.在下列长度的各组线段中,不能构成直角三角形的是( )
A.3,4,5 B.7,24,25 C.1,1, 2 D. 3, 5, 6
4.在□ABCD 中,∠A 比∠B 大 30°,则∠D的度数为( )
A.120° B.105° C.100° D.75°
5.一次函数 y=-x+3 的图象经过 ( )象限
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
6.顺次连接矩形四边中点得到的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.等腰梯形
7.某商场根据市场信息,对商场中现有空调进行两次提价,提价后的价格为提价前
的 121%,则平均每次提价的百分数为( )
A.8% B.10% C.12% D.20%
8.如图,在正方形 ABCD 外侧作等边三角形△CDE,则∠AED 的度数为( )
A.10° B.12.5° C.15° D.20°
第 1 页 共 6 页
自信来自于实力 实力来自于努力
9.给出以下四个命题:①对角线相等的四边形是矩形;②对角线互相垂直的四边形是菱形;③
对角线互相垂直的矩形是正方形;④菱形对角线的平方和等于边长平方的 4 倍.其中真命题有
( )个
A.0 B.1 C.2 D.3
10.如图,在平行四边形 ABCD 中,点 E在对角线 BD 上,EM//AD,交 AB 于点 M,EN//AB,交 AD 于点 N,
则下列式子一定正确的是( )
AM NE AM AN BC BE BD BC
A. B. C. D.
BM DE AB AD ME BD BE ME
二、填空题(每小题3分,共30分)
11.函数y x 1中,自变量 x的取值范围是 .
2
12.方程 x = 2的根是 .
13.一次函数 y (2m 6)x 5中,y随 x增大而减小,则 m的取值范围是 .
14.已知关于 x 的一元二次方程 kx 2 2x 1 0 有两个相等的实数根,则实数 k 的值
是 .
15.如下图,已知 OA=OB,BC⊥AC 于 C, C 对应的数是-2 ,AC=1,那么数轴上点 B 所表示的数
是 .
16.已知直角三角形的两边长分别为 5 和 12,则其斜边长为 .
17.如图,一次函数 y=kx+b 的图象与 x 轴交于点(4,0),与 y 轴交于点(0,2),则不等式 kx+b>0
的解集为 .
第 2 页 共 6 页
自信来自于实力 实力来自于努力
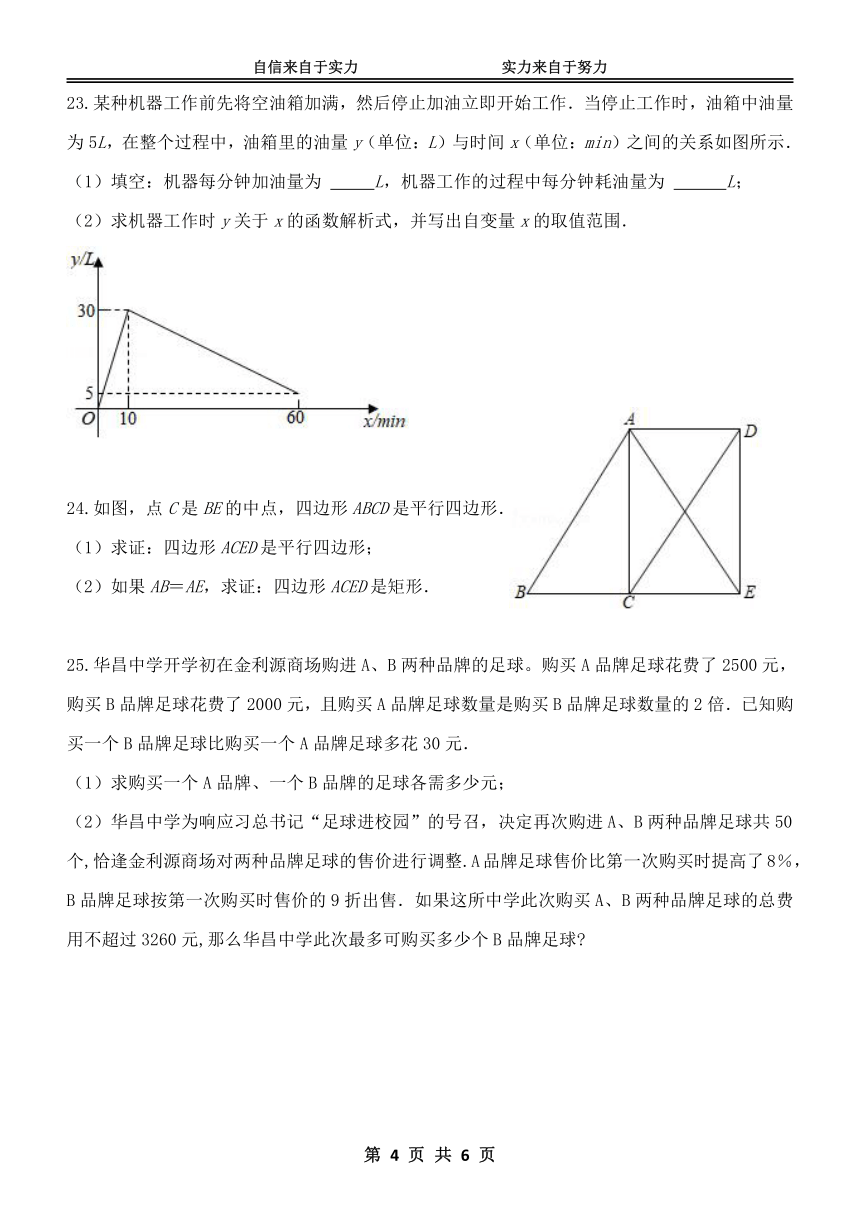
18.如图,四边形 ABCD 是菱形,对角线 AC、BD 相交于点 O,DH⊥AB 于点 H,连接 OH,∠CAD=35°,
则∠HOB 的度数为 .
第 18 题图 第 20 题图
19.△ABC 中,∠ABC=30°,AB= 2 3,AC=2,则 BC= .
20.如图,正方形 ABCD 中,点 E在 AD 上,点 F 在 AC 上,∠BFE=90°,连接 BE 交 AC 于点 G,
若 AG=24,CG=32,则 GF 的长是 .
三、解答题(21-22 题各 7 分,23-24 题各 8 分,25-27 题各 10 分,共 60 分)
21.解方程:x(2x﹣4)=5﹣8x.
22.图 1,图 2 中的小正方形的边长均为 1,线段 AB,EF 的端点 A,B,E,F 均在小正方形的顶
点上.
(1)在图 1中画出一个以线段 AB 为边的平行四边形 ABCD,点 C,D 均在小正方形的顶点上,且
平行四边形 ABCD 的面积为 8;
(2)在图 2 中画出以线段 EF 为边的菱形 EFGH,点 G,H 均在小正方形的顶点上,且菱形 EFGH
的面积为 8,连接 FH,直接写出 FH 的长.
第 3 页 共 6 页
自信来自于实力 实力来自于努力
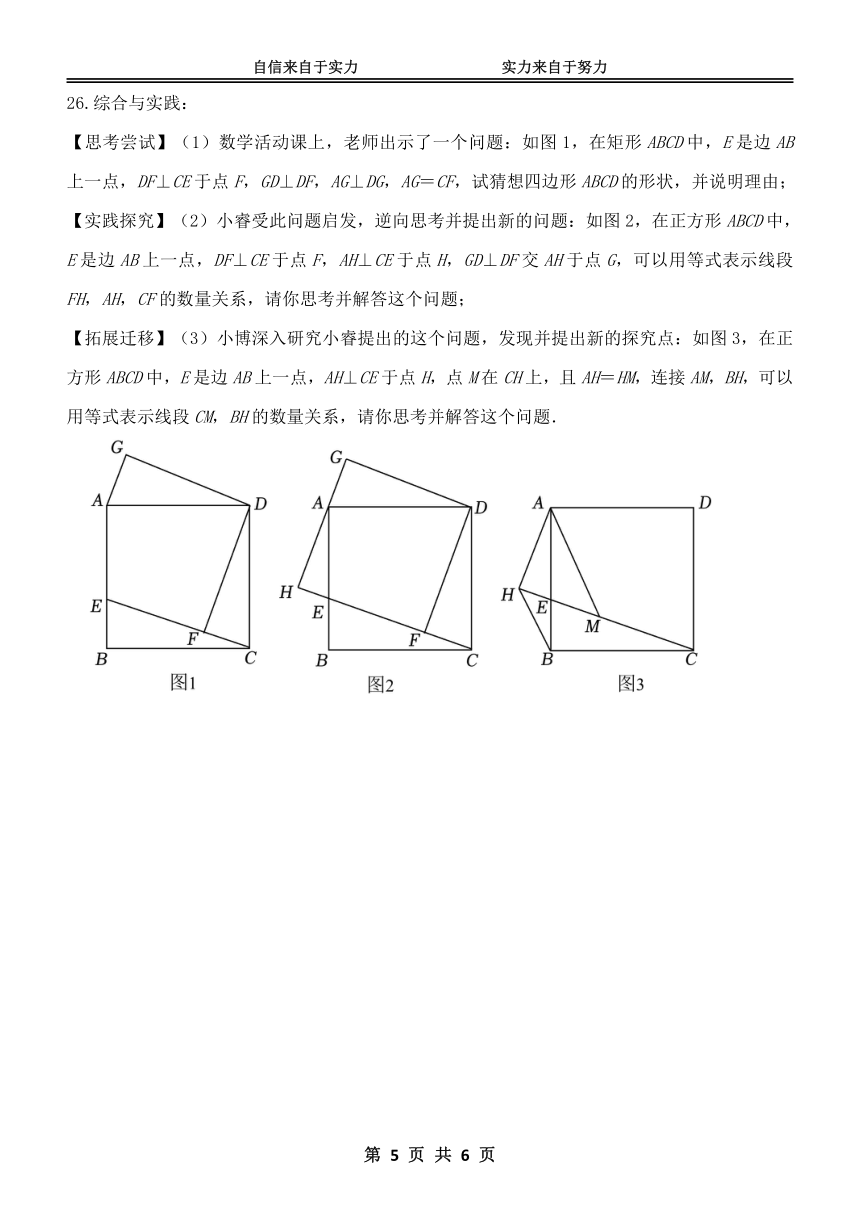
23.某种机器工作前先将空油箱加满,然后停止加油立即开始工作.当停止工作时,油箱中油量
为 5L,在整个过程中,油箱里的油量 y(单位:L)与时间 x(单位:min)之间的关系如图所示.
(1)填空:机器每分钟加油量为 L,机器工作的过程中每分钟耗油量为 L;
(2)求机器工作时 y 关于 x 的函数解析式,并写出自变量 x 的取值范围.
24.如图,点 C 是 BE 的中点,四边形 ABCD 是平行四边形.
(1)求证:四边形 ACED 是平行四边形;
(2)如果 AB=AE,求证:四边形 ACED 是矩形.
25.华昌中学开学初在金利源商场购进 A、B 两种品牌的足球。购买 A 品牌足球花费了 2500 元,
购买 B 品牌足球花费了 2000 元,且购买 A 品牌足球数量是购买 B 品牌足球数量的 2 倍.已知购
买一个 B 品牌足球比购买一个 A 品牌足球多花 30 元.
(1)求购买一个 A 品牌、一个 B 品牌的足球各需多少元;
(2)华昌中学为响应习总书记“足球进校园”的号召,决定再次购进 A、B 两种品牌足球共 50
个,恰逢金利源商场对两种品牌足球的售价进行调整.A品牌足球售价比第一次购买时提高了8%,
B品牌足球按第一次购买时售价的 9 折出售.如果这所中学此次购买 A、B 两种品牌足球的总费
用不超过 3260 元,那么华昌中学此次最多可购买多少个 B 品牌足球
第 4 页 共 6 页
自信来自于实力 实力来自于努力
26.综合与实践:
【思考尝试】(1)数学活动课上,老师出示了一个问题:如图 1,在矩形 ABCD 中,E 是边 AB
上一点,DF⊥CE 于点 F,GD⊥DF,AG⊥DG,AG=CF,试猜想四边形 ABCD 的形状,并说明理由;
【实践探究】(2)小睿受此问题启发,逆向思考并提出新的问题:如图 2,在正方形 ABCD 中,
E 是边 AB 上一点,DF⊥CE 于点 F,AH⊥CE 于点 H,GD⊥DF 交 AH 于点 G,可以用等式表示线段
FH,AH,CF 的数量关系,请你思考并解答这个问题;
【拓展迁移】(3)小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图 3,在正
方形 ABCD 中,E 是边 AB 上一点,AH⊥CE 于点 H,点 M在 CH 上,且 AH=HM,连接 AM,BH,可以
用等式表示线段 CM,BH 的数量关系,请你思考并解答这个问题.
第 5 页 共 6 页
自信来自于实力 实力来自于努力
27.已知:在平面直角坐标系中,直线 AC 交 x 轴负半轴于点 A,交 y 轴于点 C,直线 AC 的解析
式为 y= x+b(b>0),经过点 C的直线交 x轴正半轴于点 B,OB=OC,AC= .
(1)如图 1,求直线 BC 的解析式;
(2)如图 2,点 H 在 OB 上,过点 H 作 x 轴的垂线,交 BC 于点 F,点 E 在 OC 上,连接 AE 并延
长交直线 FH 于点 D,OE=BH,设直线 AE 的解析式为 y= x+5﹣t(0<t<5),线段 DF 的长
为 d,求 d与 t的函数解析式;
(3)如图 3,在(2)的条件下,连接 CD 并延长至点 M,连接 EM,∠CME=45°,过点 D 作 x
轴的平行线,交 EM 延长线于点 N,直线 BN 解析式为 y=3x﹣15,求点 N 的坐标.
第 6 页 共 6 页
2024-2025 萧红中学九年级(上)·暑假作业验收·数学答案
1 2 3 4 5
D D D D B
6 7 8 9 10
C B C C D
11 12 13 14 15
x≥1 m<3 -1
x1= 2 ,x2= 2 5
16 17 18 19 20
12 或 13 x<4 70° 4 或 2 25
21.方程化为 2x2+4x﹣5=0,
a 2 2=2,b=4,c=﹣5, Δ=b ﹣4ac=4 ﹣4×2×(﹣5)=56>0,
方程有两个不等的实数根,
∴ ,
2 14
即 , x2 2
22.(1)如图,四边形 ABCD 即为所求;
(2)如图,四边形 EFGH 即为所求.FH= =4 .
23.(1)由图象可得,
机器每分钟加油量为:30÷10=3(L),
机器工作的过程中每分钟耗油量为:(30﹣5)÷(60﹣10)=0.5(L),
故答案为:3,0.5;
(2)当 10<x≤60 时,设 y 关于 x 的函数解析式为 y=kx+b,
有图象可得: ,解得: , ∴y=﹣0.5x+35,
即机器工作时 y关于 x 的函数解析式为 y=﹣0.5x+35(10<x≤60).
24.(1)证明:∵四边形 ABCD 是平行四边形,∴AD∥BC,且 AD=BC.
∵点 C是 BE 的中点,∴BC=CE,∴AD=CE,
∵AD∥CE,∴四边形 ACED 是平行四边形;
(2)证明:∵四边形 ABCD 是平行四边形,∴AB=DC,
∵AB=AE,∴DC=AE,∵四边形 ACED 是平行四边形 ∴四边形 ACED 是矩形.
25.(1)解:设购买一个 A 品牌足球 x 元,则购买一个 B品牌足球(x+30)元
2500 2000
根据题意得 2 -----------------------2 分
x x 30
解得 x=50-------------------1 分
经检验 x=50 是原方程的解-------------------1 分
x+30=80-------------------1 分
答:购买一个 A 品牌足球需 50 元,购买一个 B 品牌足球需 80 元.
(2)解:设本次购进 a个 B品牌足球,则购进 A 品牌足球(50-a)个
根据题意得 50x(1+8%)(50-a)+80x0.9a≤ 3260--------------2 分
a 311解得 --------------1 分
9
∵a 取正整数--------------1 分 ∴a 最大值为 31
答:此次华昌中学最多可购买 31 个 B 品牌足球--------------1 分
26.解:(1)四边形 ABCD 是正方形,
理由:∵四边形 ABCD 是矩形,∴∠ADC=90°,
∵GD⊥DF,∴∠FDG=90°,∴∠ADG=∠CDF,
又∵AG=CF,∠G=∠DFC=90°,∴△ADG≌△CDF(AAS),
∴AD=CD,∴四边形 ABCD 是正方形;
(2)HF=AH+CF,
理由:∵DF⊥CE 于点 F,AH⊥CE 于点 H,GD⊥DF 交 AH 于点 G,
∴四边形 HFDG 是矩形,
∴∠G=∠DFC=90°,
∵四边形 ABCD 是正方形,∴AD=CD,∠ADC=90°,
∴∠ADG=∠CDF,∴△ADG≌△CDF(AAS),
∴AG=CF,DG=DF,∴矩形 HFDG 是正方形,
∴HG=HF=AH+AG=AH+CF;
(3)连接 AC,
∵四边形 ABCD 是正方形,∴∠BAC=45°,
∵AH⊥CE,AH=HM,
∴△AHM 是等腰直角三角形,
∴∠HAM=45°,∴∠HAB=∠MAC,
= = 2∵ ,
2
∴△AHB∽△AMC,
= = 2∴ ,
2
= 2即 BH CM.
2
27.(1)当 x=0 时, ,∴C(0,b),∴OC=b,
当 y=0 时, ,解得, ,∴ ,∴ ,
在 Rt△AOC 中,∠AOC=90°,OA2+OC2=AC2,
∴ ,解得:b=5.∴C(0,5),A(﹣2,0).
∵OB=OC,∴OB=5.∴B(5,0),
设直线 BC 的解析式为 y=kx+a(k≠0),
∴ ,解得:k=﹣1,a=5. ∴直线 BC 的解析式为:y=﹣x+5;
(2)当 y=0 时, ∴OE=5﹣t,∴BH=OE=5﹣t,
∵OB=OC,∠BOC=90°,
∴∠OBC=∠OCB=45°,
∵DH⊥x 轴,∴∠OHF=90°,∴∠HFB=45°,∴∠HFB=∠OBC,
∴FH=BH=5﹣t,∴OH=OB﹣OH=5﹣(5﹣t)=t,∴点 D 的横坐标为 t,
∴点 D的纵坐标为 ,
∴ ,
∴ ;
(3)过点 C 作 CK⊥CM,连接 FE 并延长交 CK 于点 K,连接 DK,
过点 C作 CL⊥HD 交 HD 的延长线于 L,
∵OE∥FH,OE=FH,∴四边形 EOHF 为矩形.∴EF∥x轴.
∵DN∥x 轴,∴DN∥FK,
∵四边形 EOHF 为矩形,∴∠CEF=90°,∠EFL=90°,
∵∠L=90°,∴四边形 CEFL 为矩形,
∵∠OCB=45°,∴∠EFC=90°﹣45°=45°∴∠OCB=∠EFC,
∴CE=EF,∴四边形 CEFL 为正方形,∴CE=CL,∠ECL=90°,
∵CK⊥CM,∴∠KCD=90°,∴∠KCD=∠ECL,
∴∠KCD﹣∠ECD=∠ECL﹣∠ECD,即∠KCE=∠DCL,
∵∠L=∠CEK,∴△CEK≌△CLD(ASA),∴CK=CD,KE=DL,
∴∠CKD=∠CDK=(180°﹣90°)÷2=45°,
∵∠CME=45°,∴∠CME=∠CDK,∴DK∥NE,
又∵DN∥KE,∴四边形 KEND 为平行四边形,∴DN=KE,∴DN=DL,
∵由(2)知 ,DN∥x 轴,
∴点 N的纵坐标为 ,
∵直线 BC 的解析式为 y=3x﹣15, ,
解得: ,
∴ ,
∵LH=CO=5, ,
∴ ,
∴ ,
解得:t1=4, (不合题意,舍去),
∴N(6,3).
2024-2025 萧红中学九年级(上)·暑假作业验收·数学
考试时长:120 分钟 试卷满分:120 分
提 示:请将答案作答在题卡上,否则无效。
一、选择题(每小题 3 分,共 30 分)
1.下列方程中,属于一元二次方程的是( )
x 1A. +2y =1 ax2B. +bx + c = 0 C.3x + = 4 D. x2 - 2 = 0
x
2.下列各曲线中表示 y 是 x 的函数的是( )
A. B. C. D.
3.在下列长度的各组线段中,不能构成直角三角形的是( )
A.3,4,5 B.7,24,25 C.1,1, 2 D. 3, 5, 6
4.在□ABCD 中,∠A 比∠B 大 30°,则∠D的度数为( )
A.120° B.105° C.100° D.75°
5.一次函数 y=-x+3 的图象经过 ( )象限
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
6.顺次连接矩形四边中点得到的四边形一定是( )
A.正方形 B.矩形 C.菱形 D.等腰梯形
7.某商场根据市场信息,对商场中现有空调进行两次提价,提价后的价格为提价前
的 121%,则平均每次提价的百分数为( )
A.8% B.10% C.12% D.20%
8.如图,在正方形 ABCD 外侧作等边三角形△CDE,则∠AED 的度数为( )
A.10° B.12.5° C.15° D.20°
第 1 页 共 6 页
自信来自于实力 实力来自于努力
9.给出以下四个命题:①对角线相等的四边形是矩形;②对角线互相垂直的四边形是菱形;③
对角线互相垂直的矩形是正方形;④菱形对角线的平方和等于边长平方的 4 倍.其中真命题有
( )个
A.0 B.1 C.2 D.3
10.如图,在平行四边形 ABCD 中,点 E在对角线 BD 上,EM//AD,交 AB 于点 M,EN//AB,交 AD 于点 N,
则下列式子一定正确的是( )
AM NE AM AN BC BE BD BC
A. B. C. D.
BM DE AB AD ME BD BE ME
二、填空题(每小题3分,共30分)
11.函数y x 1中,自变量 x的取值范围是 .
2
12.方程 x = 2的根是 .
13.一次函数 y (2m 6)x 5中,y随 x增大而减小,则 m的取值范围是 .
14.已知关于 x 的一元二次方程 kx 2 2x 1 0 有两个相等的实数根,则实数 k 的值
是 .
15.如下图,已知 OA=OB,BC⊥AC 于 C, C 对应的数是-2 ,AC=1,那么数轴上点 B 所表示的数
是 .
16.已知直角三角形的两边长分别为 5 和 12,则其斜边长为 .
17.如图,一次函数 y=kx+b 的图象与 x 轴交于点(4,0),与 y 轴交于点(0,2),则不等式 kx+b>0
的解集为 .
第 2 页 共 6 页
自信来自于实力 实力来自于努力
18.如图,四边形 ABCD 是菱形,对角线 AC、BD 相交于点 O,DH⊥AB 于点 H,连接 OH,∠CAD=35°,
则∠HOB 的度数为 .
第 18 题图 第 20 题图
19.△ABC 中,∠ABC=30°,AB= 2 3,AC=2,则 BC= .
20.如图,正方形 ABCD 中,点 E在 AD 上,点 F 在 AC 上,∠BFE=90°,连接 BE 交 AC 于点 G,
若 AG=24,CG=32,则 GF 的长是 .
三、解答题(21-22 题各 7 分,23-24 题各 8 分,25-27 题各 10 分,共 60 分)
21.解方程:x(2x﹣4)=5﹣8x.
22.图 1,图 2 中的小正方形的边长均为 1,线段 AB,EF 的端点 A,B,E,F 均在小正方形的顶
点上.
(1)在图 1中画出一个以线段 AB 为边的平行四边形 ABCD,点 C,D 均在小正方形的顶点上,且
平行四边形 ABCD 的面积为 8;
(2)在图 2 中画出以线段 EF 为边的菱形 EFGH,点 G,H 均在小正方形的顶点上,且菱形 EFGH
的面积为 8,连接 FH,直接写出 FH 的长.
第 3 页 共 6 页
自信来自于实力 实力来自于努力
23.某种机器工作前先将空油箱加满,然后停止加油立即开始工作.当停止工作时,油箱中油量
为 5L,在整个过程中,油箱里的油量 y(单位:L)与时间 x(单位:min)之间的关系如图所示.
(1)填空:机器每分钟加油量为 L,机器工作的过程中每分钟耗油量为 L;
(2)求机器工作时 y 关于 x 的函数解析式,并写出自变量 x 的取值范围.
24.如图,点 C 是 BE 的中点,四边形 ABCD 是平行四边形.
(1)求证:四边形 ACED 是平行四边形;
(2)如果 AB=AE,求证:四边形 ACED 是矩形.
25.华昌中学开学初在金利源商场购进 A、B 两种品牌的足球。购买 A 品牌足球花费了 2500 元,
购买 B 品牌足球花费了 2000 元,且购买 A 品牌足球数量是购买 B 品牌足球数量的 2 倍.已知购
买一个 B 品牌足球比购买一个 A 品牌足球多花 30 元.
(1)求购买一个 A 品牌、一个 B 品牌的足球各需多少元;
(2)华昌中学为响应习总书记“足球进校园”的号召,决定再次购进 A、B 两种品牌足球共 50
个,恰逢金利源商场对两种品牌足球的售价进行调整.A品牌足球售价比第一次购买时提高了8%,
B品牌足球按第一次购买时售价的 9 折出售.如果这所中学此次购买 A、B 两种品牌足球的总费
用不超过 3260 元,那么华昌中学此次最多可购买多少个 B 品牌足球
第 4 页 共 6 页
自信来自于实力 实力来自于努力
26.综合与实践:
【思考尝试】(1)数学活动课上,老师出示了一个问题:如图 1,在矩形 ABCD 中,E 是边 AB
上一点,DF⊥CE 于点 F,GD⊥DF,AG⊥DG,AG=CF,试猜想四边形 ABCD 的形状,并说明理由;
【实践探究】(2)小睿受此问题启发,逆向思考并提出新的问题:如图 2,在正方形 ABCD 中,
E 是边 AB 上一点,DF⊥CE 于点 F,AH⊥CE 于点 H,GD⊥DF 交 AH 于点 G,可以用等式表示线段
FH,AH,CF 的数量关系,请你思考并解答这个问题;
【拓展迁移】(3)小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图 3,在正
方形 ABCD 中,E 是边 AB 上一点,AH⊥CE 于点 H,点 M在 CH 上,且 AH=HM,连接 AM,BH,可以
用等式表示线段 CM,BH 的数量关系,请你思考并解答这个问题.
第 5 页 共 6 页
自信来自于实力 实力来自于努力
27.已知:在平面直角坐标系中,直线 AC 交 x 轴负半轴于点 A,交 y 轴于点 C,直线 AC 的解析
式为 y= x+b(b>0),经过点 C的直线交 x轴正半轴于点 B,OB=OC,AC= .
(1)如图 1,求直线 BC 的解析式;
(2)如图 2,点 H 在 OB 上,过点 H 作 x 轴的垂线,交 BC 于点 F,点 E 在 OC 上,连接 AE 并延
长交直线 FH 于点 D,OE=BH,设直线 AE 的解析式为 y= x+5﹣t(0<t<5),线段 DF 的长
为 d,求 d与 t的函数解析式;
(3)如图 3,在(2)的条件下,连接 CD 并延长至点 M,连接 EM,∠CME=45°,过点 D 作 x
轴的平行线,交 EM 延长线于点 N,直线 BN 解析式为 y=3x﹣15,求点 N 的坐标.
第 6 页 共 6 页
2024-2025 萧红中学九年级(上)·暑假作业验收·数学答案
1 2 3 4 5
D D D D B
6 7 8 9 10
C B C C D
11 12 13 14 15
x≥1 m<3 -1
x1= 2 ,x2= 2 5
16 17 18 19 20
12 或 13 x<4 70° 4 或 2 25
21.方程化为 2x2+4x﹣5=0,
a 2 2=2,b=4,c=﹣5, Δ=b ﹣4ac=4 ﹣4×2×(﹣5)=56>0,
方程有两个不等的实数根,
∴ ,
2 14
即 , x2 2
22.(1)如图,四边形 ABCD 即为所求;
(2)如图,四边形 EFGH 即为所求.FH= =4 .
23.(1)由图象可得,
机器每分钟加油量为:30÷10=3(L),
机器工作的过程中每分钟耗油量为:(30﹣5)÷(60﹣10)=0.5(L),
故答案为:3,0.5;
(2)当 10<x≤60 时,设 y 关于 x 的函数解析式为 y=kx+b,
有图象可得: ,解得: , ∴y=﹣0.5x+35,
即机器工作时 y关于 x 的函数解析式为 y=﹣0.5x+35(10<x≤60).
24.(1)证明:∵四边形 ABCD 是平行四边形,∴AD∥BC,且 AD=BC.
∵点 C是 BE 的中点,∴BC=CE,∴AD=CE,
∵AD∥CE,∴四边形 ACED 是平行四边形;
(2)证明:∵四边形 ABCD 是平行四边形,∴AB=DC,
∵AB=AE,∴DC=AE,∵四边形 ACED 是平行四边形 ∴四边形 ACED 是矩形.
25.(1)解:设购买一个 A 品牌足球 x 元,则购买一个 B品牌足球(x+30)元
2500 2000
根据题意得 2 -----------------------2 分
x x 30
解得 x=50-------------------1 分
经检验 x=50 是原方程的解-------------------1 分
x+30=80-------------------1 分
答:购买一个 A 品牌足球需 50 元,购买一个 B 品牌足球需 80 元.
(2)解:设本次购进 a个 B品牌足球,则购进 A 品牌足球(50-a)个
根据题意得 50x(1+8%)(50-a)+80x0.9a≤ 3260--------------2 分
a 311解得 --------------1 分
9
∵a 取正整数--------------1 分 ∴a 最大值为 31
答:此次华昌中学最多可购买 31 个 B 品牌足球--------------1 分
26.解:(1)四边形 ABCD 是正方形,
理由:∵四边形 ABCD 是矩形,∴∠ADC=90°,
∵GD⊥DF,∴∠FDG=90°,∴∠ADG=∠CDF,
又∵AG=CF,∠G=∠DFC=90°,∴△ADG≌△CDF(AAS),
∴AD=CD,∴四边形 ABCD 是正方形;
(2)HF=AH+CF,
理由:∵DF⊥CE 于点 F,AH⊥CE 于点 H,GD⊥DF 交 AH 于点 G,
∴四边形 HFDG 是矩形,
∴∠G=∠DFC=90°,
∵四边形 ABCD 是正方形,∴AD=CD,∠ADC=90°,
∴∠ADG=∠CDF,∴△ADG≌△CDF(AAS),
∴AG=CF,DG=DF,∴矩形 HFDG 是正方形,
∴HG=HF=AH+AG=AH+CF;
(3)连接 AC,
∵四边形 ABCD 是正方形,∴∠BAC=45°,
∵AH⊥CE,AH=HM,
∴△AHM 是等腰直角三角形,
∴∠HAM=45°,∴∠HAB=∠MAC,
= = 2∵ ,
2
∴△AHB∽△AMC,
= = 2∴ ,
2
= 2即 BH CM.
2
27.(1)当 x=0 时, ,∴C(0,b),∴OC=b,
当 y=0 时, ,解得, ,∴ ,∴ ,
在 Rt△AOC 中,∠AOC=90°,OA2+OC2=AC2,
∴ ,解得:b=5.∴C(0,5),A(﹣2,0).
∵OB=OC,∴OB=5.∴B(5,0),
设直线 BC 的解析式为 y=kx+a(k≠0),
∴ ,解得:k=﹣1,a=5. ∴直线 BC 的解析式为:y=﹣x+5;
(2)当 y=0 时, ∴OE=5﹣t,∴BH=OE=5﹣t,
∵OB=OC,∠BOC=90°,
∴∠OBC=∠OCB=45°,
∵DH⊥x 轴,∴∠OHF=90°,∴∠HFB=45°,∴∠HFB=∠OBC,
∴FH=BH=5﹣t,∴OH=OB﹣OH=5﹣(5﹣t)=t,∴点 D 的横坐标为 t,
∴点 D的纵坐标为 ,
∴ ,
∴ ;
(3)过点 C 作 CK⊥CM,连接 FE 并延长交 CK 于点 K,连接 DK,
过点 C作 CL⊥HD 交 HD 的延长线于 L,
∵OE∥FH,OE=FH,∴四边形 EOHF 为矩形.∴EF∥x轴.
∵DN∥x 轴,∴DN∥FK,
∵四边形 EOHF 为矩形,∴∠CEF=90°,∠EFL=90°,
∵∠L=90°,∴四边形 CEFL 为矩形,
∵∠OCB=45°,∴∠EFC=90°﹣45°=45°∴∠OCB=∠EFC,
∴CE=EF,∴四边形 CEFL 为正方形,∴CE=CL,∠ECL=90°,
∵CK⊥CM,∴∠KCD=90°,∴∠KCD=∠ECL,
∴∠KCD﹣∠ECD=∠ECL﹣∠ECD,即∠KCE=∠DCL,
∵∠L=∠CEK,∴△CEK≌△CLD(ASA),∴CK=CD,KE=DL,
∴∠CKD=∠CDK=(180°﹣90°)÷2=45°,
∵∠CME=45°,∴∠CME=∠CDK,∴DK∥NE,
又∵DN∥KE,∴四边形 KEND 为平行四边形,∴DN=KE,∴DN=DL,
∵由(2)知 ,DN∥x 轴,
∴点 N的纵坐标为 ,
∵直线 BC 的解析式为 y=3x﹣15, ,
解得: ,
∴ ,
∵LH=CO=5, ,
∴ ,
∴ ,
解得:t1=4, (不合题意,舍去),
∴N(6,3).
同课章节目录
