比例的性质
图片预览






文档简介
课件17张PPT。比例的性质对于四条线段a、b、c、d,如果其中两条线段的长度的比与另两条线段的长度的比相等,即那么这四条线段叫做成比例线段,简称
比例线段。 1.比例线段知识回顾:线段d叫作a,b,c的第四比例项
(注意a,b,c,d是有序的)
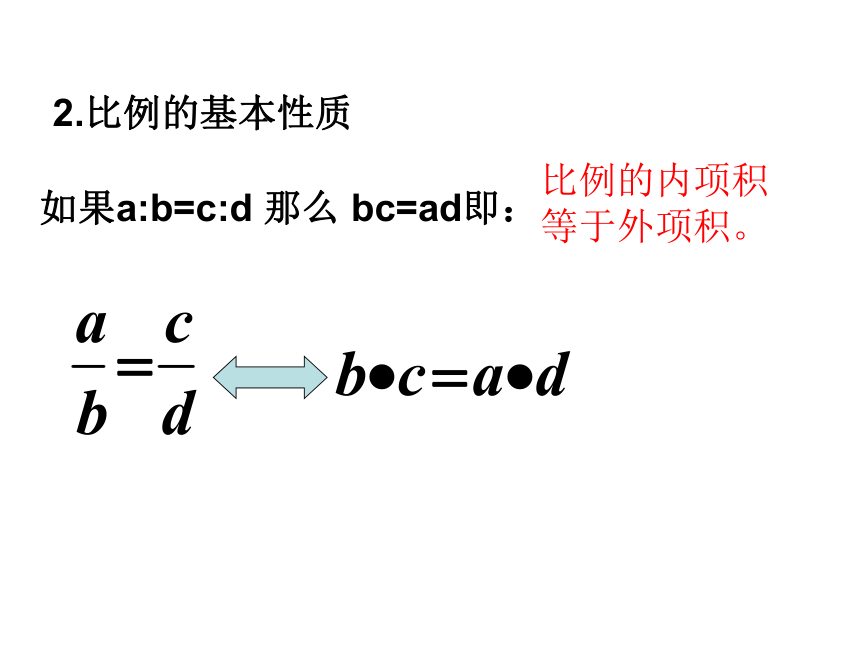
如果a:b=b:c,那么线段b叫作比例中项。2.比例的基本性质如果a:b=c:d 那么 bc=ad即:比例的内项积
等于外项积。bc=ad → →
→ (b,c作为内项)
,,,(b,c作为外项)对上一组同时交换
比的前项和后项→3.合比性质分比性质ab?bdC+da+bcd==ab?bdC-da-bd==c1.下列各线线段中,能成比例的是( )
(A)3,6,7,9(B)2,5,6,8
(C)3,6,9,18(D)1,2,3,4
2.若a=8cm,b=6cm,c=4cm,则a,b,c
的第四比例项d=___ a,c的比例中项x= __3.若(2-x):x=x:(1-x),则x=
4.在比例尺为1:10000的地图上,距离为3cm的
两地实际距离为___ 公里 巩固练习一1.若x∶(x+1)=5∶7,则x= ; 2.若 ,则 = . 3.若2a=5b,则 = , 巩固练习二a+bb=974.已知 a:b:c=2:3:5,
求 的值. a+3b–c
3a–5b+2c5.若a:b:c=2:3:7,又a+b+c=36,
求a、b 、c的值。6.如图,已知 那么 AF
AC理由:ABCEF进入新知等比定理:
=………= (b+d+…n ≠0)
= 即:若干个相等的比,其分子的和与分母的
和的比等于其中任一个比。
那么如果例1.已知: ,求 (注:另一种形式 x:y:z=3:4:5
或 x:3=y:4=z:5)解法1:设=k , ∴x=3k, y=4k, z=5k
(比例的基本性质)
= = 4∴解法2:∵ ∴ ∴= = 4
(等比定理)解法3:=∵ ∴ ∵ ∴ ∴原式 = 1+ = 4例2 已知x:y:z=2:3:4 且x+y-z=6 求 x,y,z
解:设x:y:z=2:3:4=k, ∴ x=2k , y=3k, z=4k
(碰到比例设比值)
∵x+y-z=6 ∴2k+3k-4k=6
(构造关于k的方程)
∴k=6 ∴ x=12, y=8, z=24 1.如果ab=cd 写出以a为第四比例项的比例式。
求出 ,3.若x:y:z=2:7:5 且 x-2y+3z=6 求 x,y,z的值
4.若:x:y:z=2:3:4 求 , 的值 2.若 的值巩固提高
比例线段。 1.比例线段知识回顾:线段d叫作a,b,c的第四比例项
(注意a,b,c,d是有序的)
如果a:b=b:c,那么线段b叫作比例中项。2.比例的基本性质如果a:b=c:d 那么 bc=ad即:比例的内项积
等于外项积。bc=ad → →
→ (b,c作为内项)
,,,(b,c作为外项)对上一组同时交换
比的前项和后项→3.合比性质分比性质ab?bdC+da+bcd==ab?bdC-da-bd==c1.下列各线线段中,能成比例的是( )
(A)3,6,7,9(B)2,5,6,8
(C)3,6,9,18(D)1,2,3,4
2.若a=8cm,b=6cm,c=4cm,则a,b,c
的第四比例项d=___ a,c的比例中项x= __3.若(2-x):x=x:(1-x),则x=
4.在比例尺为1:10000的地图上,距离为3cm的
两地实际距离为___ 公里 巩固练习一1.若x∶(x+1)=5∶7,则x= ; 2.若 ,则 = . 3.若2a=5b,则 = , 巩固练习二a+bb=974.已知 a:b:c=2:3:5,
求 的值. a+3b–c
3a–5b+2c5.若a:b:c=2:3:7,又a+b+c=36,
求a、b 、c的值。6.如图,已知 那么 AF
AC理由:ABCEF进入新知等比定理:
=………= (b+d+…n ≠0)
= 即:若干个相等的比,其分子的和与分母的
和的比等于其中任一个比。
那么如果例1.已知: ,求 (注:另一种形式 x:y:z=3:4:5
或 x:3=y:4=z:5)解法1:设=k , ∴x=3k, y=4k, z=5k
(比例的基本性质)
= = 4∴解法2:∵ ∴ ∴= = 4
(等比定理)解法3:=∵ ∴ ∵ ∴ ∴原式 = 1+ = 4例2 已知x:y:z=2:3:4 且x+y-z=6 求 x,y,z
解:设x:y:z=2:3:4=k, ∴ x=2k , y=3k, z=4k
(碰到比例设比值)
∵x+y-z=6 ∴2k+3k-4k=6
(构造关于k的方程)
∴k=6 ∴ x=12, y=8, z=24 1.如果ab=cd 写出以a为第四比例项的比例式。
求出 ,3.若x:y:z=2:7:5 且 x-2y+3z=6 求 x,y,z的值
4.若:x:y:z=2:3:4 求 , 的值 2.若 的值巩固提高
