初中数学人教版(2012)九年级上册21.2.1(课时2)配方法 教学课件 (共23张PPT)
文档属性
| 名称 | 初中数学人教版(2012)九年级上册21.2.1(课时2)配方法 教学课件 (共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-02 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
21.2.1配方法
第二十一章 一元二次方程
学习目标
探索利用配方法解一元二次方程的一般步骤;
能够利用配方法解一元二次方程.
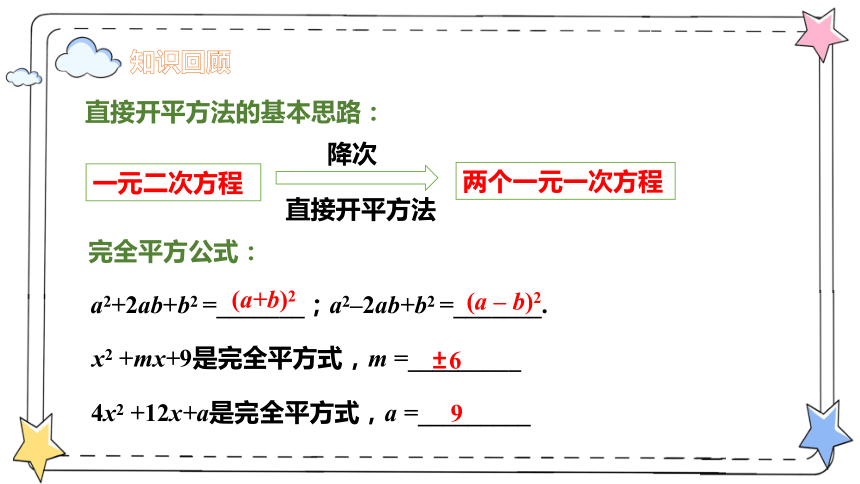
知识回顾
a2+2ab+b2 =_______;a2–2ab+b2 =_______.
直接开平方法的基本思路:
一元二次方程
两个一元一次方程
降次
直接开平方法
完全平方公式:
(a+b)2
(a – b)2
x2 +mx+9是完全平方式,m =_________
±6
4x2 +12x+a是完全平方式,a =_________
9
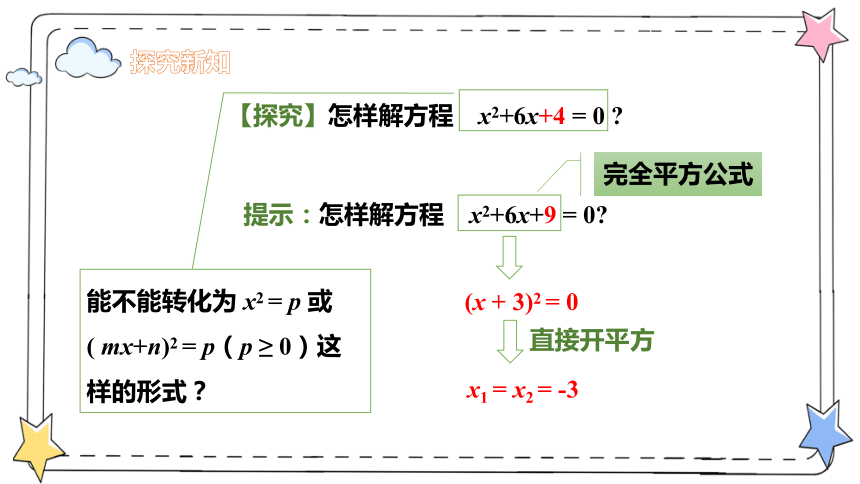
探究新知
【探究】怎样解方程 x2+6x+4 = 0
提示:怎样解方程 x2+6x+9 = 0
完全平方公式
(x + 3)2 = 0
直接开平方
x1 = x2 = -3
能不能转化为 x2 = p 或( mx+n)2 = p(p ≥ 0)这样的形式?
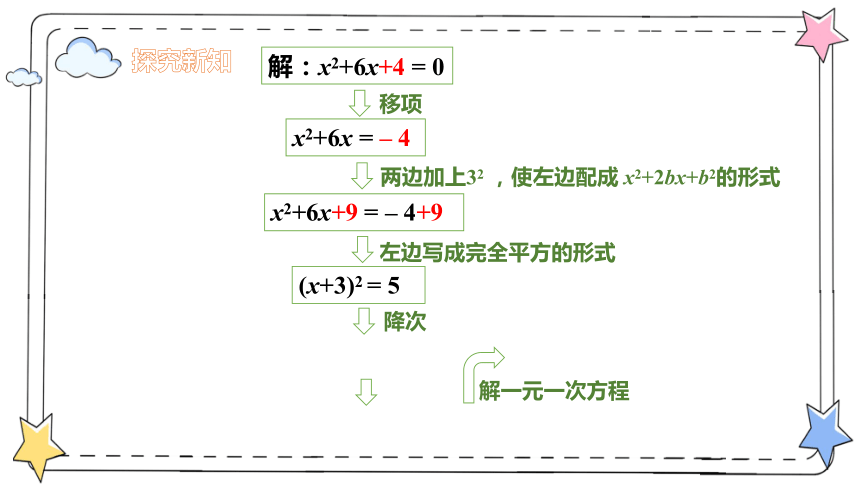
探究新知
解:x2+6x+4 = 0
x2+6x = – 4
x2+6x+9 = – 4+9
(x+3)2 = 5
移项
两边加上32 ,使左边配成 x2+2bx+b2的形式
左边写成完全平方的形式
降次
解一元一次方程
归纳总结
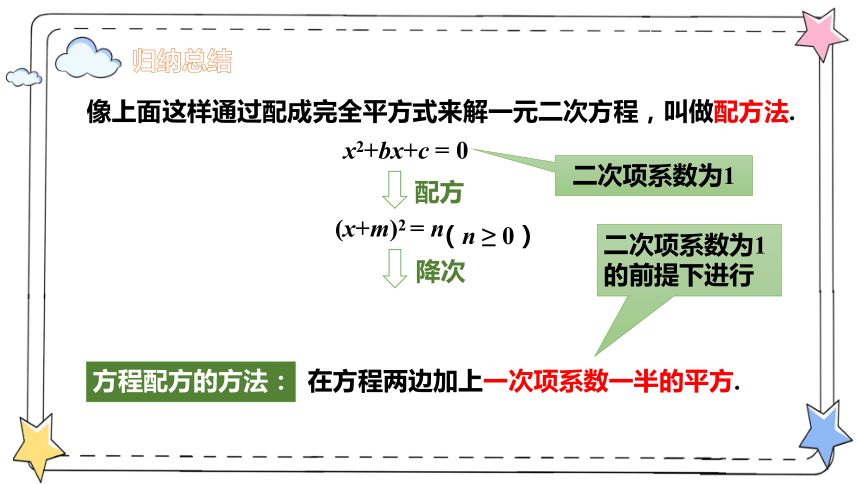
像上面这样通过配成完全平方式来解一元二次方程,叫做配方法.
x2+bx+c = 0
(x+m)2 = n
配方
降次
(n ≥ 0)
方程配方的方法:
在方程两边加上一次项系数一半的平方.
二次项系数为1
二次项系数为1的前提下进行
归纳总结
用配方法解一元二次方程的一般步骤:
①把方程化为一般形式;
②把方程的常数项通过移项移到方程的右边;
③方程两边同时除以二次项系数a;
④方程两边同时加上一次项系数一半的平方;
⑤此时方程的左边是一个完全平方式,然后利用平方根的定义把一元二次方程化为两个一元一次方程来解;
⑥定解.
例题练习
解下列方程:
【分析】(1)方程的二次项系数为1,直接运用配方法.
x2 – 8x = – 1
配方,得
(x– 4)2 = 15
x2 – 8x +42 = – 1+42
由此可得
(1) x2 – 8x+1 = 0
(2) 2x2 +1 = 3x
(3) 3x2 – 6x+4 = 0
解:(1) 移项,得
例题练习
【分析】(2)先把方程化为2x2 - 3x+1= 0.它的二次项系数是2,为便于配方,将二次项系数化为1,为此方程两边都除以2.
解:移项,得
2x2 – 3x = – 1
二项式系数化为1,得
配方,得
由此可得
例题练习
【分析】(3)二次项系数为3,先将二次项系数化为1,方程两边都除以3后再配方.
解:移项,得
3x2 – 6x = – 4
二项式系数化为1,得
配方,得
因为 ,而 <0,
即原方程无实数根.
p 的取值范围 方程根的情况
归纳总结
一般地,如果一个一元二次方程通过配方转化成 (x+n)2 = p 的形式,那么就有:
p > 0
p = 0
p < 0
两个相等实数根 x1 = x2 = – n
无实数根
两个不相等实数根
B
A
D
A
C
②
小结
步骤:
概念:
通过配成完全平方形式来解一元二次方程的方法,叫做配方法.
(1)化;(2)移项;(3)配方;(4)开方(5)求解;(6)定解.
形如(x+n)2=p的方程的根的情况
p 的取值范围 方程根的情况
p > 0
p = 0
p < 0
两个相等实数根 x1 = x2 = – n
无实数根
两个不相等实数根
谢谢各位同学的观看
21.2.1配方法
第二十一章 一元二次方程
学习目标
探索利用配方法解一元二次方程的一般步骤;
能够利用配方法解一元二次方程.
知识回顾
a2+2ab+b2 =_______;a2–2ab+b2 =_______.
直接开平方法的基本思路:
一元二次方程
两个一元一次方程
降次
直接开平方法
完全平方公式:
(a+b)2
(a – b)2
x2 +mx+9是完全平方式,m =_________
±6
4x2 +12x+a是完全平方式,a =_________
9
探究新知
【探究】怎样解方程 x2+6x+4 = 0
提示:怎样解方程 x2+6x+9 = 0
完全平方公式
(x + 3)2 = 0
直接开平方
x1 = x2 = -3
能不能转化为 x2 = p 或( mx+n)2 = p(p ≥ 0)这样的形式?
探究新知
解:x2+6x+4 = 0
x2+6x = – 4
x2+6x+9 = – 4+9
(x+3)2 = 5
移项
两边加上32 ,使左边配成 x2+2bx+b2的形式
左边写成完全平方的形式
降次
解一元一次方程
归纳总结
像上面这样通过配成完全平方式来解一元二次方程,叫做配方法.
x2+bx+c = 0
(x+m)2 = n
配方
降次
(n ≥ 0)
方程配方的方法:
在方程两边加上一次项系数一半的平方.
二次项系数为1
二次项系数为1的前提下进行
归纳总结
用配方法解一元二次方程的一般步骤:
①把方程化为一般形式;
②把方程的常数项通过移项移到方程的右边;
③方程两边同时除以二次项系数a;
④方程两边同时加上一次项系数一半的平方;
⑤此时方程的左边是一个完全平方式,然后利用平方根的定义把一元二次方程化为两个一元一次方程来解;
⑥定解.
例题练习
解下列方程:
【分析】(1)方程的二次项系数为1,直接运用配方法.
x2 – 8x = – 1
配方,得
(x– 4)2 = 15
x2 – 8x +42 = – 1+42
由此可得
(1) x2 – 8x+1 = 0
(2) 2x2 +1 = 3x
(3) 3x2 – 6x+4 = 0
解:(1) 移项,得
例题练习
【分析】(2)先把方程化为2x2 - 3x+1= 0.它的二次项系数是2,为便于配方,将二次项系数化为1,为此方程两边都除以2.
解:移项,得
2x2 – 3x = – 1
二项式系数化为1,得
配方,得
由此可得
例题练习
【分析】(3)二次项系数为3,先将二次项系数化为1,方程两边都除以3后再配方.
解:移项,得
3x2 – 6x = – 4
二项式系数化为1,得
配方,得
因为 ,而 <0,
即原方程无实数根.
p 的取值范围 方程根的情况
归纳总结
一般地,如果一个一元二次方程通过配方转化成 (x+n)2 = p 的形式,那么就有:
p > 0
p = 0
p < 0
两个相等实数根 x1 = x2 = – n
无实数根
两个不相等实数根
B
A
D
A
C
②
小结
步骤:
概念:
通过配成完全平方形式来解一元二次方程的方法,叫做配方法.
(1)化;(2)移项;(3)配方;(4)开方(5)求解;(6)定解.
形如(x+n)2=p的方程的根的情况
p 的取值范围 方程根的情况
p > 0
p = 0
p < 0
两个相等实数根 x1 = x2 = – n
无实数根
两个不相等实数根
谢谢各位同学的观看
同课章节目录
