八年级上册 勾股定理1(华师大版)
文档属性
| 名称 | 八年级上册 勾股定理1(华师大版) |

|
|
| 格式 | rar | ||
| 文件大小 | 926.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-08 00:00:00 | ||
图片预览



文档简介
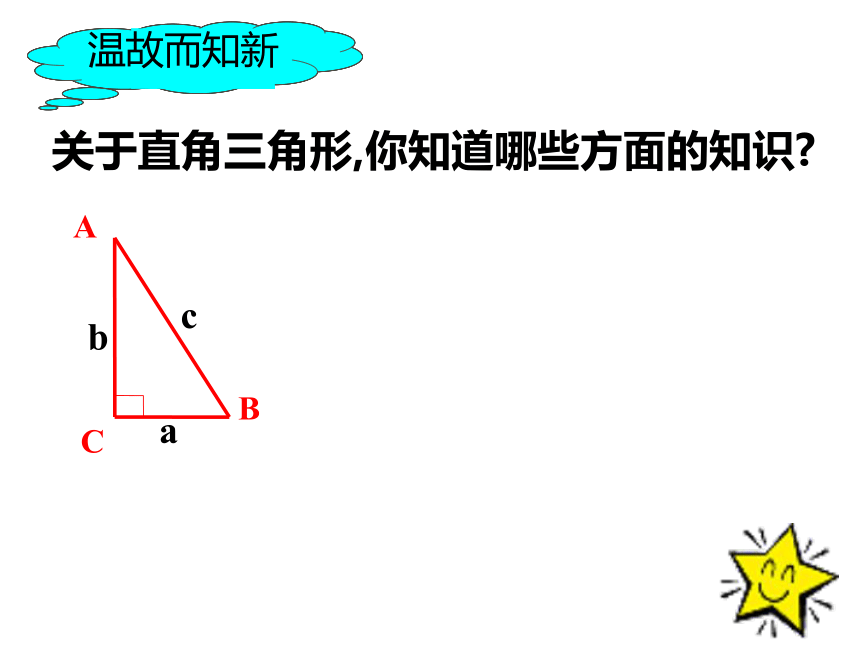
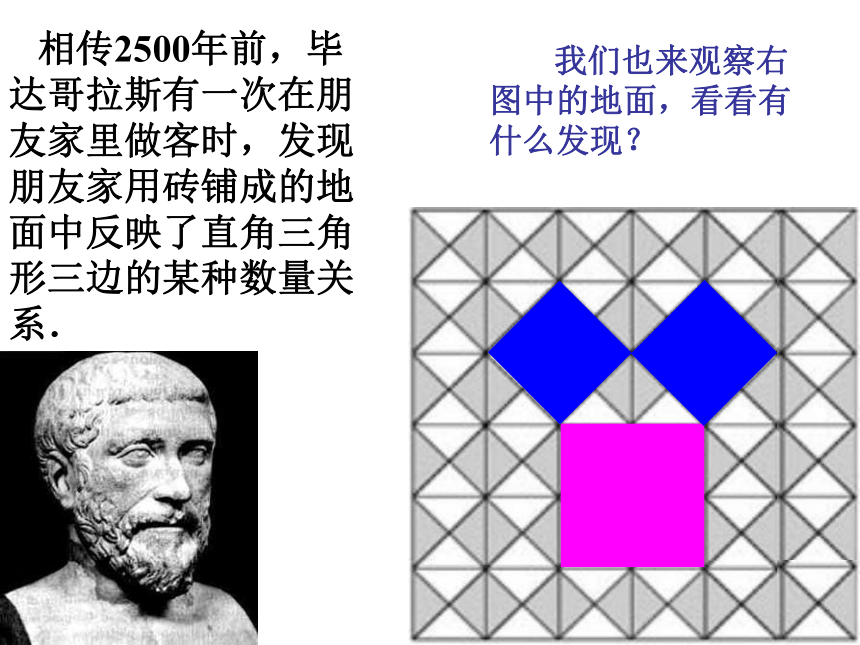
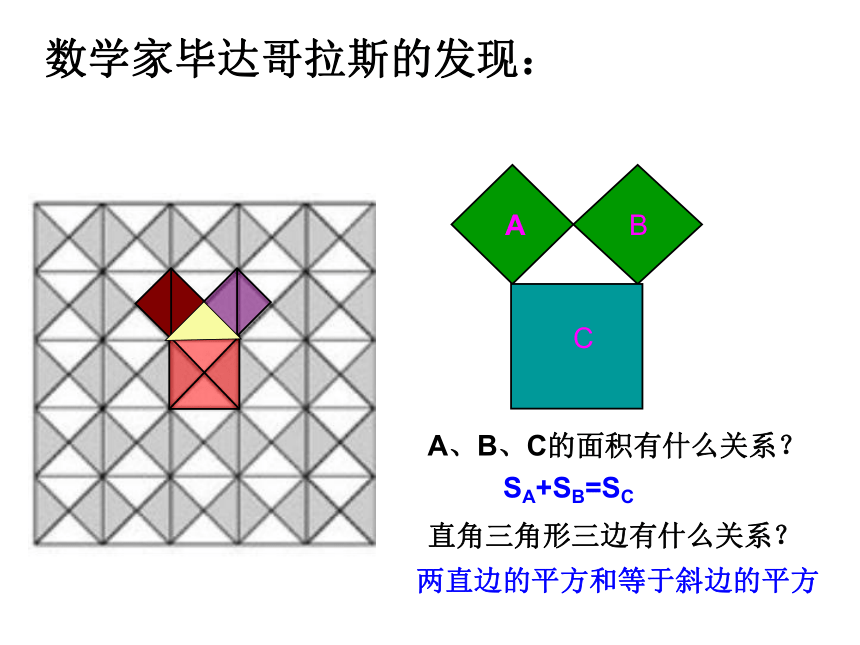
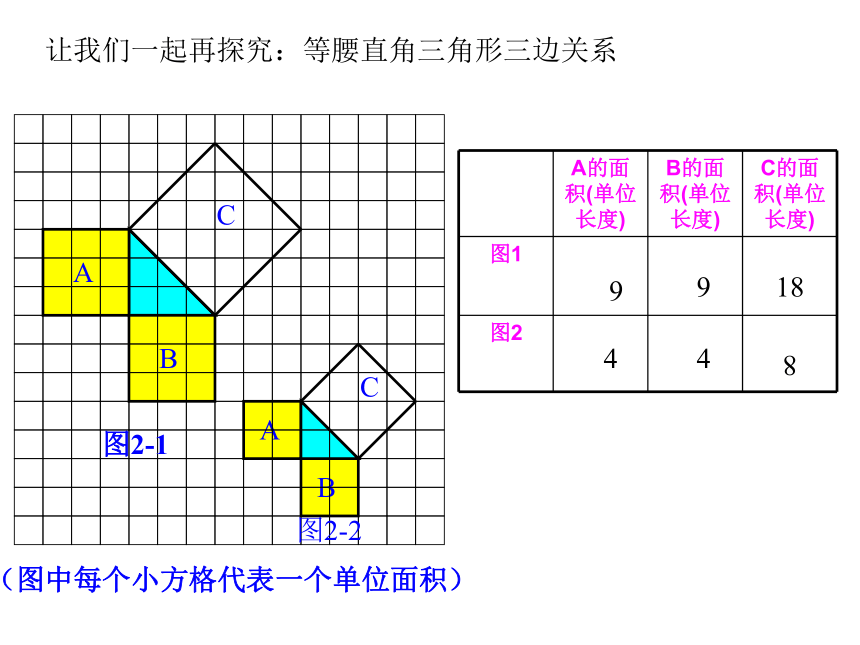
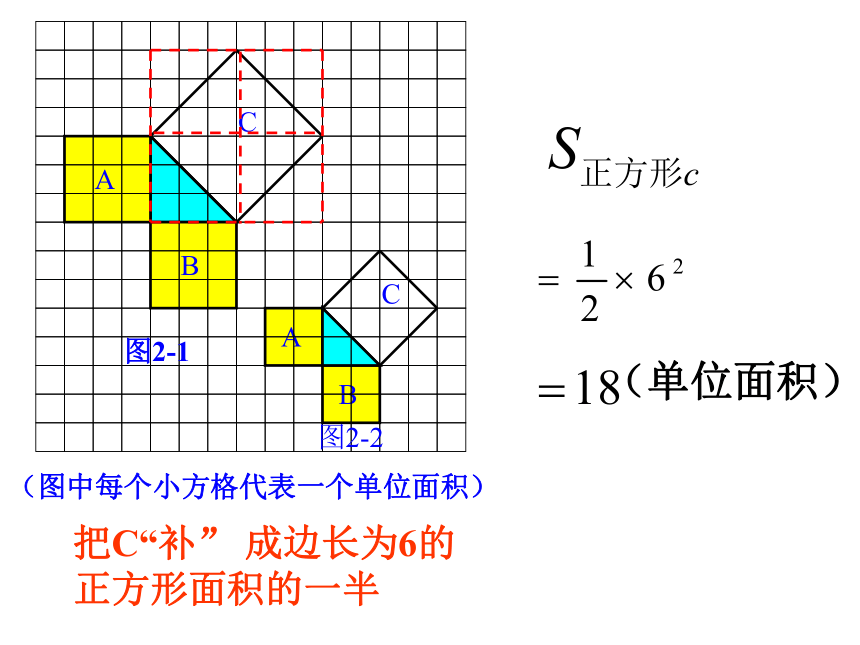
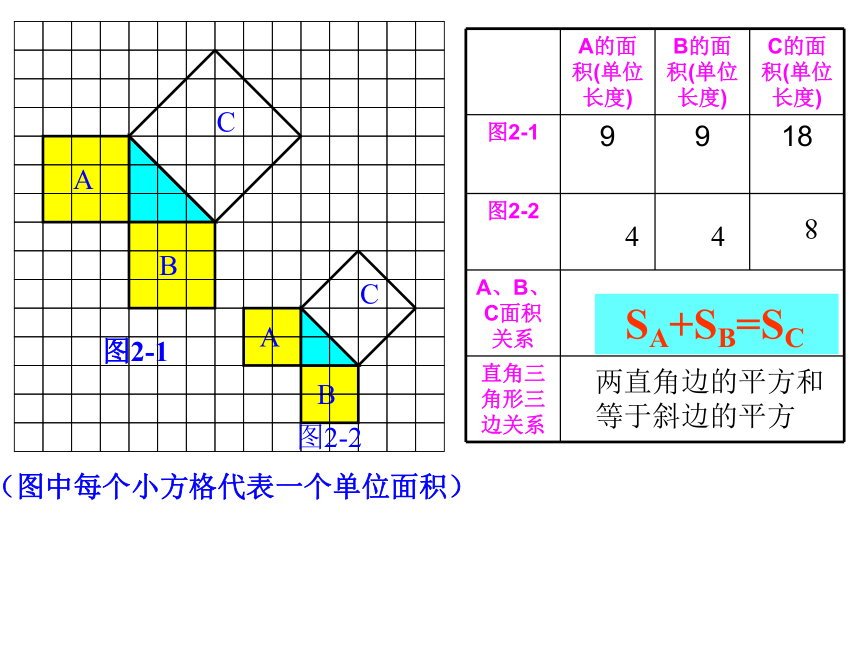
课件38张PPT。勾股定理——直角三角形三边的关系你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”.这就是本届大会会徽的图案.关于直角三角形,你知道哪些方面的知识?温故而知新 相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系. 我们也来观察右图中的地面,看看有什么发现?数学家毕达哥拉斯的发现:A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方让我们一起再探究:等腰直角三角形三边关系9918448分“割”成若干个直角边为整数的三角形(单位面积)(单位面积)把C“补” 成边长为6的正方形面积的一半 SA+SB=SC448两直角边的平方和
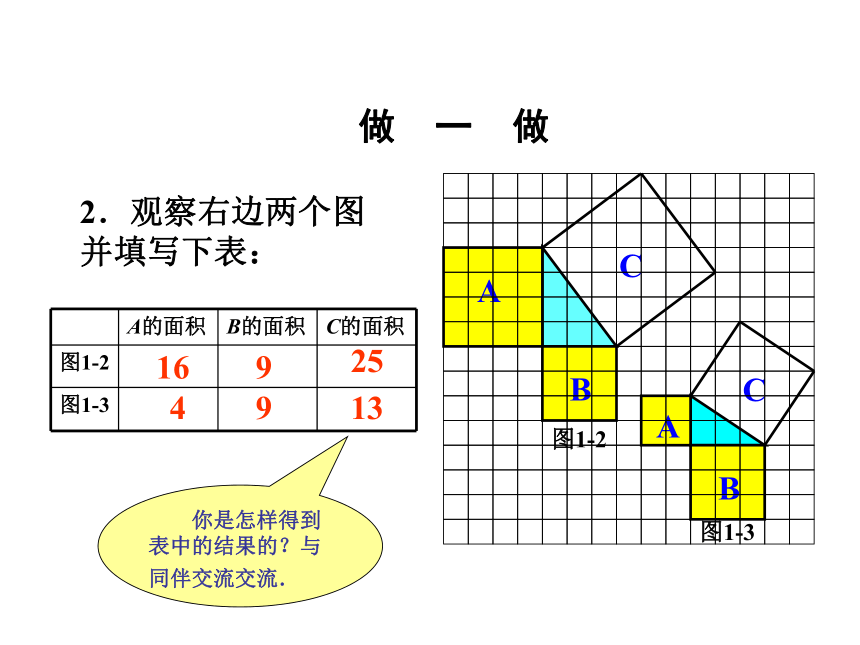
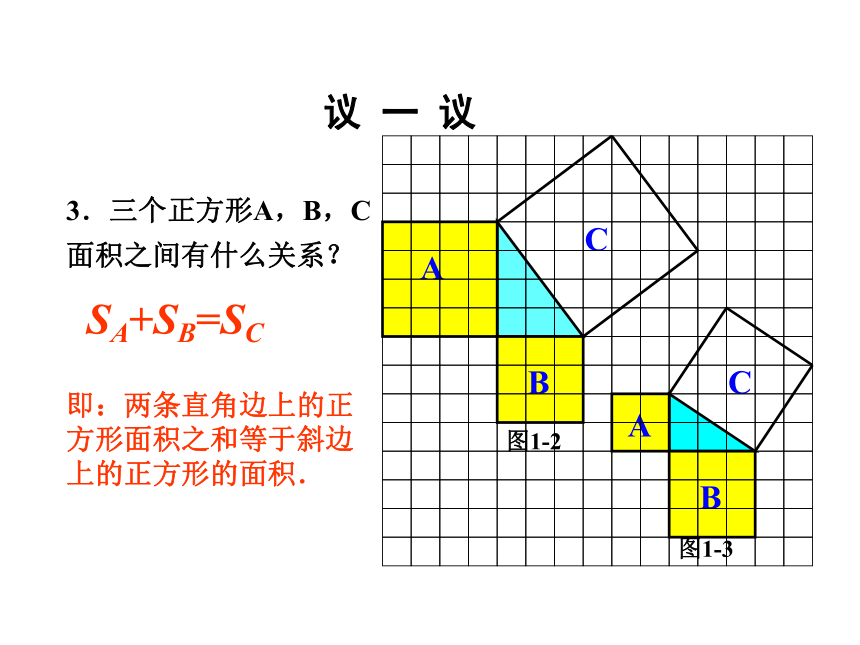
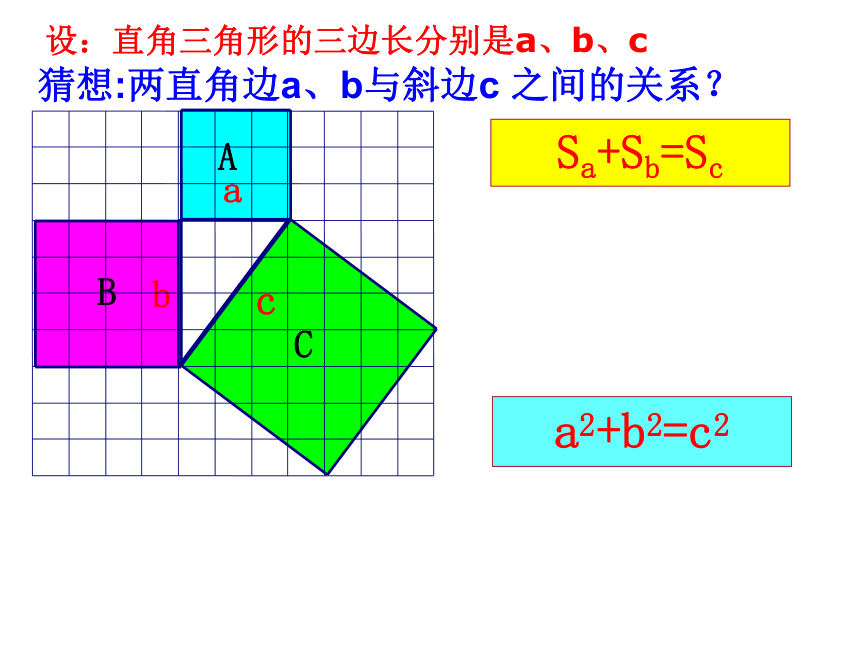
等于斜边的平方2.观察右边两个图并填写下表:169254913 你是怎样得到表中的结果的?与同伴交流交流.做 一 做3.三个正方形A,B,C面积之间有什么关系?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.议 一 议acbSa+Sb=Sc设:直角三角形的三边长分别是a、b、c猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2数学家毕达哥拉斯的故事A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方对于等腰直角三角形有这样的性质:
两直边的平方和等于斜边的平方那么对于一般的直角三角形是否也有这样的性质呢?请大家画一个任意的直角三角形,量一量,算一算。命题1:如果直角三角形的两直角边长分别为a、b,斜边
长为c,那么a2+b2=c2。分“割”成若干个直角边为整数的三角形(单位面积)(单位面积)把C“补” 成边长为6的正方形面积的一半在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 有趣的总统证法? a2 + b2 = c2a2b2a2c2对比两个图形,你能直接观察验证出勾股定理吗? abc无字证明青出华罗庚青朱出入图结论变形直角三角形中,两直角边的平方和等于斜边的平方;
c2=a2 + b2例.求出下列直角三角形中未知边的长度5x13学以致用,做一做解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2X2 =36+64x2 =100x2=62+82∴ x=10 ∵x>0 x2+52=132 x2=132-52x2=144∴ x=12(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2∵x>0ACBACB某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队能否进入三楼灭火?
1.在△ABC中, ∠C=90°,a=6,b=8,
则c=____2.在△ABC中, a=6,b=8,试求第三边c的值3.在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________1010 练一练或815A49B254.求下列图中字母所代表的
正方形的面积书山有路结论:S1+S2+S3+S4=S5+S6=S7学海无涯练习:求下列阴影部分的面积:
(1) 阴影部分是正方形; (2) 阴影部分是长方形; (3) 阴影部分是半圆.13cm12cm?cm 练习1:一架2.5米长的梯子靠在一座建筑物上,梯子的底部离建筑物0.7米,如果梯子的顶部滑下0.4米,梯子的底部向外滑出多远? 例:如图,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底边的垂直距离AB。 (精确到0.01米) 1、在Rt△ABC中, AB=c, BC=a, AC=b, ∠B=90°.
(1) 已知a=6, b=10, 求c;
(2) 已知a=24, c=25, 求b.
2、如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?(精确到0.1厘米)
3、若直角三角形的三边长分别为2、 4、 x,试求出x的所有可能值. 1.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做做一做: P62540026xP的面积 =______________X=____________225BACAB=__________AC=__________BC=__________251520比一比看看谁算得快!2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做课后探索 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。C他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走 1千米就找到宝藏,问登 陆点A到宝藏埋藏点B的 直线距离是多少千米? 练习2:假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),例:如图,小方格都是边长为1的正方形,求四边形ABCD的面积与周长.(精确到0.1) 练习:利用勾股定理,分别画出长度为 厘米和 厘米的线段. 美丽的勾股树
等于斜边的平方2.观察右边两个图并填写下表:169254913 你是怎样得到表中的结果的?与同伴交流交流.做 一 做3.三个正方形A,B,C面积之间有什么关系?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.议 一 议acbSa+Sb=Sc设:直角三角形的三边长分别是a、b、c猜想:两直角边a、b与斜边c 之间的关系?a2+b2=c2数学家毕达哥拉斯的故事A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方对于等腰直角三角形有这样的性质:
两直边的平方和等于斜边的平方那么对于一般的直角三角形是否也有这样的性质呢?请大家画一个任意的直角三角形,量一量,算一算。命题1:如果直角三角形的两直角边长分别为a、b,斜边
长为c,那么a2+b2=c2。分“割”成若干个直角边为整数的三角形(单位面积)(单位面积)把C“补” 成边长为6的正方形面积的一半在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。 有趣的总统证法? a2 + b2 = c2a2b2a2c2对比两个图形,你能直接观察验证出勾股定理吗? abc无字证明青出华罗庚青朱出入图结论变形直角三角形中,两直角边的平方和等于斜边的平方;
c2=a2 + b2例.求出下列直角三角形中未知边的长度5x13学以致用,做一做解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2X2 =36+64x2 =100x2=62+82∴ x=10 ∵x>0 x2+52=132 x2=132-52x2=144∴ x=12(2)在Rt△ABC中,由勾股定理:AB2+AC2=BC2∵x>0ACBACB某楼房三楼失火,消防队员赶来救火,了解到每层楼高3米,消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离是2.5米,请问消防队能否进入三楼灭火?
1.在△ABC中, ∠C=90°,a=6,b=8,
则c=____2.在△ABC中, a=6,b=8,试求第三边c的值3.在一个直角三角形中, 两边长分别为6、
8,则第三边的长为________1010 练一练或815A49B254.求下列图中字母所代表的
正方形的面积书山有路结论:S1+S2+S3+S4=S5+S6=S7学海无涯练习:求下列阴影部分的面积:
(1) 阴影部分是正方形; (2) 阴影部分是长方形; (3) 阴影部分是半圆.13cm12cm?cm 练习1:一架2.5米长的梯子靠在一座建筑物上,梯子的底部离建筑物0.7米,如果梯子的顶部滑下0.4米,梯子的底部向外滑出多远? 例:如图,将长为5.41米的梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底边的垂直距离AB。 (精确到0.01米) 1、在Rt△ABC中, AB=c, BC=a, AC=b, ∠B=90°.
(1) 已知a=6, b=10, 求c;
(2) 已知a=24, c=25, 求b.
2、如果一个直角三角形的两条边长分别是3厘米和4厘米,那么这个三角形的周长是多少厘米?(精确到0.1厘米)
3、若直角三角形的三边长分别为2、 4、 x,试求出x的所有可能值. 1.求下列图中表示边的未知数x、y、z的值.①81144xyz②③做一做做一做: P62540026xP的面积 =______________X=____________225BACAB=__________AC=__________BC=__________251520比一比看看谁算得快!2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x做一做课后探索 做一个长,宽,高分别为50厘米,40厘米,30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明。C他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,再折向北走到6千米处往东一拐,仅走 1千米就找到宝藏,问登 陆点A到宝藏埋藏点B的 直线距离是多少千米? 练习2:假期中,王强和同学到某海岛上去探宝旅游,按照探宝图(如图),例:如图,小方格都是边长为1的正方形,求四边形ABCD的面积与周长.(精确到0.1) 练习:利用勾股定理,分别画出长度为 厘米和 厘米的线段. 美丽的勾股树
