人教九上:专题十二 概率相关概念及必考题型过关(含解析)
文档属性
| 名称 | 人教九上:专题十二 概率相关概念及必考题型过关(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-02 22:12:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题十二 概率相关概念及必考题型过关
一、单选题
1.在一个不透明的袋子中装有除颜色外无其他差别的3个红球,2个白球,从袋子中随机摸出3个球,下列事件为必然事件的是( ).
A.至少有1个是白球 B.至少有1个是红球
C.至少有2个是红球 D.至少有2个是白球
2.“翻开人教版《数学》九年级下册课本恰好翻到第56页”这个事件是( )
A.随机事件 B.必然事件 C.不可能事件 D.无法确定
3.有两个事件,事件(1):随意翻到一本书的某页,这页的页码是奇数;事件(2):射击运动员射击一次,命中靶心.下列判断正确的是( )
A.(1)(2)都是随机事件 B.(1)(2)都是必然事件
C.(1)是必然事件,(2)是随机事件 D.(1)是随机事件,(2)是必然事件
4.经过某十字路口的汽车可能直行也可能左转或者右转.如果这三种可能性大小相同,当三辆汽车经过这个十字路口时,只有一辆汽车向左转的概率是( )
A. B. C. D.
5.不透明的袋子里装有8个小球,其中5个红色,3个蓝色,则下列说法不正确的是( )
A.从中随机抽取1个球,抽到红色的可能性更大
B.从中随机抽取1个球,抽到红色和蓝色的可能性一样大
C.从中随机抽取6个球,一定有蓝色的
D.从中随机抽取5个球,可能都是红色的
6.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,则三辆汽车经过这个十字路口时,至少有两辆车直行的概率为( )
A. B. C. D.
7.“经过有交通信号灯的路口,遇到黄灯”这个事件是( )
A.确定性事件 B.随机事件 C.不可能事件 D.必然事件
8.下列描述的事件中,是随机事件的为( )
A.旭日东升 B.心想事成 C.水中捞月 D.只手遮天
9.如果一个三位数中任意两个相邻数字之差的绝对值不超过1,则称该三位数为“关联数”.用1,2,3这三个数字随机组成一个无重复数字的三位数,恰好是“关联数”的概率( )
A. B. C. D.
10.下列词语所描述的事件属于随机事件的是( )
A.拔苗助长 B.刻舟求剑 C.守株待兔 D.竹篮打水
11.同时抛掷三枚质地均匀的硬币,恰有两枚硬币反面向上的概率是( )
A. B. C. D.
12.通常温度降到0℃以下,纯净的水结冰.这个事件是( )
A.必然事件 B.不可能事件 C.随机事件 D.确定性事件
13.甲、乙两名同学在一次用频率去估计概率的试验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )
A.从一个装有个白球和个红球的袋子中任取一球,取到红球
B.掷一枚正六面体的骰子,出现点
C.抛一枚硬币,出现正面
D.任意写一个整数,它能被整除
14.有两把不同的锁和三把钥匙,其中两把钥匙分别能打开这两把锁,第三把钥匙不能打开这两把锁,随机取出一把钥匙开任意一把锁,一次打开锁的概率是( )
A. B. C. D.
15.某批羽毛球的质量检验结果如下:
抽取的羽毛球数a 100 200 400 600 800 1000 1200
优等品的频数b 93 192 380 561 752 941 1128
优等品的频率 0.930 0.960 0.950 0.935 0.940 0.941 0.940
小明估计,从这批羽毛球中任意抽取的一只羽毛球是优等品的概率是0.94.下列说法中,正确的是( )
A.如果继续对这批羽毛球进行质量检验,优等品的频率将在0.94附近摆动
B.从这批羽毛球中任意抽取一只,一定是优等品
C.从这批羽毛球中任意抽取50只,优等品有47只
D.从这批羽毛球中任意抽取1100只,优等品的频率在0.940~0.941的范围内
16.“守株待兔”这个事件是( )
A.随机事件 B.确定性事件 C.必然事件 D.不可能事件
17.四张背面完全相同的卡片上分别写有1、2、3、4四个数字,把卡片背面朝上洗匀后,王明从这四张卡片中随机选两张,则王明选中的卡片中有偶数的概率是( )
A. B. C. D.
18.盒子里有个球,它们只有颜色不同,其中红球有6个,黄球有3个,黑球有1个.小军从中任意摸一个球,下面说法正确的是( )
A.一定是红球 B.摸出红球的可能性最大
C.不可能是黑球 D.摸出黄球的可能性最小
19.星期一上午班级共有4节课,分别为数学、语文、外语和历史,如果随机排课,那么第一节上数学课,第四节上语文课的概率为( )
A. B. C. D.
20.不透明袋子中有除颜色外完全相同的4个黑球和2个白球,从袋子中随机摸出3个球,下列事件是必然事件的是( ).
A.3个都是黑球 B.2个黑球1个白球
C.2个白球1个黑球 D.至少有1个黑球
21.下列事件中、属于不可能事件的是( )
A.打开电视机、正在直接足球比赛 B.在只装有2个玻璃球球的袋中摸出一个球是黑球
C.掷一次骰子,向上的一面出现的点数大于7 D.当室外温度低于时,一碗清水在室外会结冰
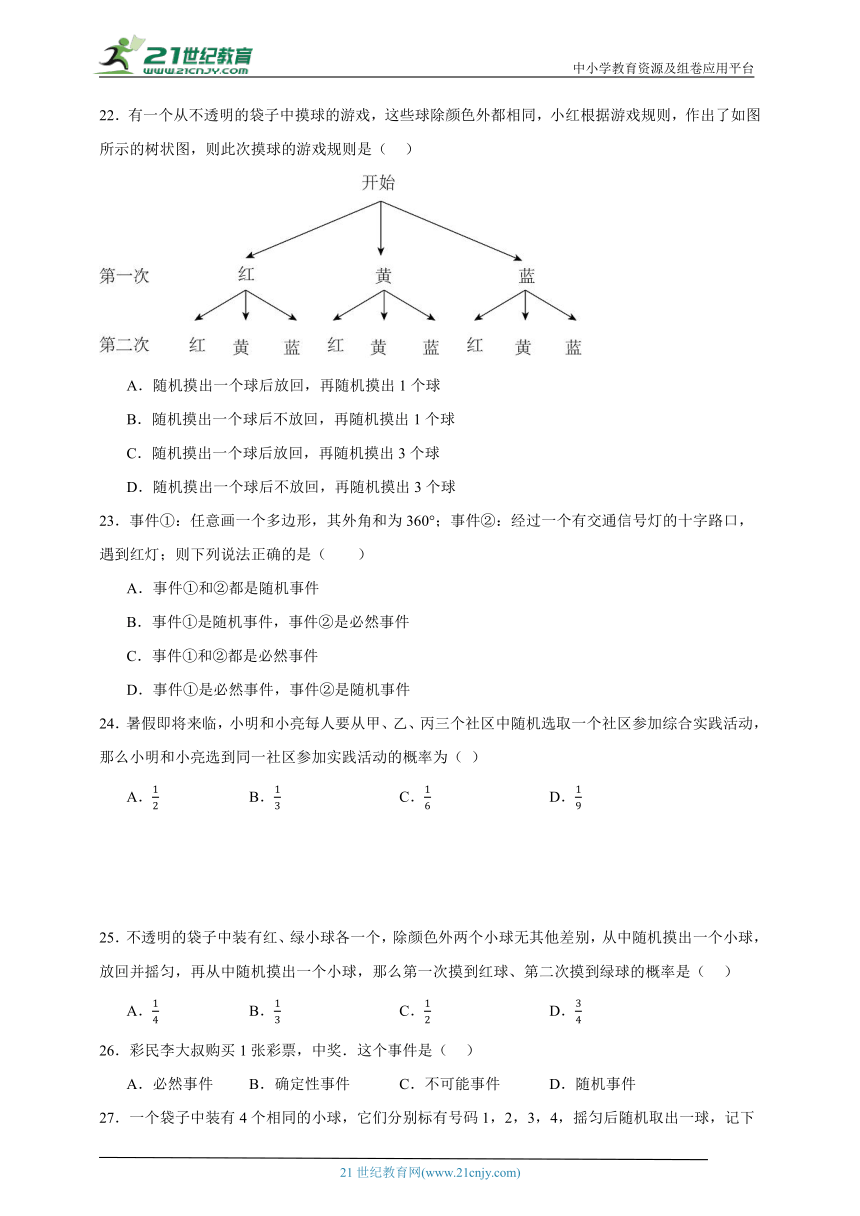
22.有一个从不透明的袋子中摸球的游戏,这些球除颜色外都相同,小红根据游戏规则,作出了如图所示的树状图,则此次摸球的游戏规则是( )
A.随机摸出一个球后放回,再随机摸出1个球
B.随机摸出一个球后不放回,再随机摸出1个球
C.随机摸出一个球后放回,再随机摸出3个球
D.随机摸出一个球后不放回,再随机摸出3个球
23.事件①:任意画一个多边形,其外角和为360°;事件②:经过一个有交通信号灯的十字路口,遇到红灯;则下列说法正确的是( )
A.事件①和②都是随机事件
B.事件①是随机事件,事件②是必然事件
C.事件①和②都是必然事件
D.事件①是必然事件,事件②是随机事件
24.暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加实践活动的概率为( )
A. B. C. D.
25.不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )
A. B. C. D.
26.彩民李大叔购买1张彩票,中奖.这个事件是( )
A.必然事件 B.确定性事件 C.不可能事件 D.随机事件
27.一个袋子中装有4个相同的小球,它们分别标有号码1,2,3,4,摇匀后随机取出一球,记下号码后放回;再将小球摇匀,并从袋中随机取出一球,则第二次取出的球的号码不小于第一次取出的球的号码的概率为( )
A. B. C. D.
28.关于下列事件:(1)通常温度降到以下,纯净的水结冰;(2)随意翻到一本书的某页,页码是奇数;(3)明天太阳从东方升起;(4)购买1张彩票,中奖;描述正确的是( )
A.(1)(2)是随机事件,(3)(4)是必然事件
B.(1)(3)是随机事件,(2)(4)是必然事件
C.(1)(3)是必然事件,(2)(4)是随机事件
D.(1)(4)是必然事件,(2)(3)是随机事件
29.抛掷一枚质地均匀的硬币三次,恰有两次正面向上的概率是( )
A. B. C. D.
30.有两个事件,事件(1):购买1张福利彩票,中奖;事件(2):掷一枚六个面的点数分别为1,2,3,4,5,6的骰子,向上一面的点数不大于6.下列判断正确的是( )
A.(1)(2)都是随机事件 B.(1)(2)都是必然事件
C.(1)是必然事件,(2)是随机事件 D.(1)是随机事件,(2)是必然事件
31.童威把三张形状大小相同但画面不同的风景图片都按相同的方式剪成相同的三段,然后将三段上、三段中、三段下分别混合洗匀为“上、中、下”三堆图片,从这三堆图片中各随机抽取一张,则恰好能组成一张完整风景图片的概率是( )
A. B. C. D.
32.桌上倒扣着背面相同的5张扑克牌,其中3张黑桃、2张红桃.从中随机抽取一张,则( )
A.能够事先确定抽取的扑克牌的花色 B.抽到黑桃的可能性更大
C.抽到黑桃和抽到红桃的可能性一样大 D.抽到红桃的可能性更大
二、填空题
33.某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 50 100 200 500 1000
“射中9环以上”的次数 15 41 78 158 405 801
“射中9环以上”的频率
根据频率的稳定性,估计这名运动员射击一次“命中9环以上”的概率为 .
34.为了估计鱼塘中鱼的数量,养鱼者首先从鱼塘中打捞100条鱼,在每一条鱼身上做好记号后把这些鱼放归鱼塘,一段时间后再从鱼塘中打捞 50 条鱼.如果在这些鱼中有10条鱼是有记号的,那么估计鱼塘中鱼的条数为 .
35.三辆汽车经过丁字路口,可能向左转,也可能向右转,如果这两种可能性大小相同,那么这三辆汽车都朝一个方向转的概率是 .
36.某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中8环以上”的次数 18 68 82 168 327 823
“射中8环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中8环以上”的概率约是 .
37.某篮球运动员在罚球线上投篮的结果如下表所示:
投篮次数 50 100 150 200 250 300 500
投中次数m 28 60 78 104 123 152 251
投中频率 0.56 0.60 0.52 0.52 0.49 0.51 0.50
那么估计这名篮球运动员投篮一次投中的概率是 (结果精确到0.01).
38.某数学兴趣小组做“任意拋掷一枚图钉”的重复试验,多次试验后获得如下数据:
重复试验次数 10 50 100 500 1000
钉尖朝上次数 5 15 36 200 400
由此可以估计任意拋掷一次图钉,钉尖朝上的概率约为 .(结果精确到0.1)
39.小明在操场上做游戏,他在沙地上画了一个面积为的矩形,并在四个角画上面积不等的扇形,在不远处的固定位置向矩形内部投石子,记录如下(石子不会落在矩形外和各区域边缘):
投石子的总次数 50次 150次 300次 600次
石子落在空白区域内的次数 14次 85次 199次 400次
石子落在空白区域内的频率
依此估计空白部分的面积可能是 .
40.下图是由9个小正方形组成的图案,从图中随机取一点,这点在阴影部分的概率是 .
41.如图,矩形中,,E为的中点,连接.以E为圆心,长为半径画弧,分别与交于点F,G.向该矩形游戏板随机发射一枚飞针,则击中图中阴影部分区域的概率为 .
42.在一个不透明的口袋中有红色、黄色和绿色球共60个,它们除颜色外,其余完全相同,在不倒出球的情况下,发现摸到红球和绿球的频率分别稳定在和,由此推测口袋中黄球的个数是 个.
43.从,0,,,3.2这五个数中,随机抽取一个,则抽到无理数的概率是 .
44.甲、乙、丙三位同学把自己的数学课本故在一起,每人从中随机抽取一本(不放回),三位同学抽到的课本都是自己课本的概率是 .
45.如果所示的地板由15块方砖组成,每一块方砖除颜色外完全相同,小球自由滚动停在黑砖的概率为 .
46.如图,是由7个全等的正六边形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是 .
47.一只自由飞行的小鸟,如果随意落在如图所示的方格地面上(每个小方格形状完全相同),那么小鸟落在阴影方格地面上的概率是 .
48.某路口的人行造交通信号灯每分钟红灯亮秒,绿灯亮秒,黄灯亮5秒,当小明到达该路口时,遇到红灯的概率是 .
49.如图是可以自由转动的三个转盘,请根据下列情形回答问题(不考虑指针落在分界线上).
(1)转盘1被分成了2个扇形,圆心角为的扇形涂成红色,其余部分涂成白色,转动转盘1,当转盘1停止转动时,指针落在红色区域的概率是 .
(2)转盘2、转盘3都已被分成了3个相同的扇形,并且分别涂成红色、白色、黄色,同时转动转盘2和转盘3,当两个转盘停止转动时,则指针落在区域的颜色都是红色的概率为 .
50.把一枚均匀的硬币连续抛掷两次,两次正面朝上的概率是 .
51.如图,一块飞镖游戏板由大小相等的小正方形格子构成.向游戏板随机投掷一枚飞镖(每次飞镖均落在纸板上),击中阴影区域的概率是 .
52.如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为 .
53.如图,是一个圆盘及其内接正六边形,随机往圆盘内投飞镖,则飞镖落在正六边形内的概率是 .
三、解答题
54.第19届亚运会于2023年9月23日至10月8日在杭州成功举行,现有三张印有亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片,除正面图案不同外,其余均相同.
(1)从中随机抽取一张卡片,则抽出的卡片图案是“莲莲”的概率是________;
(2)从中随机抽取一张卡片,放回后再抽取一张,请用画树形图或列表法求抽出的两张卡片都是“莲莲”的概率.
55.某班数学兴趣小组进行如下活动:组长从一副扑克牌中选取六张分给两位同学,小明分到的三张扑克牌分别是方块,,;小亮分到的是方块,,.两人将分到的牌随机放在桌上(数字一面朝下),然后各自从对方的牌中抽一张进行比较,抽牌数字较大的人当“小老师”,给全班同学讲一个关于数学家的故事.
(1)若小亮从对方的扑克牌中抽一张,则抽到方块的概率是______;
(2)用列表法或画树状图法中的一种方法,求小明能当“小老师”的概率.
56.学校为增加节日气氛,在新年来临之际举行一次抽奖活动;如图是一个可以自由转动、质地均匀的转盘,每位学生都有一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品.下表是活动进行中的一组统计数据:
转动转盘的次数
落在“铅笔”的次数
落在“铅笔”的频率
(1)直接写出转动该转盘一次,获得铅笔的概率(结果保留小数点后两位),并直接写出饮料所在扇形的圆周角的度数(结果精确到);
(2)小明同学设计了一个摸球试验,在口袋中放一个白球和若干个红球,从中随机摸出一球,如果是白球,就获得饮料,如果是红球,就获得铅笔.并且这个试验中获得铅笔的概率跟学校抽奖活动的结果是一样的.
直接写出红球的个数;
直接写出两次摸球都获得饮料的概率.
57.一个不透明的袋子里有4个小球,小球上各标有一个数字,分别是1,2,4,7.这些小球除标有的数字不同外其他都相同.
(1)从这个袋子里随机摸出一个小球,摸出标有数字“2”的小球的概率是________;
(2)先从袋中随机摸出一个小球,记下小球上的数字后,放回、摇匀,再从袋子中随机摸出一个小球,记下小球上的数字,第一次记下的数放在十位,第二次记下的数放在个位组成两位数,请运用画树状图或列表的方法,求这个两位数是偶数的概率.
58.有5张看上去无差别的卡片,上面分别写着1,2,3,4,5.
(1)随机抽取1张卡片,则取出的卡片上数字为偶数的概率为______.
(2)若一次性抽取两张卡片,请用画树状图法或列表法求两张卡片上的数字和为奇数的概率.
59.A盒中有2个黄球、1个红球,B盒中有1个黄球、1个红球,这些球除颜色外无其他差别.
(1)若从A盒中随机取出1个球,则取出的球是红球的概率是______;
(2)若分别从每个盒中随机取出1个球,请用列表或画树状图的方法求取出的两个球中恰好是1个黄球、1个红球的概率.
60.在不透明的袋子里装有2个红球、1个蓝球(除颜色外其余都相同).
(1)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表的方法,求两次摸到一红一蓝的概率.
(2)若向袋中再放入若干个同样的蓝球,搅拌均匀后,使从袋中摸出一个蓝球的概率为,求后来放入袋中的蓝球个数.
61.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.
(1)随机摸出一个小球,直接写出小球标号是偶数的概率;
(2)随机一次摸出两个小球,用画树状图或列表的方法,求两个小球标号之和是偶数的概率;
(3)随机摸出一个小球然后放回,再随机摸出一个小球,直接写出两个小球标号之和是偶数的概率.
62.在一个不透明的纸盒里装有红、白、黄三种颜色的乒乓球4个(除颜色外完全相同),其中白球2个,红球、黄球各1个.
(1)从纸盒中随机摸出一个球,事件“摸到白球”的概率是______;
(2)若摸到红球得1分,摸到白球得2分,摸到黄球得3分.小明随机从纸盒中一次摸出两个球,请用画树状图法或列表法求小明至多得4分的概率.
63.一个不透明的布袋中装有1个红球,1个黑球和若干个白球,它们除颜色外其余都相同.从中任意摸出1个球,是白球的概率为.
(1)直接写出布袋中白球的个数;
(2)从布袋中先摸出一个球后放回,再摸出一个球,请用列表或画树状图法求两次摸到的球都是白球的概率.
64.党的十八大以来,某市以习近平新时代中国特色社会主义思想为指导,全面贯彻习主席关于扶贫开发的重要论述,在省委、省政府的坚强领导下,历经十年,全市减贫任务基本完成,脱贫攻坚取得阶段性成果,为了进一步巩固该成果,该市市委决定从甲、乙、丙、丁四名优秀共产党员中随机选取2名党员,到该市刚脱贫的某村庄蹲点指导工作,力争用五年的时间让该村村民走上致富之路.
(1)事件“甲、戊两名共产党员被选取到”是________事件;
(2)请用树状图或列表法求出恰好选取到甲和乙两名优秀共产党员的概率.
65.小明学习物理《电流和电路》后设计如图所示的一个电路图,其中、、分别表示三个可开闭的开关,“”表示小灯泡,“”表示电池.
(1)当开关闭合时,再随机闭合开关或其中一个,直接写出小灯泡发光的概率;
(2)当随机闭合开关、、中的两个,试用树状图或列表法求小灯泡发光的概率.
66.甲、乙两个不透明的盒子里分别装有3张卡片,其中甲盒里3张卡片分别标有数字1,2,3;乙盒里3张卡片分别标有数字4,5,6,这些卡片除数字外都相同,将卡片充分摇匀.
(1)从甲盒里随机抽取一张卡片,抽到的卡片上的数字为偶数的概率是______;
(2)从甲盒、乙盒里各随机抽取一张卡片,请用列表或画树状图的方法,求抽到的两张卡片上的数字之和能被3整除的概率.
67.从甲、乙、丙、丁4名学生中选2名学生参加一次乒乓球单打比赛,求下列事件发生的概率.
(1)甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是 ;
(2)任意选取2名学生参加比赛,求一定有乙的概率.(用树状图或列表的方法求解).
68.一只不透明袋中装有1个白球和若干个红球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从袋中摸出1个球,记下颜色后放回、揽匀,不断重复这个过程,获得数据如下:
摸球的次数 200 300 400 1000 1600 2000
摸到白球的频数 72 93 130 334 532 667
摸到白球的频率 0.03600 0.03100 0.03250 0.03340 0.03325 0.03335
(1)该小组发现,摸到白球的频率在一个常数附近摆动,这个常数是______(精确到0.001),由此估出红球有______个;
(2)现从该袋中随机摸出一个球,不放回,再摸出一个球,请用画树状图或列表法求恰好摸到1个白球和1个红球的概率.
69.箱子里有3个红球和2个黄球,从箱子中一次拿出两个球出来.
(1)请你用列表或画树形图的方法,求一次拿出的两个球正好是一红一黄的概率;
(2)直接写出两个球都是红球的概率.
70.在5张相同的小纸条上,分别写有语句:①函数表达式为;②函数表达式为;③函数的图像关于原点对称;④函数的图像关于轴对称;⑤函数值随自变量增大而增大.将这5张小纸条做成5支签,①、②放在不透明的盒子中搅匀,③、④、⑤放在不透明的盒子中搅匀.
(1)从盒子中任意抽出1支签,抽到①的概率是______;
(2)先从盒子中任意抽出1支签,再从盒子中任意抽出1支签.求抽到的2张小纸条上的语句对函数的描述相符合的概率.
71.经过某十字路口的汽车可能直行也可能左转或者右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率.
(1)两辆车向左转,一辆向右转;
(2)至少有两辆车向右转.
72.一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.甲从口袋中随机摸取一个小球,记下标号m,然后放回,再由乙从口袋中随机摸取一个小球,记下标号n,组成一个数对(m,n).
(1)用列表法或画树状图法,写出(m,n)所有可能出现的结果;
(2)甲、乙两人玩游戏,规则如下:按上述要求,两人各摸取一个小球,小球上标号之和为奇数则甲赢,小球上标号之和为偶数则乙赢.你认为这个游戏规则公平吗?请说明理由.
73.不透明的袋子中装有红色小球1个、绿色小球2个,除颜色外无其它差别.
(1)从袋中随机摸出一个小球,直接写出摸到红球的概率;
(2)随机摸出一个小球,记下颜色,放回并摇匀,再随机摸出一个,求两次都摸到绿球的概率.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A A B B C B B B C
题号 11 12 13 14 15 16 17 18 19 20
答案 C A A D A A A B B D
题号 21 22 23 24 25 26 27 28 29 30
答案 C A D B A D D C C D
题号 31 32
答案 B B
1.B
【分析】本题考查了必然事件.熟记事件分类及相应概念是解决问题的关键.
根据必然事件的定义进行判断作答即可.
【详解】解:由题意知,从袋子中随机摸出3个球,
至少有1个是白球为随机事件,故A不符合要求;
至少有1个是红球为必然事件,故B符合要求;
至少有2个是红球为随机事件,故C不符合要求;
至少有2个是白球为随机事件,故D不符合要求;
故选:B.
2.A
【分析】本题考查事件的分类,根据一定条件下,可能发生,可能不发生的事件为随机事件,进行判断即可.
【详解】解:“翻开人教版《数学》九年级下册课本恰好翻到第56页”这个事件是随机事件;
故选A.
3.A
【分析】本题考查了必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
【详解】解:事件(1)是随机事件;事件(2)是随机事件;
故选A.
4.B
【分析】画出树状图,求得所有等可能的结果数,再得到只有一辆汽车向左转的结果数,然后利用概率公式求解即可;
【详解】解:根据题意,画出树状图,如图,
由图知,一共有27种等可能的结果,其中只有一辆汽车向左转的结果有12种,
∴只有一辆汽车向左转的概率为.
故选:B.
5.B
【分析】本题考查了随机事件,通过概率说明可能性大小,理解随机事件,掌握概率计算公式是解题的关键.
【详解】解:A.从中随机抽取1个球,抽到红球的概率为,抽到蓝球的概率为,结论正确,不符合题意;
B.从中随机抽取1个球,抽到红球的概率为,抽到蓝球的概率为,结论错误,符合题意;
C.因为只有个红球,所以从中随机抽取6个球,至少有个是蓝色的,结论正确,不符合题意;
D.从中随机抽取5个球,可能都是红色的,结论正确,不符合题意;
故选:B.
6.C
【分析】本题主要考查了用树状图求等可能事件的概率,方法是用树状图或列表法列举出所有可能出现的结果总数,找出符合条件的结果数,用分数表示即可,注意每种情况发生的可能性相等.先利用画树状图,得出所有可能出现的结果总数,从中找到符合条件的结果数,然后求出概率即可.
【详解】解:根据题意,画出树状图,如图,
由图知,一共有27种等可能的结果,其中至少有两辆车直行的结果有7种,
∴至少有两辆车直行的概率为.
故选:C.
7.B
【分析】此题考查了事件的分类,事件分为随机事件和确定事件,确定事件包含必然事件和不可能事件,据此进行判断即可.
【详解】解:“经过有交通信号灯的路口,遇到黄灯”这个事件是随机事件,
故选:B
8.B
【分析】本题主要考查了事件的分类,解题的关键是理解题意,弄清成语的含义.根据事件的分类进行解答即可.
【详解】解:A.旭日东升是必然事件,故A不符合题意;
B.心想事成是随机事件,故B符合题意;
C.水中捞月是不可能事件,故C不符合题意;
D.只手遮天是不可能事件,故D不符合题意.
故选:B.
9.B
【分析】本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出,再从中选出符合事件A或的结果数目,然后根据概率公式计算事件A或事件的概率.
先画树状图得出所有等可能结果数,从中找到“关联数”的结果数,再根据概率公式求解即可.
【详解】解:画树状图,
由图可知,所有可能组成的数有123、132、213、231、312、321,共有6种,其中恰好是“关联数”的有123、321,共 2种,
所以恰好是“关联数”的概率为,
故选:B.
10.C
【分析】本题主要考查随机事件的概念,它与必然事件,不可能事件相对.
解题的关键是熟练掌握各个概念“随机事件是可能发生也可能不发生的事件;必然事件就是一定发生的事件;不可能事件就是一定不发生的事件”;据此解答即可.
【详解】解:A,B,D都是不可能事件.
所以是随机事件的是守株待兔.
故选:C.
11.C
【分析】
画出树状图,再根据概率公式计算即可得;
本题主要考查画树状图或列表法求概率,得到所求的情况数是解决本题的关键.
【详解】画树状图如下:
由树状图可知共有8种等可能结果,其中恰有两次正面向上的有3种,
所以恰有两次正面向上的概率为,
故选:C.
12.A
【分析】根据随机事件的定义即可得出答案.
【详解】解:∵通常温度降到0℃以下,纯净的水会结冰,
∴这个事件是必然事件.
故选:A.
【点睛】本题考查的是必然事件,不可能事件,随机事件的概念.必然事件指在一定条件下, 一定发生的事件,不可能事件是指在一定条件下, 一定不发生的事件,不确定事件即随机事件是指在一定条件 下,可能发生也可能不发生的事件.
13.A
【分析】分别求出每个选项中的概率,和由频率统计图估计出的概率作比较即可得出答案
【详解】解:、选项中取到红球的概率是,、选项中出现点的概率是,、选项中出现正面的概率是,、选项中能被整除的概率即为偶数的概率为,
由图知,随着试验次数的增加,频率逐渐稳定在附近,所以符合条件的只有.
故选:.
【点睛】本题考查了频率估计概率,利用概率公式求概率,正确求出每项概率和由频率估计出的概率作比较是解答本题的关键.
14.D
【分析】根据题意列出表格,得出所有等可能的情况数,找出随机取出一把钥匙开任意一把锁,一次打开锁的情况数,即可求出所求的概率.
【详解】解:列表得:
锁1 锁2
钥匙1 (锁1,钥匙1) (锁2,钥匙1)
钥匙2 (锁1,钥匙2) (锁2,钥匙2)
钥匙3 (锁1,钥匙3) (锁2,钥匙3)
由表可知,所有等可能的情况有6种,其中随机取出一把钥匙开任意一把锁,一次打开锁的2种,
则P(一次打开锁).
故选D.
【点睛】本题考查列表法与树状图法求概率,掌握概率等于所求情况数与总情况数之比是解题的关键.
15.A
【分析】根据频数和频率的关系进行判断即可
【详解】A. 如果继续对这批羽毛球进行质量检验,优等品的频率将在0.94附近摆动,故此选项正确;
B. 从这批羽毛球中任意抽取一只,不一定是优等品,故此选项错误;
C. 从这批羽毛球中任意抽取50只,优等品有不一定为47只,故此选项错误;
D. 从这批羽毛球中任意抽取1100只,优等品的频率不一定在0.940~0.941的范围内,故此选项错误.
故选:A.
【点睛】本题主要考查利用频率估计概率的知识,熟练掌握利用频率估计概率的知识是解题的关键.
16.A
【分析】依据“随机事件:在一定条件下有可能发生也有可能不发生的事件”、“必然事件:在一定条件下一定会发生的事件”、“不可能事件:在一定条件下一定不会发生的事件”进行判断即可、“确定性事件:包括必然事件和不可能事件”进行判断即可.
【详解】解:“守株待兔”是随机事件,
故选:A.
【点睛】本题考查了随机事件、必然事件、不可能事件;熟记相关概念是解题的关键.
17.A
【分析】画树状图得出所有等可能的结果数,再从中找到符合条件的结果数,然后再用概率公式求解即可.
【详解】解:树状图如图所示,
一共有12种等可能性,其中王明选中的卡片中有偶数的可能性有10种可能性,
故王明选中的卡片中有偶数的概率为:,
故选:A.
【点睛】本题主要考查的是用列表法或树状图法求概率,列表法可以重复不遗漏的列出所有可能的结果,适合于两步完成的事件,树状图法适合两步或两步以上完成的事件,用到的知识点为:概率等于所求情况数与总情况数之比.
18.B
【分析】根据题意列出树状图求出各种颜色求得概率,逐个判断即可得到答案;
【详解】解:由题意可得,
摸出红球的概率为,摸出黄球的概率为:,摸出黑球的概率为:,
故选B;
【点睛】本题考查概率定义及树状图法求概率,解题的关键是正确理解概率的定义.
19.B
【分析】依据题意先用画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率.
【详解】解:由题意,画树状图得∶
∴一共有12种情况,第一节上数学课,第四节上语文课只有1种情况,
∴第一节上数学课,第四节上语文课的概率为 .
故选B.
【点睛】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏地列出所有可能的结果,适合于两步完成的事件.用到的知识点为∶概率=所求情况数与总情况数之比.
20.D
【分析】根据白球两个,摸出三个球必然有一个黑球.
【详解】解:A袋子中装有4个黑球和2个白球,摸出的三个球中可能为两个白球一个黑球,所以A不是必然事件;
B.C.袋子中有4个黑球,有可能摸到的全部是黑球,B、C有可能不发生,所以B、C不是必然事件;
D.白球只有两个,如果摸到三个球不可能都是白梂,因此至少有一个是黑球,D正确.
故选D.
【点睛】本题考查随机事件,解题关键在于根据题意对选项进行判断即可.
21.C
【分析】本题主要考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.熟知这三类事件的区别是解题的关键.
根据这三类事件的定义,逐项判断即可求解.
【详解】解:A.打开电视机,正在直播足球比赛是随机事件,故本选项不符合题意;
B.在只装有2个玻球的袋中摸出一个球是黑球是随机事件,故本选项不符合题意;
C.掷一次骰子,向上的一面出现的点数大于7是不可能事件,故本选项符合题意;
D.当室外温度低于时,一碗清水在室外会结冰是必然事件,故本选项不符合题意;
故选:C.
22.A
【分析】根据树形图,可得此次摸球的游戏规则是:随机摸出一个球后放回,再随机摸出1个球
【详解】解:观察树状图可得:袋子中共有红、黄、蓝三个小球,此次摸球的游戏规则是随机摸出一个球后放回,再随机摸出1个球,
故选:A.
【点睛】此题考查列表法与树状图法求概率,解题关键在于利用树状图进行解答.
23.D
【分析】根据随机事件和必然事件的概念判断可得.
【详解】解:事件①:任意画一个多边形,其外角和为360°,这是必然事件;
事件②:经过一个有交通信号灯的十字路口,遇到红灯,这是随机事件;
故选:D.
【点睛】本题考查的是理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
24.B
【详解】解:画树状图得:
∵共有9种等可能的结果,小明和小亮选到同一社区参加实践活动的有3种情况,
∴小明和小亮选到同一社区参加实践活动的概率为:
故选B
25.A
【分析】首先根据题意画出树状图,由树状图求得所有等可能的结果与第一次摸到红球,第二次摸到绿球的情况,然后利用概率公式求解即可求得答案.
【详解】解:画树状图得:
∵共有4种等可能的结果,第一次摸到红球,第二次摸到绿球有1种情况,
∴第一次摸到红球,第二次摸到绿球的概率为,
故选:A.
【点睛】本题考查了画树状法或列表法求概率,列出所有等可能的结果是解决本题的关键.
26.D
【分析】直接根据随机事件的概念即可得出结论.
【详解】购买一张彩票,结果可能为中奖,也可能为不中奖,中奖与否是随机的,即这个事件为随机事件.
故选:D.
【点睛】本题考查了随机事件的概念,解题的关键是熟练掌握随机事件发生的条件,能够灵活作出判断.
27.D
【分析】列树状图或画表格得到所有可能情况,然后找出第二次取出的球的号码不小于第一次取出的球的号码的情况,计算概率即可.
【详解】解:列树状图为:
由上图可知共16种等可能情况,符合要求的共有10种结果,
故第二次取出的球的号码不小于第一次取出的球的号码的概率为.
故选D.
【点睛】本题考查概率公式,解题的关键是能用树状图或列表法表示所有等可能情况.
28.C
【分析】必然事件: 在一定条件下,一定会发生的事件,叫做必然事件,随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件;根据概念判断即可.
【详解】(1)通常温度降到以下,纯净的水结冰,是必然事件;
(2)随意翻到一本书的某页,页码是奇数,是随机事件;
(3)明天太阳从东方升起,是必然事件;
(4)购买1张彩票,中奖,是随机事件;
故选:C.
【点睛】本题考查的是随机事件与必然事件的含义,掌握“利用概念判断随机事件与必然事件”是解本题的关键.
29.C
【分析】根据随机掷一枚质地均匀的硬币三次,可以分别假设出三次情况,画出树状图即可.
【详解】解:列树状图如下所示:
根据树状图可知一共有8种等可能性的结果数,恰好有两次正面朝上的事件次数为:3,
∴恰好有两次正面朝上的事件概率是:.
故选C.
【点睛】本题主要考查了树状图法求概率,解题的关键是根据题意画出树状图.
30.D
【分析】必然事件: 在一定条件下,一定会发生的事件,叫做必然事件,随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件;根据概念判断即可.
【详解】解:事件(1):购买1张福利彩票,中奖,是随机事件,
事件(2):掷一枚六个面的点数分别为1,2,3,4,5,6的骰子,向上一面的点数不大于6,是必然事件,
故选D
【点睛】本题考查的是随机事件与必然事件的含义,掌握“利用概念判断随机事件与必然事件”是解本题的关键.
31.B
【分析】把三张风景图片用甲、乙、丙来表示,根据题意,画出树状图,得出可能出现的结果及满足条件的结果,利用概率公式求解即可得.
【详解】解:把三张风景图片用甲、乙、丙来表示,根据题意,画出如下树状图:
从树状图可得:所有可能出现的结果共有27种,这些结果出现的可能性相同,其中恰好组成一张完整风景图片的可能有3种,
∴三张图片恰好组成一张完整风景图片的概率为:,
故选:B.
【点睛】题目主要考查列表法或树状图法求概率,理解题意,熟练掌握运用列表法或树状图法是解题关键.
32.B
【分析】要求可能性的大小,只需求出各自所占的比例大小即可.求比例时,应注意记清各自的数目.
【详解】解:A、因为袋中扑克牌的花色不同,所以无法确定抽取的扑克牌的花色,故本选项错误;
B、因为黑桃的数量最多,所以抽到黑桃的可能性更大,故本选项正确;
C、因为黑桃和红桃的数量不同,所以抽到黑桃和抽到红桃的可能性不一样大,故本选项错误;
D、因为红桃的数量小于黑桃,所以抽到红桃的可能性小,故本选项错误.
故选B.
33./
【分析】本题考查了利用频率估计概率,解决本题的关键是理解当试验的所有可能结果不是有限个或结果个数很多,或各种可能结果发生的可能性不相等时,一般通过统计频率来估计概率.大量重复试验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
【详解】解:根据表格数据可知:
根据频率稳定在,估计这名运动员射击一次时“射中9环以上”的概率是.
故答案为:.
34.500条
【分析】本题考查了用样本估计总体;设鱼塘中鱼的条数为x条,根据题意得,求解即可.
【详解】解:设鱼塘中鱼的条数为x条,
根据题意得:,
解得:.
故答案为:500条.
35.
【分析】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式计算事件或事件的概率.
画树状图展示所有种等可能的结果数,再找出三辆汽车都朝一个方向转的结果数,然后根据概率公式求解即可.
【详解】画树状图为:
共有种等可能的结果数,其中三辆汽车都朝一个方向转的结果数为,
所以至少有两辆车向右转的概率为,
故答案为:.
36.
【分析】本题考查用频率估计概率,根据大量的实验结果稳定在,即可得出结论.
【详解】解:由题知,射击次数越多,“射中8环以上”的频率越接近,
所以这名运动员射击一次时“射中8环以上”的概率约是.
故答案为:.
37.0.50
【分析】根据频率估计概率的方法,结合表格数据即可得出答案.
【详解】解:由频率分布表可知,随着投篮次数越来越大,频率逐渐稳定到常数附近,
则估计这名球员在罚球线上投篮一次投中的概率为,
故答案为:.
【点睛】本题考查了利用频率估计概率,解题的关键是理解这种概率的得出是在大量实验的基础上得出的,不能单纯的依靠几次决定.
38.0.4
【分析】此题主要考查了利用频率估计概率,首先通过实验得到事件的频率,然后用频率估计概率即可解决问题.观察表格的数据求出每次试验得到的频率可以得到图钉钉尖朝上的频率,然后用频率估计概率即可求解.
【详解】解:表中图钉钉尖朝上的频率分别为,,,,
图钉钉尖朝上频率逐渐稳定在0.40左右,
估计任意抛掷一枚图钉,图钉钉尖朝上的概率约为0.4.
故答案为:0.4
39.4
【分析】本题主要是利用频率估计概率、概率的应用等知识点,掌握当实验次数越多时,某事件的频率越接近于该事件的概率是解题的关键.
根据投在空白区域内的频率得到概率的大小,由此计算空白区域的面积即可.
【详解】解:由表格可知:
当投石子的次数越来越多时,石子落在空白区域的频率越接近,即空白区域的面积占总面积的,
∴空白部分的面积=.
故选答案为4.
40.
【分析】直接根据几何概率求解即可.
【详解】解:图中共有9个小正方形,其中阴影部分共有5个小正方形,
∴从图中随机取一点,这点在阴影部分的概率是,
故答案为:.
【点睛】本题考查几何概率求解,理解并掌握几何概率是解题关键.
41.
【分析】本题考查了矩形的性质和不规则面积的计算,利用矩形的性质求得,进而可得,然后根据解答即可.熟练掌握矩形的性质、明确阴影面积为两个全等的等腰直角三角形的面积减去两个圆心角为的扇形面积是解题关键.
【详解】解:∵四边形是矩形,,,E为的中点,
,,
,
,
∴击中图中阴影部分区域的概率为;
故答案为:.
42.24
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,用频率估计概率可知黄色球的数量为总数乘以其所占百分比.
【详解】解:根据题意得:
(个),
答:此推测口袋中黄球的个数是24个.
故答案为:24.
【点睛】本题主要考查频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
43.
【分析】利用简单的概率公式计算即可.
【详解】∵一共有5种等可能性,无理数有,共2种等可能性,
∴抽到无理数的概率是.
故答案为:.
【点睛】本题考查了简单的概率公式求概率,熟练掌握公式是解题的关键.
44.
【分析】画出树状图,根据树状图即可得出答案.
【详解】设甲的数学课本用表示,乙的数学课本用表示,丙的数学课本用表示,画树状图如下:
由树状图可知,共有六种等可能的结果数,其中三位同学抽到的课本都是自己的课本有一种结果,所以三位同学抽到的课本是自己课本的概率是.
【点睛】本题主要考查概率的计算,熟练掌握概率的计算方法是解决本题的关键.
45.
【分析】本题考查了几何概率,把黑色方砖的面积除以总面积,即可作答.
【详解】解:∵总面积为15块方砖的面积,且每个其中方砖的面积是相等的,黑色方砖有5块,
∴小球停在黑色方砖的概率为,
故答案为:
46.
【分析】根据阴影部分的面积所占比例得出概率即可.
【详解】解:由图知,阴影部分的面积占图案面积的,即这个点取在阴影部分的概率是,
故答案为:.
【点睛】本题考查几何概率.熟练掌握几何概率的计算方法,是解题的关键.
47.
【详解】∵由题意和图可知,阴影部分的面积占整个方格地面的比值为:,
∴小鸟落在阴影方格地面上的概率为:.
48.
【分析】本题考查了概率,根据题意和概率公式即可得,掌握概率公式是解题的关键.
【详解】解:∵每分钟红灯亮秒,绿灯亮秒,黄灯亮5秒,
∴当小明到达该路口时,遇到红灯的概率:,
故答案为:.
49.
【分析】本题考查几何概率、用列表法或树状图法求概率,熟知求几何概率可利用长度比、面积比、体积比等.
(1)用红色区域的面积除以圆面积可求解;
(2)用列表法得到所有的等可能的结果,进而得到符合条件的结果数,利用求概率公式即可.
【详解】解:(1)根据题意,当转盘1停止转动时,指针落在红色区域的概率是,
故答案为:;
(2)列表为
红 白 黄
红 红红 白红 黄红
白 红白 白白 黄白
黄 红黄 白黄 黄黄
由表知,共有9种等可能的结果,其中指针落在区域的颜色都是红色的有1种,
∴指针落在区域的颜色都是红色的概率为,
故答案为:.
50.
【分析】举出所有情况,看正面都朝上的情况数占总情况数的多少即可.
【详解】解:共4种情况,正面都朝上的情况数有1种,所以概率是.
故答案为:.
考点:列表法与树状图法.
51.
【分析】根据几何概率的求解公式即可求解.
【详解】解:设图中每个小正方形的面积为1,则大正方形的面积为9,
根据题意图中阴影部分的面积为3,
则P(击中阴影区域).
故答案为:.
【点睛】此题主要考查概率的求解,解题的关键是熟知几何概率的公式.
52.
【分析】用正方形的内切圆的面积的一半除以正方形的面积得到针尖落在黑色区域内的概率.
【详解】解:设正方形的边长为,
∵黑色区域面积为正方形的内切圆的面积的一半,
∴针尖落在黑色区域内的概率.
故答案为:.
【点睛】本题考查了几何概率:某事件的概率某事件所占有的面积与总面积之比.
53.
【分析】设圆的半径为,先分别求出圆的面积和正六边形的面积,再利用概率公式即可得.
【详解】解:如图,设圆的圆心为点,半径为,过点作于点,连接,
则圆的面积为,,
图中的六边形是正六边形,
,
是等边三角形,
,
正六边形的面积为,
则飞镖落在正六边形内的概率是,
故答案为:.
【点睛】本题考查了求概率、圆与正六边形等知识点,熟练掌握概率的求法是解题关键.
54.(1)
(2)
【分析】
本题考查列表法与树状图法、概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
(1)直接利用概率公式可得答案.
(2)画树状图得出所有等可能的结果数以及两次抽到的卡片都是“莲莲”的结果数,再利用概率公式可得出答案.
【详解】(1)解:由题意得,从这三张卡片中随机抽取一张,图案恰好是“莲莲”的概率为.
故答案为:;
(2)解:将琮琮、宸宸和莲莲的不透明卡片分别记为A,B,C,
画树状图如下:
共有9种等可能的结果,其中两次抽到图案都是“莲莲”的结果有1种,
∴两次抽到图案都是“莲莲”的概率为.
55.(1)
(2)
【分析】(1)共三张,每一张被抽到的概率都是相等的;
(2)列出表格,根据要求计算相应结果数量与总数量的比值即可.
【详解】(1)解:抽到方块的概率是,
故答案为:;
(2)解; 根据题意列表如下:
小明 小亮
由表可以看出,所有可能出现的结果共有种,这些结果出现的可能性相等.
其中小明取出的牌比小亮大的结果有,,共种.
(小明能当小老师).
【点睛】本题考查了简单的概率计算,掌握列表法或画树状图法是解题关键.
56.(1),;
(2) 个; .
【分析】()根据图表中的频率去估计概率及用即可;
()利用概率公式,摸到白球的概率为,摸到红球的概率为即可求解;
画树状图,然后利用概率公式求解;
本题考查了利用频率估计概率和列表法与树状图法求概率,解题的关键是灵活运用知识点的应用.
【详解】(1)根据表格可知:转动该转盘一次,获得铅笔的概率为,
饮料所在扇形的圆周角的度数;
(2)设红球的个数有个,
由()得,铅笔的概率为,
,解得:,
经检验:是分式方程的解,
∴红球的个数有个;
列表如下:
白 红 红 红
白 白、白 红、白 红、白 红、白
红 白、红 红、红 红、红 红、红
红 白、红 红、红 红、红 红、红
红 白、红 红、红 红、红 红、红
共有种等可能的结果数,其中两人都获得“饮料”的结果数为,
∴两人都获得“饮料”的概率为.
57.(1)
(2)
【分析】本题考查列表法与树状图法、概率公式,解答本题的关键是明确题意,画出相应的树状图,求出相应的概率.
(1)直接运用概率公式计算即可;
(2)根据题意可以画出相应的树状图,然后即可求出这个两位数是偶数的概率.
【详解】(1)解:由题意可得,
从袋中机摸出一个小球,则摸出标有数字“2”的小球的概率是.
(2)解:画树状图如下
由树状图可知一共有16种可能,且每种结果出现的可能性相同,其中这个两位数是偶数的结果数有8种,
这个两位数是偶数的概率为.
58.(1)
(2)
【分析】本题考查简单概率计算,利用列表法和树状图法计算概率.
(1)根据题意列式计算即可;
(2)根据题意列表列出等可能性即可得到本题答案.
【详解】(1)解:∵有5张看上去无差别的卡片,上面分别写着1,2,3,4,5,
∴偶数卡片为,
∴设取出的卡片上数字为偶数的结果为事件A.
∴;
(2)解:根据题意列表如下:
,
由上表可知,一次性抽取两张卡片,有20种等可能的结果,其中“两张卡片上数字和为奇数”的结果有12种.
∴P(两张卡片上数字和为奇数).
59.(1)
(2)树状图见解析,概率是
【分析】本题考查了概率的应用,掌握概率的计算公式以及树状图或列表法是解题关键.
(1)根据题意即可求解;
(2)画出树状图,确定可能出现的所有结果以及满足条件的结果数,即可求解.
【详解】(1)解:若从A盒中随机取出1个球,则取出的球是红球的概率是:;
故答案为:
(2)解:画树状图:
由树状图得共有6种等可能结果,其中取出的两个球中恰好1个黄球、1个红球的有3种结果,
(1黄1红).
60.(1) ;(2)9个
【分析】(1)根据题意画出树状图后,数出可能的结果总数及两次摸到不同颜色球的结果数,再根据概率的意义可得解;
(2)设放入x个蓝球,再根据概率的意义得到方程,解方程后可以得解.
【详解】解:(1)如图所示,
共有6种可能结果,每种结果发生的可能性相等;
其中两次摸到不同颜色球包含其中4种结果,
所以两次摸到不同颜色球的概率为;
(2)设放入x个蓝球,
由题意,得: ,
解得: x=9,
经检验, x=9 是原方程的解,
所以,放入袋中的蓝球为9个.
【点睛】本题考查概率的应用,熟练掌握概率的意义、树状图求概率的方法及方程思想方法的应用是解题关键.
61.(1)
(2)
(3)
【分析】本题考查列表法与树状图法、概率公式.
(1)直接利用概率公式可得答案.
(2)列表可得出所有等可能的结果数以及两个小球标号之和是偶数的结果数,再利用概率公式可得出答案.
(2)列表可得出所有等可能的结果数以及两个小球标号之和是偶数的结果数,再利用概率公式可得出答案.
【详解】(1)解:1,2,3,4中为偶数的是2和4,
∴随机摸出一个小球,标号是偶数的概率为.
(2)解:列表如下:
1 2 3 4
1
2
3
4
由表格可知,共有12种等可能的结果,其中两个小球标号之和是偶数的结果有:,,共4种,
∴两个小球标号之和是偶数的概率为.
(3)解:列表如下:
1 2 3 4
1
2
3
4
由表格可知,共有16种等可能的结果,其中两个小球标号之和是偶数的结果有:,,共8种,
∴两个小球标号之和是偶数的概率为.
62.(1)
(2)
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有12种等可能的结果,其中小明至多得4分的结果有8种,再由概率公式求解即可.
【详解】(1)解:由题意,共4种等可能结果,其中符合题意的结果有2种,
∴事件“摸到白球”的概率是,
故答案为:;
(2)画树状图如下:
共有12种等可能的结果,其中小明至多得4分的结果有8种,
∴小明至多得4分的概率为.
【点睛】本题考查的是树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
63.(1)2个
(2)
【分析】(1)设布袋中白球的个数为x个,根据概率公式列出方程,即可求解;
(2)根据题意,画出树状图,可得一共有16种等可能情况,其中两次都摸到白球的有4次,再根据概率公式计算,即可求解.
【详解】(1)解:设布袋中白球的个数为x个,根据题意得:
,
解得:.
经检验:是原方程的解,且符合题意,
即布袋中白球的个数为2个;
(2)解:根据题意,画出树状图,如下:
一共有16种等可能情况,其中两次都摸到白球的有4次,
∴ 两次摸到的球都是白球的概率为.
【点睛】本题考查列表法或树状图法求概率,熟练掌握概率公式是解题关键.
64.(1)随机
(2)
【分析】(1)甲、戊两名共产党员可能被选取到,也可能不被选取到,因此事件“甲、戊两名共产党员被选取到”是随机事件.
(2)先列表格或画树状图求出恰好选取到甲和乙两名优秀共产党员的所有可能结果,再代入概率的计算公式计算即可.
【详解】(1)事件“甲、戊两名共产党员被选取到”是随机事件,
故答案为:随机
(2)列表格如下
甲 乙 丙 丁
甲 甲乙 甲丙 甲丁
乙 乙甲 乙丙 乙丁
丙 丙甲 丙乙 丙丁
丁 丁甲 丁乙 丁丙
一共有12中结果,其中恰好选取到甲和乙的有两种结果,
∴恰好选取到甲和乙的概率=.
【点睛】本题主要考查了事件的分类及概率的计算,熟练掌握表格法和树状图法求事件发生的概率是解题的关键.
65.(1)
(2)
【分析】(1)根据电路图可知,当开关闭合时,想要小灯泡发光,只有闭合,从而可得出随机闭合开关或其中一个,小灯泡发光的概率;
(2)用树状图或列表法列出所有的情况,再找出能让小灯泡发光的情况,利用概率公式求解即可.
【详解】(1)解:当开关闭合时,想要小灯泡发光,只有闭合,
随机闭合开关或其中一个,小灯泡发光的概率为;
(2)法一:画出树状图如下:
共有6种等可能结果,其中能使小灯泡发光的组合共有4种,故(小灯泡发光).
法二:
列表如下:
(,) (,)
(,) (,)
(,) (,)
共有6种等可能结果,其中能使小灯泡发光的组合共有4种,故P(小灯泡发光).
【点睛】本题考查了用树状图或列表法求概率,解题的关键是结合物理知识,知道必须闭合,且闭合或中一个,小灯泡才会发光.
66.(1)
(2)
【分析】(1)由概率公式即可得出结果;
(2)画出树状图,由树状图求得所有等可能的结果与抽到的两张卡片上标有的数字之和能被3整除的结果,再由概率公式即可求得答案.
本题考查了树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
【详解】(1)解:从甲盒里随机抽取一张卡片,抽到的卡片上标有数字为偶数的概率是,
故答案为:;
(2)解:画树状图如下:
共有9种等可能的结果,其中两张卡片的数字之和能被3整除的结果有3种,
抽到的两张卡片上标有数字之和能被3整除的概率为.
67.(1)
(2)
【分析】(1)利用例举法例举所有的等可能的情况数,再利用概率公式进行计算即可;
(2)先列表得到所有的等可能的情况数以及符合条件的情况数,再利用概率公式进行计算即可.
【详解】(1)解:由甲一定参加比赛,再从其余3名学生中任意选取1名,共有甲、乙,甲、丙,甲、丁三种等可能,符合条件的情况数有1种,
∴甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是
(2)列表如下:
甲 乙 丙 丁
甲 甲、乙 甲、丙 甲、丁
乙 乙、甲 乙、丙 乙、丁
丙 丙、甲 丙、乙 丙、丁
丁 丁、甲 丁、乙 丁、丙
所有所有的等可能的情况数有12种,符合条件的情况数有6种,
所以一定有乙的概率为:
【点睛】本题考查的是利用例举法,列表的方法求解简单随机事件的概率,概率公式的应用,掌握“例举法与列表法求解概率”是解本题的关键.
68.(1)0.033,2
(2)
【分析】本题考查用频率估计概率、列表法或树状图法求概率,正确得到所有的等可能的结果是解答的关键.
(1)通过大量的实验,摸到白球的频率在一个常数附近摆动,这个常数可作为摸到白球的概率,进而可求解;
(2)利用列表法得到所有的等可能结果,再找出符合条件的结果数,然后利用求概率公式求解即可.
【详解】(1)解:由表可知,摸到白球的频率在一个常数附近摆动,这个常数为0.033,由此估出红球有
个,
故答案为:0.033,2;
(2)解:列表为:
白 红 红
白 红白 红白
红 白红 红红
红 白红 红红
由表知,共有6种等可能的结果,其中恰好摸到1个白球和1个红球的有4种,故恰好摸到1个白球和1个红球的概率为.
69.(1);
(2).
【分析】(1)根据题意画出树状图,求出所有可能数和符合条件数,运功概率公式求解即可;
(2)结合树状图,求出所有可能数和符合条件数,运功概率公式求解即可.
【详解】(1)解:画树状图:
由树状图可知,从箱子中一次拿出两个球共有种可能,
两个球正好是一红一黄的可能有种,
所以一次拿出的两个球正好是一红一黄的概率为:
答:一次拿出的两个球正好是一红一黄的概率为.
(2)由树状图可知,从箱子中一次拿出两个球共有种可能,
两个球都是红球的可能有6种,
所以两个球都是红球的概率为:
故答案为:.
【点睛】本题考查了无放回的随机抽样的概率求解;正确画出树状图、结合题意分析出符合条件的可能数是解题的关键.
70.(1)
(2)
【分析】(1)直接由概率公式求解即可;
(2)画出树状图,再由概率计算公式求解即可.
【详解】(1)解:从盒子中任意抽出1支签,抽到①的概率是;
故答案为:;
(2)解:画出树状图:
共有6种结果,抽到的2张小纸条上的语句对函数的描述相符合的有①、③和①、⑤和②、④共3种,
抽到的2张小纸条上的语句对函数的描述相符合的概率为.
【点睛】本题主要考查了列表法或树状图求概率,一次函数与二次函数的性质,解题的关键是会列出表或树状图以及一次函数与二次函数的性质.
71.(1)
(2)
【分析】(1)画出树状图,求得所有等可能的结果数,再得到两辆车向左转,一辆向右转的结果数,然后利用概率公式求解即可;
(2)根据树状图,得到至少有两辆车向右转的结果数,然后利用概率公式求解即可.
【详解】(1)解:画树状图,如图:
由图知,一共有27种等可能的结果,其中两辆车向左转,一辆向右转的结果有3种,
∴两辆车向左转,一辆向右转的概率为;
(2)解:由图知,至少有两辆车向右转的结果有7种,
∴至少有两辆车向右转的概率为.
【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.解题的关键是根据题意画出树状图,再由概率=所求情况数与总情况数之比求解.
72.(1)见解析;(2)这个游戏不公平,理由见解析
【分析】(1)根据题意画出树状图进行求解即可;
(2)根据(1)所画树状图,先得到所有的等可能性的结果数,然后分别得到小球标号之和为奇数和偶数的结果数,最后分别求出甲乙两人赢的概率即可得到答案.
【详解】解:(1)列树状图如下所示:
由树状图可知(m,n)所有可能出现的结果为:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3);
(2)由(1)得一共有9种等可能性的结果数,其中小球上标号之和为奇数的结果数有(1,2),(2,1),(2,3),(3,2),4种等可能性的结果数,其中小球上标号之和为偶数的结果数有(1,1),(1,3),(2,2),(3,1),(3,3),5种等可能性的结果数,
∴甲赢的概率为,乙赢的概率为,
∴这个游戏不公平.
【点睛】本题主要考查了画树状图和游戏的公平性,解题的关键在于能够熟练掌握画树状图的方法.
73.(1)
(2)
【分析】(1)由题意知,摸到红球的概率为;
(2)由题意画树状图,根据树状图求解即可.
【详解】(1)解:由题意知,摸到红球的概率为
∴摸到红球的概率为.
(2)解:由题意画树状图为:
由图可知,两次摸到绿球的概率为
∴两次摸到绿球的概率为.
【点睛】本题考查了树状图求概率.解题的关键在画出于正确的树状图.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题十二 概率相关概念及必考题型过关
一、单选题
1.在一个不透明的袋子中装有除颜色外无其他差别的3个红球,2个白球,从袋子中随机摸出3个球,下列事件为必然事件的是( ).
A.至少有1个是白球 B.至少有1个是红球
C.至少有2个是红球 D.至少有2个是白球
2.“翻开人教版《数学》九年级下册课本恰好翻到第56页”这个事件是( )
A.随机事件 B.必然事件 C.不可能事件 D.无法确定
3.有两个事件,事件(1):随意翻到一本书的某页,这页的页码是奇数;事件(2):射击运动员射击一次,命中靶心.下列判断正确的是( )
A.(1)(2)都是随机事件 B.(1)(2)都是必然事件
C.(1)是必然事件,(2)是随机事件 D.(1)是随机事件,(2)是必然事件
4.经过某十字路口的汽车可能直行也可能左转或者右转.如果这三种可能性大小相同,当三辆汽车经过这个十字路口时,只有一辆汽车向左转的概率是( )
A. B. C. D.
5.不透明的袋子里装有8个小球,其中5个红色,3个蓝色,则下列说法不正确的是( )
A.从中随机抽取1个球,抽到红色的可能性更大
B.从中随机抽取1个球,抽到红色和蓝色的可能性一样大
C.从中随机抽取6个球,一定有蓝色的
D.从中随机抽取5个球,可能都是红色的
6.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,则三辆汽车经过这个十字路口时,至少有两辆车直行的概率为( )
A. B. C. D.
7.“经过有交通信号灯的路口,遇到黄灯”这个事件是( )
A.确定性事件 B.随机事件 C.不可能事件 D.必然事件
8.下列描述的事件中,是随机事件的为( )
A.旭日东升 B.心想事成 C.水中捞月 D.只手遮天
9.如果一个三位数中任意两个相邻数字之差的绝对值不超过1,则称该三位数为“关联数”.用1,2,3这三个数字随机组成一个无重复数字的三位数,恰好是“关联数”的概率( )
A. B. C. D.
10.下列词语所描述的事件属于随机事件的是( )
A.拔苗助长 B.刻舟求剑 C.守株待兔 D.竹篮打水
11.同时抛掷三枚质地均匀的硬币,恰有两枚硬币反面向上的概率是( )
A. B. C. D.
12.通常温度降到0℃以下,纯净的水结冰.这个事件是( )
A.必然事件 B.不可能事件 C.随机事件 D.确定性事件
13.甲、乙两名同学在一次用频率去估计概率的试验中统计了某一结果出现的频率,绘出的统计图如图所示,则符合这一结果的试验可能是( )
A.从一个装有个白球和个红球的袋子中任取一球,取到红球
B.掷一枚正六面体的骰子,出现点
C.抛一枚硬币,出现正面
D.任意写一个整数,它能被整除
14.有两把不同的锁和三把钥匙,其中两把钥匙分别能打开这两把锁,第三把钥匙不能打开这两把锁,随机取出一把钥匙开任意一把锁,一次打开锁的概率是( )
A. B. C. D.
15.某批羽毛球的质量检验结果如下:
抽取的羽毛球数a 100 200 400 600 800 1000 1200
优等品的频数b 93 192 380 561 752 941 1128
优等品的频率 0.930 0.960 0.950 0.935 0.940 0.941 0.940
小明估计,从这批羽毛球中任意抽取的一只羽毛球是优等品的概率是0.94.下列说法中,正确的是( )
A.如果继续对这批羽毛球进行质量检验,优等品的频率将在0.94附近摆动
B.从这批羽毛球中任意抽取一只,一定是优等品
C.从这批羽毛球中任意抽取50只,优等品有47只
D.从这批羽毛球中任意抽取1100只,优等品的频率在0.940~0.941的范围内
16.“守株待兔”这个事件是( )
A.随机事件 B.确定性事件 C.必然事件 D.不可能事件
17.四张背面完全相同的卡片上分别写有1、2、3、4四个数字,把卡片背面朝上洗匀后,王明从这四张卡片中随机选两张,则王明选中的卡片中有偶数的概率是( )
A. B. C. D.
18.盒子里有个球,它们只有颜色不同,其中红球有6个,黄球有3个,黑球有1个.小军从中任意摸一个球,下面说法正确的是( )
A.一定是红球 B.摸出红球的可能性最大
C.不可能是黑球 D.摸出黄球的可能性最小
19.星期一上午班级共有4节课,分别为数学、语文、外语和历史,如果随机排课,那么第一节上数学课,第四节上语文课的概率为( )
A. B. C. D.
20.不透明袋子中有除颜色外完全相同的4个黑球和2个白球,从袋子中随机摸出3个球,下列事件是必然事件的是( ).
A.3个都是黑球 B.2个黑球1个白球
C.2个白球1个黑球 D.至少有1个黑球
21.下列事件中、属于不可能事件的是( )
A.打开电视机、正在直接足球比赛 B.在只装有2个玻璃球球的袋中摸出一个球是黑球
C.掷一次骰子,向上的一面出现的点数大于7 D.当室外温度低于时,一碗清水在室外会结冰
22.有一个从不透明的袋子中摸球的游戏,这些球除颜色外都相同,小红根据游戏规则,作出了如图所示的树状图,则此次摸球的游戏规则是( )
A.随机摸出一个球后放回,再随机摸出1个球
B.随机摸出一个球后不放回,再随机摸出1个球
C.随机摸出一个球后放回,再随机摸出3个球
D.随机摸出一个球后不放回,再随机摸出3个球
23.事件①:任意画一个多边形,其外角和为360°;事件②:经过一个有交通信号灯的十字路口,遇到红灯;则下列说法正确的是( )
A.事件①和②都是随机事件
B.事件①是随机事件,事件②是必然事件
C.事件①和②都是必然事件
D.事件①是必然事件,事件②是随机事件
24.暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加实践活动的概率为( )
A. B. C. D.
25.不透明的袋子中装有红、绿小球各一个,除颜色外两个小球无其他差别,从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,那么第一次摸到红球、第二次摸到绿球的概率是( )
A. B. C. D.
26.彩民李大叔购买1张彩票,中奖.这个事件是( )
A.必然事件 B.确定性事件 C.不可能事件 D.随机事件
27.一个袋子中装有4个相同的小球,它们分别标有号码1,2,3,4,摇匀后随机取出一球,记下号码后放回;再将小球摇匀,并从袋中随机取出一球,则第二次取出的球的号码不小于第一次取出的球的号码的概率为( )
A. B. C. D.
28.关于下列事件:(1)通常温度降到以下,纯净的水结冰;(2)随意翻到一本书的某页,页码是奇数;(3)明天太阳从东方升起;(4)购买1张彩票,中奖;描述正确的是( )
A.(1)(2)是随机事件,(3)(4)是必然事件
B.(1)(3)是随机事件,(2)(4)是必然事件
C.(1)(3)是必然事件,(2)(4)是随机事件
D.(1)(4)是必然事件,(2)(3)是随机事件
29.抛掷一枚质地均匀的硬币三次,恰有两次正面向上的概率是( )
A. B. C. D.
30.有两个事件,事件(1):购买1张福利彩票,中奖;事件(2):掷一枚六个面的点数分别为1,2,3,4,5,6的骰子,向上一面的点数不大于6.下列判断正确的是( )
A.(1)(2)都是随机事件 B.(1)(2)都是必然事件
C.(1)是必然事件,(2)是随机事件 D.(1)是随机事件,(2)是必然事件
31.童威把三张形状大小相同但画面不同的风景图片都按相同的方式剪成相同的三段,然后将三段上、三段中、三段下分别混合洗匀为“上、中、下”三堆图片,从这三堆图片中各随机抽取一张,则恰好能组成一张完整风景图片的概率是( )
A. B. C. D.
32.桌上倒扣着背面相同的5张扑克牌,其中3张黑桃、2张红桃.从中随机抽取一张,则( )
A.能够事先确定抽取的扑克牌的花色 B.抽到黑桃的可能性更大
C.抽到黑桃和抽到红桃的可能性一样大 D.抽到红桃的可能性更大
二、填空题
33.某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 50 100 200 500 1000
“射中9环以上”的次数 15 41 78 158 405 801
“射中9环以上”的频率
根据频率的稳定性,估计这名运动员射击一次“命中9环以上”的概率为 .
34.为了估计鱼塘中鱼的数量,养鱼者首先从鱼塘中打捞100条鱼,在每一条鱼身上做好记号后把这些鱼放归鱼塘,一段时间后再从鱼塘中打捞 50 条鱼.如果在这些鱼中有10条鱼是有记号的,那么估计鱼塘中鱼的条数为 .
35.三辆汽车经过丁字路口,可能向左转,也可能向右转,如果这两种可能性大小相同,那么这三辆汽车都朝一个方向转的概率是 .
36.某射击运动员在同一条件下的射击成绩记录如下:
射击次数 20 80 100 200 400 1000
“射中8环以上”的次数 18 68 82 168 327 823
“射中8环以上”的频率(结果保留两位小数) 0.90 0.85 0.82 0.84 0.82 0.82
根据频率的稳定性,估计这名运动员射击一次时“射中8环以上”的概率约是 .
37.某篮球运动员在罚球线上投篮的结果如下表所示:
投篮次数 50 100 150 200 250 300 500
投中次数m 28 60 78 104 123 152 251
投中频率 0.56 0.60 0.52 0.52 0.49 0.51 0.50
那么估计这名篮球运动员投篮一次投中的概率是 (结果精确到0.01).
38.某数学兴趣小组做“任意拋掷一枚图钉”的重复试验,多次试验后获得如下数据:
重复试验次数 10 50 100 500 1000
钉尖朝上次数 5 15 36 200 400
由此可以估计任意拋掷一次图钉,钉尖朝上的概率约为 .(结果精确到0.1)
39.小明在操场上做游戏,他在沙地上画了一个面积为的矩形,并在四个角画上面积不等的扇形,在不远处的固定位置向矩形内部投石子,记录如下(石子不会落在矩形外和各区域边缘):
投石子的总次数 50次 150次 300次 600次
石子落在空白区域内的次数 14次 85次 199次 400次
石子落在空白区域内的频率
依此估计空白部分的面积可能是 .
40.下图是由9个小正方形组成的图案,从图中随机取一点,这点在阴影部分的概率是 .
41.如图,矩形中,,E为的中点,连接.以E为圆心,长为半径画弧,分别与交于点F,G.向该矩形游戏板随机发射一枚飞针,则击中图中阴影部分区域的概率为 .
42.在一个不透明的口袋中有红色、黄色和绿色球共60个,它们除颜色外,其余完全相同,在不倒出球的情况下,发现摸到红球和绿球的频率分别稳定在和,由此推测口袋中黄球的个数是 个.
43.从,0,,,3.2这五个数中,随机抽取一个,则抽到无理数的概率是 .
44.甲、乙、丙三位同学把自己的数学课本故在一起,每人从中随机抽取一本(不放回),三位同学抽到的课本都是自己课本的概率是 .
45.如果所示的地板由15块方砖组成,每一块方砖除颜色外完全相同,小球自由滚动停在黑砖的概率为 .
46.如图,是由7个全等的正六边形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是 .
47.一只自由飞行的小鸟,如果随意落在如图所示的方格地面上(每个小方格形状完全相同),那么小鸟落在阴影方格地面上的概率是 .
48.某路口的人行造交通信号灯每分钟红灯亮秒,绿灯亮秒,黄灯亮5秒,当小明到达该路口时,遇到红灯的概率是 .
49.如图是可以自由转动的三个转盘,请根据下列情形回答问题(不考虑指针落在分界线上).
(1)转盘1被分成了2个扇形,圆心角为的扇形涂成红色,其余部分涂成白色,转动转盘1,当转盘1停止转动时,指针落在红色区域的概率是 .
(2)转盘2、转盘3都已被分成了3个相同的扇形,并且分别涂成红色、白色、黄色,同时转动转盘2和转盘3,当两个转盘停止转动时,则指针落在区域的颜色都是红色的概率为 .
50.把一枚均匀的硬币连续抛掷两次,两次正面朝上的概率是 .
51.如图,一块飞镖游戏板由大小相等的小正方形格子构成.向游戏板随机投掷一枚飞镖(每次飞镖均落在纸板上),击中阴影区域的概率是 .
52.如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为 .
53.如图,是一个圆盘及其内接正六边形,随机往圆盘内投飞镖,则飞镖落在正六边形内的概率是 .
三、解答题
54.第19届亚运会于2023年9月23日至10月8日在杭州成功举行,现有三张印有亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片,除正面图案不同外,其余均相同.
(1)从中随机抽取一张卡片,则抽出的卡片图案是“莲莲”的概率是________;
(2)从中随机抽取一张卡片,放回后再抽取一张,请用画树形图或列表法求抽出的两张卡片都是“莲莲”的概率.
55.某班数学兴趣小组进行如下活动:组长从一副扑克牌中选取六张分给两位同学,小明分到的三张扑克牌分别是方块,,;小亮分到的是方块,,.两人将分到的牌随机放在桌上(数字一面朝下),然后各自从对方的牌中抽一张进行比较,抽牌数字较大的人当“小老师”,给全班同学讲一个关于数学家的故事.
(1)若小亮从对方的扑克牌中抽一张,则抽到方块的概率是______;
(2)用列表法或画树状图法中的一种方法,求小明能当“小老师”的概率.
56.学校为增加节日气氛,在新年来临之际举行一次抽奖活动;如图是一个可以自由转动、质地均匀的转盘,每位学生都有一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品.下表是活动进行中的一组统计数据:
转动转盘的次数
落在“铅笔”的次数
落在“铅笔”的频率
(1)直接写出转动该转盘一次,获得铅笔的概率(结果保留小数点后两位),并直接写出饮料所在扇形的圆周角的度数(结果精确到);
(2)小明同学设计了一个摸球试验,在口袋中放一个白球和若干个红球,从中随机摸出一球,如果是白球,就获得饮料,如果是红球,就获得铅笔.并且这个试验中获得铅笔的概率跟学校抽奖活动的结果是一样的.
直接写出红球的个数;
直接写出两次摸球都获得饮料的概率.
57.一个不透明的袋子里有4个小球,小球上各标有一个数字,分别是1,2,4,7.这些小球除标有的数字不同外其他都相同.
(1)从这个袋子里随机摸出一个小球,摸出标有数字“2”的小球的概率是________;
(2)先从袋中随机摸出一个小球,记下小球上的数字后,放回、摇匀,再从袋子中随机摸出一个小球,记下小球上的数字,第一次记下的数放在十位,第二次记下的数放在个位组成两位数,请运用画树状图或列表的方法,求这个两位数是偶数的概率.
58.有5张看上去无差别的卡片,上面分别写着1,2,3,4,5.
(1)随机抽取1张卡片,则取出的卡片上数字为偶数的概率为______.
(2)若一次性抽取两张卡片,请用画树状图法或列表法求两张卡片上的数字和为奇数的概率.
59.A盒中有2个黄球、1个红球,B盒中有1个黄球、1个红球,这些球除颜色外无其他差别.
(1)若从A盒中随机取出1个球,则取出的球是红球的概率是______;
(2)若分别从每个盒中随机取出1个球,请用列表或画树状图的方法求取出的两个球中恰好是1个黄球、1个红球的概率.
60.在不透明的袋子里装有2个红球、1个蓝球(除颜色外其余都相同).
(1)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表的方法,求两次摸到一红一蓝的概率.
(2)若向袋中再放入若干个同样的蓝球,搅拌均匀后,使从袋中摸出一个蓝球的概率为,求后来放入袋中的蓝球个数.
61.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.
(1)随机摸出一个小球,直接写出小球标号是偶数的概率;
(2)随机一次摸出两个小球,用画树状图或列表的方法,求两个小球标号之和是偶数的概率;
(3)随机摸出一个小球然后放回,再随机摸出一个小球,直接写出两个小球标号之和是偶数的概率.
62.在一个不透明的纸盒里装有红、白、黄三种颜色的乒乓球4个(除颜色外完全相同),其中白球2个,红球、黄球各1个.
(1)从纸盒中随机摸出一个球,事件“摸到白球”的概率是______;
(2)若摸到红球得1分,摸到白球得2分,摸到黄球得3分.小明随机从纸盒中一次摸出两个球,请用画树状图法或列表法求小明至多得4分的概率.
63.一个不透明的布袋中装有1个红球,1个黑球和若干个白球,它们除颜色外其余都相同.从中任意摸出1个球,是白球的概率为.
(1)直接写出布袋中白球的个数;
(2)从布袋中先摸出一个球后放回,再摸出一个球,请用列表或画树状图法求两次摸到的球都是白球的概率.
64.党的十八大以来,某市以习近平新时代中国特色社会主义思想为指导,全面贯彻习主席关于扶贫开发的重要论述,在省委、省政府的坚强领导下,历经十年,全市减贫任务基本完成,脱贫攻坚取得阶段性成果,为了进一步巩固该成果,该市市委决定从甲、乙、丙、丁四名优秀共产党员中随机选取2名党员,到该市刚脱贫的某村庄蹲点指导工作,力争用五年的时间让该村村民走上致富之路.
(1)事件“甲、戊两名共产党员被选取到”是________事件;
(2)请用树状图或列表法求出恰好选取到甲和乙两名优秀共产党员的概率.
65.小明学习物理《电流和电路》后设计如图所示的一个电路图,其中、、分别表示三个可开闭的开关,“”表示小灯泡,“”表示电池.
(1)当开关闭合时,再随机闭合开关或其中一个,直接写出小灯泡发光的概率;
(2)当随机闭合开关、、中的两个,试用树状图或列表法求小灯泡发光的概率.
66.甲、乙两个不透明的盒子里分别装有3张卡片,其中甲盒里3张卡片分别标有数字1,2,3;乙盒里3张卡片分别标有数字4,5,6,这些卡片除数字外都相同,将卡片充分摇匀.
(1)从甲盒里随机抽取一张卡片,抽到的卡片上的数字为偶数的概率是______;
(2)从甲盒、乙盒里各随机抽取一张卡片,请用列表或画树状图的方法,求抽到的两张卡片上的数字之和能被3整除的概率.
67.从甲、乙、丙、丁4名学生中选2名学生参加一次乒乓球单打比赛,求下列事件发生的概率.
(1)甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是 ;
(2)任意选取2名学生参加比赛,求一定有乙的概率.(用树状图或列表的方法求解).
68.一只不透明袋中装有1个白球和若干个红球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从袋中摸出1个球,记下颜色后放回、揽匀,不断重复这个过程,获得数据如下:
摸球的次数 200 300 400 1000 1600 2000
摸到白球的频数 72 93 130 334 532 667
摸到白球的频率 0.03600 0.03100 0.03250 0.03340 0.03325 0.03335
(1)该小组发现,摸到白球的频率在一个常数附近摆动,这个常数是______(精确到0.001),由此估出红球有______个;
(2)现从该袋中随机摸出一个球,不放回,再摸出一个球,请用画树状图或列表法求恰好摸到1个白球和1个红球的概率.
69.箱子里有3个红球和2个黄球,从箱子中一次拿出两个球出来.
(1)请你用列表或画树形图的方法,求一次拿出的两个球正好是一红一黄的概率;
(2)直接写出两个球都是红球的概率.
70.在5张相同的小纸条上,分别写有语句:①函数表达式为;②函数表达式为;③函数的图像关于原点对称;④函数的图像关于轴对称;⑤函数值随自变量增大而增大.将这5张小纸条做成5支签,①、②放在不透明的盒子中搅匀,③、④、⑤放在不透明的盒子中搅匀.
(1)从盒子中任意抽出1支签,抽到①的概率是______;
(2)先从盒子中任意抽出1支签,再从盒子中任意抽出1支签.求抽到的2张小纸条上的语句对函数的描述相符合的概率.
71.经过某十字路口的汽车可能直行也可能左转或者右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率.
(1)两辆车向左转,一辆向右转;
(2)至少有两辆车向右转.
72.一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.甲从口袋中随机摸取一个小球,记下标号m,然后放回,再由乙从口袋中随机摸取一个小球,记下标号n,组成一个数对(m,n).
(1)用列表法或画树状图法,写出(m,n)所有可能出现的结果;
(2)甲、乙两人玩游戏,规则如下:按上述要求,两人各摸取一个小球,小球上标号之和为奇数则甲赢,小球上标号之和为偶数则乙赢.你认为这个游戏规则公平吗?请说明理由.
73.不透明的袋子中装有红色小球1个、绿色小球2个,除颜色外无其它差别.
(1)从袋中随机摸出一个小球,直接写出摸到红球的概率;
(2)随机摸出一个小球,记下颜色,放回并摇匀,再随机摸出一个,求两次都摸到绿球的概率.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A A B B C B B B C
题号 11 12 13 14 15 16 17 18 19 20
答案 C A A D A A A B B D
题号 21 22 23 24 25 26 27 28 29 30
答案 C A D B A D D C C D
题号 31 32
答案 B B
1.B
【分析】本题考查了必然事件.熟记事件分类及相应概念是解决问题的关键.
根据必然事件的定义进行判断作答即可.
【详解】解:由题意知,从袋子中随机摸出3个球,
至少有1个是白球为随机事件,故A不符合要求;
至少有1个是红球为必然事件,故B符合要求;
至少有2个是红球为随机事件,故C不符合要求;
至少有2个是白球为随机事件,故D不符合要求;
故选:B.
2.A
【分析】本题考查事件的分类,根据一定条件下,可能发生,可能不发生的事件为随机事件,进行判断即可.
【详解】解:“翻开人教版《数学》九年级下册课本恰好翻到第56页”这个事件是随机事件;
故选A.
3.A
【分析】本题考查了必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
【详解】解:事件(1)是随机事件;事件(2)是随机事件;
故选A.
4.B
【分析】画出树状图,求得所有等可能的结果数,再得到只有一辆汽车向左转的结果数,然后利用概率公式求解即可;
【详解】解:根据题意,画出树状图,如图,
由图知,一共有27种等可能的结果,其中只有一辆汽车向左转的结果有12种,
∴只有一辆汽车向左转的概率为.
故选:B.
5.B
【分析】本题考查了随机事件,通过概率说明可能性大小,理解随机事件,掌握概率计算公式是解题的关键.
【详解】解:A.从中随机抽取1个球,抽到红球的概率为,抽到蓝球的概率为,结论正确,不符合题意;
B.从中随机抽取1个球,抽到红球的概率为,抽到蓝球的概率为,结论错误,符合题意;
C.因为只有个红球,所以从中随机抽取6个球,至少有个是蓝色的,结论正确,不符合题意;
D.从中随机抽取5个球,可能都是红色的,结论正确,不符合题意;
故选:B.
6.C
【分析】本题主要考查了用树状图求等可能事件的概率,方法是用树状图或列表法列举出所有可能出现的结果总数,找出符合条件的结果数,用分数表示即可,注意每种情况发生的可能性相等.先利用画树状图,得出所有可能出现的结果总数,从中找到符合条件的结果数,然后求出概率即可.
【详解】解:根据题意,画出树状图,如图,
由图知,一共有27种等可能的结果,其中至少有两辆车直行的结果有7种,
∴至少有两辆车直行的概率为.
故选:C.
7.B
【分析】此题考查了事件的分类,事件分为随机事件和确定事件,确定事件包含必然事件和不可能事件,据此进行判断即可.
【详解】解:“经过有交通信号灯的路口,遇到黄灯”这个事件是随机事件,
故选:B
8.B
【分析】本题主要考查了事件的分类,解题的关键是理解题意,弄清成语的含义.根据事件的分类进行解答即可.
【详解】解:A.旭日东升是必然事件,故A不符合题意;
B.心想事成是随机事件,故B符合题意;
C.水中捞月是不可能事件,故C不符合题意;
D.只手遮天是不可能事件,故D不符合题意.
故选:B.
9.B
【分析】本题考查了列表法与树状图法:利用列表法或树状图法展示所有可能的结果求出,再从中选出符合事件A或的结果数目,然后根据概率公式计算事件A或事件的概率.
先画树状图得出所有等可能结果数,从中找到“关联数”的结果数,再根据概率公式求解即可.
【详解】解:画树状图,
由图可知,所有可能组成的数有123、132、213、231、312、321,共有6种,其中恰好是“关联数”的有123、321,共 2种,
所以恰好是“关联数”的概率为,
故选:B.
10.C
【分析】本题主要考查随机事件的概念,它与必然事件,不可能事件相对.
解题的关键是熟练掌握各个概念“随机事件是可能发生也可能不发生的事件;必然事件就是一定发生的事件;不可能事件就是一定不发生的事件”;据此解答即可.
【详解】解:A,B,D都是不可能事件.
所以是随机事件的是守株待兔.
故选:C.
11.C
【分析】
画出树状图,再根据概率公式计算即可得;
本题主要考查画树状图或列表法求概率,得到所求的情况数是解决本题的关键.
【详解】画树状图如下:
由树状图可知共有8种等可能结果,其中恰有两次正面向上的有3种,
所以恰有两次正面向上的概率为,
故选:C.
12.A
【分析】根据随机事件的定义即可得出答案.
【详解】解:∵通常温度降到0℃以下,纯净的水会结冰,
∴这个事件是必然事件.
故选:A.
【点睛】本题考查的是必然事件,不可能事件,随机事件的概念.必然事件指在一定条件下, 一定发生的事件,不可能事件是指在一定条件下, 一定不发生的事件,不确定事件即随机事件是指在一定条件 下,可能发生也可能不发生的事件.
13.A
【分析】分别求出每个选项中的概率,和由频率统计图估计出的概率作比较即可得出答案
【详解】解:、选项中取到红球的概率是,、选项中出现点的概率是,、选项中出现正面的概率是,、选项中能被整除的概率即为偶数的概率为,
由图知,随着试验次数的增加,频率逐渐稳定在附近,所以符合条件的只有.
故选:.
【点睛】本题考查了频率估计概率,利用概率公式求概率,正确求出每项概率和由频率估计出的概率作比较是解答本题的关键.
14.D
【分析】根据题意列出表格,得出所有等可能的情况数,找出随机取出一把钥匙开任意一把锁,一次打开锁的情况数,即可求出所求的概率.
【详解】解:列表得:
锁1 锁2
钥匙1 (锁1,钥匙1) (锁2,钥匙1)
钥匙2 (锁1,钥匙2) (锁2,钥匙2)
钥匙3 (锁1,钥匙3) (锁2,钥匙3)
由表可知,所有等可能的情况有6种,其中随机取出一把钥匙开任意一把锁,一次打开锁的2种,
则P(一次打开锁).
故选D.
【点睛】本题考查列表法与树状图法求概率,掌握概率等于所求情况数与总情况数之比是解题的关键.
15.A
【分析】根据频数和频率的关系进行判断即可
【详解】A. 如果继续对这批羽毛球进行质量检验,优等品的频率将在0.94附近摆动,故此选项正确;
B. 从这批羽毛球中任意抽取一只,不一定是优等品,故此选项错误;
C. 从这批羽毛球中任意抽取50只,优等品有不一定为47只,故此选项错误;
D. 从这批羽毛球中任意抽取1100只,优等品的频率不一定在0.940~0.941的范围内,故此选项错误.
故选:A.
【点睛】本题主要考查利用频率估计概率的知识,熟练掌握利用频率估计概率的知识是解题的关键.
16.A
【分析】依据“随机事件:在一定条件下有可能发生也有可能不发生的事件”、“必然事件:在一定条件下一定会发生的事件”、“不可能事件:在一定条件下一定不会发生的事件”进行判断即可、“确定性事件:包括必然事件和不可能事件”进行判断即可.
【详解】解:“守株待兔”是随机事件,
故选:A.
【点睛】本题考查了随机事件、必然事件、不可能事件;熟记相关概念是解题的关键.
17.A
【分析】画树状图得出所有等可能的结果数,再从中找到符合条件的结果数,然后再用概率公式求解即可.
【详解】解:树状图如图所示,
一共有12种等可能性,其中王明选中的卡片中有偶数的可能性有10种可能性,
故王明选中的卡片中有偶数的概率为:,
故选:A.
【点睛】本题主要考查的是用列表法或树状图法求概率,列表法可以重复不遗漏的列出所有可能的结果,适合于两步完成的事件,树状图法适合两步或两步以上完成的事件,用到的知识点为:概率等于所求情况数与总情况数之比.
18.B
【分析】根据题意列出树状图求出各种颜色求得概率,逐个判断即可得到答案;
【详解】解:由题意可得,
摸出红球的概率为,摸出黄球的概率为:,摸出黑球的概率为:,
故选B;
【点睛】本题考查概率定义及树状图法求概率,解题的关键是正确理解概率的定义.
19.B
【分析】依据题意先用画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率.
【详解】解:由题意,画树状图得∶
∴一共有12种情况,第一节上数学课,第四节上语文课只有1种情况,
∴第一节上数学课,第四节上语文课的概率为 .
故选B.
【点睛】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏地列出所有可能的结果,适合于两步完成的事件.用到的知识点为∶概率=所求情况数与总情况数之比.
20.D
【分析】根据白球两个,摸出三个球必然有一个黑球.
【详解】解:A袋子中装有4个黑球和2个白球,摸出的三个球中可能为两个白球一个黑球,所以A不是必然事件;
B.C.袋子中有4个黑球,有可能摸到的全部是黑球,B、C有可能不发生,所以B、C不是必然事件;
D.白球只有两个,如果摸到三个球不可能都是白梂,因此至少有一个是黑球,D正确.
故选D.
【点睛】本题考查随机事件,解题关键在于根据题意对选项进行判断即可.
21.C
【分析】本题主要考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件;不可能事件是指在一定条件下,一定不发生的事件;不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.熟知这三类事件的区别是解题的关键.
根据这三类事件的定义,逐项判断即可求解.
【详解】解:A.打开电视机,正在直播足球比赛是随机事件,故本选项不符合题意;
B.在只装有2个玻球的袋中摸出一个球是黑球是随机事件,故本选项不符合题意;
C.掷一次骰子,向上的一面出现的点数大于7是不可能事件,故本选项符合题意;
D.当室外温度低于时,一碗清水在室外会结冰是必然事件,故本选项不符合题意;
故选:C.
22.A
【分析】根据树形图,可得此次摸球的游戏规则是:随机摸出一个球后放回,再随机摸出1个球
【详解】解:观察树状图可得:袋子中共有红、黄、蓝三个小球,此次摸球的游戏规则是随机摸出一个球后放回,再随机摸出1个球,
故选:A.
【点睛】此题考查列表法与树状图法求概率,解题关键在于利用树状图进行解答.
23.D
【分析】根据随机事件和必然事件的概念判断可得.
【详解】解:事件①:任意画一个多边形,其外角和为360°,这是必然事件;
事件②:经过一个有交通信号灯的十字路口,遇到红灯,这是随机事件;
故选:D.
【点睛】本题考查的是理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
24.B
【详解】解:画树状图得:
∵共有9种等可能的结果,小明和小亮选到同一社区参加实践活动的有3种情况,
∴小明和小亮选到同一社区参加实践活动的概率为:
故选B
25.A
【分析】首先根据题意画出树状图,由树状图求得所有等可能的结果与第一次摸到红球,第二次摸到绿球的情况,然后利用概率公式求解即可求得答案.
【详解】解:画树状图得:
∵共有4种等可能的结果,第一次摸到红球,第二次摸到绿球有1种情况,
∴第一次摸到红球,第二次摸到绿球的概率为,
故选:A.
【点睛】本题考查了画树状法或列表法求概率,列出所有等可能的结果是解决本题的关键.
26.D
【分析】直接根据随机事件的概念即可得出结论.
【详解】购买一张彩票,结果可能为中奖,也可能为不中奖,中奖与否是随机的,即这个事件为随机事件.
故选:D.
【点睛】本题考查了随机事件的概念,解题的关键是熟练掌握随机事件发生的条件,能够灵活作出判断.
27.D
【分析】列树状图或画表格得到所有可能情况,然后找出第二次取出的球的号码不小于第一次取出的球的号码的情况,计算概率即可.
【详解】解:列树状图为:
由上图可知共16种等可能情况,符合要求的共有10种结果,
故第二次取出的球的号码不小于第一次取出的球的号码的概率为.
故选D.
【点睛】本题考查概率公式,解题的关键是能用树状图或列表法表示所有等可能情况.
28.C
【分析】必然事件: 在一定条件下,一定会发生的事件,叫做必然事件,随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件;根据概念判断即可.
【详解】(1)通常温度降到以下,纯净的水结冰,是必然事件;
(2)随意翻到一本书的某页,页码是奇数,是随机事件;
(3)明天太阳从东方升起,是必然事件;
(4)购买1张彩票,中奖,是随机事件;
故选:C.
【点睛】本题考查的是随机事件与必然事件的含义,掌握“利用概念判断随机事件与必然事件”是解本题的关键.
29.C
【分析】根据随机掷一枚质地均匀的硬币三次,可以分别假设出三次情况,画出树状图即可.
【详解】解:列树状图如下所示:
根据树状图可知一共有8种等可能性的结果数,恰好有两次正面朝上的事件次数为:3,
∴恰好有两次正面朝上的事件概率是:.
故选C.
【点睛】本题主要考查了树状图法求概率,解题的关键是根据题意画出树状图.
30.D
【分析】必然事件: 在一定条件下,一定会发生的事件,叫做必然事件,随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫做随机事件;根据概念判断即可.
【详解】解:事件(1):购买1张福利彩票,中奖,是随机事件,
事件(2):掷一枚六个面的点数分别为1,2,3,4,5,6的骰子,向上一面的点数不大于6,是必然事件,
故选D
【点睛】本题考查的是随机事件与必然事件的含义,掌握“利用概念判断随机事件与必然事件”是解本题的关键.
31.B
【分析】把三张风景图片用甲、乙、丙来表示,根据题意,画出树状图,得出可能出现的结果及满足条件的结果,利用概率公式求解即可得.
【详解】解:把三张风景图片用甲、乙、丙来表示,根据题意,画出如下树状图:
从树状图可得:所有可能出现的结果共有27种,这些结果出现的可能性相同,其中恰好组成一张完整风景图片的可能有3种,
∴三张图片恰好组成一张完整风景图片的概率为:,
故选:B.
【点睛】题目主要考查列表法或树状图法求概率,理解题意,熟练掌握运用列表法或树状图法是解题关键.
32.B
【分析】要求可能性的大小,只需求出各自所占的比例大小即可.求比例时,应注意记清各自的数目.
【详解】解:A、因为袋中扑克牌的花色不同,所以无法确定抽取的扑克牌的花色,故本选项错误;
B、因为黑桃的数量最多,所以抽到黑桃的可能性更大,故本选项正确;
C、因为黑桃和红桃的数量不同,所以抽到黑桃和抽到红桃的可能性不一样大,故本选项错误;
D、因为红桃的数量小于黑桃,所以抽到红桃的可能性小,故本选项错误.
故选B.
33./
【分析】本题考查了利用频率估计概率,解决本题的关键是理解当试验的所有可能结果不是有限个或结果个数很多,或各种可能结果发生的可能性不相等时,一般通过统计频率来估计概率.大量重复试验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
【详解】解:根据表格数据可知:
根据频率稳定在,估计这名运动员射击一次时“射中9环以上”的概率是.
故答案为:.
34.500条
【分析】本题考查了用样本估计总体;设鱼塘中鱼的条数为x条,根据题意得,求解即可.
【详解】解:设鱼塘中鱼的条数为x条,
根据题意得:,
解得:.
故答案为:500条.
35.
【分析】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果,再从中选出符合事件或的结果数目,然后利用概率公式计算事件或事件的概率.
画树状图展示所有种等可能的结果数,再找出三辆汽车都朝一个方向转的结果数,然后根据概率公式求解即可.
【详解】画树状图为:
共有种等可能的结果数,其中三辆汽车都朝一个方向转的结果数为,
所以至少有两辆车向右转的概率为,
故答案为:.
36.
【分析】本题考查用频率估计概率,根据大量的实验结果稳定在,即可得出结论.
【详解】解:由题知,射击次数越多,“射中8环以上”的频率越接近,
所以这名运动员射击一次时“射中8环以上”的概率约是.
故答案为:.
37.0.50
【分析】根据频率估计概率的方法,结合表格数据即可得出答案.
【详解】解:由频率分布表可知,随着投篮次数越来越大,频率逐渐稳定到常数附近,
则估计这名球员在罚球线上投篮一次投中的概率为,
故答案为:.
【点睛】本题考查了利用频率估计概率,解题的关键是理解这种概率的得出是在大量实验的基础上得出的,不能单纯的依靠几次决定.
38.0.4
【分析】此题主要考查了利用频率估计概率,首先通过实验得到事件的频率,然后用频率估计概率即可解决问题.观察表格的数据求出每次试验得到的频率可以得到图钉钉尖朝上的频率,然后用频率估计概率即可求解.
【详解】解:表中图钉钉尖朝上的频率分别为,,,,
图钉钉尖朝上频率逐渐稳定在0.40左右,
估计任意抛掷一枚图钉,图钉钉尖朝上的概率约为0.4.
故答案为:0.4
39.4
【分析】本题主要是利用频率估计概率、概率的应用等知识点,掌握当实验次数越多时,某事件的频率越接近于该事件的概率是解题的关键.
根据投在空白区域内的频率得到概率的大小,由此计算空白区域的面积即可.
【详解】解:由表格可知:
当投石子的次数越来越多时,石子落在空白区域的频率越接近,即空白区域的面积占总面积的,
∴空白部分的面积=.
故选答案为4.
40.
【分析】直接根据几何概率求解即可.
【详解】解:图中共有9个小正方形,其中阴影部分共有5个小正方形,
∴从图中随机取一点,这点在阴影部分的概率是,
故答案为:.
【点睛】本题考查几何概率求解,理解并掌握几何概率是解题关键.
41.
【分析】本题考查了矩形的性质和不规则面积的计算,利用矩形的性质求得,进而可得,然后根据解答即可.熟练掌握矩形的性质、明确阴影面积为两个全等的等腰直角三角形的面积减去两个圆心角为的扇形面积是解题关键.
【详解】解:∵四边形是矩形,,,E为的中点,
,,
,
,
∴击中图中阴影部分区域的概率为;
故答案为:.
42.24
【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,用频率估计概率可知黄色球的数量为总数乘以其所占百分比.
【详解】解:根据题意得:
(个),
答:此推测口袋中黄球的个数是24个.
故答案为:24.
【点睛】本题主要考查频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.
43.
【分析】利用简单的概率公式计算即可.
【详解】∵一共有5种等可能性,无理数有,共2种等可能性,
∴抽到无理数的概率是.
故答案为:.
【点睛】本题考查了简单的概率公式求概率,熟练掌握公式是解题的关键.
44.
【分析】画出树状图,根据树状图即可得出答案.
【详解】设甲的数学课本用表示,乙的数学课本用表示,丙的数学课本用表示,画树状图如下:
由树状图可知,共有六种等可能的结果数,其中三位同学抽到的课本都是自己的课本有一种结果,所以三位同学抽到的课本是自己课本的概率是.
【点睛】本题主要考查概率的计算,熟练掌握概率的计算方法是解决本题的关键.
45.
【分析】本题考查了几何概率,把黑色方砖的面积除以总面积,即可作答.
【详解】解:∵总面积为15块方砖的面积,且每个其中方砖的面积是相等的,黑色方砖有5块,
∴小球停在黑色方砖的概率为,
故答案为:
46.
【分析】根据阴影部分的面积所占比例得出概率即可.
【详解】解:由图知,阴影部分的面积占图案面积的,即这个点取在阴影部分的概率是,
故答案为:.
【点睛】本题考查几何概率.熟练掌握几何概率的计算方法,是解题的关键.
47.
【详解】∵由题意和图可知,阴影部分的面积占整个方格地面的比值为:,
∴小鸟落在阴影方格地面上的概率为:.
48.
【分析】本题考查了概率,根据题意和概率公式即可得,掌握概率公式是解题的关键.
【详解】解:∵每分钟红灯亮秒,绿灯亮秒,黄灯亮5秒,
∴当小明到达该路口时,遇到红灯的概率:,
故答案为:.
49.
【分析】本题考查几何概率、用列表法或树状图法求概率,熟知求几何概率可利用长度比、面积比、体积比等.
(1)用红色区域的面积除以圆面积可求解;
(2)用列表法得到所有的等可能的结果,进而得到符合条件的结果数,利用求概率公式即可.
【详解】解:(1)根据题意,当转盘1停止转动时,指针落在红色区域的概率是,
故答案为:;
(2)列表为
红 白 黄
红 红红 白红 黄红
白 红白 白白 黄白
黄 红黄 白黄 黄黄
由表知,共有9种等可能的结果,其中指针落在区域的颜色都是红色的有1种,
∴指针落在区域的颜色都是红色的概率为,
故答案为:.
50.
【分析】举出所有情况,看正面都朝上的情况数占总情况数的多少即可.
【详解】解:共4种情况,正面都朝上的情况数有1种,所以概率是.
故答案为:.
考点:列表法与树状图法.
51.
【分析】根据几何概率的求解公式即可求解.
【详解】解:设图中每个小正方形的面积为1,则大正方形的面积为9,
根据题意图中阴影部分的面积为3,
则P(击中阴影区域).
故答案为:.
【点睛】此题主要考查概率的求解,解题的关键是熟知几何概率的公式.
52.
【分析】用正方形的内切圆的面积的一半除以正方形的面积得到针尖落在黑色区域内的概率.
【详解】解:设正方形的边长为,
∵黑色区域面积为正方形的内切圆的面积的一半,
∴针尖落在黑色区域内的概率.
故答案为:.
【点睛】本题考查了几何概率:某事件的概率某事件所占有的面积与总面积之比.
53.
【分析】设圆的半径为,先分别求出圆的面积和正六边形的面积,再利用概率公式即可得.
【详解】解:如图,设圆的圆心为点,半径为,过点作于点,连接,
则圆的面积为,,
图中的六边形是正六边形,
,
是等边三角形,
,
正六边形的面积为,
则飞镖落在正六边形内的概率是,
故答案为:.
【点睛】本题考查了求概率、圆与正六边形等知识点,熟练掌握概率的求法是解题关键.
54.(1)
(2)
【分析】
本题考查列表法与树状图法、概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
(1)直接利用概率公式可得答案.
(2)画树状图得出所有等可能的结果数以及两次抽到的卡片都是“莲莲”的结果数,再利用概率公式可得出答案.
【详解】(1)解:由题意得,从这三张卡片中随机抽取一张,图案恰好是“莲莲”的概率为.
故答案为:;
(2)解:将琮琮、宸宸和莲莲的不透明卡片分别记为A,B,C,
画树状图如下:
共有9种等可能的结果,其中两次抽到图案都是“莲莲”的结果有1种,
∴两次抽到图案都是“莲莲”的概率为.
55.(1)
(2)
【分析】(1)共三张,每一张被抽到的概率都是相等的;
(2)列出表格,根据要求计算相应结果数量与总数量的比值即可.
【详解】(1)解:抽到方块的概率是,
故答案为:;
(2)解; 根据题意列表如下:
小明 小亮
由表可以看出,所有可能出现的结果共有种,这些结果出现的可能性相等.
其中小明取出的牌比小亮大的结果有,,共种.
(小明能当小老师).
【点睛】本题考查了简单的概率计算,掌握列表法或画树状图法是解题关键.
56.(1),;
(2) 个; .
【分析】()根据图表中的频率去估计概率及用即可;
()利用概率公式,摸到白球的概率为,摸到红球的概率为即可求解;
画树状图,然后利用概率公式求解;
本题考查了利用频率估计概率和列表法与树状图法求概率,解题的关键是灵活运用知识点的应用.
【详解】(1)根据表格可知:转动该转盘一次,获得铅笔的概率为,
饮料所在扇形的圆周角的度数;
(2)设红球的个数有个,
由()得,铅笔的概率为,
,解得:,
经检验:是分式方程的解,
∴红球的个数有个;
列表如下:
白 红 红 红
白 白、白 红、白 红、白 红、白
红 白、红 红、红 红、红 红、红
红 白、红 红、红 红、红 红、红
红 白、红 红、红 红、红 红、红
共有种等可能的结果数,其中两人都获得“饮料”的结果数为,
∴两人都获得“饮料”的概率为.
57.(1)
(2)
【分析】本题考查列表法与树状图法、概率公式,解答本题的关键是明确题意,画出相应的树状图,求出相应的概率.
(1)直接运用概率公式计算即可;
(2)根据题意可以画出相应的树状图,然后即可求出这个两位数是偶数的概率.
【详解】(1)解:由题意可得,
从袋中机摸出一个小球,则摸出标有数字“2”的小球的概率是.
(2)解:画树状图如下
由树状图可知一共有16种可能,且每种结果出现的可能性相同,其中这个两位数是偶数的结果数有8种,
这个两位数是偶数的概率为.
58.(1)
(2)
【分析】本题考查简单概率计算,利用列表法和树状图法计算概率.
(1)根据题意列式计算即可;
(2)根据题意列表列出等可能性即可得到本题答案.
【详解】(1)解:∵有5张看上去无差别的卡片,上面分别写着1,2,3,4,5,
∴偶数卡片为,
∴设取出的卡片上数字为偶数的结果为事件A.
∴;
(2)解:根据题意列表如下:
,
由上表可知,一次性抽取两张卡片,有20种等可能的结果,其中“两张卡片上数字和为奇数”的结果有12种.
∴P(两张卡片上数字和为奇数).
59.(1)
(2)树状图见解析,概率是
【分析】本题考查了概率的应用,掌握概率的计算公式以及树状图或列表法是解题关键.
(1)根据题意即可求解;
(2)画出树状图,确定可能出现的所有结果以及满足条件的结果数,即可求解.
【详解】(1)解:若从A盒中随机取出1个球,则取出的球是红球的概率是:;
故答案为:
(2)解:画树状图:
由树状图得共有6种等可能结果,其中取出的两个球中恰好1个黄球、1个红球的有3种结果,
(1黄1红).
60.(1) ;(2)9个
【分析】(1)根据题意画出树状图后,数出可能的结果总数及两次摸到不同颜色球的结果数,再根据概率的意义可得解;
(2)设放入x个蓝球,再根据概率的意义得到方程,解方程后可以得解.
【详解】解:(1)如图所示,
共有6种可能结果,每种结果发生的可能性相等;
其中两次摸到不同颜色球包含其中4种结果,
所以两次摸到不同颜色球的概率为;
(2)设放入x个蓝球,
由题意,得: ,
解得: x=9,
经检验, x=9 是原方程的解,
所以,放入袋中的蓝球为9个.
【点睛】本题考查概率的应用,熟练掌握概率的意义、树状图求概率的方法及方程思想方法的应用是解题关键.
61.(1)
(2)
(3)
【分析】本题考查列表法与树状图法、概率公式.
(1)直接利用概率公式可得答案.
(2)列表可得出所有等可能的结果数以及两个小球标号之和是偶数的结果数,再利用概率公式可得出答案.
(2)列表可得出所有等可能的结果数以及两个小球标号之和是偶数的结果数,再利用概率公式可得出答案.
【详解】(1)解:1,2,3,4中为偶数的是2和4,
∴随机摸出一个小球,标号是偶数的概率为.
(2)解:列表如下:
1 2 3 4
1
2
3
4
由表格可知,共有12种等可能的结果,其中两个小球标号之和是偶数的结果有:,,共4种,
∴两个小球标号之和是偶数的概率为.
(3)解:列表如下:
1 2 3 4
1
2
3
4
由表格可知,共有16种等可能的结果,其中两个小球标号之和是偶数的结果有:,,共8种,
∴两个小球标号之和是偶数的概率为.
62.(1)
(2)
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有12种等可能的结果,其中小明至多得4分的结果有8种,再由概率公式求解即可.
【详解】(1)解:由题意,共4种等可能结果,其中符合题意的结果有2种,
∴事件“摸到白球”的概率是,
故答案为:;
(2)画树状图如下:
共有12种等可能的结果,其中小明至多得4分的结果有8种,
∴小明至多得4分的概率为.
【点睛】本题考查的是树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
63.(1)2个
(2)
【分析】(1)设布袋中白球的个数为x个,根据概率公式列出方程,即可求解;
(2)根据题意,画出树状图,可得一共有16种等可能情况,其中两次都摸到白球的有4次,再根据概率公式计算,即可求解.
【详解】(1)解:设布袋中白球的个数为x个,根据题意得:
,
解得:.
经检验:是原方程的解,且符合题意,
即布袋中白球的个数为2个;
(2)解:根据题意,画出树状图,如下:
一共有16种等可能情况,其中两次都摸到白球的有4次,
∴ 两次摸到的球都是白球的概率为.
【点睛】本题考查列表法或树状图法求概率,熟练掌握概率公式是解题关键.
64.(1)随机
(2)
【分析】(1)甲、戊两名共产党员可能被选取到,也可能不被选取到,因此事件“甲、戊两名共产党员被选取到”是随机事件.
(2)先列表格或画树状图求出恰好选取到甲和乙两名优秀共产党员的所有可能结果,再代入概率的计算公式计算即可.
【详解】(1)事件“甲、戊两名共产党员被选取到”是随机事件,
故答案为:随机
(2)列表格如下
甲 乙 丙 丁
甲 甲乙 甲丙 甲丁
乙 乙甲 乙丙 乙丁
丙 丙甲 丙乙 丙丁
丁 丁甲 丁乙 丁丙
一共有12中结果,其中恰好选取到甲和乙的有两种结果,
∴恰好选取到甲和乙的概率=.
【点睛】本题主要考查了事件的分类及概率的计算,熟练掌握表格法和树状图法求事件发生的概率是解题的关键.
65.(1)
(2)
【分析】(1)根据电路图可知,当开关闭合时,想要小灯泡发光,只有闭合,从而可得出随机闭合开关或其中一个,小灯泡发光的概率;
(2)用树状图或列表法列出所有的情况,再找出能让小灯泡发光的情况,利用概率公式求解即可.
【详解】(1)解:当开关闭合时,想要小灯泡发光,只有闭合,
随机闭合开关或其中一个,小灯泡发光的概率为;
(2)法一:画出树状图如下:
共有6种等可能结果,其中能使小灯泡发光的组合共有4种,故(小灯泡发光).
法二:
列表如下:
(,) (,)
(,) (,)
(,) (,)
共有6种等可能结果,其中能使小灯泡发光的组合共有4种,故P(小灯泡发光).
【点睛】本题考查了用树状图或列表法求概率,解题的关键是结合物理知识,知道必须闭合,且闭合或中一个,小灯泡才会发光.
66.(1)
(2)
【分析】(1)由概率公式即可得出结果;
(2)画出树状图,由树状图求得所有等可能的结果与抽到的两张卡片上标有的数字之和能被3整除的结果,再由概率公式即可求得答案.
本题考查了树状图法求概率.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
【详解】(1)解:从甲盒里随机抽取一张卡片,抽到的卡片上标有数字为偶数的概率是,
故答案为:;
(2)解:画树状图如下:
共有9种等可能的结果,其中两张卡片的数字之和能被3整除的结果有3种,
抽到的两张卡片上标有数字之和能被3整除的概率为.
67.(1)
(2)
【分析】(1)利用例举法例举所有的等可能的情况数,再利用概率公式进行计算即可;
(2)先列表得到所有的等可能的情况数以及符合条件的情况数,再利用概率公式进行计算即可.
【详解】(1)解:由甲一定参加比赛,再从其余3名学生中任意选取1名,共有甲、乙,甲、丙,甲、丁三种等可能,符合条件的情况数有1种,
∴甲一定参加比赛,再从其余3名学生中任意选取1名,恰好选中丙的概率是
(2)列表如下:
甲 乙 丙 丁
甲 甲、乙 甲、丙 甲、丁
乙 乙、甲 乙、丙 乙、丁
丙 丙、甲 丙、乙 丙、丁
丁 丁、甲 丁、乙 丁、丙
所有所有的等可能的情况数有12种,符合条件的情况数有6种,
所以一定有乙的概率为:
【点睛】本题考查的是利用例举法,列表的方法求解简单随机事件的概率,概率公式的应用,掌握“例举法与列表法求解概率”是解本题的关键.
68.(1)0.033,2
(2)
【分析】本题考查用频率估计概率、列表法或树状图法求概率,正确得到所有的等可能的结果是解答的关键.
(1)通过大量的实验,摸到白球的频率在一个常数附近摆动,这个常数可作为摸到白球的概率,进而可求解;
(2)利用列表法得到所有的等可能结果,再找出符合条件的结果数,然后利用求概率公式求解即可.
【详解】(1)解:由表可知,摸到白球的频率在一个常数附近摆动,这个常数为0.033,由此估出红球有
个,
故答案为:0.033,2;
(2)解:列表为:
白 红 红
白 红白 红白
红 白红 红红
红 白红 红红
由表知,共有6种等可能的结果,其中恰好摸到1个白球和1个红球的有4种,故恰好摸到1个白球和1个红球的概率为.
69.(1);
(2).
【分析】(1)根据题意画出树状图,求出所有可能数和符合条件数,运功概率公式求解即可;
(2)结合树状图,求出所有可能数和符合条件数,运功概率公式求解即可.
【详解】(1)解:画树状图:
由树状图可知,从箱子中一次拿出两个球共有种可能,
两个球正好是一红一黄的可能有种,
所以一次拿出的两个球正好是一红一黄的概率为:
答:一次拿出的两个球正好是一红一黄的概率为.
(2)由树状图可知,从箱子中一次拿出两个球共有种可能,
两个球都是红球的可能有6种,
所以两个球都是红球的概率为:
故答案为:.
【点睛】本题考查了无放回的随机抽样的概率求解;正确画出树状图、结合题意分析出符合条件的可能数是解题的关键.
70.(1)
(2)
【分析】(1)直接由概率公式求解即可;
(2)画出树状图,再由概率计算公式求解即可.
【详解】(1)解:从盒子中任意抽出1支签,抽到①的概率是;
故答案为:;
(2)解:画出树状图:
共有6种结果,抽到的2张小纸条上的语句对函数的描述相符合的有①、③和①、⑤和②、④共3种,
抽到的2张小纸条上的语句对函数的描述相符合的概率为.
【点睛】本题主要考查了列表法或树状图求概率,一次函数与二次函数的性质,解题的关键是会列出表或树状图以及一次函数与二次函数的性质.
71.(1)
(2)
【分析】(1)画出树状图,求得所有等可能的结果数,再得到两辆车向左转,一辆向右转的结果数,然后利用概率公式求解即可;
(2)根据树状图,得到至少有两辆车向右转的结果数,然后利用概率公式求解即可.
【详解】(1)解:画树状图,如图:
由图知,一共有27种等可能的结果,其中两辆车向左转,一辆向右转的结果有3种,
∴两辆车向左转,一辆向右转的概率为;
(2)解:由图知,至少有两辆车向右转的结果有7种,
∴至少有两辆车向右转的概率为.
【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.解题的关键是根据题意画出树状图,再由概率=所求情况数与总情况数之比求解.
72.(1)见解析;(2)这个游戏不公平,理由见解析
【分析】(1)根据题意画出树状图进行求解即可;
(2)根据(1)所画树状图,先得到所有的等可能性的结果数,然后分别得到小球标号之和为奇数和偶数的结果数,最后分别求出甲乙两人赢的概率即可得到答案.
【详解】解:(1)列树状图如下所示:
由树状图可知(m,n)所有可能出现的结果为:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3);
(2)由(1)得一共有9种等可能性的结果数,其中小球上标号之和为奇数的结果数有(1,2),(2,1),(2,3),(3,2),4种等可能性的结果数,其中小球上标号之和为偶数的结果数有(1,1),(1,3),(2,2),(3,1),(3,3),5种等可能性的结果数,
∴甲赢的概率为,乙赢的概率为,
∴这个游戏不公平.
【点睛】本题主要考查了画树状图和游戏的公平性,解题的关键在于能够熟练掌握画树状图的方法.
73.(1)
(2)
【分析】(1)由题意知,摸到红球的概率为;
(2)由题意画树状图,根据树状图求解即可.
【详解】(1)解:由题意知,摸到红球的概率为
∴摸到红球的概率为.
(2)解:由题意画树状图为:
由图可知,两次摸到绿球的概率为
∴两次摸到绿球的概率为.
【点睛】本题考查了树状图求概率.解题的关键在画出于正确的树状图.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
