湘教版(2024)九年级下册1.4 二次函数与一元二次方程的联系 教案(表格式)
文档属性
| 名称 | 湘教版(2024)九年级下册1.4 二次函数与一元二次方程的联系 教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 91.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-02 00:00:00 | ||
图片预览


文档简介
课题:1.4 二次函数与一元二次方程的联系
教学目标 1.能从函数(数与形)角度理解一元二次方程,构建发展互相联系的知识体系; 2.理解一元二次方程根的情况与抛物线y=和直线交点情况之间的联系,能够应用二次函数图像解决有关一元二次方程根的问题; 3.通过二次函数与一元二次方程之间关系的探究,使学生体会数形结合思想,激发学习数学的兴趣。 【重难点】正确理解抛物线与x轴的位置关系与一元二次方程的根的关系.
教学流程及教学内容 教学行为提示及方法指导
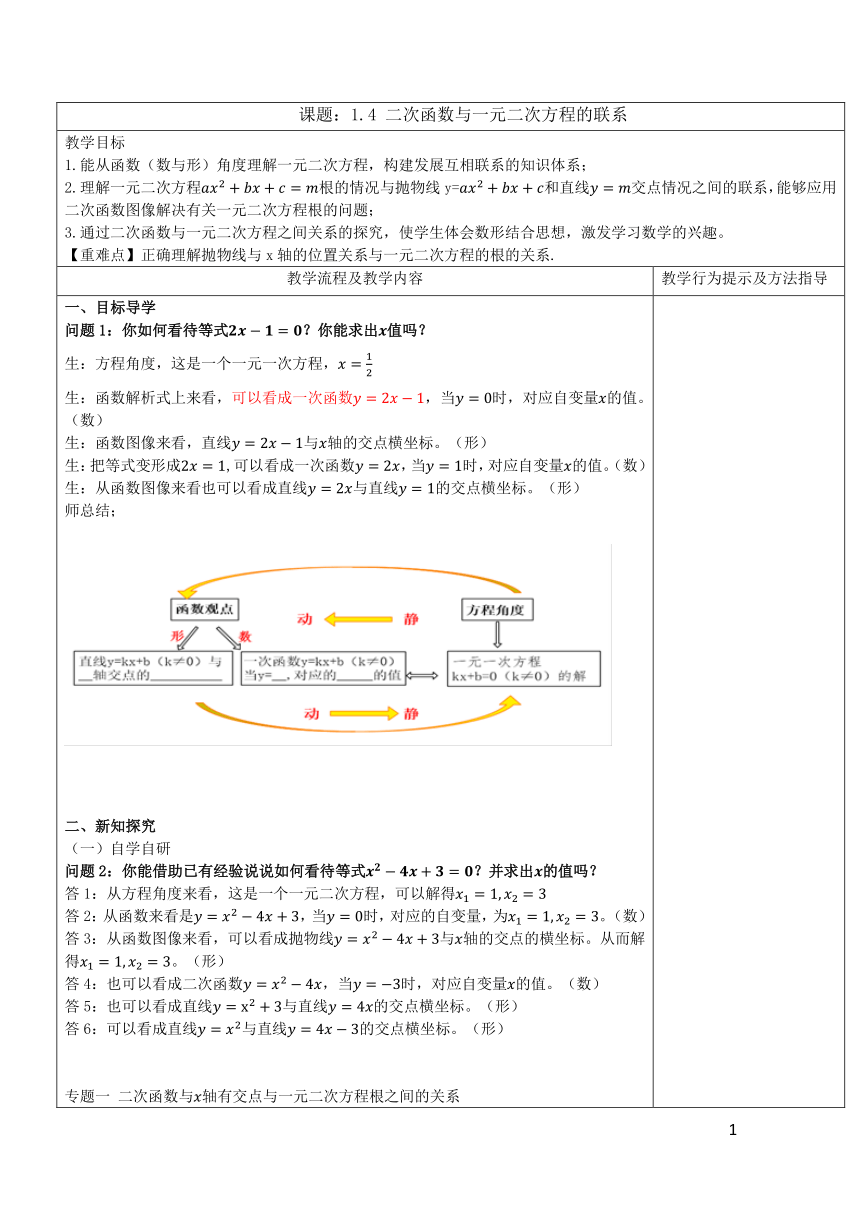
一、目标导学 问题1:你如何看待等式?你能求出值吗? 生:方程角度,这是一个一元一次方程, 生:函数解析式上来看,可以看成一次函数,当时,对应自变量的值。(数) 生:函数图像来看,直线与轴的交点横坐标。(形) 生:把等式变形成,可以看成一次函数,当时,对应自变量的值。(数) 生:从函数图像来看也可以看成直线与直线的交点横坐标。(形) 师总结; 二、新知探究 (一)自学自研 问题2:你能借助已有经验说说如何看待等式?并求出的值吗? 答1:从方程角度来看,这是一个一元二次方程,可以解得 答2:从函数来看是,当时,对应的自变量,为。(数) 答3:从函数图像来看,可以看成抛物线与轴的交点的横坐标。从而解得。(形) 答4:也可以看成二次函数,当时,对应自变量的值。(数) 答5:也可以看成直线与直线的交点横坐标。(形) 答6:可以看成直线与直线的交点横坐标。(形) 专题一 二次函数与轴有交点与一元二次方程根之间的关系 师:刚刚我们也是从函数的观点去看一元二次方程,无论哪一种方法去看,他们都与同一个一元二次方程有关联。 结论1 若一元二次方程的两个根是,则抛物线与轴的两个交点坐标分别是A( , ),B( , )。 结论2 抛物线()与轴的交点的横坐标是一元二次方程的根。 结论3 抛物线y=()与轴的交点的数量是一元二次方程的根的个数。 专题二 抛物线与直线的交点与一元二次方程的根的关系 请你尝试给二次函数的函数值取不同实数时,自变量的取值有何变化。(有难度。合作探究) 生:取,则,这就变成了一元二次方程, 方程可化为: (1)当,即时,方程有两个相等的实数根。 (2)当,即时,方程有两个不相等的实数根。 (比如取时,方程,。) (3)当,即时,方程无实数根。 (比如取时,方程, 此方程无解) 师:还有别的做法吗? 生:用配方法求出函数最小值为,此时,对应有一个自变量取值; 当函数值,此时,对应有两个自变量取值; 当函数值,此时,无对应自变量。 生:借助图像,抛物线与有一个的交点; 与有两个不同的交点; 与无交点。 师:刚刚三位同学从方程角度以及函数数形结合角度分析再进行赋值,说明学数学要先思考策略,然后动手操作。根据刚才这部分的学习,我们发现抛物线与直线的交点个数与一元二次方程的根的个数有紧密联系。 问题1:什么时候二次函数可以转化成一元二次方程? 问题2:当函数赋不同值时,自变量的个数与相应的一元二次方程根的个数有什么关系? 问题3:如何利用图像来确定一元二次方程的根。 问题4:给定一个二次函数值,都会得到一个一元二次方程,如果方程有根,这些方程的根之间有什么关系?为什么? 生:值为一个定值时,二次函数就变成了一元二次方程。 生:自变量的个数与一元二次方程根的个数是相对应的。 生:给定一个函数值,对用到图像上就是纵坐标,点的横坐标就是对应一元二次方程的根。 小结: 结论2二次函数y=的图像与x轴交点的横坐标与一元二次方程根的关系。 二次函数y=的图像与x轴交点个数一元二次方程的根的根的判别式对称轴
(二)合作共研 1.生生交流“自学自研”的内容 2.请学生汇报交流后的结果,老师适时的点评、点拨。 巩固提升 1.二次函数的图象如图,则关于的方程的解是_ _ . 2.方程的根可以看作是: (1)抛物线与直线__ 交点横坐标. (2)抛物线与直线__ 交点横坐标. (3)抛物线与直线__ 交点横坐标. (4)抛物线与直线__ 交点横坐标. (5)抛物线与抛物线__ 交点横坐标. 3.已知二次函数y=x2-2mx+m2+3(m是常数). (1)求证:不论m为何值,该函数的图象与x轴没有公共点; (2)把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点? 我的拙见 为什么改变教材中知识的呈现方式: 首先探究二次函数图像与x轴有两个不同的交点,对应的一元二次方程有两个不相等的解且为()(),然后探究二次函数图像与X轴的位置关系,第三得出用图像法解二次函数近似值,第四探究通过铅球球飞行的实际问题的解决让学生,突出体现了二次函数与实际生活的联系,体会二次函数与一元二次方程的联系。一个是课堂容量太大了,第二在解决实际问题时,学生有可能把关注点放在解决问题上,而忽略了最重要的的内容对二次函数与一元二次方程的联系的本质理解,再者,感觉分两部分研究,不能体现函数思维的由数到形、由形到数的浑然一体。
1
1
教学目标 1.能从函数(数与形)角度理解一元二次方程,构建发展互相联系的知识体系; 2.理解一元二次方程根的情况与抛物线y=和直线交点情况之间的联系,能够应用二次函数图像解决有关一元二次方程根的问题; 3.通过二次函数与一元二次方程之间关系的探究,使学生体会数形结合思想,激发学习数学的兴趣。 【重难点】正确理解抛物线与x轴的位置关系与一元二次方程的根的关系.
教学流程及教学内容 教学行为提示及方法指导
一、目标导学 问题1:你如何看待等式?你能求出值吗? 生:方程角度,这是一个一元一次方程, 生:函数解析式上来看,可以看成一次函数,当时,对应自变量的值。(数) 生:函数图像来看,直线与轴的交点横坐标。(形) 生:把等式变形成,可以看成一次函数,当时,对应自变量的值。(数) 生:从函数图像来看也可以看成直线与直线的交点横坐标。(形) 师总结; 二、新知探究 (一)自学自研 问题2:你能借助已有经验说说如何看待等式?并求出的值吗? 答1:从方程角度来看,这是一个一元二次方程,可以解得 答2:从函数来看是,当时,对应的自变量,为。(数) 答3:从函数图像来看,可以看成抛物线与轴的交点的横坐标。从而解得。(形) 答4:也可以看成二次函数,当时,对应自变量的值。(数) 答5:也可以看成直线与直线的交点横坐标。(形) 答6:可以看成直线与直线的交点横坐标。(形) 专题一 二次函数与轴有交点与一元二次方程根之间的关系 师:刚刚我们也是从函数的观点去看一元二次方程,无论哪一种方法去看,他们都与同一个一元二次方程有关联。 结论1 若一元二次方程的两个根是,则抛物线与轴的两个交点坐标分别是A( , ),B( , )。 结论2 抛物线()与轴的交点的横坐标是一元二次方程的根。 结论3 抛物线y=()与轴的交点的数量是一元二次方程的根的个数。 专题二 抛物线与直线的交点与一元二次方程的根的关系 请你尝试给二次函数的函数值取不同实数时,自变量的取值有何变化。(有难度。合作探究) 生:取,则,这就变成了一元二次方程, 方程可化为: (1)当,即时,方程有两个相等的实数根。 (2)当,即时,方程有两个不相等的实数根。 (比如取时,方程,。) (3)当,即时,方程无实数根。 (比如取时,方程, 此方程无解) 师:还有别的做法吗? 生:用配方法求出函数最小值为,此时,对应有一个自变量取值; 当函数值,此时,对应有两个自变量取值; 当函数值,此时,无对应自变量。 生:借助图像,抛物线与有一个的交点; 与有两个不同的交点; 与无交点。 师:刚刚三位同学从方程角度以及函数数形结合角度分析再进行赋值,说明学数学要先思考策略,然后动手操作。根据刚才这部分的学习,我们发现抛物线与直线的交点个数与一元二次方程的根的个数有紧密联系。 问题1:什么时候二次函数可以转化成一元二次方程? 问题2:当函数赋不同值时,自变量的个数与相应的一元二次方程根的个数有什么关系? 问题3:如何利用图像来确定一元二次方程的根。 问题4:给定一个二次函数值,都会得到一个一元二次方程,如果方程有根,这些方程的根之间有什么关系?为什么? 生:值为一个定值时,二次函数就变成了一元二次方程。 生:自变量的个数与一元二次方程根的个数是相对应的。 生:给定一个函数值,对用到图像上就是纵坐标,点的横坐标就是对应一元二次方程的根。 小结: 结论2二次函数y=的图像与x轴交点的横坐标与一元二次方程根的关系。 二次函数y=的图像与x轴交点个数一元二次方程的根的根的判别式对称轴
(二)合作共研 1.生生交流“自学自研”的内容 2.请学生汇报交流后的结果,老师适时的点评、点拨。 巩固提升 1.二次函数的图象如图,则关于的方程的解是_ _ . 2.方程的根可以看作是: (1)抛物线与直线__ 交点横坐标. (2)抛物线与直线__ 交点横坐标. (3)抛物线与直线__ 交点横坐标. (4)抛物线与直线__ 交点横坐标. (5)抛物线与抛物线__ 交点横坐标. 3.已知二次函数y=x2-2mx+m2+3(m是常数). (1)求证:不论m为何值,该函数的图象与x轴没有公共点; (2)把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点? 我的拙见 为什么改变教材中知识的呈现方式: 首先探究二次函数图像与x轴有两个不同的交点,对应的一元二次方程有两个不相等的解且为()(),然后探究二次函数图像与X轴的位置关系,第三得出用图像法解二次函数近似值,第四探究通过铅球球飞行的实际问题的解决让学生,突出体现了二次函数与实际生活的联系,体会二次函数与一元二次方程的联系。一个是课堂容量太大了,第二在解决实际问题时,学生有可能把关注点放在解决问题上,而忽略了最重要的的内容对二次函数与一元二次方程的联系的本质理解,再者,感觉分两部分研究,不能体现函数思维的由数到形、由形到数的浑然一体。
1
1
