第1单元长方体和正方体常考易错达标卷(含答案)-数学六年级上册苏教版
文档属性
| 名称 | 第1单元长方体和正方体常考易错达标卷(含答案)-数学六年级上册苏教版 |
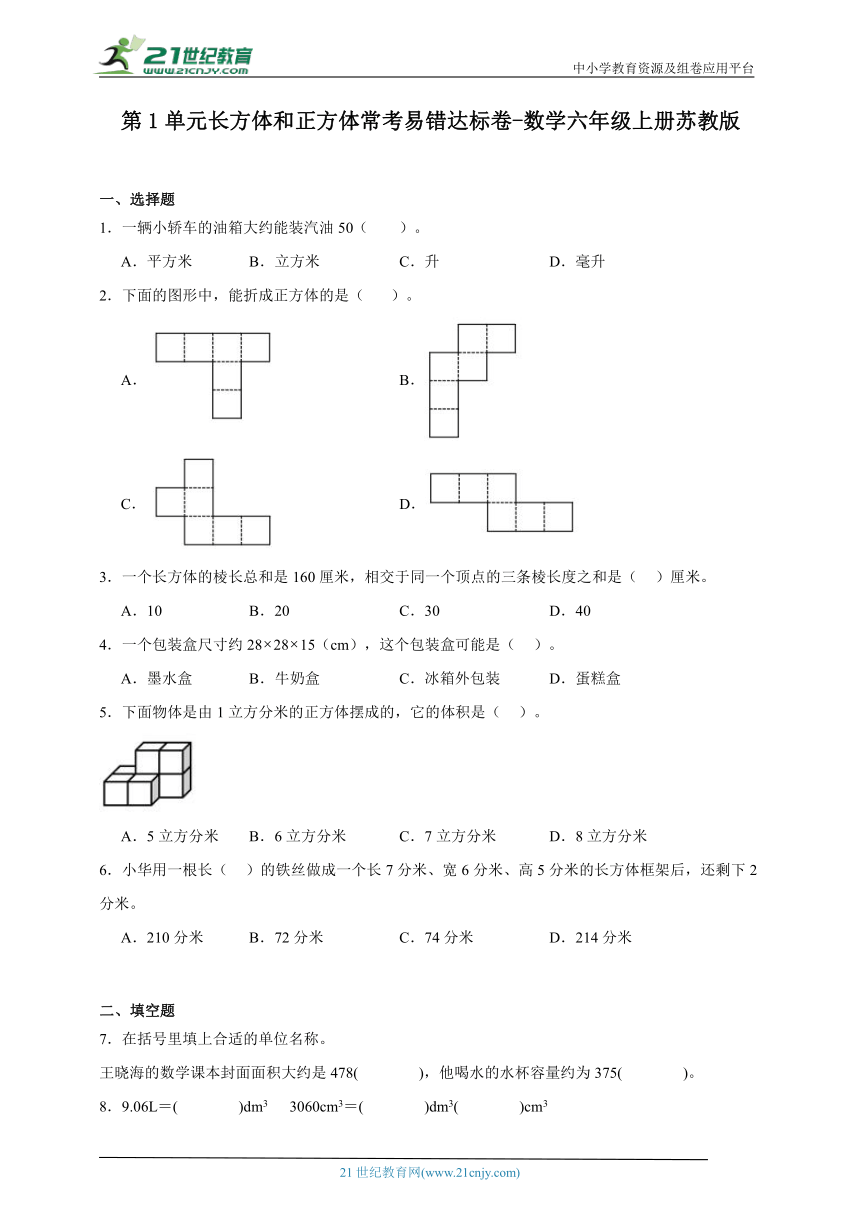
|
|
| 格式 | docx | ||
| 文件大小 | 408.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-03 00:00:00 | ||
图片预览

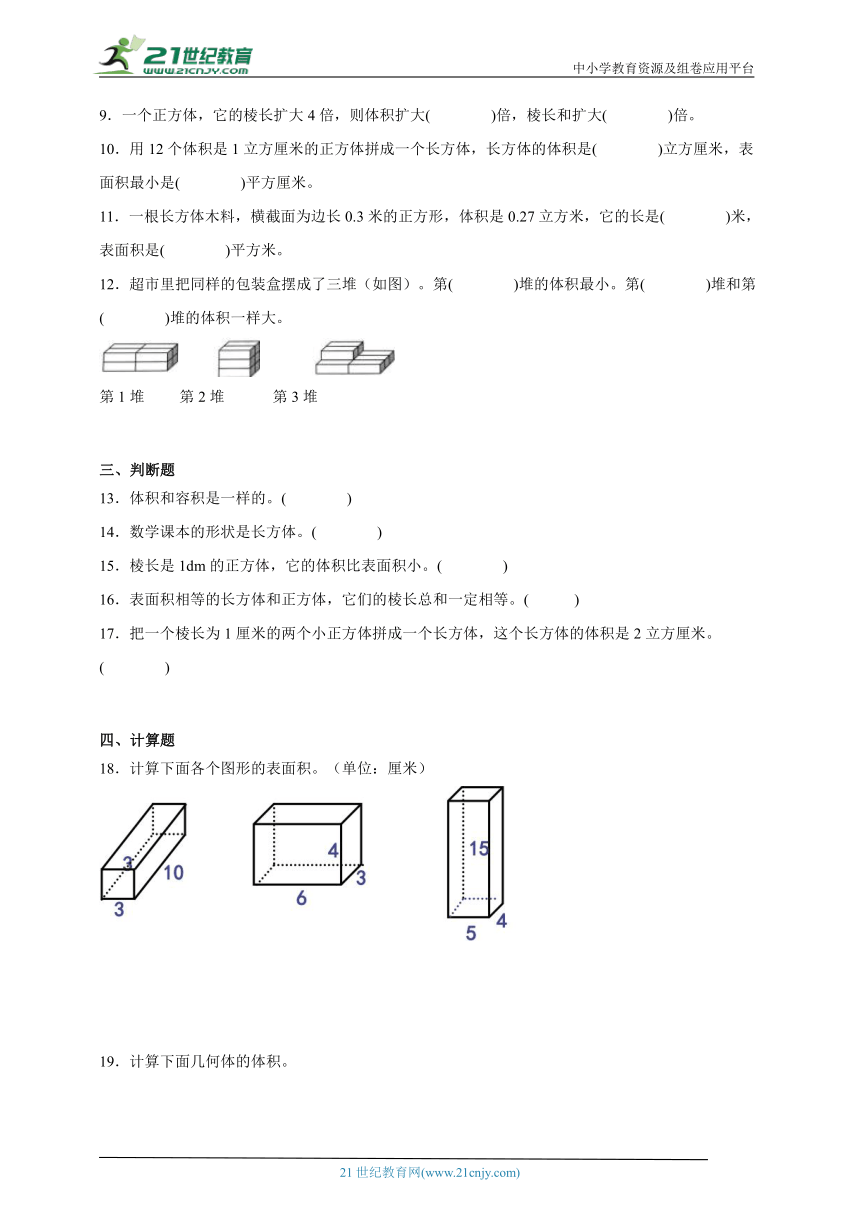
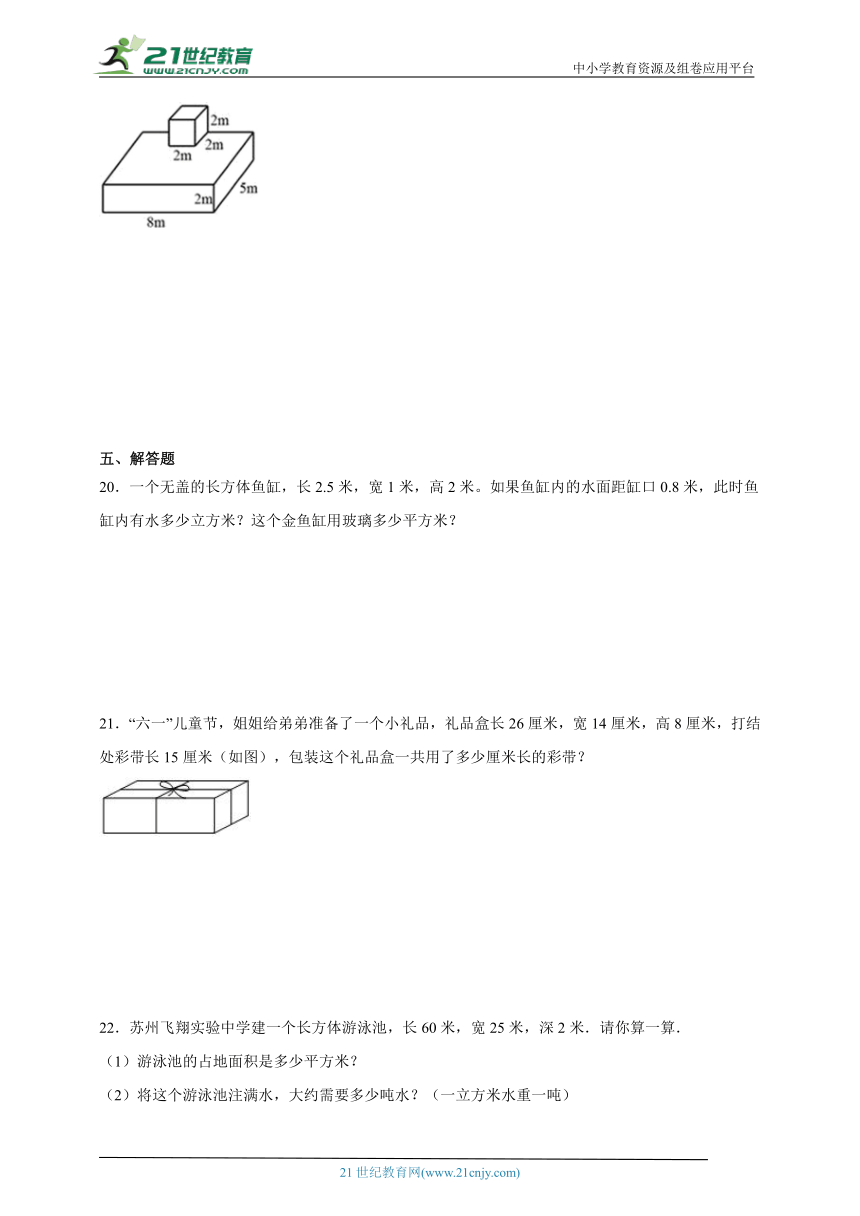


文档简介
中小学教育资源及组卷应用平台
第1单元长方体和正方体常考易错达标卷-数学六年级上册苏教版
一、选择题
1.一辆小轿车的油箱大约能装汽油50( )。
A.平方米 B.立方米 C.升 D.毫升
2.下面的图形中,能折成正方体的是( )。
A. B.
C. D.
3.一个长方体的棱长总和是160厘米,相交于同一个顶点的三条棱长度之和是( )厘米。
A.10 B.20 C.30 D.40
4.一个包装盒尺寸约282815(cm),这个包装盒可能是( )。
A.墨水盒 B.牛奶盒 C.冰箱外包装 D.蛋糕盒
5.下面物体是由1立方分米的正方体摆成的,它的体积是( )。
A.5立方分米 B.6立方分米 C.7立方分米 D.8立方分米
6.小华用一根长( )的铁丝做成一个长7分米、宽6分米、高5分米的长方体框架后,还剩下2分米。
A.210分米 B.72分米 C.74分米 D.214分米
二、填空题
7.在括号里填上合适的单位名称。
王晓海的数学课本封面面积大约是478( ),他喝水的水杯容量约为375( )。
8.9.06L=( )dm3 3060cm3=( )dm3( )cm3
9.一个正方体,它的棱长扩大4倍,则体积扩大( )倍,棱长和扩大( )倍。
10.用12个体积是1立方厘米的正方体拼成一个长方体,长方体的体积是( )立方厘米,表面积最小是( )平方厘米。
11.一根长方体木料,横截面为边长0.3米的正方形,体积是0.27立方米,它的长是( )米,表面积是( )平方米。
12.超市里把同样的包装盒摆成了三堆(如图)。第( )堆的体积最小。第( )堆和第( )堆的体积一样大。
第1堆 第2堆 第3堆
三、判断题
13.体积和容积是一样的。( )
14.数学课本的形状是长方体。( )
15.棱长是1dm的正方体,它的体积比表面积小。( )
16.表面积相等的长方体和正方体,它们的棱长总和一定相等。( )
17.把一个棱长为1厘米的两个小正方体拼成一个长方体,这个长方体的体积是2立方厘米。( )
四、计算题
18.计算下面各个图形的表面积。(单位:厘米)
19.计算下面几何体的体积。
五、解答题
20.一个无盖的长方体鱼缸,长2.5米,宽1米,高2米。如果鱼缸内的水面距缸口0.8米,此时鱼缸内有水多少立方米?这个金鱼缸用玻璃多少平方米?
21.“六一”儿童节,姐姐给弟弟准备了一个小礼品,礼品盒长26厘米,宽14厘米,高8厘米,打结处彩带长15厘米(如图),包装这个礼品盒一共用了多少厘米长的彩带?
22.苏州飞翔实验中学建一个长方体游泳池,长60米,宽25米,深2米.请你算一算.
(1)游泳池的占地面积是多少平方米?
(2)将这个游泳池注满水,大约需要多少吨水?(一立方米水重一吨)
23.把一块棱长是6分米的正方体的钢材,熔铸成长是12分米的长方体钢材。这个长方体钢材的横截面积是多少平方分米?
24.把长40厘米,宽30厘米的长方形铁皮,从四个角各剪去一个边长为5厘米的正方形(如图),再折成一个无盖的长方体铁盒。
(1)如果要给这个长方体铁盒配一个盖子,配这个盖子至少要用多少铁皮?
(2)如果向这个铁盒中注水,水深4厘米,注入水的体积是多少?(铁皮的厚度忽略不计)
参考答案:
1.C
【分析】根据生活经验,计量水、油、饮料等液体的多少,通常用升作单位;可知计量一辆小轿车的油箱应用“升”作单位,约50升。据此判断。
【详解】由分析得:
一辆小轿车的油箱大约能装汽油50升。
故答案为:C
【点睛】解决此类问题注意密切联系生活实际,以及数据的大小来确定计量单位。
2.D
【分析】根据正方体11种展开图,是正方体11种展开图里面的情况能折成正方体,不是正方体展开图的不能折成正方体,据此分析。
【详解】A.不是正方体展开图,不能折成正方体;
B.不是正方体展开图,不能折成正方体;
C.不是正方体展开图,不能折成正方体;
D.3-3型正方体展开图,能折成正方体。
故答案为:D
【点睛】关键是掌握正方体11种展开图,或具有一定的空间想象能力。
3.D
【分析】根据题意可知,相交于同一个顶点的三条棱长之和就是这个长方体的长、宽和高的和;根据长方体棱长总和公式:棱长总和=(长+宽+高)×4;长+宽+高=棱长总和÷4,代入数据,即可解答。
【详解】160÷4=40(厘米)
一个长方体的棱长总和是160厘米,相交于同一个顶点的三条棱长度之和是40厘米。
故答案为:D
【点睛】根据长方体的特征以及长方体棱长总和公式进行解答。
4.D
【分析】根据生活经验以及对数据大小的认识,墨水盒和牛奶盒的包装盒都小,利用28×28×15(cm)的包装盒包装墨水盒牛奶都不合适;冰箱的外包装太大,这个包装太小;因此一个包装盒尺寸约28×28×15(cm),可能是蛋糕盒,据此解答。
【详解】根据分析可知。一个包装盒尺寸约282815(cm),这个包装盒可能是蛋糕盒。
故答案为:D
【点睛】本题考查对体积数据大小的人数以及根据生活经验进行解答。
5.C
【分析】根据题意,一个小正方体的体积是1立方厘米,数出图形中有几个小正方体,体积就是几立方厘米,据此解答。
【详解】有两层,上层有2个小正方体,下层有5个小正方体,一共是2+5=7个小正方体,体积是7立方分米;
故答案为:C。
【点睛】此题主要考查了体积单位的认识,关键是数清楚小正方体的个数,数的时候按照一定的顺序来数,防止多数或漏数。
6.C
【分析】根据长方体棱长总和公式:(长+宽+高)×2,代入数据,求出这个长方体的棱长总和,再加上2分米,就是这根铁丝的长,据此解答。
【详解】(7+6+5)×4+2
=(13+5)×4+2
=18×4+2
=72+2
=74(分米)
故答案选:C
【点睛】本题考查长方体的特征以及长方体棱长总和公式的应用。
7. 平方厘米/cm2 毫升/mL
【分析】根据生活经验、对面积单位、容积单位和数据大小的认识,可知,计量课本封面面积用平方厘米作单位;计量水杯容量用毫升作单位。
【详解】由分析可知:
王晓海的数学课本封面面积大约是478平方厘米,他喝水的水杯容量约为375毫升。
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
8. 9.06 3 60
【分析】1立方分米=1000立方厘米,1立方厘米=1毫升,1升=1000毫升,1立方分米=1升,据此即可求解。
【详解】9.06L=9.06dm3 3060cm3=3dm360cm3
【点睛】此题主要考查体积单位间的进率及单位换算。
9. 64 4
【分析】设正方体的棱长为1,则扩大后的棱长为1×4=4,根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,分别求出扩大后正方体的体积和扩大前正方体的体积,再用扩大后正方体的体积除以扩大前正方体的体积,即可求出体积扩大多少倍;
再根据正方体棱长总和公式:棱长总和=棱长×12,代入数据,求出扩大前和扩大后正方体棱长总和,再用扩大后正方体棱长总和除以扩大前正方体棱长总和,即可求出棱长和扩大多少倍。
【详解】设正方体棱长为1,则扩大后的正方体棱长为:1×4=4。
(4×4×4)÷(1×1×1)
=(16×4)÷(1×1)
=64÷1
=64
(4×12)÷(1×12)
=48÷12
=4
一个正方体,它的棱长扩大4倍,则体积扩大64倍,棱长和扩大4倍。
【点睛】熟练掌握正方体体积公式和棱长总和公式是解答本题的关键。
10. 12 32
【分析】把12个体积是1立方厘米的小正方体拼成一个长方体,要使这个长方体的表面积最小,也就是把12个棱长1厘米的正方体排成长3厘米,宽2厘米,高2厘米的长方体,然后根据长方体的表面积公式S=2(ab+ah+bh),长方体的体积公式V=abh,代入数据解答即可。
【详解】拼成的长方体的长是1×3=3(厘米),宽和高都是1×2=2(厘米)。
3×2×2
=6×2
=12(立方厘米)
(3×2+3×2+2×2)×2
=(6+6+4)×2
=(12+4)×2
=16×2
=32(平方厘米)
这个长方体的体积是12立方厘米,表面积最小是32平方厘米。
【点睛】此题解答关键是理解要使这个长方体的表面积最小,也就是把12个棱长1厘米的正方体排成长3厘米,宽2厘米,高2厘米的长方体,根据长方体的表面积公式和体积公式解答即可。
11. 3 3.78
【分析】根据长方体的体积公式:V=Sh,那么h=V÷S,把数据代入公式求出这根木料的长,再根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式求出它的表面积。
【详解】0.27÷(0.3×0.3)
=0.27÷0.09
=3(米)
(3×0.3+3×0.3+0.3×0.3)×2
=(0.9+0.9+0.09)×2
=1.89×2
=3.78(平方米)
它的长是3米,表面积是3.78平方米。
【点睛】此题主要考查长方体的体积公式、表面积公式的灵活运用,关键是熟记公式。
12. 2 1 3
【分析】根据图片,每堆包装盒都是由小的长方体包装盒组成的,每个小长方体的大小相等,形状相同,所以谁的小包装盒数量多,谁的体积就大,据此数出组成每堆包装盒的小包装盒数量即可。
【详解】由分析可得:
第1堆小包装盒数量:8个;
第2堆小包装盒数量:6个;
第3堆小包装盒数量:8个;
6<8,所以第2堆的体积最小,第1堆和第3堆的体积一样大。
【点睛】本题解题的关键是通过对图片的分析,将体积大小的比较转换到小包装盒的数量比较上,前提条件是所有的小包装盒要完全一样。
13.×
【分析】体积是指物体所占空间的大小,容积是指容器所能容纳物体体积的大小,据此判断。
【详解】由分析可知,体积和容积是不一样的,一般来说,同一个物体的体积大于物体的容积,原题说法错误。
故答案为:×
【点睛】此题考查了对体积、容积的认识,属于基础类题目。
14.√
【分析】根据长方体的特征:长方体有12条棱,6个面,8个顶点;由此可知数学课本有12个棱,6个面,8个顶点,据此解答。
【详解】根据分析可知,数学课本的形状是长方体。
原题干说法正确。
故答案为:√
【点睛】本题考查长方体的特征,根据长方体的特征,进行解答。
15.×
【分析】正方体的体积=棱长×棱长×棱长,正方体的表面积=棱长×棱长×6,据此解答。
【详解】体积:1×1×1=1(立方分米);
表面积:1×1×6=6(平方分米)
体积是1立方分米,表面积是6平方分米,单位不同,无法比较,原题说法错误。
故答案为:×
【点睛】此题考查了正方体体积、表面积的认识,明确体积、表面积不是同一类的量,单位不同,无法比较。
16.×
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,棱长总和=(长+宽+高)×4;正方体的表面积=棱长×棱长×6,棱长总和=棱长×12。此题可以采用举例说明的方法进行判断。
【详解】假设长方体和正方体的表面积都是54平方厘米,则长方体的长、宽、高分别可能是6厘米、3厘米、1厘米,棱长总和=(6+3+1)×4=40(厘米);54=3×3×6,正方体的棱长是3厘米,棱长总和=3×12=36(厘米)。这个长方体和正方体表面积相等,但棱长总和不相等。
故答案为:×
【点睛】此题主要考查正方体、长方体的表面积和棱长总和公式的灵活应用,这类问题可以举例子说明。
17.√
【分析】把棱长为1厘米的两个小正方体拼成一个长方体,则长方体的体积=小正方体的体积×2,据此解答。
【详解】1×1×1×2=2(立方厘米),这个长方体的体积是2立方厘米。
故答案为:√
【点睛】此题考查了立体图形的拼接问题,把较小的立体图形拼成较大的立体图形,其表面积会减少,体积是不变的。
18.138平方厘米;108平方厘米;310平方厘米
【分析】根据长方体表面积公式:(长×宽+宽×高+宽×高)×2,代入数据,即可解答。
【详解】第一个图形表面积:
(3×10+3×3+3×10)×2
=(30+9+30)×2
=(39+30)×2
=69×2
=138(平方厘米)
第二个图形表面积:
(6×3+6×4+3×4)×2
=(18+24+12)×2
=(42+12)×2
=54×2
=108(平方厘米)
第三个图形表面积:
(5×4+5×15+4×15)×2
=(20+75+60)×2
=(95+60)×2
=155×2
=310(平方厘米)
19.88cm3
【分析】这个组合图形的体积等于正方体与长方体的体积和,正方体的体积公式:V=a3,长方体的体积公式:V=abh,把数据代入公式解答。
【详解】2×2×2+8×2×5
=8+80
=88(cm3)
20.3立方米;16.5平方米
【分析】由题意可知,水的高度为(2-0.8)米, 又已知长方体的鱼缸长2.5米,宽1米,根据长方体的体积公式,用2.5×1×(2-0.8)即可求出水的体积;一个无盖的长方体鱼缸表面积只有下、左、右、前、后5个面,据此求出5个面的面积和即可得这个金鱼缸用玻璃多少平方米。
【详解】2.5×1×(2-0.8)
=2.5×1×1.2
=3(立方米)
2.5×1+2.5×2×2+1×2×2
=2.5+10+4
=16.5(平方米)
答:此时鱼缸内有水3立方米;这个金鱼缸用玻璃16.5平方米。
【点睛】本题考查了长方体体积和表面积公式的灵活应用,注意无盖长方体鱼缸表面只有5个面。
21.127厘米
【分析】观察图形可知,捆扎礼品盒的彩带长度=2条长+2条宽+4条高+打结用的15厘米,代入数据计算即可。
【详解】26×2+14×2+8×4+15
=52+28+32+15
=80+32+15
=112+15
=127(厘米)
答:包装这个礼品盒一共用了127厘米长的彩带。
22.(1)1500平方米(2)3000吨
【详解】(1)60×25=1500(平方米)
答:游泳池的占地面积是1500平方米
(2)60×25×2×1=3000(吨)
答:将这个游泳池注满水,大约需要3000吨水
23.18平方分米
【分析】根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,求出正方体体积;由于体积不变,正方体体积=长方体体积;根据长方体体积:体积=底面积×高;底面积=体积÷高;代入数据,即可解答。
【详解】6×6×6÷12
=36×6÷12
=216÷12
=18(平方分米)
答:这个长方体钢材的横截面积是18平方分米。
【点睛】熟练掌握和灵活运用长方体体积公式和正方体体积公式是解答本题的关键。
24.(1)600平方厘米;
(2)2400立方厘米
【分析】(1)由图可知,长方体铁盒的长=长方形铁皮的长-2×小正方形的边长,长方体铁盒的宽=长方形铁皮的宽-2×小正方形的边长,盖子的面积等于长方体的底面积,利用“长方形的面积=长×宽”求出需要铁皮的面积;
(2)根据求出铁盒的长和宽,以及水深4厘米,利用“长方体的体积=长×宽×高”求出注入水的体积,据此解答。
【详解】
(1)长方体铁盒的长:40-5×2
=40-10
=30(厘米)
长方体铁盒的宽:30-5×2
=30-10
=20(厘米)
铁皮的面积:20×30=600(平方厘米)
答:配这个盖子至少要用600平方厘米铁皮。
(2)30×20×4
=600×4
=2400(立方厘米)
答:注入水的体积是2400立方厘米。
【点睛】分析题意求出长方体铁盒的长和宽,并熟记长方体的体积计算公式是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1单元长方体和正方体常考易错达标卷-数学六年级上册苏教版
一、选择题
1.一辆小轿车的油箱大约能装汽油50( )。
A.平方米 B.立方米 C.升 D.毫升
2.下面的图形中,能折成正方体的是( )。
A. B.
C. D.
3.一个长方体的棱长总和是160厘米,相交于同一个顶点的三条棱长度之和是( )厘米。
A.10 B.20 C.30 D.40
4.一个包装盒尺寸约282815(cm),这个包装盒可能是( )。
A.墨水盒 B.牛奶盒 C.冰箱外包装 D.蛋糕盒
5.下面物体是由1立方分米的正方体摆成的,它的体积是( )。
A.5立方分米 B.6立方分米 C.7立方分米 D.8立方分米
6.小华用一根长( )的铁丝做成一个长7分米、宽6分米、高5分米的长方体框架后,还剩下2分米。
A.210分米 B.72分米 C.74分米 D.214分米
二、填空题
7.在括号里填上合适的单位名称。
王晓海的数学课本封面面积大约是478( ),他喝水的水杯容量约为375( )。
8.9.06L=( )dm3 3060cm3=( )dm3( )cm3
9.一个正方体,它的棱长扩大4倍,则体积扩大( )倍,棱长和扩大( )倍。
10.用12个体积是1立方厘米的正方体拼成一个长方体,长方体的体积是( )立方厘米,表面积最小是( )平方厘米。
11.一根长方体木料,横截面为边长0.3米的正方形,体积是0.27立方米,它的长是( )米,表面积是( )平方米。
12.超市里把同样的包装盒摆成了三堆(如图)。第( )堆的体积最小。第( )堆和第( )堆的体积一样大。
第1堆 第2堆 第3堆
三、判断题
13.体积和容积是一样的。( )
14.数学课本的形状是长方体。( )
15.棱长是1dm的正方体,它的体积比表面积小。( )
16.表面积相等的长方体和正方体,它们的棱长总和一定相等。( )
17.把一个棱长为1厘米的两个小正方体拼成一个长方体,这个长方体的体积是2立方厘米。( )
四、计算题
18.计算下面各个图形的表面积。(单位:厘米)
19.计算下面几何体的体积。
五、解答题
20.一个无盖的长方体鱼缸,长2.5米,宽1米,高2米。如果鱼缸内的水面距缸口0.8米,此时鱼缸内有水多少立方米?这个金鱼缸用玻璃多少平方米?
21.“六一”儿童节,姐姐给弟弟准备了一个小礼品,礼品盒长26厘米,宽14厘米,高8厘米,打结处彩带长15厘米(如图),包装这个礼品盒一共用了多少厘米长的彩带?
22.苏州飞翔实验中学建一个长方体游泳池,长60米,宽25米,深2米.请你算一算.
(1)游泳池的占地面积是多少平方米?
(2)将这个游泳池注满水,大约需要多少吨水?(一立方米水重一吨)
23.把一块棱长是6分米的正方体的钢材,熔铸成长是12分米的长方体钢材。这个长方体钢材的横截面积是多少平方分米?
24.把长40厘米,宽30厘米的长方形铁皮,从四个角各剪去一个边长为5厘米的正方形(如图),再折成一个无盖的长方体铁盒。
(1)如果要给这个长方体铁盒配一个盖子,配这个盖子至少要用多少铁皮?
(2)如果向这个铁盒中注水,水深4厘米,注入水的体积是多少?(铁皮的厚度忽略不计)
参考答案:
1.C
【分析】根据生活经验,计量水、油、饮料等液体的多少,通常用升作单位;可知计量一辆小轿车的油箱应用“升”作单位,约50升。据此判断。
【详解】由分析得:
一辆小轿车的油箱大约能装汽油50升。
故答案为:C
【点睛】解决此类问题注意密切联系生活实际,以及数据的大小来确定计量单位。
2.D
【分析】根据正方体11种展开图,是正方体11种展开图里面的情况能折成正方体,不是正方体展开图的不能折成正方体,据此分析。
【详解】A.不是正方体展开图,不能折成正方体;
B.不是正方体展开图,不能折成正方体;
C.不是正方体展开图,不能折成正方体;
D.3-3型正方体展开图,能折成正方体。
故答案为:D
【点睛】关键是掌握正方体11种展开图,或具有一定的空间想象能力。
3.D
【分析】根据题意可知,相交于同一个顶点的三条棱长之和就是这个长方体的长、宽和高的和;根据长方体棱长总和公式:棱长总和=(长+宽+高)×4;长+宽+高=棱长总和÷4,代入数据,即可解答。
【详解】160÷4=40(厘米)
一个长方体的棱长总和是160厘米,相交于同一个顶点的三条棱长度之和是40厘米。
故答案为:D
【点睛】根据长方体的特征以及长方体棱长总和公式进行解答。
4.D
【分析】根据生活经验以及对数据大小的认识,墨水盒和牛奶盒的包装盒都小,利用28×28×15(cm)的包装盒包装墨水盒牛奶都不合适;冰箱的外包装太大,这个包装太小;因此一个包装盒尺寸约28×28×15(cm),可能是蛋糕盒,据此解答。
【详解】根据分析可知。一个包装盒尺寸约282815(cm),这个包装盒可能是蛋糕盒。
故答案为:D
【点睛】本题考查对体积数据大小的人数以及根据生活经验进行解答。
5.C
【分析】根据题意,一个小正方体的体积是1立方厘米,数出图形中有几个小正方体,体积就是几立方厘米,据此解答。
【详解】有两层,上层有2个小正方体,下层有5个小正方体,一共是2+5=7个小正方体,体积是7立方分米;
故答案为:C。
【点睛】此题主要考查了体积单位的认识,关键是数清楚小正方体的个数,数的时候按照一定的顺序来数,防止多数或漏数。
6.C
【分析】根据长方体棱长总和公式:(长+宽+高)×2,代入数据,求出这个长方体的棱长总和,再加上2分米,就是这根铁丝的长,据此解答。
【详解】(7+6+5)×4+2
=(13+5)×4+2
=18×4+2
=72+2
=74(分米)
故答案选:C
【点睛】本题考查长方体的特征以及长方体棱长总和公式的应用。
7. 平方厘米/cm2 毫升/mL
【分析】根据生活经验、对面积单位、容积单位和数据大小的认识,可知,计量课本封面面积用平方厘米作单位;计量水杯容量用毫升作单位。
【详解】由分析可知:
王晓海的数学课本封面面积大约是478平方厘米,他喝水的水杯容量约为375毫升。
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
8. 9.06 3 60
【分析】1立方分米=1000立方厘米,1立方厘米=1毫升,1升=1000毫升,1立方分米=1升,据此即可求解。
【详解】9.06L=9.06dm3 3060cm3=3dm360cm3
【点睛】此题主要考查体积单位间的进率及单位换算。
9. 64 4
【分析】设正方体的棱长为1,则扩大后的棱长为1×4=4,根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,分别求出扩大后正方体的体积和扩大前正方体的体积,再用扩大后正方体的体积除以扩大前正方体的体积,即可求出体积扩大多少倍;
再根据正方体棱长总和公式:棱长总和=棱长×12,代入数据,求出扩大前和扩大后正方体棱长总和,再用扩大后正方体棱长总和除以扩大前正方体棱长总和,即可求出棱长和扩大多少倍。
【详解】设正方体棱长为1,则扩大后的正方体棱长为:1×4=4。
(4×4×4)÷(1×1×1)
=(16×4)÷(1×1)
=64÷1
=64
(4×12)÷(1×12)
=48÷12
=4
一个正方体,它的棱长扩大4倍,则体积扩大64倍,棱长和扩大4倍。
【点睛】熟练掌握正方体体积公式和棱长总和公式是解答本题的关键。
10. 12 32
【分析】把12个体积是1立方厘米的小正方体拼成一个长方体,要使这个长方体的表面积最小,也就是把12个棱长1厘米的正方体排成长3厘米,宽2厘米,高2厘米的长方体,然后根据长方体的表面积公式S=2(ab+ah+bh),长方体的体积公式V=abh,代入数据解答即可。
【详解】拼成的长方体的长是1×3=3(厘米),宽和高都是1×2=2(厘米)。
3×2×2
=6×2
=12(立方厘米)
(3×2+3×2+2×2)×2
=(6+6+4)×2
=(12+4)×2
=16×2
=32(平方厘米)
这个长方体的体积是12立方厘米,表面积最小是32平方厘米。
【点睛】此题解答关键是理解要使这个长方体的表面积最小,也就是把12个棱长1厘米的正方体排成长3厘米,宽2厘米,高2厘米的长方体,根据长方体的表面积公式和体积公式解答即可。
11. 3 3.78
【分析】根据长方体的体积公式:V=Sh,那么h=V÷S,把数据代入公式求出这根木料的长,再根据长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式求出它的表面积。
【详解】0.27÷(0.3×0.3)
=0.27÷0.09
=3(米)
(3×0.3+3×0.3+0.3×0.3)×2
=(0.9+0.9+0.09)×2
=1.89×2
=3.78(平方米)
它的长是3米,表面积是3.78平方米。
【点睛】此题主要考查长方体的体积公式、表面积公式的灵活运用,关键是熟记公式。
12. 2 1 3
【分析】根据图片,每堆包装盒都是由小的长方体包装盒组成的,每个小长方体的大小相等,形状相同,所以谁的小包装盒数量多,谁的体积就大,据此数出组成每堆包装盒的小包装盒数量即可。
【详解】由分析可得:
第1堆小包装盒数量:8个;
第2堆小包装盒数量:6个;
第3堆小包装盒数量:8个;
6<8,所以第2堆的体积最小,第1堆和第3堆的体积一样大。
【点睛】本题解题的关键是通过对图片的分析,将体积大小的比较转换到小包装盒的数量比较上,前提条件是所有的小包装盒要完全一样。
13.×
【分析】体积是指物体所占空间的大小,容积是指容器所能容纳物体体积的大小,据此判断。
【详解】由分析可知,体积和容积是不一样的,一般来说,同一个物体的体积大于物体的容积,原题说法错误。
故答案为:×
【点睛】此题考查了对体积、容积的认识,属于基础类题目。
14.√
【分析】根据长方体的特征:长方体有12条棱,6个面,8个顶点;由此可知数学课本有12个棱,6个面,8个顶点,据此解答。
【详解】根据分析可知,数学课本的形状是长方体。
原题干说法正确。
故答案为:√
【点睛】本题考查长方体的特征,根据长方体的特征,进行解答。
15.×
【分析】正方体的体积=棱长×棱长×棱长,正方体的表面积=棱长×棱长×6,据此解答。
【详解】体积:1×1×1=1(立方分米);
表面积:1×1×6=6(平方分米)
体积是1立方分米,表面积是6平方分米,单位不同,无法比较,原题说法错误。
故答案为:×
【点睛】此题考查了正方体体积、表面积的认识,明确体积、表面积不是同一类的量,单位不同,无法比较。
16.×
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,棱长总和=(长+宽+高)×4;正方体的表面积=棱长×棱长×6,棱长总和=棱长×12。此题可以采用举例说明的方法进行判断。
【详解】假设长方体和正方体的表面积都是54平方厘米,则长方体的长、宽、高分别可能是6厘米、3厘米、1厘米,棱长总和=(6+3+1)×4=40(厘米);54=3×3×6,正方体的棱长是3厘米,棱长总和=3×12=36(厘米)。这个长方体和正方体表面积相等,但棱长总和不相等。
故答案为:×
【点睛】此题主要考查正方体、长方体的表面积和棱长总和公式的灵活应用,这类问题可以举例子说明。
17.√
【分析】把棱长为1厘米的两个小正方体拼成一个长方体,则长方体的体积=小正方体的体积×2,据此解答。
【详解】1×1×1×2=2(立方厘米),这个长方体的体积是2立方厘米。
故答案为:√
【点睛】此题考查了立体图形的拼接问题,把较小的立体图形拼成较大的立体图形,其表面积会减少,体积是不变的。
18.138平方厘米;108平方厘米;310平方厘米
【分析】根据长方体表面积公式:(长×宽+宽×高+宽×高)×2,代入数据,即可解答。
【详解】第一个图形表面积:
(3×10+3×3+3×10)×2
=(30+9+30)×2
=(39+30)×2
=69×2
=138(平方厘米)
第二个图形表面积:
(6×3+6×4+3×4)×2
=(18+24+12)×2
=(42+12)×2
=54×2
=108(平方厘米)
第三个图形表面积:
(5×4+5×15+4×15)×2
=(20+75+60)×2
=(95+60)×2
=155×2
=310(平方厘米)
19.88cm3
【分析】这个组合图形的体积等于正方体与长方体的体积和,正方体的体积公式:V=a3,长方体的体积公式:V=abh,把数据代入公式解答。
【详解】2×2×2+8×2×5
=8+80
=88(cm3)
20.3立方米;16.5平方米
【分析】由题意可知,水的高度为(2-0.8)米, 又已知长方体的鱼缸长2.5米,宽1米,根据长方体的体积公式,用2.5×1×(2-0.8)即可求出水的体积;一个无盖的长方体鱼缸表面积只有下、左、右、前、后5个面,据此求出5个面的面积和即可得这个金鱼缸用玻璃多少平方米。
【详解】2.5×1×(2-0.8)
=2.5×1×1.2
=3(立方米)
2.5×1+2.5×2×2+1×2×2
=2.5+10+4
=16.5(平方米)
答:此时鱼缸内有水3立方米;这个金鱼缸用玻璃16.5平方米。
【点睛】本题考查了长方体体积和表面积公式的灵活应用,注意无盖长方体鱼缸表面只有5个面。
21.127厘米
【分析】观察图形可知,捆扎礼品盒的彩带长度=2条长+2条宽+4条高+打结用的15厘米,代入数据计算即可。
【详解】26×2+14×2+8×4+15
=52+28+32+15
=80+32+15
=112+15
=127(厘米)
答:包装这个礼品盒一共用了127厘米长的彩带。
22.(1)1500平方米(2)3000吨
【详解】(1)60×25=1500(平方米)
答:游泳池的占地面积是1500平方米
(2)60×25×2×1=3000(吨)
答:将这个游泳池注满水,大约需要3000吨水
23.18平方分米
【分析】根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,求出正方体体积;由于体积不变,正方体体积=长方体体积;根据长方体体积:体积=底面积×高;底面积=体积÷高;代入数据,即可解答。
【详解】6×6×6÷12
=36×6÷12
=216÷12
=18(平方分米)
答:这个长方体钢材的横截面积是18平方分米。
【点睛】熟练掌握和灵活运用长方体体积公式和正方体体积公式是解答本题的关键。
24.(1)600平方厘米;
(2)2400立方厘米
【分析】(1)由图可知,长方体铁盒的长=长方形铁皮的长-2×小正方形的边长,长方体铁盒的宽=长方形铁皮的宽-2×小正方形的边长,盖子的面积等于长方体的底面积,利用“长方形的面积=长×宽”求出需要铁皮的面积;
(2)根据求出铁盒的长和宽,以及水深4厘米,利用“长方体的体积=长×宽×高”求出注入水的体积,据此解答。
【详解】
(1)长方体铁盒的长:40-5×2
=40-10
=30(厘米)
长方体铁盒的宽:30-5×2
=30-10
=20(厘米)
铁皮的面积:20×30=600(平方厘米)
答:配这个盖子至少要用600平方厘米铁皮。
(2)30×20×4
=600×4
=2400(立方厘米)
答:注入水的体积是2400立方厘米。
【点睛】分析题意求出长方体铁盒的长和宽,并熟记长方体的体积计算公式是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
