人教A版(2019)必修第二册 6.4.3.1 余弦定理 课件(共20张PPT)
文档属性
| 名称 | 人教A版(2019)必修第二册 6.4.3.1 余弦定理 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-03 15:54:53 | ||
图片预览








文档简介
(共20张PPT)
6.4.3余弦定理、正弦定理
1. 余弦定理
引 入
我们知道,一个三角形含有各种各样的几何量,比如:
三边的边长,三个内角的度数,三角形的面积等.
它们之间应该是存在确定关系的,如
在直角三角形中,边、角之间的定量关系就有勾股定理,锐角三角函数等.
在一般三角形中,我们曾定性地研究过三角形的边角关系,并得到了判定三角形全等的一些方法,如
SSS,SAS,ASA,AAS
这些判定方法表明:给定一个三角形三条边、三个角这6个元素中的某些元素,这个三角形就能唯一确定.
那么三角形的其它元素与这些给定元素之间在数量上到底有着怎样的关系呢,这就是这一部分内容要研究的问题。
在全等三角形的判定中,有一种方法叫SAS(边角边), 即
一个三角形,只要给出了两边及其夹角,这个三角形就唯一确定了,也就是说,这个三角形的其它边和角都可用给出的两边及其夹角计算出来.
知识探究
几何图形到向量
恰当的向量运算
向量到几何关系
返回
余弦定理的内容
三角形中,任何一边的平方,等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍,即
思考(3): 这些结论有何特点,用自然语言该怎样叙述?
问题2: 这你还有证明这个定理的其它思路吗,能把它们现刚才的向量法比较一下吗?
返回
以CB 所在的直线为x 轴,过C点垂直于CB 的直线为y 轴,建立如图所示的坐标系,则有
返回
返回
这三种方法中,用向量法最为简洁,将取两边对应向量为基底,将另一边表示出来,用数量积运算即得结果;
用几何法较为繁琐,要涉及作垂线,需将分锐角、钝角、直三种情况进行讨论,最后进行整合.
返回
思考(3): 由几何法的证明过程,你能得出勾股定理和余弦定理的关系吗?
勾股定理是余弦定理的特例(当两边的夹角为直角时),
余弦定理是勾股定理的推广(把两边的夹角由直角推广到(0°,180°)内的任意角)
问题3: 余弦定理解决了 “ 已知三角两边和夹角,求第三边的问题 ” . 但我们已知了三角形的三边,你能用余弦定理确定三个角的大小吗?
思考(1): 你能用全等三角形的判定方法来解释吗
余弦定理的推论
SSS.
即三角形的三边确定后, 三个角的大小也是确定的.
思考(3): 请再回顾一下余弦定理的相关内容
思考(2): 请你能用自然语言来表述这个结论吗
返回
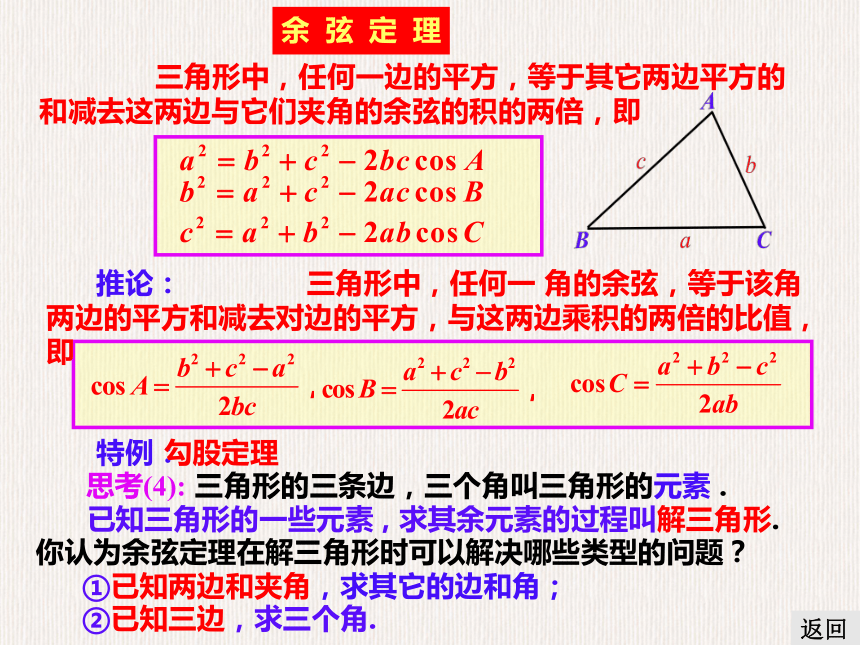
余弦定理
三角形中,任何一边的平方,等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍,即
推论:
特例:
勾股定理
思考(4): 三角形的三条边,三个角叫三角形的元素 .
已知三角形的一些元素 , 求其余元素的过程叫解三角形.
你认为余弦定理在解三角形时可以解决哪些类型的问题?
①已知两边和夹角,求其它的边和角;
②已知三边,求三个角.
三角形中,任何一 角的余弦,等于该角两边的平方和减去对边的平方,与这两边乘积的两倍的比值,即
返回
例析
思考(3): 解三角形,一般是怎样一个思路
先作一个草图,并标出已知元素,
再结合定理,确定恰当求解顺序,
然后依次求余下的元素.
返回
思考: 若去掉题目中 “ 锐角 ”二字,结果会怎样
分两种情况进行讨论:
练习
1.我们是怎样由向量知识得到余弦定理?
课堂小结
余弦定理还有哪些哪些推导方法?你更喜欢哪一种?
坐标法;
几何法.
2.说说余弦定理是怎样的?
其推论是又是怎样的?
3.余弦定理可以直接解决解三角形中的哪些问题?
余弦定理与勾股定理有何关系?
解三角形时我们一般按怎样一个流程进行?
4.有人说,余弦定理还能解决已知两边和一边的对角的这类问题?你以为呢?
课堂小结
6.4.3余弦定理、正弦定理
1. 余弦定理
引 入
我们知道,一个三角形含有各种各样的几何量,比如:
三边的边长,三个内角的度数,三角形的面积等.
它们之间应该是存在确定关系的,如
在直角三角形中,边、角之间的定量关系就有勾股定理,锐角三角函数等.
在一般三角形中,我们曾定性地研究过三角形的边角关系,并得到了判定三角形全等的一些方法,如
SSS,SAS,ASA,AAS
这些判定方法表明:给定一个三角形三条边、三个角这6个元素中的某些元素,这个三角形就能唯一确定.
那么三角形的其它元素与这些给定元素之间在数量上到底有着怎样的关系呢,这就是这一部分内容要研究的问题。
在全等三角形的判定中,有一种方法叫SAS(边角边), 即
一个三角形,只要给出了两边及其夹角,这个三角形就唯一确定了,也就是说,这个三角形的其它边和角都可用给出的两边及其夹角计算出来.
知识探究
几何图形到向量
恰当的向量运算
向量到几何关系
返回
余弦定理的内容
三角形中,任何一边的平方,等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍,即
思考(3): 这些结论有何特点,用自然语言该怎样叙述?
问题2: 这你还有证明这个定理的其它思路吗,能把它们现刚才的向量法比较一下吗?
返回
以CB 所在的直线为x 轴,过C点垂直于CB 的直线为y 轴,建立如图所示的坐标系,则有
返回
返回
这三种方法中,用向量法最为简洁,将取两边对应向量为基底,将另一边表示出来,用数量积运算即得结果;
用几何法较为繁琐,要涉及作垂线,需将分锐角、钝角、直三种情况进行讨论,最后进行整合.
返回
思考(3): 由几何法的证明过程,你能得出勾股定理和余弦定理的关系吗?
勾股定理是余弦定理的特例(当两边的夹角为直角时),
余弦定理是勾股定理的推广(把两边的夹角由直角推广到(0°,180°)内的任意角)
问题3: 余弦定理解决了 “ 已知三角两边和夹角,求第三边的问题 ” . 但我们已知了三角形的三边,你能用余弦定理确定三个角的大小吗?
思考(1): 你能用全等三角形的判定方法来解释吗
余弦定理的推论
SSS.
即三角形的三边确定后, 三个角的大小也是确定的.
思考(3): 请再回顾一下余弦定理的相关内容
思考(2): 请你能用自然语言来表述这个结论吗
返回
余弦定理
三角形中,任何一边的平方,等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍,即
推论:
特例:
勾股定理
思考(4): 三角形的三条边,三个角叫三角形的元素 .
已知三角形的一些元素 , 求其余元素的过程叫解三角形.
你认为余弦定理在解三角形时可以解决哪些类型的问题?
①已知两边和夹角,求其它的边和角;
②已知三边,求三个角.
三角形中,任何一 角的余弦,等于该角两边的平方和减去对边的平方,与这两边乘积的两倍的比值,即
返回
例析
思考(3): 解三角形,一般是怎样一个思路
先作一个草图,并标出已知元素,
再结合定理,确定恰当求解顺序,
然后依次求余下的元素.
返回
思考: 若去掉题目中 “ 锐角 ”二字,结果会怎样
分两种情况进行讨论:
练习
1.我们是怎样由向量知识得到余弦定理?
课堂小结
余弦定理还有哪些哪些推导方法?你更喜欢哪一种?
坐标法;
几何法.
2.说说余弦定理是怎样的?
其推论是又是怎样的?
3.余弦定理可以直接解决解三角形中的哪些问题?
余弦定理与勾股定理有何关系?
解三角形时我们一般按怎样一个流程进行?
4.有人说,余弦定理还能解决已知两边和一边的对角的这类问题?你以为呢?
课堂小结
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
