2024-2025学年人教版八年级数学上册11.1.2 三角形的高、中线与角平分线课件(31张PPT)
文档属性
| 名称 | 2024-2025学年人教版八年级数学上册11.1.2 三角形的高、中线与角平分线课件(31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-03 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
人教版八年级数学上册课件
第十一章 三角形
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
1.理解三角形中线、高线、角平分线等概念.
2.了解三角形重心的概念.
3.会画任意三角形的高、中线与角平分线.运用三角形的高、中线与角平分线的概念进行简单的计算.
一 三角形的高
你还记得 “过一点画已知直线的垂线”吗
你能过三角形的一个顶点,你能画出它的对边的垂线吗
探究新知
如图,线段AD是BC边上的高.
注意:标明垂直的记号和垂足的字母.
B
A
C
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
D
锐角三角形的三条高
每人画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
O
锐角三角形的三条高是在三角形的内部还是外部
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
直角三角形的三条高
在纸上画出一个直角三角形.
A
B
C
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
AB
直角边AB边上的高是______;
CB
(2)它们有怎样的位置关系?
D
斜边AC边上的高是_______.
BD
●
直角三角形的三条高交于直角顶点.
钝角三角形的三条高
(1) 钝角三角形的三条高交于一点吗?
(2)它们所在的直线交于一点吗?
A
B
C
想一想
作钝角△ABC的高
①作BC边上的高,延长CB,过点A作AD BC于D
②作AB边上的高,延长AB,过点C作CE AB于E
③作AC边上的高,过点B作BF AC于F
结论:钝角三角形的三条高不相交于一点.
钝角三角形的三条高所在直线交于一点.
A
B
C
D
E
F
O
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角
三角形
直角
三角形
锐角
三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
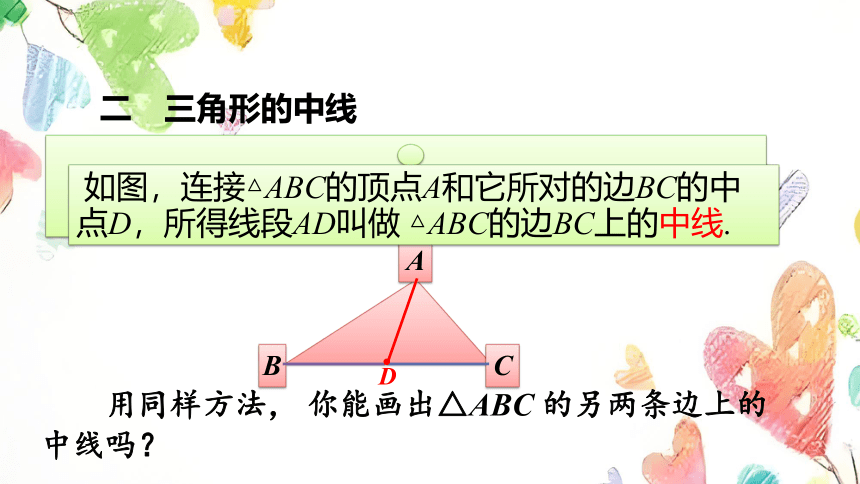
二 三角形的中线
用同样方法, 你能画出△ABC 的另两条边上的中线吗?
B
A
C
D
·
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做 △ABC的边BC上的中线.
如图,三角形的三条中线相交于一点.三角形三
条中线的交点叫做三角形的重心.
B
A
C
D
E
F
·
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
三 三角形的角平分线
如果现在你手上有一张画着一个三角形的薄纸,你能想几种办法画出它的一个内角的平分线?
如图,在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
A
B
C
D
●
●
︶
︶
1
2
因为AD是△ABC的角平分线,
所以∠BAD =∠CAD =
∠BAC.
三角形的三条角平分线相交于一点,交点在三角形的内部.
例1 如图, , , 分别是 的中线、角平分线和高.请你指出图中相等的角及相等的线段.
【点拨】根据三角形的角平分线、中线和高的概念进行解答即可.
重难点拨
【解】 是 的中线, .
是 的角平分线, .
是 的高, .
图中相等的角有: , .
相等的线段有 .
变式 在例1的条件下,小明得出下面五个结论:① ;② ;③ ;④ ;⑤ .其中错误的结论是_____(只填序号).
③
例2 为了美化环境,学校需要在一块三角形空地上种植四种不同的花,并且要求每种花的种植面积相等.请你分别在图1、图2、图3中设计出三种不同的划分方案.
【点拨】先利用三角形的中线把三角形分成面积相等的两个三角形,再继续平分即可得.
【解】答案不唯一.
方案 :如图1,在 边上取点 , ,
F,使 ,连接 , , .
方案 :如图2,分别取 , , 的中点 连接 , , .
方案 :如图3,分别取 , 的中点 , ,再取 的中点 ,连接 , , .
易错示例 下列说法中不正确的是( )
A. 三角形的三条高交于一点 B. 直角三角形有三条高
C. 三角形的三条角平分线交于一点 D. 三角形的三条中线交于一点
【错解】B
A
【点拨】三角形的三条高所在的直线一定交于一点,但三角形的三条高不一定交于一点,比如钝角三角形.
1. 在数学课上,同学们练习画边 上的高时,出现了下列四种图形,其中正确的是( )
A. B. C. D.
C
2. 如图,在 中, , .下列说法中错误的是( )
D
A. 是 的中线
B. 是 的中线
C.
D. 是 的中线
(第2题图)
3. 如图,在 中, , , ,垂足分别为 ,则线段______是 中 边上的高.
(第3题图)
4. 如图,在 中, , , , , 于点 , 为 边上的中线.
(1) 求 与 的周长的差;
解: 为 边上的中线,
.
的周长 的周长 .
(2) 求 的长及 的面积.
解: ,
.
.
.
5. 如图, 为 中 边上一点, , , , 是 边上一点,且 的面积等于 面积的 倍,则 的长为( )
A. B.
C. D.
B
6. 下图是一块三角形的菜地.现要求把这块菜地分成面积比为 的三块,且图中的A处是这三块菜地的公共水源.应该怎样分?
解:如图,在 边上取点 ,使 ,再取 的中点 ,连接 , .
7.(1) 如图, 是 的角平分线, , , 交 于点 .请问: 是 的角平分线吗?如果是,请给予证明;如果不是,请说明理由.
解: 是 的角平分线.
证明: 是 的角平分线,
.
, ,
, .
.
是 的角平分线.
(2) 若将(1)中结论与 是 的角平分线, , 中的任何一个条件交换位置,所得命题正确吗?请直接判断.
所得命题正确.
完成本课课后对应的习题
谢谢欣赏
人教版八年级数学上册课件
第十一章 三角形
11.1 与三角形有关的线段
11.1.2 三角形的高、中线与角平分线
1.理解三角形中线、高线、角平分线等概念.
2.了解三角形重心的概念.
3.会画任意三角形的高、中线与角平分线.运用三角形的高、中线与角平分线的概念进行简单的计算.
一 三角形的高
你还记得 “过一点画已知直线的垂线”吗
你能过三角形的一个顶点,你能画出它的对边的垂线吗
探究新知
如图,线段AD是BC边上的高.
注意:标明垂直的记号和垂足的字母.
B
A
C
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
D
锐角三角形的三条高
每人画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
O
锐角三角形的三条高是在三角形的内部还是外部
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
直角三角形的三条高
在纸上画出一个直角三角形.
A
B
C
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
AB
直角边AB边上的高是______;
CB
(2)它们有怎样的位置关系?
D
斜边AC边上的高是_______.
BD
●
直角三角形的三条高交于直角顶点.
钝角三角形的三条高
(1) 钝角三角形的三条高交于一点吗?
(2)它们所在的直线交于一点吗?
A
B
C
想一想
作钝角△ABC的高
①作BC边上的高,延长CB,过点A作AD BC于D
②作AB边上的高,延长AB,过点C作CE AB于E
③作AC边上的高,过点B作BF AC于F
结论:钝角三角形的三条高不相交于一点.
钝角三角形的三条高所在直线交于一点.
A
B
C
D
E
F
O
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角
三角形
直角
三角形
锐角
三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形
内部
直角顶点
三角形
外部
二 三角形的中线
用同样方法, 你能画出△ABC 的另两条边上的中线吗?
B
A
C
D
·
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做 △ABC的边BC上的中线.
如图,三角形的三条中线相交于一点.三角形三
条中线的交点叫做三角形的重心.
B
A
C
D
E
F
·
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
三 三角形的角平分线
如果现在你手上有一张画着一个三角形的薄纸,你能想几种办法画出它的一个内角的平分线?
如图,在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
A
B
C
D
●
●
︶
︶
1
2
因为AD是△ABC的角平分线,
所以∠BAD =∠CAD =
∠BAC.
三角形的三条角平分线相交于一点,交点在三角形的内部.
例1 如图, , , 分别是 的中线、角平分线和高.请你指出图中相等的角及相等的线段.
【点拨】根据三角形的角平分线、中线和高的概念进行解答即可.
重难点拨
【解】 是 的中线, .
是 的角平分线, .
是 的高, .
图中相等的角有: , .
相等的线段有 .
变式 在例1的条件下,小明得出下面五个结论:① ;② ;③ ;④ ;⑤ .其中错误的结论是_____(只填序号).
③
例2 为了美化环境,学校需要在一块三角形空地上种植四种不同的花,并且要求每种花的种植面积相等.请你分别在图1、图2、图3中设计出三种不同的划分方案.
【点拨】先利用三角形的中线把三角形分成面积相等的两个三角形,再继续平分即可得.
【解】答案不唯一.
方案 :如图1,在 边上取点 , ,
F,使 ,连接 , , .
方案 :如图2,分别取 , , 的中点 连接 , , .
方案 :如图3,分别取 , 的中点 , ,再取 的中点 ,连接 , , .
易错示例 下列说法中不正确的是( )
A. 三角形的三条高交于一点 B. 直角三角形有三条高
C. 三角形的三条角平分线交于一点 D. 三角形的三条中线交于一点
【错解】B
A
【点拨】三角形的三条高所在的直线一定交于一点,但三角形的三条高不一定交于一点,比如钝角三角形.
1. 在数学课上,同学们练习画边 上的高时,出现了下列四种图形,其中正确的是( )
A. B. C. D.
C
2. 如图,在 中, , .下列说法中错误的是( )
D
A. 是 的中线
B. 是 的中线
C.
D. 是 的中线
(第2题图)
3. 如图,在 中, , , ,垂足分别为 ,则线段______是 中 边上的高.
(第3题图)
4. 如图,在 中, , , , , 于点 , 为 边上的中线.
(1) 求 与 的周长的差;
解: 为 边上的中线,
.
的周长 的周长 .
(2) 求 的长及 的面积.
解: ,
.
.
.
5. 如图, 为 中 边上一点, , , , 是 边上一点,且 的面积等于 面积的 倍,则 的长为( )
A. B.
C. D.
B
6. 下图是一块三角形的菜地.现要求把这块菜地分成面积比为 的三块,且图中的A处是这三块菜地的公共水源.应该怎样分?
解:如图,在 边上取点 ,使 ,再取 的中点 ,连接 , .
7.(1) 如图, 是 的角平分线, , , 交 于点 .请问: 是 的角平分线吗?如果是,请给予证明;如果不是,请说明理由.
解: 是 的角平分线.
证明: 是 的角平分线,
.
, ,
, .
.
是 的角平分线.
(2) 若将(1)中结论与 是 的角平分线, , 中的任何一个条件交换位置,所得命题正确吗?请直接判断.
所得命题正确.
完成本课课后对应的习题
谢谢欣赏
