北师大版八年级数学上册 1.2 一定是直角三角形吗 同步测试(含解析)
文档属性
| 名称 | 北师大版八年级数学上册 1.2 一定是直角三角形吗 同步测试(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 565.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-03 20:04:57 | ||
图片预览


文档简介
北师大版八年级数学上册 1.2 一定是直角三角形吗 同步测试
班级: 姓名:
一、单选题
1.若以下列数组为边长,能构成直角三角形的是 ( )
A.4,5,6 B.,,
C.0.2,0.3 ,0.5 D.,,
2.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三个角的度数比为1:2:3 B.三条边的长度比为1:2:3
C.三条边满足关系a2+c2=b2 D.三个角满足关系∠B+∠C=∠A
3.如图, 中, , , , 是 边上的中线,则 的长度为( )
A.1 B.2 C. D.
4.有下列条件:①;②;③;④,其中能确定是直角三角形的是
A.①②④ B.①②③ C.①③④ D.②③④
5.在下列条件:①∠A+∠B=∠C,②∠A:∠B:∠C=3:4:5,③∠C=∠A﹣∠B,④a:b:c=3:4:5中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
6.根据下列条件不能判断△ABC是直角三角形的是( )
A.∠A=55°,∠B=35°
B.∠A:∠B:∠C=7:4:3
C.AB=3,BC=4,CA=
D.AB=m2﹣n2,BC=4mn,AC=m2+n2(m>n>0)
7.如图,已知 中 , , ,在 上取一点E, 上取一点F,使得 ,过点C作 ,交 于点G,过点B作 .则 的度数为( )
A. B. C. D.
8.在正方形网格中画格点 ,如图,若网格中每个小正方形的边长均为 ,则下列说法错误的是( )
A. B. C. D.
9. 中, 、 、 的对边分别为a、b、c,若 ,则有( )
A. B. C. D.
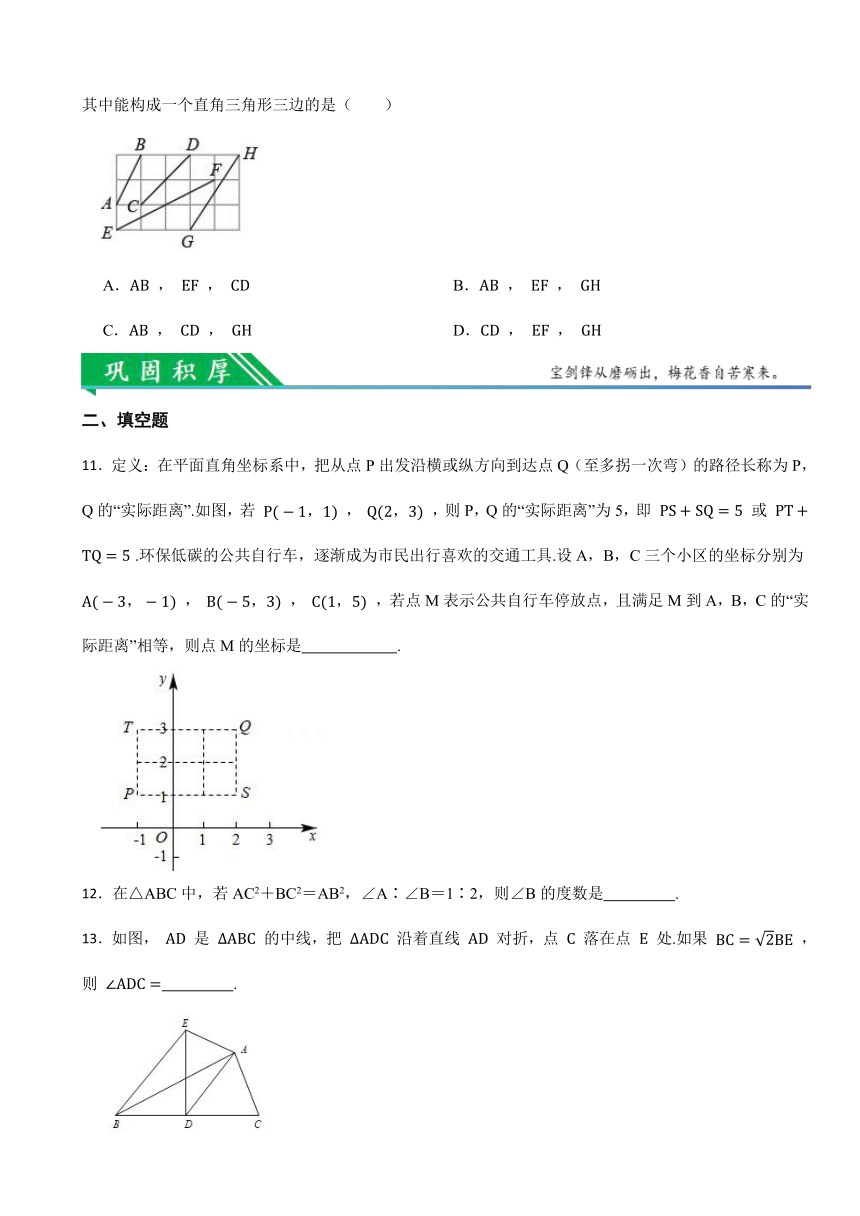
10.如图,由小正方形组成的网格图,每个小正方形的边长均为1,图中标有线段 , , , ,其中能构成一个直角三角形三边的是( )
A. , , B. , ,
C. , , D. , ,
二、填空题
11.定义:在平面直角坐标系中,把从点P出发沿横或纵方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若 , ,则P,Q的“实际距离”为5,即 或 .环保低碳的公共自行车,逐渐成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为 , , ,若点M表示公共自行车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标是 .
12.在△ABC中,若AC2+BC2=AB2,∠A∶∠B=1∶2,则∠B的度数是 .
13.如图, 是 的中线,把 沿着直线 对折,点 落在点 处.如果 ,则 .
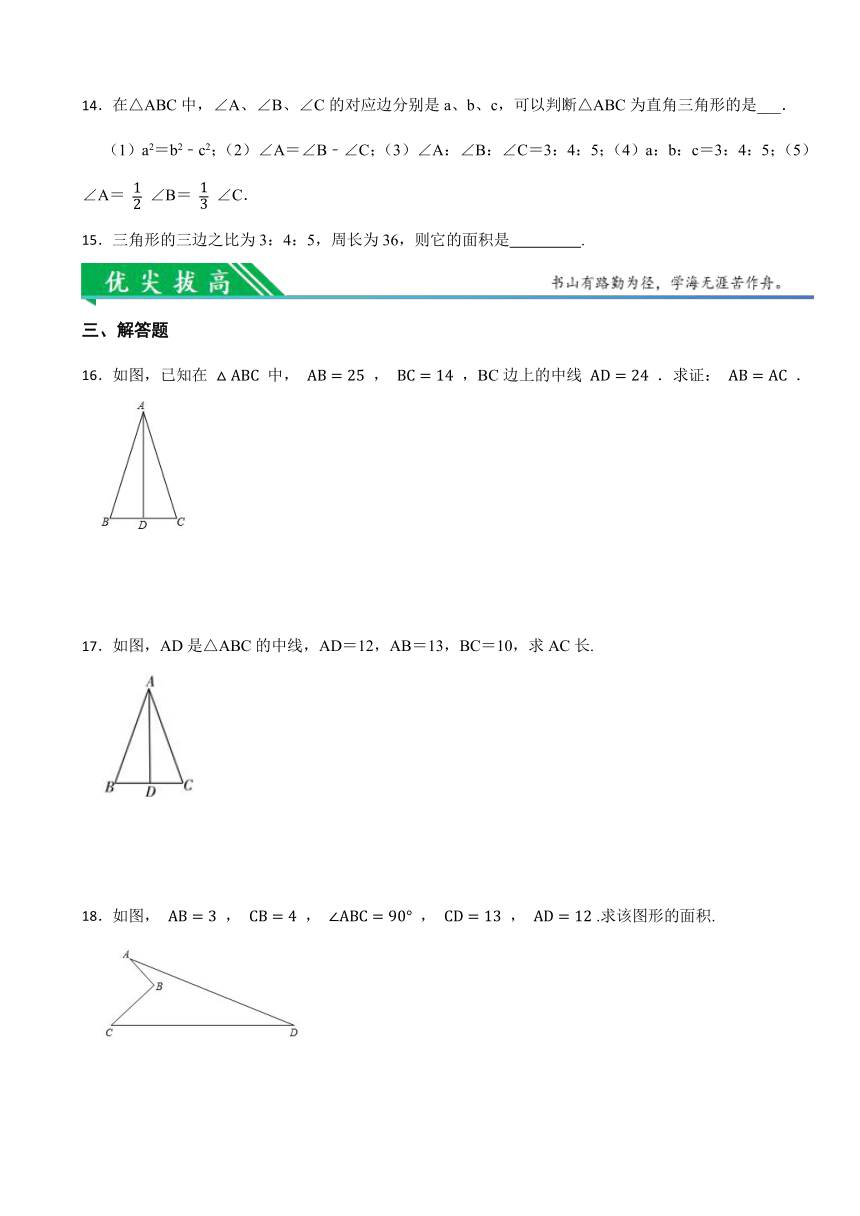
14.在△ABC中,∠A、∠B、∠C的对应边分别是a、b、c,可以判断△ABC为直角三角形的是___.
(1)a2=b2﹣c2;(2)∠A=∠B﹣∠C;(3)∠A:∠B:∠C=3:4:5;(4)a:b:c=3:4:5;(5)∠A= ∠B= ∠C.
15.三角形的三边之比为3:4:5,周长为36,则它的面积是 .
三、解答题
16.如图,已知在 中, , ,BC边上的中线 .求证: .
17.如图,AD是△ABC的中线,AD=12,AB=13,BC=10,求AC长.
18.如图, , , , , .求该图形的面积.
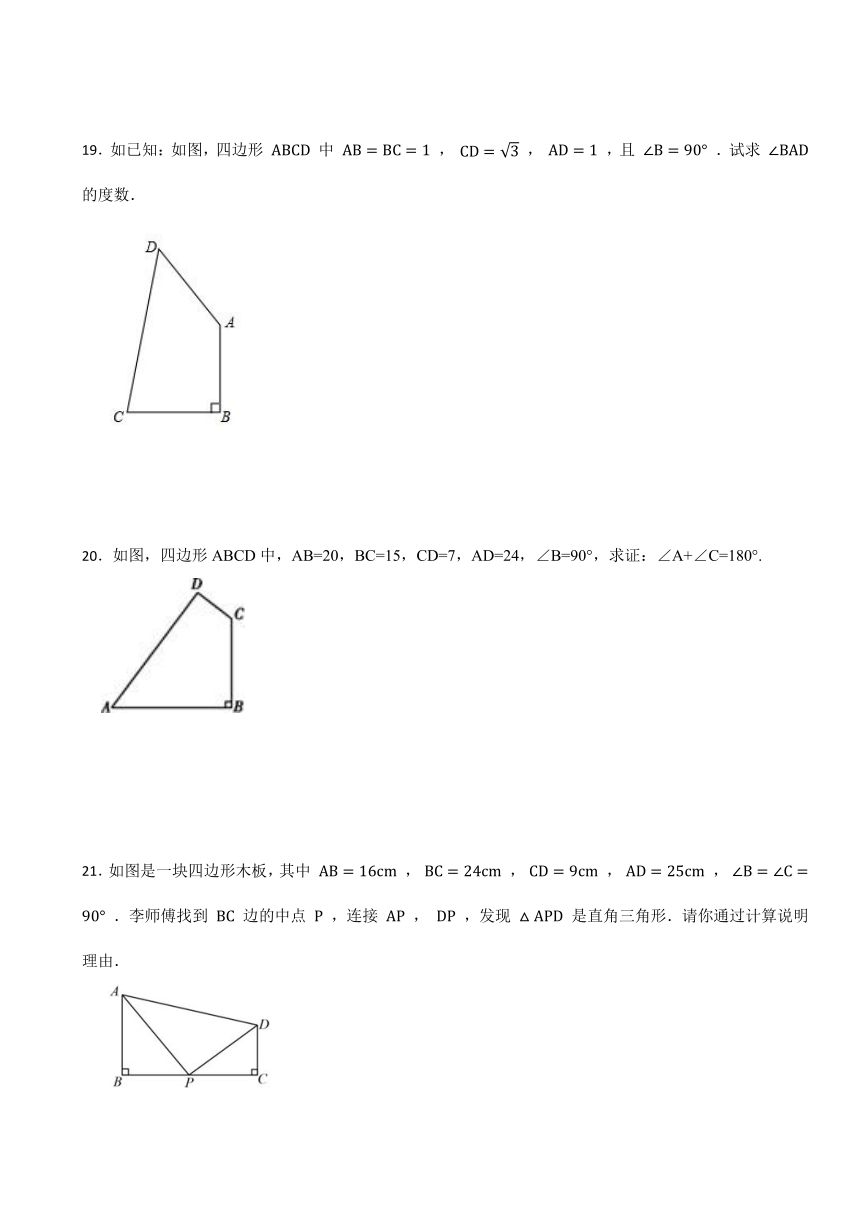
19.如已知:如图,四边形 中 , , ,且 .试求 的度数.
20.如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠A+∠C=180°.
21.如图是一块四边形木板,其中 , , , , .李师傅找到 边的中点 ,连接 , ,发现 是直角三角形.请你通过计算说明理由.
22.如图,甲、乙两船从港口A同时出发,甲船以30海里/时的速度向北偏东35°的方向航行,乙船以40海里/时的速度向另一方向航行,2小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距100海里,则乙船航行的方向是南偏东多少度?
23.如图,在4×4的正方形网格中,每个小正方形的边长都是1.线段AB,AE分别是图中两个1×3的长方形的对角线,请你说明:AB⊥AE.
1.【答案】B
【解析】【解答】解:A、 42+52≠62,不能构成直角三角形;
B、 ()2+()2=()2,能构成直角三角形;
C、 0.22+0.32≠0.52,不能构成直角三角形;
D、 ()2+()2≠()2,不能构成直角三角形.
故答案为:B.
【分析】根据勾股定理的逆定理,只要验证两小边的平方和是否等于最长边的平方即可.
2.【答案】B
【解析】【解答】解:A、三个角的度数比为1:2:3,最大角的度数是90°,是直角三角形,不符合题意;
B、三条边的比为1:2:3,12+22≠32,不是直角三角形,符合题意;
C、三条边满足关系a2+c2=b2,是直角三角形,不符合题意;
D、三个角满足关系∠B+∠C=∠A,所以∠A=90°,是直角三角形,不符合题意;
故答案为:B.
【分析】根据勾股定理的逆定理以及直角三角形的定义判断即可。
3.【答案】D
【解析】【解答】解:∵ , ,
∴ ,
∵ ,
∴ ,
∴ ,
∴△ABC为直角三角形,∠B=90°,
∵ 是 边上的中线,
∴BD= ,
∴ .
故答案为:D
【分析】得出△ABC为直角三角形,∠B=90°,即可得出 的长度。
4.【答案】C
【解析】【解答】解:①由题意知,∵∠A+∠B+∠C=180°,且∠A+∠B=∠C,∴∠C=90°,则△ABC是直角三角形;
②,则△ABC不是直角三角形;
③由题意知,∵∠A+∠B+∠C=180°,且∠A-∠B=∠C,∴∠A=90°,则△ABC是直角三角形;
④由题意知,∵a∶b∶c=3∶4∶5,∴a2+b2=c2=25,则△ABC是直角三角形.
故答案为:C.
【分析】根据内角和定理求出∠C的度数,据此判断①②;根据内角和定理求出∠A的度数,据此判断③;根据勾股定理逆定理可判断④.
5.【答案】C
【解析】【解答】解:①∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴∠C=90°,故△ABC是直角三角形;
②∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,∴∠C=75°,故△ABC不是直角三角形;
③∵∠C=∠A﹣∠B,∠A+∠B+∠C=180°,∴∠B=90°,故△ABC是直角三角形;
④∵a:b:c=3:4:5,∴a2+b2=c2,故△ABC是直角三角形;
故答案为:C.
【分析】根据∠A+∠B=∠C,∠A+∠B+∠C=180°可得∠C=90°,据此判断①;根据∠A:∠B:∠C=3:4:5结合内角和定理求出∠C的度数,据此判断②;由∠C=∠A-∠B结合内角和定理可得∠B=90°,据此判断③;根据勾股定理逆定理可判断④.
6.【答案】D
【解析】【解答】解:A、∵∠A=55°,∠B=35°,
∴∠C=180°﹣55°﹣35°=90°,
∴△ABC是直角三角形;
B、∵∠A:∠B:∠C=7:4:3,
∴∠A=90°,
∴△ABC是直角三角形;
C、∵AB=3,BC=4,CA= ,
∴AB2+CA2=BC2,
∴∠A=90°,
∴△ABC是直角三角形.
D、∵AB=m2﹣n2,BC=4mn,AC=m2+n2,
∴三边长不满足勾股定理的逆定理,
∴△ABC不是直角三角形.
故答案为:D.
【分析】根据三角形的内角和定理求出∠C的度数,据此判断A;根据比的意义结合内角和定理求出∠A的度数,据此判断B;根据勾股定理逆定理可判断C、D.
7.【答案】B
【解析】【解答】解:在△ABC中AC=24,AB=25,BC=7 ,
,
,
△ABC为直角三角形,
∠ACB=90°,
, ,
∠GCF=180°-∠EFC=44°,
∠BCG=∠ACB - ∠GCF=46°,
又 ,
,
∠CBD= ∠BCG= 46°,
故答案为:B.
【分析】利用勾股定理逆定理求出△ABC为直角三角形,然后根据平行线的性质求出∠GCF的度数,再根据角的和差关系求出∠BCG,然后再根据平行线的性质求出∠CBD即可.
8.【答案】C
【解析】【解答】解:由图知: , ,
∵ ,
∴ 是直角三角形,且
∴A、B、D选项正确
故答案为:C
【分析】先勾股勾股定理求出△ABC的各边长,则可判断BCD;再根据勾股定理逆定理判断A,即可解答.
9.【答案】A
【解析】【解答】解: ,
∴ 是直角三角形,且 ,
故答案为:A.
【分析】如果三角形三边长a、b、c满足 ,那么这个三角形是直角三角形,且边a所对的角是直角.
10.【答案】C
【解析】【解答】解:∵由小正方形组成的网格图,每个小正方形的边长均为1
∴ ,
,
,
,
A、 ,故不符合题意;
B、 ,故不符合题意;
C、 ,故符合题意;
D、 ,故不符合题意;
故答案为:C.
【分析】首先根据勾股定理求出AB、CD、EF、GH,然后利用勾股定理逆定理进行判断.
11.【答案】
【解析】【解答】解:设M(x,y),
∵M到A,B,C的“实际距离”相等, , , ,
∴AC实际距离为|1+3|+|5+1|=4+6=10,BC实际距离为|1+5|+|3-1|=6+2=8,
AB实际距离为|-5+3|+|3+1|=2+4=6,
∵62+82=102,
∴△ABC三边的实际距离构成直角三角形,
∴M(x,y)为AC中点,
∴x= ,y= ,
∴CM=|1+1|+|5-2|=2+3=5,BK=|-1+5|+|3-2|=4+1=5,MA=|-1+3|+|2+1|=2+3=5,
∴M(-1,2).
故答案为:(-1,2).
【分析】设M(x,y),则AC=10,BC=8,AB=6,根据勾股定理逆定理可知△ABC为直角三角形,利用中点坐标公式可得点M的坐标,然后求出CM、BK、MA.
12.【答案】60°
【解析】【解答】解:在△ABC中,因为AC2+BC2=AB2,
所以△ABC是以AB为斜边的直角三角形,则∠C=90°,
所以∠A+∠B=90°,
因为∠A:∠B=1:2,
所以∠B=90°×60°.
故答案为:60°.
【分析】根据已知条件结合勾股定理逆定理可得△ABC为直角三角形,且∠C=90°,则∠A+∠B=90°,然后结合∠A∶∠B=1∶2就可求出∠B的度数.
13.【答案】45°
【解析】【解答】解:∵ 是 的中线,把 沿着直线 对折,
∴ , ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
∴△BDE为直角三角形,∠BDE=90°,
∴∠EDC=90°, .
故答案为:45°.
【分析】根据中线以及折叠的性质可得BD=CD=DE,∠ADC=∠ADE,则BD2+DE2=2BD2,结合BC=BE可得BE2=2BD2,则可推出△BDE为直角三角形,且∠BDE=90°,据此解答.
14.【答案】(1)(1)(2)(4)(5)
【解析】【解答】解:∵ 可化为 ,满足勾股定理的逆定理,能够判定 为直角三角形,
故(1)符合题意;
∵ 可化为 ,此时 是直角,能够判定 是直角三角形,
故(2)符合题意;
∵ ,可设 ,则 , ,
∴
∴
∴ , , ,
∴ 不是直角三角形,故(3)不符合题意;
∵ ,可设 ,则 , ,
∴ ,符合勾股定理的逆定理,能够判定 为直角三角形,
故(4)符合题意;
∵ ,
∴ , ,
∴ 是直角三角形,
故(5)符合题意;
综上所述,可以判断 为直角三角形的是:(1)(2)(4)(5);
故答案是:(1)(2)(4)(5).
【分析】根据三角形的内角和及勾股定理逆定理逐项判断即可。
15.【答案】54
【解析】【解答】解:设三角形的三边是3x,4x,5x,
∵(3x)2+(4x)2=(5x)2,
∴此三角形是直角三角形,
∵它的周长是36,
∴3x+4x+5x=36,
∴3x=9,4x=12,
∴三角形的面积= ×9×12=54,
故答案为:54.
【分析】根据勾股定理的逆定理得到三角形是直角三角形,然后根据三角形的面积公式即可得到结论.
16.【答案】证明:∵AD是BC边上的中线
∴
在 中,
∴
∴AD垂直平分BC
∴
【解析】【分析】根据勾股定理的逆定理即可得出答案。
17.【答案】解:∵AD是△ABC的中线,且BC=10,
∴BD= BC=5.
∵52+122=132,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵CD=BD,
∴AC=AB=13.
【解析】【分析】由线段中点定义可得BD=BC,计算BD2、AD2、AB2的值,观察是否满足a2+b2=c2,由勾股定理的逆定理可判断三角形ABD是直角三角形,而CD=BD,根据等腰三角形的三线合一得AB=AC可求解.
18.【答案】解:连接 .
∵在 中, , ,
∴ .
在 中,
∵ ,
∴ 为直角三角形.
∴该图形的面积为 .
【解析】【分析】 连接AC,利用勾股定理求出AC的长,再利用勾股定理的逆定理得出△ADC为直角三角形, 由 该图形的面积为,利用三角形的面积公式计算即得.
19.【答案】解:如图,连接AC
∵ ,
∴ ,∠BAC=45°
又∵ , ,
∴△ACD为直角三角形
∴∠CAD=90°
∴ =135°
【解析】【分析】连接AC,根据勾股定理可得 ,再由勾股定理逆定理可得△ACD为直角三角形,即可求得.
20.【答案】证明:连接AC.
∵AB=20,BC=15,∠B=90°,
∴由勾股定理,得AC2=202+152=625
又CD=7,AD=24,
∴CD2+AD2=625,
∴AC2=CD2+AD2
∴∠D=90°,
∴∠A+∠C=360° 180°=180°
【解析】【分析】连接AC.首先根据勾股定理求得AC的长,再根据勾股定理的逆定理求得∠D=90°,进而求出∠A+∠C=180°
21.【答案】解:∵ 是 的中点,
∴ ,
又∵ ,
∴在 中, ,
在 中, ,
∵在 中, , ,
∴ ,
∴ 是直角三角形.
【解析】【分析】利用勾股定理先求出线段的长度,再利用勾股定理逆定理证明即可。
22.【答案】解:由题意可知,在△ABC中,AC=30×2=60,AB=40×2=80,BC=100,
∴AC2=3600,AB2=6400,BC2=10000,
∴AC2+AB2=BC2,
∴∠CAB=90°,
又∵∠EAD=180°,∠EAC=35°,
∴∠DAB=90°-∠CAE=90°-35°=55°,
∴乙船航行的方向为南偏东55°.
【解析】【分析】由题意可知:在△ABC中,AC=60,AB=80,BC=100,由此可由“勾股定理逆定理”证得∠BAC=90°,结合∠EAD=180°和∠EAC=35°即可求得∠DAB的度数,从而得到乙船的航行方向.
23.【答案】解:如图,连接BE.因为AE2=12+32=10,AB2=12+32=10,BE2=22+42=20,所以AE2+AB2=BE2,所以△ABE是直角三角形,且∠BAE=90°,即AB⊥AE.
【解析】【分析】由勾股定理分别求得AE、AB、BE的值,再证明AE2+AB2=BE2,即可证明AB⊥EA.
班级: 姓名:
一、单选题
1.若以下列数组为边长,能构成直角三角形的是 ( )
A.4,5,6 B.,,
C.0.2,0.3 ,0.5 D.,,
2.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三个角的度数比为1:2:3 B.三条边的长度比为1:2:3
C.三条边满足关系a2+c2=b2 D.三个角满足关系∠B+∠C=∠A
3.如图, 中, , , , 是 边上的中线,则 的长度为( )
A.1 B.2 C. D.
4.有下列条件:①;②;③;④,其中能确定是直角三角形的是
A.①②④ B.①②③ C.①③④ D.②③④
5.在下列条件:①∠A+∠B=∠C,②∠A:∠B:∠C=3:4:5,③∠C=∠A﹣∠B,④a:b:c=3:4:5中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
6.根据下列条件不能判断△ABC是直角三角形的是( )
A.∠A=55°,∠B=35°
B.∠A:∠B:∠C=7:4:3
C.AB=3,BC=4,CA=
D.AB=m2﹣n2,BC=4mn,AC=m2+n2(m>n>0)
7.如图,已知 中 , , ,在 上取一点E, 上取一点F,使得 ,过点C作 ,交 于点G,过点B作 .则 的度数为( )
A. B. C. D.
8.在正方形网格中画格点 ,如图,若网格中每个小正方形的边长均为 ,则下列说法错误的是( )
A. B. C. D.
9. 中, 、 、 的对边分别为a、b、c,若 ,则有( )
A. B. C. D.
10.如图,由小正方形组成的网格图,每个小正方形的边长均为1,图中标有线段 , , , ,其中能构成一个直角三角形三边的是( )
A. , , B. , ,
C. , , D. , ,
二、填空题
11.定义:在平面直角坐标系中,把从点P出发沿横或纵方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若 , ,则P,Q的“实际距离”为5,即 或 .环保低碳的公共自行车,逐渐成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为 , , ,若点M表示公共自行车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标是 .
12.在△ABC中,若AC2+BC2=AB2,∠A∶∠B=1∶2,则∠B的度数是 .
13.如图, 是 的中线,把 沿着直线 对折,点 落在点 处.如果 ,则 .
14.在△ABC中,∠A、∠B、∠C的对应边分别是a、b、c,可以判断△ABC为直角三角形的是___.
(1)a2=b2﹣c2;(2)∠A=∠B﹣∠C;(3)∠A:∠B:∠C=3:4:5;(4)a:b:c=3:4:5;(5)∠A= ∠B= ∠C.
15.三角形的三边之比为3:4:5,周长为36,则它的面积是 .
三、解答题
16.如图,已知在 中, , ,BC边上的中线 .求证: .
17.如图,AD是△ABC的中线,AD=12,AB=13,BC=10,求AC长.
18.如图, , , , , .求该图形的面积.
19.如已知:如图,四边形 中 , , ,且 .试求 的度数.
20.如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠A+∠C=180°.
21.如图是一块四边形木板,其中 , , , , .李师傅找到 边的中点 ,连接 , ,发现 是直角三角形.请你通过计算说明理由.
22.如图,甲、乙两船从港口A同时出发,甲船以30海里/时的速度向北偏东35°的方向航行,乙船以40海里/时的速度向另一方向航行,2小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距100海里,则乙船航行的方向是南偏东多少度?
23.如图,在4×4的正方形网格中,每个小正方形的边长都是1.线段AB,AE分别是图中两个1×3的长方形的对角线,请你说明:AB⊥AE.
1.【答案】B
【解析】【解答】解:A、 42+52≠62,不能构成直角三角形;
B、 ()2+()2=()2,能构成直角三角形;
C、 0.22+0.32≠0.52,不能构成直角三角形;
D、 ()2+()2≠()2,不能构成直角三角形.
故答案为:B.
【分析】根据勾股定理的逆定理,只要验证两小边的平方和是否等于最长边的平方即可.
2.【答案】B
【解析】【解答】解:A、三个角的度数比为1:2:3,最大角的度数是90°,是直角三角形,不符合题意;
B、三条边的比为1:2:3,12+22≠32,不是直角三角形,符合题意;
C、三条边满足关系a2+c2=b2,是直角三角形,不符合题意;
D、三个角满足关系∠B+∠C=∠A,所以∠A=90°,是直角三角形,不符合题意;
故答案为:B.
【分析】根据勾股定理的逆定理以及直角三角形的定义判断即可。
3.【答案】D
【解析】【解答】解:∵ , ,
∴ ,
∵ ,
∴ ,
∴ ,
∴△ABC为直角三角形,∠B=90°,
∵ 是 边上的中线,
∴BD= ,
∴ .
故答案为:D
【分析】得出△ABC为直角三角形,∠B=90°,即可得出 的长度。
4.【答案】C
【解析】【解答】解:①由题意知,∵∠A+∠B+∠C=180°,且∠A+∠B=∠C,∴∠C=90°,则△ABC是直角三角形;
②,则△ABC不是直角三角形;
③由题意知,∵∠A+∠B+∠C=180°,且∠A-∠B=∠C,∴∠A=90°,则△ABC是直角三角形;
④由题意知,∵a∶b∶c=3∶4∶5,∴a2+b2=c2=25,则△ABC是直角三角形.
故答案为:C.
【分析】根据内角和定理求出∠C的度数,据此判断①②;根据内角和定理求出∠A的度数,据此判断③;根据勾股定理逆定理可判断④.
5.【答案】C
【解析】【解答】解:①∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴∠C=90°,故△ABC是直角三角形;
②∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,∴∠C=75°,故△ABC不是直角三角形;
③∵∠C=∠A﹣∠B,∠A+∠B+∠C=180°,∴∠B=90°,故△ABC是直角三角形;
④∵a:b:c=3:4:5,∴a2+b2=c2,故△ABC是直角三角形;
故答案为:C.
【分析】根据∠A+∠B=∠C,∠A+∠B+∠C=180°可得∠C=90°,据此判断①;根据∠A:∠B:∠C=3:4:5结合内角和定理求出∠C的度数,据此判断②;由∠C=∠A-∠B结合内角和定理可得∠B=90°,据此判断③;根据勾股定理逆定理可判断④.
6.【答案】D
【解析】【解答】解:A、∵∠A=55°,∠B=35°,
∴∠C=180°﹣55°﹣35°=90°,
∴△ABC是直角三角形;
B、∵∠A:∠B:∠C=7:4:3,
∴∠A=90°,
∴△ABC是直角三角形;
C、∵AB=3,BC=4,CA= ,
∴AB2+CA2=BC2,
∴∠A=90°,
∴△ABC是直角三角形.
D、∵AB=m2﹣n2,BC=4mn,AC=m2+n2,
∴三边长不满足勾股定理的逆定理,
∴△ABC不是直角三角形.
故答案为:D.
【分析】根据三角形的内角和定理求出∠C的度数,据此判断A;根据比的意义结合内角和定理求出∠A的度数,据此判断B;根据勾股定理逆定理可判断C、D.
7.【答案】B
【解析】【解答】解:在△ABC中AC=24,AB=25,BC=7 ,
,
,
△ABC为直角三角形,
∠ACB=90°,
, ,
∠GCF=180°-∠EFC=44°,
∠BCG=∠ACB - ∠GCF=46°,
又 ,
,
∠CBD= ∠BCG= 46°,
故答案为:B.
【分析】利用勾股定理逆定理求出△ABC为直角三角形,然后根据平行线的性质求出∠GCF的度数,再根据角的和差关系求出∠BCG,然后再根据平行线的性质求出∠CBD即可.
8.【答案】C
【解析】【解答】解:由图知: , ,
∵ ,
∴ 是直角三角形,且
∴A、B、D选项正确
故答案为:C
【分析】先勾股勾股定理求出△ABC的各边长,则可判断BCD;再根据勾股定理逆定理判断A,即可解答.
9.【答案】A
【解析】【解答】解: ,
∴ 是直角三角形,且 ,
故答案为:A.
【分析】如果三角形三边长a、b、c满足 ,那么这个三角形是直角三角形,且边a所对的角是直角.
10.【答案】C
【解析】【解答】解:∵由小正方形组成的网格图,每个小正方形的边长均为1
∴ ,
,
,
,
A、 ,故不符合题意;
B、 ,故不符合题意;
C、 ,故符合题意;
D、 ,故不符合题意;
故答案为:C.
【分析】首先根据勾股定理求出AB、CD、EF、GH,然后利用勾股定理逆定理进行判断.
11.【答案】
【解析】【解答】解:设M(x,y),
∵M到A,B,C的“实际距离”相等, , , ,
∴AC实际距离为|1+3|+|5+1|=4+6=10,BC实际距离为|1+5|+|3-1|=6+2=8,
AB实际距离为|-5+3|+|3+1|=2+4=6,
∵62+82=102,
∴△ABC三边的实际距离构成直角三角形,
∴M(x,y)为AC中点,
∴x= ,y= ,
∴CM=|1+1|+|5-2|=2+3=5,BK=|-1+5|+|3-2|=4+1=5,MA=|-1+3|+|2+1|=2+3=5,
∴M(-1,2).
故答案为:(-1,2).
【分析】设M(x,y),则AC=10,BC=8,AB=6,根据勾股定理逆定理可知△ABC为直角三角形,利用中点坐标公式可得点M的坐标,然后求出CM、BK、MA.
12.【答案】60°
【解析】【解答】解:在△ABC中,因为AC2+BC2=AB2,
所以△ABC是以AB为斜边的直角三角形,则∠C=90°,
所以∠A+∠B=90°,
因为∠A:∠B=1:2,
所以∠B=90°×60°.
故答案为:60°.
【分析】根据已知条件结合勾股定理逆定理可得△ABC为直角三角形,且∠C=90°,则∠A+∠B=90°,然后结合∠A∶∠B=1∶2就可求出∠B的度数.
13.【答案】45°
【解析】【解答】解:∵ 是 的中线,把 沿着直线 对折,
∴ , ,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
∴△BDE为直角三角形,∠BDE=90°,
∴∠EDC=90°, .
故答案为:45°.
【分析】根据中线以及折叠的性质可得BD=CD=DE,∠ADC=∠ADE,则BD2+DE2=2BD2,结合BC=BE可得BE2=2BD2,则可推出△BDE为直角三角形,且∠BDE=90°,据此解答.
14.【答案】(1)(1)(2)(4)(5)
【解析】【解答】解:∵ 可化为 ,满足勾股定理的逆定理,能够判定 为直角三角形,
故(1)符合题意;
∵ 可化为 ,此时 是直角,能够判定 是直角三角形,
故(2)符合题意;
∵ ,可设 ,则 , ,
∴
∴
∴ , , ,
∴ 不是直角三角形,故(3)不符合题意;
∵ ,可设 ,则 , ,
∴ ,符合勾股定理的逆定理,能够判定 为直角三角形,
故(4)符合题意;
∵ ,
∴ , ,
∴ 是直角三角形,
故(5)符合题意;
综上所述,可以判断 为直角三角形的是:(1)(2)(4)(5);
故答案是:(1)(2)(4)(5).
【分析】根据三角形的内角和及勾股定理逆定理逐项判断即可。
15.【答案】54
【解析】【解答】解:设三角形的三边是3x,4x,5x,
∵(3x)2+(4x)2=(5x)2,
∴此三角形是直角三角形,
∵它的周长是36,
∴3x+4x+5x=36,
∴3x=9,4x=12,
∴三角形的面积= ×9×12=54,
故答案为:54.
【分析】根据勾股定理的逆定理得到三角形是直角三角形,然后根据三角形的面积公式即可得到结论.
16.【答案】证明:∵AD是BC边上的中线
∴
在 中,
∴
∴AD垂直平分BC
∴
【解析】【分析】根据勾股定理的逆定理即可得出答案。
17.【答案】解:∵AD是△ABC的中线,且BC=10,
∴BD= BC=5.
∵52+122=132,即BD2+AD2=AB2,
∴△ABD是直角三角形,则AD⊥BC,
又∵CD=BD,
∴AC=AB=13.
【解析】【分析】由线段中点定义可得BD=BC,计算BD2、AD2、AB2的值,观察是否满足a2+b2=c2,由勾股定理的逆定理可判断三角形ABD是直角三角形,而CD=BD,根据等腰三角形的三线合一得AB=AC可求解.
18.【答案】解:连接 .
∵在 中, , ,
∴ .
在 中,
∵ ,
∴ 为直角三角形.
∴该图形的面积为 .
【解析】【分析】 连接AC,利用勾股定理求出AC的长,再利用勾股定理的逆定理得出△ADC为直角三角形, 由 该图形的面积为,利用三角形的面积公式计算即得.
19.【答案】解:如图,连接AC
∵ ,
∴ ,∠BAC=45°
又∵ , ,
∴△ACD为直角三角形
∴∠CAD=90°
∴ =135°
【解析】【分析】连接AC,根据勾股定理可得 ,再由勾股定理逆定理可得△ACD为直角三角形,即可求得.
20.【答案】证明:连接AC.
∵AB=20,BC=15,∠B=90°,
∴由勾股定理,得AC2=202+152=625
又CD=7,AD=24,
∴CD2+AD2=625,
∴AC2=CD2+AD2
∴∠D=90°,
∴∠A+∠C=360° 180°=180°
【解析】【分析】连接AC.首先根据勾股定理求得AC的长,再根据勾股定理的逆定理求得∠D=90°,进而求出∠A+∠C=180°
21.【答案】解:∵ 是 的中点,
∴ ,
又∵ ,
∴在 中, ,
在 中, ,
∵在 中, , ,
∴ ,
∴ 是直角三角形.
【解析】【分析】利用勾股定理先求出线段的长度,再利用勾股定理逆定理证明即可。
22.【答案】解:由题意可知,在△ABC中,AC=30×2=60,AB=40×2=80,BC=100,
∴AC2=3600,AB2=6400,BC2=10000,
∴AC2+AB2=BC2,
∴∠CAB=90°,
又∵∠EAD=180°,∠EAC=35°,
∴∠DAB=90°-∠CAE=90°-35°=55°,
∴乙船航行的方向为南偏东55°.
【解析】【分析】由题意可知:在△ABC中,AC=60,AB=80,BC=100,由此可由“勾股定理逆定理”证得∠BAC=90°,结合∠EAD=180°和∠EAC=35°即可求得∠DAB的度数,从而得到乙船的航行方向.
23.【答案】解:如图,连接BE.因为AE2=12+32=10,AB2=12+32=10,BE2=22+42=20,所以AE2+AB2=BE2,所以△ABE是直角三角形,且∠BAE=90°,即AB⊥AE.
【解析】【分析】由勾股定理分别求得AE、AB、BE的值,再证明AE2+AB2=BE2,即可证明AB⊥EA.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
