2024-2025学年人教版八年级数学上册11.2.1 第2课时 直角三角形的内角性质 课件(共32张PPT)
文档属性
| 名称 | 2024-2025学年人教版八年级数学上册11.2.1 第2课时 直角三角形的内角性质 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-03 19:33:40 | ||
图片预览











文档简介
(共32张PPT)
人教版八年级数学上册课件
第十一章 三角形
11.2 与三角形有关的角
第2课时 直角三角形的内角性质
1.理解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余.
2.掌握有两个角互余的三角形是直角三角形.
3.会运用直角三角形的性质和判定进行相关计算或证明.
合作探究
一 直角三角形两锐角的关系
观察这两个直角三角形,它们两锐角之和分别为多少?
那对于任意直角三角形,这一结论是否还成立呢?
探究新知
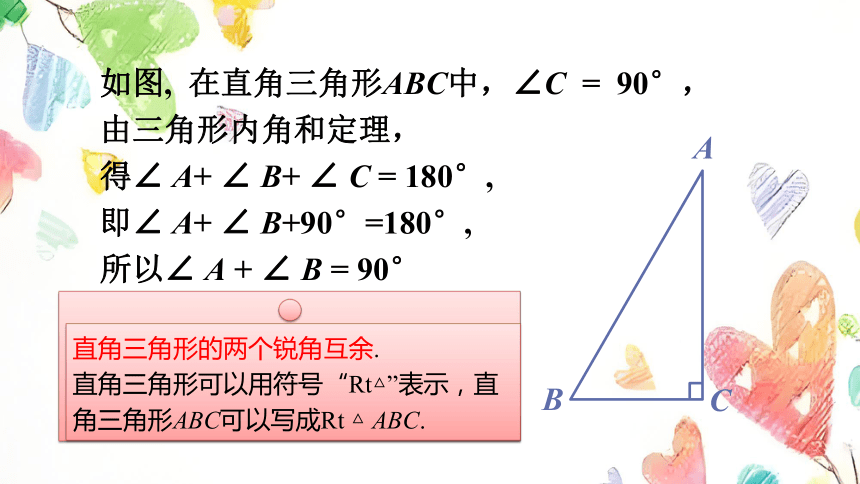
如图, 在直角三角形ABC中,∠C = 90°,
由三角形内角和定理,
得∠ A+ ∠ B+ ∠ C = 180°,
即∠ A+ ∠ B+90°=180°,
所以∠ A + ∠ B = 90°
A
B
C
直角三角形的两个锐角互余.
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成Rt △ ABC.
合作探究
二 直角三角形的判定
我们知道,如果一个三角形是直角三角形,
那么这个三角形有两个角互余.反过来,你能得
出什么结论?这个结论成立吗?如何验证你的想
法?
图是A,B,C三岛的平面图, C岛在A岛的北偏东50°方向,B岛在A岛的北 偏东80°方向,C岛在B岛的北偏西40°方向.从B岛看A,C两岛的视角∠ ABC是多少度?从C岛 看A, B两岛的视角∠ ACB呢?
例2
北
北
C
A
B
D
E
A,B,C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角.如果能求出∠ CAB, ∠ ABC,就能求出∠ ACB.
分析:
解:
∠CAB=∠BAD - ∠CAD=80°-50°=30°.
由 AD//BE,得 ∠ BAD - ∠ ABE=180°.
方法一:
所以
∠ ABE=180° - ∠BAD = 180°- 80°= 100°,
∠ ABC=∠ ABE - ∠EBC=100° - 40°=60°.
在△ABC中,
∠ ACB =180° - ∠ABC - ∠ CAB
= 180° - 60° - 30°=90°.
从B岛看A, C两岛的视角∠ ABC是
60°, 从C岛看A, B两岛的视
角∠ ACB是90°.
答:
你还能想到其他解法吗?
B
D
C
E
北
A
你能想出一个更简捷的方法来求∠C的度数吗?
1
2
50°
40°
F
∵ CF∥AD, 又AD ∥BE,
∴ CF∥ BE,
∴∠2=∠CBE =40 °
∴ ∠ACB=∠1 + ∠2 =50 ° + 40 ° =90 °
解:
北
方法二:
合作探究
二 直角三角形的判定
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,你能得出什么结论?这个结论成立吗?如何验证你的想法?
假设在△ABC中,∠A+∠B=90°,
由三角形内角和定理,我们可以得到∠C=180 ° -( ∠A+∠B)=90°,
即∠C是直角,那么△ABC是直角三角形.
由三角形内角和定理可得:
有两个角互余的三角形是直角三角形.
如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.试说明△EFP为直角三角形.
例3
判断△EFP为直角三角形有两种方法:有一角是
直角或两锐角互余,即要说明∠EPF=90°或
∠EFP+∠FEP=90°.
分析:
∵AB∥CD,∴∠BEF+∠DFE=180°.
∵EP为∠BEF的平分线,FP为∠EFD的平分线,
∴∠PEF= ∠BEF,∠PFE= ∠DFE.
∴∠PEF+∠PFE= (∠BEF+∠DFE)
= ×180°=90°.
∴∠EPF=180°-(∠PEF+∠PFE)=90°.
∴△EFP为直角三角形.
解:
例1 如图, , ,垂足为 .下列结论中错误的是( )
A. 图中有三个直角三角形
B.
C. 和 都是 的余角
D.
B
【点拨】在 中, , ,由此可判断直角三角形的个数,再根据直角三角形两锐角互余,即可得出答案.
重难点拨
变式 如图,在 中, , 是 边上的高.若 ,则 的度数为( )
A. B.
C. D.
A
例2 如图,在 中, , 是 边上一点,且 .求证: 是直角三角形.
【点拨】要证 是直角三角形,可证明 .在 中,已知 , ,至此易得 是直角三角形.
【证明】 ,
.
,
.
.
.
是直角三角形.
变式 有下列条件:① ,② ,③ ,④ .其中能使 是直角三角形的条件有_________(填序号).
①②③
1. 在 中, , ,则 的度数为( )
A. B. C. D.
B
2. 若一个三角形三个内角的度数之比是 ,则此三角形是( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 以上三种都有可能
A
3. 如图,在 中, , , ,则 的度数为 ( )
A. B.
C. D.
C
4. 如图,点 在 的边 的延长线上, 于点E,交 于点F.若 , ,则 的度数为_______.
5. 如图, 于点 , 于点C, 与 相交于点 .
(1) 和 有什么数量关系?请说明理由.
解: .
理由: , ,
, .
.
(2) 若 ,则 和 各是多少度?
,由(1)知 , ,
,
.
.
6. 如图,在 中, ,点 在 上, .若 ,则 的度数为( )
A. B.
C. D.
D
7. 如图,在 中, , , 平分 .
(1) 求 的度数.
解: 中, , ,
.
又 平分 ,
.
(2) 若 于点 , ,求证: 是直角三角形.
证明: , ,
.
又 ,
.
又 ,
.
是直角三角形.
8.(1) 如图1,将一块直角三角板 放置在 上,使三角板 的两条直角边 , 分别经过点 .在 中,若 ,则 _______, ______.
(2) 如图2,在(1)的条件下,改变直角三角板 的位置,使三角板 的两条直角边 , 仍然分别经过点 , ,其他条件不变,那么 的度数是否会发生变化?若会发生变化,请举例说明;若不会发生变化,请求出 的度数.
解:不会发生变化.
, .
, .
.
完成本课课后的习题
谢谢大家欣赏
人教版八年级数学上册课件
第十一章 三角形
11.2 与三角形有关的角
第2课时 直角三角形的内角性质
1.理解直角三角形的概念,探索并掌握直角三角形的性质定理:直角三角形的两个锐角互余.
2.掌握有两个角互余的三角形是直角三角形.
3.会运用直角三角形的性质和判定进行相关计算或证明.
合作探究
一 直角三角形两锐角的关系
观察这两个直角三角形,它们两锐角之和分别为多少?
那对于任意直角三角形,这一结论是否还成立呢?
探究新知
如图, 在直角三角形ABC中,∠C = 90°,
由三角形内角和定理,
得∠ A+ ∠ B+ ∠ C = 180°,
即∠ A+ ∠ B+90°=180°,
所以∠ A + ∠ B = 90°
A
B
C
直角三角形的两个锐角互余.
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成Rt △ ABC.
合作探究
二 直角三角形的判定
我们知道,如果一个三角形是直角三角形,
那么这个三角形有两个角互余.反过来,你能得
出什么结论?这个结论成立吗?如何验证你的想
法?
图是A,B,C三岛的平面图, C岛在A岛的北偏东50°方向,B岛在A岛的北 偏东80°方向,C岛在B岛的北偏西40°方向.从B岛看A,C两岛的视角∠ ABC是多少度?从C岛 看A, B两岛的视角∠ ACB呢?
例2
北
北
C
A
B
D
E
A,B,C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角.如果能求出∠ CAB, ∠ ABC,就能求出∠ ACB.
分析:
解:
∠CAB=∠BAD - ∠CAD=80°-50°=30°.
由 AD//BE,得 ∠ BAD - ∠ ABE=180°.
方法一:
所以
∠ ABE=180° - ∠BAD = 180°- 80°= 100°,
∠ ABC=∠ ABE - ∠EBC=100° - 40°=60°.
在△ABC中,
∠ ACB =180° - ∠ABC - ∠ CAB
= 180° - 60° - 30°=90°.
从B岛看A, C两岛的视角∠ ABC是
60°, 从C岛看A, B两岛的视
角∠ ACB是90°.
答:
你还能想到其他解法吗?
B
D
C
E
北
A
你能想出一个更简捷的方法来求∠C的度数吗?
1
2
50°
40°
F
∵ CF∥AD, 又AD ∥BE,
∴ CF∥ BE,
∴∠2=∠CBE =40 °
∴ ∠ACB=∠1 + ∠2 =50 ° + 40 ° =90 °
解:
北
方法二:
合作探究
二 直角三角形的判定
我们知道,如果一个三角形是直角三角形,那么这个三角形有两个角互余.反过来,你能得出什么结论?这个结论成立吗?如何验证你的想法?
假设在△ABC中,∠A+∠B=90°,
由三角形内角和定理,我们可以得到∠C=180 ° -( ∠A+∠B)=90°,
即∠C是直角,那么△ABC是直角三角形.
由三角形内角和定理可得:
有两个角互余的三角形是直角三角形.
如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.试说明△EFP为直角三角形.
例3
判断△EFP为直角三角形有两种方法:有一角是
直角或两锐角互余,即要说明∠EPF=90°或
∠EFP+∠FEP=90°.
分析:
∵AB∥CD,∴∠BEF+∠DFE=180°.
∵EP为∠BEF的平分线,FP为∠EFD的平分线,
∴∠PEF= ∠BEF,∠PFE= ∠DFE.
∴∠PEF+∠PFE= (∠BEF+∠DFE)
= ×180°=90°.
∴∠EPF=180°-(∠PEF+∠PFE)=90°.
∴△EFP为直角三角形.
解:
例1 如图, , ,垂足为 .下列结论中错误的是( )
A. 图中有三个直角三角形
B.
C. 和 都是 的余角
D.
B
【点拨】在 中, , ,由此可判断直角三角形的个数,再根据直角三角形两锐角互余,即可得出答案.
重难点拨
变式 如图,在 中, , 是 边上的高.若 ,则 的度数为( )
A. B.
C. D.
A
例2 如图,在 中, , 是 边上一点,且 .求证: 是直角三角形.
【点拨】要证 是直角三角形,可证明 .在 中,已知 , ,至此易得 是直角三角形.
【证明】 ,
.
,
.
.
.
是直角三角形.
变式 有下列条件:① ,② ,③ ,④ .其中能使 是直角三角形的条件有_________(填序号).
①②③
1. 在 中, , ,则 的度数为( )
A. B. C. D.
B
2. 若一个三角形三个内角的度数之比是 ,则此三角形是( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 以上三种都有可能
A
3. 如图,在 中, , , ,则 的度数为 ( )
A. B.
C. D.
C
4. 如图,点 在 的边 的延长线上, 于点E,交 于点F.若 , ,则 的度数为_______.
5. 如图, 于点 , 于点C, 与 相交于点 .
(1) 和 有什么数量关系?请说明理由.
解: .
理由: , ,
, .
.
(2) 若 ,则 和 各是多少度?
,由(1)知 , ,
,
.
.
6. 如图,在 中, ,点 在 上, .若 ,则 的度数为( )
A. B.
C. D.
D
7. 如图,在 中, , , 平分 .
(1) 求 的度数.
解: 中, , ,
.
又 平分 ,
.
(2) 若 于点 , ,求证: 是直角三角形.
证明: , ,
.
又 ,
.
又 ,
.
是直角三角形.
8.(1) 如图1,将一块直角三角板 放置在 上,使三角板 的两条直角边 , 分别经过点 .在 中,若 ,则 _______, ______.
(2) 如图2,在(1)的条件下,改变直角三角板 的位置,使三角板 的两条直角边 , 仍然分别经过点 , ,其他条件不变,那么 的度数是否会发生变化?若会发生变化,请举例说明;若不会发生变化,请求出 的度数.
解:不会发生变化.
, .
, .
.
完成本课课后的习题
谢谢大家欣赏
