第二十二章 二次函数 单元测试(含答案)2024-2025学年数学人教版(2012)九年级上册
文档属性
| 名称 | 第二十二章 二次函数 单元测试(含答案)2024-2025学年数学人教版(2012)九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1013.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-03 19:53:30 | ||
图片预览



文档简介
二次函数
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.当函数是二次函数时,a的取值为( )
A. B. C. D.
2.已知A、B是抛物线上关于对称轴对称的两点,若点A的横坐标是,则点B横坐标为( )
A.2 B.3 C.4 D.5
3.二次函数的顶点坐标是( )
A. B. C. D.
4.慈城某店家销售特产印花糕,经调查发现每盒印花糕售价为元时,日销售量为盒,当每盒售价每下降1元时,日销售量会增加5盒.已知每盒印花糕的成本为5元,设每盒降价x元,商家每天的利润为y元,则y与x之间的函数表达式为( )
A. B.
C. D.
5.若二次函数的图象如图所示,则坐标原点可能是( )
A.点P B.点Q C.点M D.点N
6.已知在平面直角坐标系中,抛物线的图象如图所示,对称轴为直线,将抛物线向右平移2个单位长度得到抛物线:(a、b、c为常数,且),则代数式与0的大小关系是( )
A. B. C. D.不能确定
7.已知二次函数,则下列表述正确的是( )
A.若,抛物线的开口向下 B.当时,y随x的增大而增大
C.图象与x轴一定有两个交点 D.图象与y轴的交点坐标为
8.如图所示,是一座抛物线型的拱桥,当桥下水面宽度是时,拱顶到水面的距离是,当水面下降后,水面的宽度是( )m.
A.6 B. C. D.
9.如图,二次函数的部分图象与x轴的一个交点的横坐标是,顶点坐标为,则下列说法正确的是( )
A.二次函数图象的对称轴是直线
B.二次函数图象与x轴的另一个交点的横坐标是2
C.当时,y随x的增大而减小
D.二次函数图象与y轴的交点的纵坐标是3
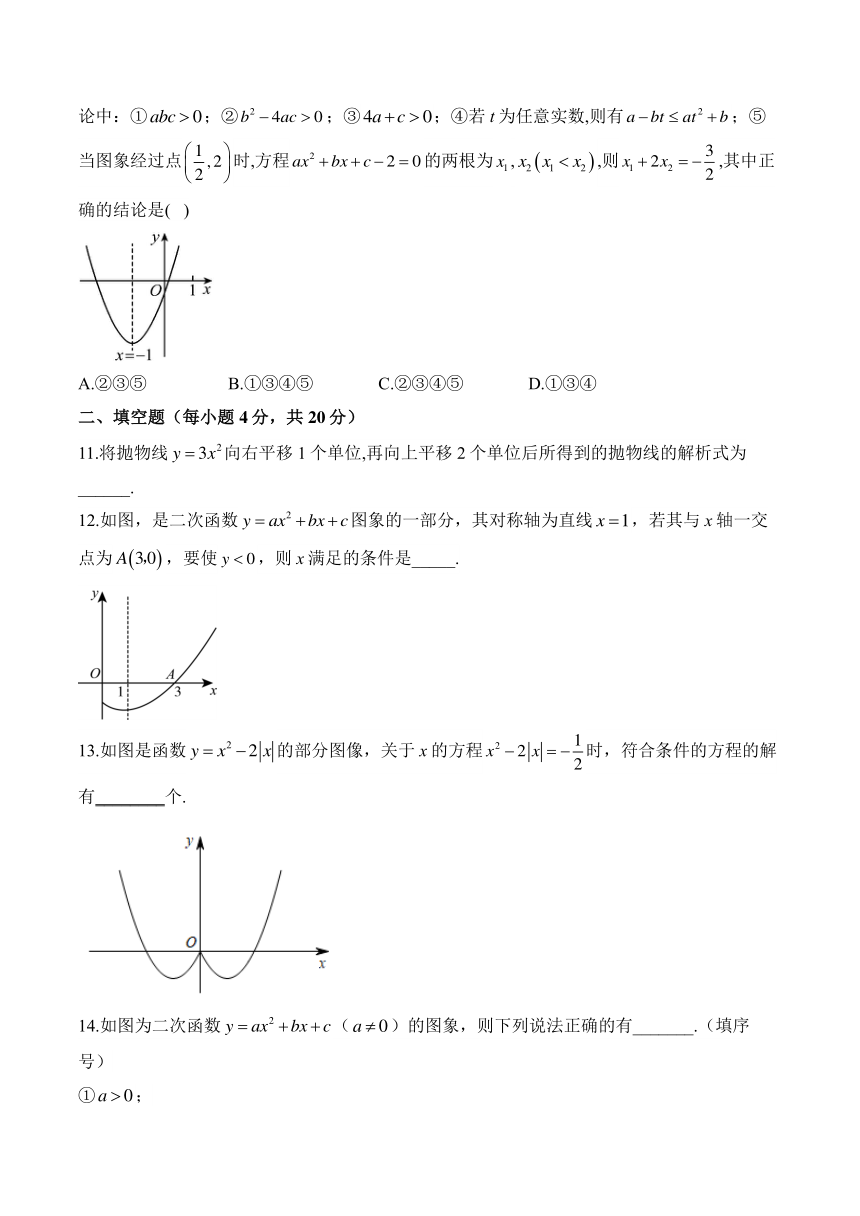
10.已知二次函数图象的对称轴为直线,部分图象如图所示,下列结论中:①;②;③;④若t为任意实数,则有;⑤当图象经过点时,方程的两根为,,则,其中正确的结论是( )
A.②③⑤ B.①③④⑤ C.②③④⑤ D.①③④
二、填空题(每小题4分,共20分)
11.将抛物线向右平移1个单位,再向上平移2个单位后所得到的抛物线的解析式为______.
12.如图,是二次函数图象的一部分,其对称轴为直线,若其与x轴一交点为,要使,则x满足的条件是_____.
13.如图是函数的部分图像,关于x的方程时,符合条件的方程的解有________个.
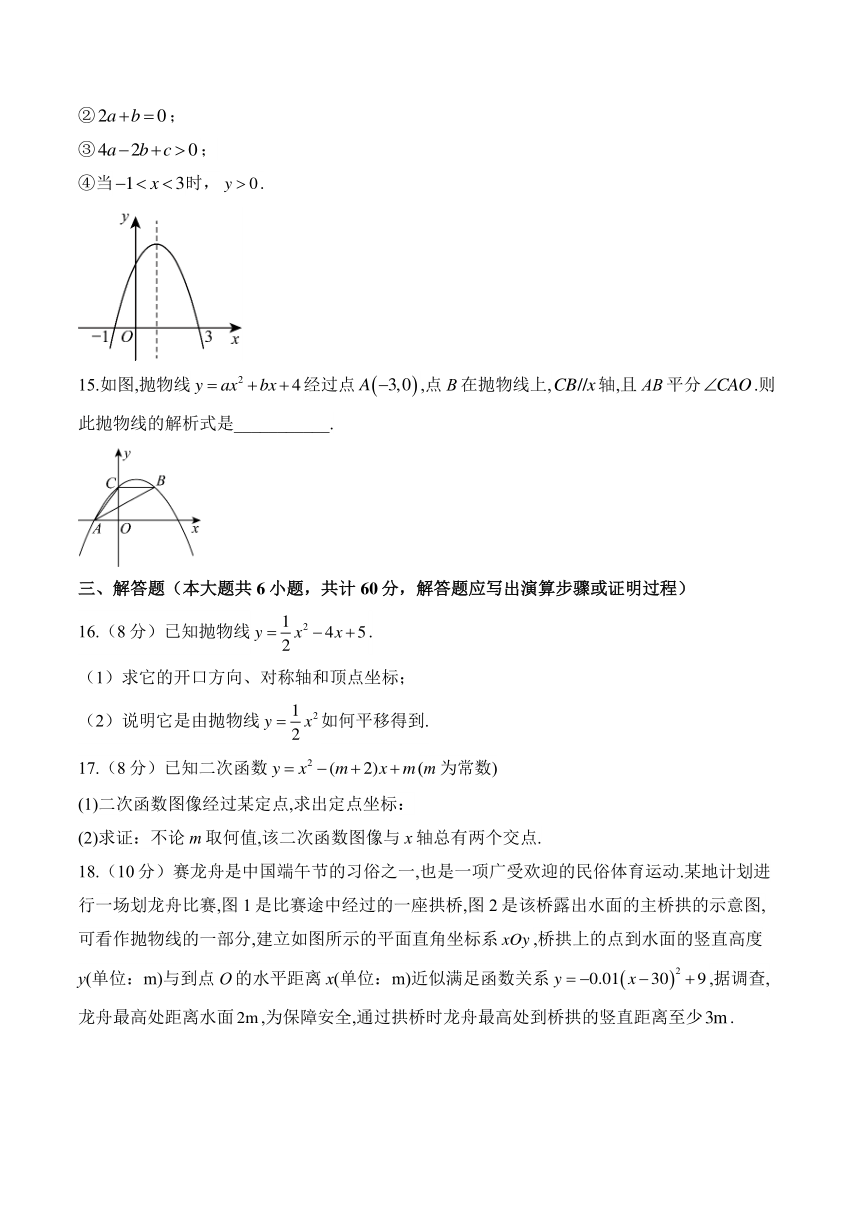
14.如图为二次函数()的图象,则下列说法正确的有_______.(填序号)
①;
②;
③;
④当时,.
15.如图,抛物线经过点,点B在抛物线上,轴,且AB平分.则此抛物线的解析式是___________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)已知抛物线.
(1)求它的开口方向、对称轴和顶点坐标;
(2)说明它是由抛物线如何平移得到.
17.(8分)已知二次函数(m为常数)
(1)二次函数图像经过某定点,求出定点坐标:
(2)求证:不论m取何值,该二次函数图像与x轴总有两个交点.
18.(10分)赛龙舟是中国端午节的习俗之一,也是一项广受欢迎的民俗体育运动.某地计划进行一场划龙舟比赛,图1是比赛途中经过的一座拱桥,图2是该桥露出水面的主桥拱的示意图,可看作抛物线的一部分,建立如图所示的平面直角坐标系,桥拱上的点到水面的竖直高度y(单位:m)与到点O的水平距离x(单位:m)近似满足函数关系,据调查,龙舟最高处距离水面,为保障安全,通过拱桥时龙舟最高处到桥拱的竖直距离至少.
(1)水面的宽度_______;
(2)要设计通过拱桥的龙舟赛道方案,若每条龙舟赛道宽度为,求最多可设计龙舟赛道的数量.
19.(10分)如图,,是一次函数与二次函数的图象的两个交点.
(1)求m,n的值和二次函数的解析式.
(2)请结合图象直接写出不等式的解集.
20.(12分)为满足市场需求,郴州某超市在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价提高1元,每天要少卖出20盒
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式:
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种月饼的每盒售价不得高于57元,如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售月饼多少盒?
21.(12分)如图.已知抛物线经过点和点,点C为抛物线与y轴的交点.
(1)求抛物线的解析式;
(2)若点E为直线上方抛物线上的一点,请求出面积的最大值.
答案以及解析
1.答案:D
解析:函数是二次函数,
,,
,,,
故选D.
2.答案:A
解析:A、B是抛物线上关于对称轴对称的两点,
抛物线对称轴为,
点A的横坐标是,点B横坐标为:2,
故选:A.
3.答案:B
解析:∵
∴顶点坐标为.
故选:B.
4.答案:D
解析:由题意得:,
故选:D.
5.答案:B
解析:因为抛物线的顶点坐标为,所以坐标原点在抛物线顶点的左侧,
又因为该抛物线的顶点在平面直角坐标系的横轴上,所以坐标原点可能是点Q.
6.答案:C
解析:抛物线的对称轴为直线,将抛物线向右平移2个单位长度得到抛物线,
抛物线的对称轴为直线,,
,
由图知抛物线的顶点在x轴上方,
抛物线的顶点在x轴上方,
,
.
故选:C.
7.答案:D
解析:对于,
A、当,即时,抛物线的开口向下,所以A选项不符合题意;
B、当,即,则时,y随x的增大而增大,所以B选项不符合题意;
C、抛物线的顶点坐标为,当时,抛物线开口向上,此时抛物线与x轴没有公共点,,所以C选项不符合题意;
D、当时,,则抛物线与y轴的交点坐标为,所以D选项符合题意.
故选:D.
8.答案:C
解析:以水面所在的直线为x轴,以这座抛物线型拱桥的对称轴为y轴,建立直角坐标系,
设抛物线的函数关系式为:,
∵抛物线过点,∴
又∵当桥下水面宽度是时,拱顶到水面的距离是,
∴抛物线经过点,∴,
解得
当水面下降后,
解得:,
∴水面的宽度是米,
故选:C.
9.答案:D
解析:二次函数的顶点坐标为,
二次函数图象的对称轴是直线,故选项A错误;
二次函数的图象与x轴的一个交点的横坐标是,对称轴是直线,
二次函数图象与x轴的另一个交点的横坐标是1,故选项B错误;
抛物线开口向下,对称轴是直线,
当时,y随x的增大而增大,故选项C错误;
设二次函数解析式为,
把代入,得,
解得,,
当时,,
二次函数图象与y轴的交点的纵坐标是3,故选项D正确,
故选D.
10.答案:C
解析:抛物线的开口向上,,
抛物线的对称轴为:,,
抛物线与y轴的交点在x轴的下方,,
,故①错误;
抛物线与x轴有两个交点,,故②正确;
时,,,且,
,
又,,故③正确;
时,y有最小值,
(t为任意实数),即,故④正确;
图象经过点时,方程的两根为,,
二次函数与直线的一个交点为:,
抛物线的对称轴为:,
二次函数与直线的另一个交点为:,
即,,
,故⑤正确,
正确的结论是②③④⑤,
故选C.
11.答案:
解析:将抛物线向右平移1个单位,再向上平移2个单位后,得到的新的抛物线的解析式为:.
故答案为:.
12.答案:
解析:∵二次函数的对称轴为直线,其与x轴一交点为,
∴二次函数与x轴的另一个交点为,
∴由函数图象可知,当时,,
∴要使,则x满足的条件是,
故答案为:.
13.答案:4
解析:如图,
当时,,顶点为,
当时,,顶点为,
关于x的方程时,
即和的交点的横坐标,
观察函数图象可知,交点有4个,即符合条件的方程的解有4个.
故答案为:4.
14.答案:②④
解析:①图象开口向下,可知,故①错误;
②对称轴在y轴右侧,,则有,即,故②正确;
③当时,,则,
根据,可得:,
,
,
故③错误;
④由图可知,当,,故④正确.
综上可知正确的有②④,
故答案为:②④.
15.答案:
解析:∵抛物线与y轴交于点C,
∴,∴,
∵,∴,
∴,
∵AB平分,
∴,
∵轴,
∴,
∴,
∴,
∴.
把、代入,
得,解得,
∴抛物线解析式为.
故答案为.
16.答案:(1)开口向上,对称轴为直线,顶点坐标为
(2)向右平移4个单位,向下平移3个单位得到的.
解析:(1),
抛物线开口向上,对称轴直线,顶点坐标为;
(2),
是由抛物线向右平移4个单位,向下平移3个单位得到的.
17.答案:(1)
(2)见解析
解析:(1)
令,即,解得
即二次函数过定点
(2)将代入可得
判别式,
一元二次方程有两个不相等的实数根
则不论m取何值,该二次函数图像与x轴总有两个交点.
18.答案:(1)60
(2)4条
解析:(1)令,则,
∴,
解得或,
∴,
∴,
故答案为:60;
(2)令,得,
∴
解得,.
可设计赛道的宽度为,
∵每条龙舟赛道宽度为,
最多可设计赛道4条.
19.答案:(1);;二次函数的解析式
(2)或
解析:(1)把的坐标代入,
得,
,
一次函数解析式为.
当时,,即,
.
把,的坐标分别代入,
得解得
.
(2)结合图象可知,不等式的解集为或.
20.答案:(1)
(2)每盒售价定为60元时,每天销售的利润P(元)最大,最大利润是8000元
(3)460盒
解析:(1)由题意得:;
(2),
,,
当时,元,
即当每盒售价定为60元时,每天销售的利润P(元)最大,最大利润是8000元;
(3)由题意,得,
解得,,
抛物线的开口向下,
当时,每天销售糕点的利润不低于6000元的利润,
又,.
在中,,
随x的增大而减小,
当时,,
即超市每天至少销售糕点460盒.
21.答案:(1)
(2)面积的最大值为
解析:(1)抛物线经过点和点,
将点和点代入抛物线解析式得:,
解得:,
抛物线解析式为;
(2)在抛物线中,令,则,
,
设直线的解析式为:,
将和代入直线的解析式得:,
解得:,
直线的解析式为,
如图,过点E作轴,交于点D,
,
设,则,
,
,
当时,最大,为,面积的最大值为.
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.当函数是二次函数时,a的取值为( )
A. B. C. D.
2.已知A、B是抛物线上关于对称轴对称的两点,若点A的横坐标是,则点B横坐标为( )
A.2 B.3 C.4 D.5
3.二次函数的顶点坐标是( )
A. B. C. D.
4.慈城某店家销售特产印花糕,经调查发现每盒印花糕售价为元时,日销售量为盒,当每盒售价每下降1元时,日销售量会增加5盒.已知每盒印花糕的成本为5元,设每盒降价x元,商家每天的利润为y元,则y与x之间的函数表达式为( )
A. B.
C. D.
5.若二次函数的图象如图所示,则坐标原点可能是( )
A.点P B.点Q C.点M D.点N
6.已知在平面直角坐标系中,抛物线的图象如图所示,对称轴为直线,将抛物线向右平移2个单位长度得到抛物线:(a、b、c为常数,且),则代数式与0的大小关系是( )
A. B. C. D.不能确定
7.已知二次函数,则下列表述正确的是( )
A.若,抛物线的开口向下 B.当时,y随x的增大而增大
C.图象与x轴一定有两个交点 D.图象与y轴的交点坐标为
8.如图所示,是一座抛物线型的拱桥,当桥下水面宽度是时,拱顶到水面的距离是,当水面下降后,水面的宽度是( )m.
A.6 B. C. D.
9.如图,二次函数的部分图象与x轴的一个交点的横坐标是,顶点坐标为,则下列说法正确的是( )
A.二次函数图象的对称轴是直线
B.二次函数图象与x轴的另一个交点的横坐标是2
C.当时,y随x的增大而减小
D.二次函数图象与y轴的交点的纵坐标是3
10.已知二次函数图象的对称轴为直线,部分图象如图所示,下列结论中:①;②;③;④若t为任意实数,则有;⑤当图象经过点时,方程的两根为,,则,其中正确的结论是( )
A.②③⑤ B.①③④⑤ C.②③④⑤ D.①③④
二、填空题(每小题4分,共20分)
11.将抛物线向右平移1个单位,再向上平移2个单位后所得到的抛物线的解析式为______.
12.如图,是二次函数图象的一部分,其对称轴为直线,若其与x轴一交点为,要使,则x满足的条件是_____.
13.如图是函数的部分图像,关于x的方程时,符合条件的方程的解有________个.
14.如图为二次函数()的图象,则下列说法正确的有_______.(填序号)
①;
②;
③;
④当时,.
15.如图,抛物线经过点,点B在抛物线上,轴,且AB平分.则此抛物线的解析式是___________.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)已知抛物线.
(1)求它的开口方向、对称轴和顶点坐标;
(2)说明它是由抛物线如何平移得到.
17.(8分)已知二次函数(m为常数)
(1)二次函数图像经过某定点,求出定点坐标:
(2)求证:不论m取何值,该二次函数图像与x轴总有两个交点.
18.(10分)赛龙舟是中国端午节的习俗之一,也是一项广受欢迎的民俗体育运动.某地计划进行一场划龙舟比赛,图1是比赛途中经过的一座拱桥,图2是该桥露出水面的主桥拱的示意图,可看作抛物线的一部分,建立如图所示的平面直角坐标系,桥拱上的点到水面的竖直高度y(单位:m)与到点O的水平距离x(单位:m)近似满足函数关系,据调查,龙舟最高处距离水面,为保障安全,通过拱桥时龙舟最高处到桥拱的竖直距离至少.
(1)水面的宽度_______;
(2)要设计通过拱桥的龙舟赛道方案,若每条龙舟赛道宽度为,求最多可设计龙舟赛道的数量.
19.(10分)如图,,是一次函数与二次函数的图象的两个交点.
(1)求m,n的值和二次函数的解析式.
(2)请结合图象直接写出不等式的解集.
20.(12分)为满足市场需求,郴州某超市在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价提高1元,每天要少卖出20盒
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式:
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种月饼的每盒售价不得高于57元,如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售月饼多少盒?
21.(12分)如图.已知抛物线经过点和点,点C为抛物线与y轴的交点.
(1)求抛物线的解析式;
(2)若点E为直线上方抛物线上的一点,请求出面积的最大值.
答案以及解析
1.答案:D
解析:函数是二次函数,
,,
,,,
故选D.
2.答案:A
解析:A、B是抛物线上关于对称轴对称的两点,
抛物线对称轴为,
点A的横坐标是,点B横坐标为:2,
故选:A.
3.答案:B
解析:∵
∴顶点坐标为.
故选:B.
4.答案:D
解析:由题意得:,
故选:D.
5.答案:B
解析:因为抛物线的顶点坐标为,所以坐标原点在抛物线顶点的左侧,
又因为该抛物线的顶点在平面直角坐标系的横轴上,所以坐标原点可能是点Q.
6.答案:C
解析:抛物线的对称轴为直线,将抛物线向右平移2个单位长度得到抛物线,
抛物线的对称轴为直线,,
,
由图知抛物线的顶点在x轴上方,
抛物线的顶点在x轴上方,
,
.
故选:C.
7.答案:D
解析:对于,
A、当,即时,抛物线的开口向下,所以A选项不符合题意;
B、当,即,则时,y随x的增大而增大,所以B选项不符合题意;
C、抛物线的顶点坐标为,当时,抛物线开口向上,此时抛物线与x轴没有公共点,,所以C选项不符合题意;
D、当时,,则抛物线与y轴的交点坐标为,所以D选项符合题意.
故选:D.
8.答案:C
解析:以水面所在的直线为x轴,以这座抛物线型拱桥的对称轴为y轴,建立直角坐标系,
设抛物线的函数关系式为:,
∵抛物线过点,∴
又∵当桥下水面宽度是时,拱顶到水面的距离是,
∴抛物线经过点,∴,
解得
当水面下降后,
解得:,
∴水面的宽度是米,
故选:C.
9.答案:D
解析:二次函数的顶点坐标为,
二次函数图象的对称轴是直线,故选项A错误;
二次函数的图象与x轴的一个交点的横坐标是,对称轴是直线,
二次函数图象与x轴的另一个交点的横坐标是1,故选项B错误;
抛物线开口向下,对称轴是直线,
当时,y随x的增大而增大,故选项C错误;
设二次函数解析式为,
把代入,得,
解得,,
当时,,
二次函数图象与y轴的交点的纵坐标是3,故选项D正确,
故选D.
10.答案:C
解析:抛物线的开口向上,,
抛物线的对称轴为:,,
抛物线与y轴的交点在x轴的下方,,
,故①错误;
抛物线与x轴有两个交点,,故②正确;
时,,,且,
,
又,,故③正确;
时,y有最小值,
(t为任意实数),即,故④正确;
图象经过点时,方程的两根为,,
二次函数与直线的一个交点为:,
抛物线的对称轴为:,
二次函数与直线的另一个交点为:,
即,,
,故⑤正确,
正确的结论是②③④⑤,
故选C.
11.答案:
解析:将抛物线向右平移1个单位,再向上平移2个单位后,得到的新的抛物线的解析式为:.
故答案为:.
12.答案:
解析:∵二次函数的对称轴为直线,其与x轴一交点为,
∴二次函数与x轴的另一个交点为,
∴由函数图象可知,当时,,
∴要使,则x满足的条件是,
故答案为:.
13.答案:4
解析:如图,
当时,,顶点为,
当时,,顶点为,
关于x的方程时,
即和的交点的横坐标,
观察函数图象可知,交点有4个,即符合条件的方程的解有4个.
故答案为:4.
14.答案:②④
解析:①图象开口向下,可知,故①错误;
②对称轴在y轴右侧,,则有,即,故②正确;
③当时,,则,
根据,可得:,
,
,
故③错误;
④由图可知,当,,故④正确.
综上可知正确的有②④,
故答案为:②④.
15.答案:
解析:∵抛物线与y轴交于点C,
∴,∴,
∵,∴,
∴,
∵AB平分,
∴,
∵轴,
∴,
∴,
∴,
∴.
把、代入,
得,解得,
∴抛物线解析式为.
故答案为.
16.答案:(1)开口向上,对称轴为直线,顶点坐标为
(2)向右平移4个单位,向下平移3个单位得到的.
解析:(1),
抛物线开口向上,对称轴直线,顶点坐标为;
(2),
是由抛物线向右平移4个单位,向下平移3个单位得到的.
17.答案:(1)
(2)见解析
解析:(1)
令,即,解得
即二次函数过定点
(2)将代入可得
判别式,
一元二次方程有两个不相等的实数根
则不论m取何值,该二次函数图像与x轴总有两个交点.
18.答案:(1)60
(2)4条
解析:(1)令,则,
∴,
解得或,
∴,
∴,
故答案为:60;
(2)令,得,
∴
解得,.
可设计赛道的宽度为,
∵每条龙舟赛道宽度为,
最多可设计赛道4条.
19.答案:(1);;二次函数的解析式
(2)或
解析:(1)把的坐标代入,
得,
,
一次函数解析式为.
当时,,即,
.
把,的坐标分别代入,
得解得
.
(2)结合图象可知,不等式的解集为或.
20.答案:(1)
(2)每盒售价定为60元时,每天销售的利润P(元)最大,最大利润是8000元
(3)460盒
解析:(1)由题意得:;
(2),
,,
当时,元,
即当每盒售价定为60元时,每天销售的利润P(元)最大,最大利润是8000元;
(3)由题意,得,
解得,,
抛物线的开口向下,
当时,每天销售糕点的利润不低于6000元的利润,
又,.
在中,,
随x的增大而减小,
当时,,
即超市每天至少销售糕点460盒.
21.答案:(1)
(2)面积的最大值为
解析:(1)抛物线经过点和点,
将点和点代入抛物线解析式得:,
解得:,
抛物线解析式为;
(2)在抛物线中,令,则,
,
设直线的解析式为:,
将和代入直线的解析式得:,
解得:,
直线的解析式为,
如图,过点E作轴,交于点D,
,
设,则,
,
,
当时,最大,为,面积的最大值为.
同课章节目录
