第二十四章 圆 九年级上册数学人教版(2012)单元练习(含答案)
文档属性
| 名称 | 第二十四章 圆 九年级上册数学人教版(2012)单元练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-03 00:00:00 | ||
图片预览


文档简介
圆
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.已知点P在半径为r的内,且,则r的值可能为( )
A.1 B.2 C.3 D.4
2.如图,,为的两条弦,连接,,若,则的度数为( )
A. B. C. D.
3.把半径为6,圆心角为的扇形围成一个圆锥的侧面,则这个圆锥的高为( )
A. B. C.2 D.
4.如图,在平面直角坐标系中,点,点,点.则经画图操作可知:的外接圆的圆心坐标是( )
A. B. C. D.
5.如图,AB、AC、BD是的切线,切点分别是P、C、D.若,,则BD的长是( )
A.4 B.3 C.2 D.1
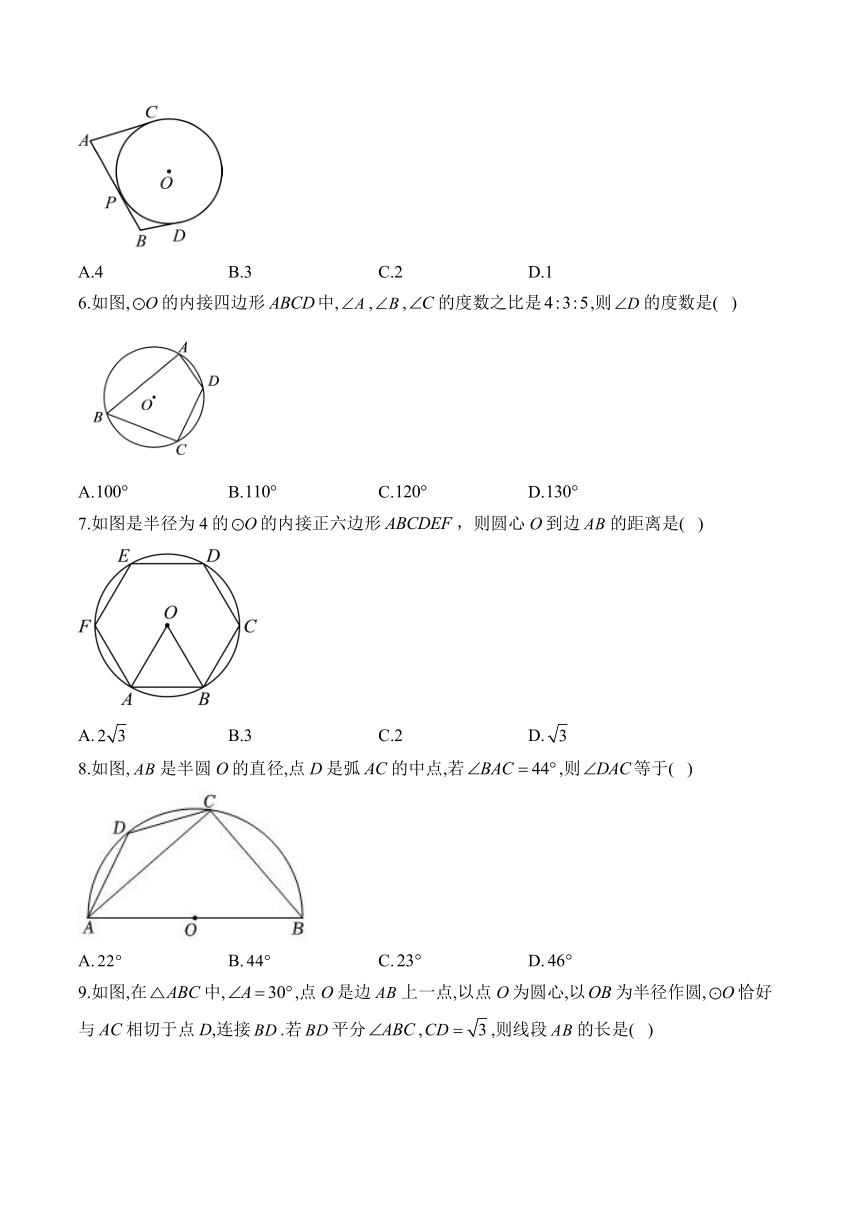
6.如图,的内接四边形中,,,的度数之比是,则的度数是( )
A. B. C. D.
7.如图是半径为4的的内接正六边形,则圆心O到边的距离是( )
A. B.3 C.2 D.
8.如图,是半圆O的直径,点D是弧的中点,若,则等于( )
A. B. C. D.
9.如图,在中,,点O是边上一点,以点O为圆心,以为半径作圆,恰好与相切于点D,连接.若平分,,则线段的长是( )
A. B. C.3 D.6
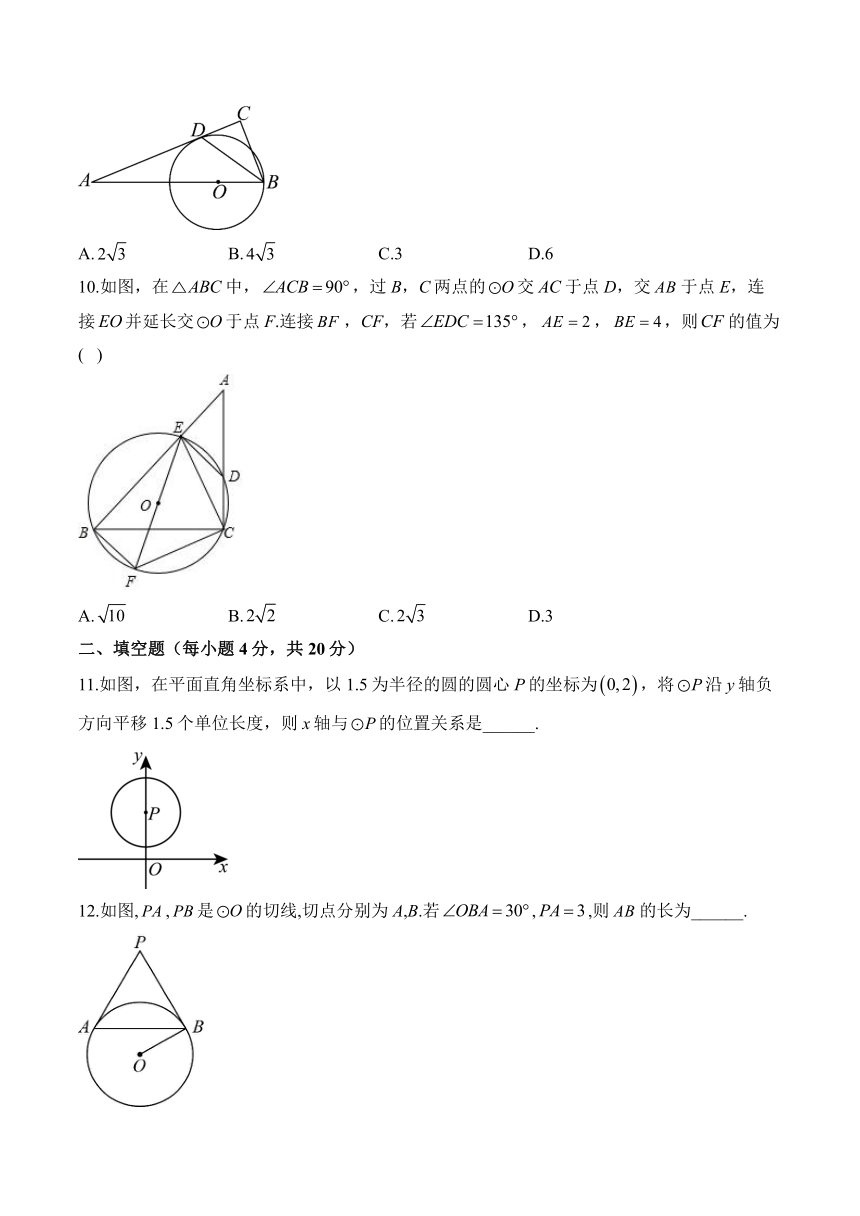
10.如图,在中,,过B,C两点的交于点D,交于点E,连接并延长交于点F.连接,CF,若,,,则的值为( )
A. B. C. D.3
二、填空题(每小题4分,共20分)
11.如图,在平面直角坐标系中,以1.5为半径的圆的圆心P的坐标为,将沿y轴负方向平移1.5个单位长度,则x轴与的位置关系是______.
12.如图,,是的切线,切点分别为A,B.若,,则的长为______.
13.如图,是半径为3的的切线,切点为A,的延长线交于点C,连接,若,则的长为___________________.
14.如图,在中,,,,则的内切圆半径______.
15.如图,扇形的半径,,则以为直径的半圆与围成的区域(图中阴影部分)的面积是______.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在中,是直径,是弦,延长,相交于点P,且,,求的度数.
17.(8分)如图,在中,,O为上一点.以O为圆心,长为半径的过点C,交于另一点D,若D是的中点,求证:是的切线.
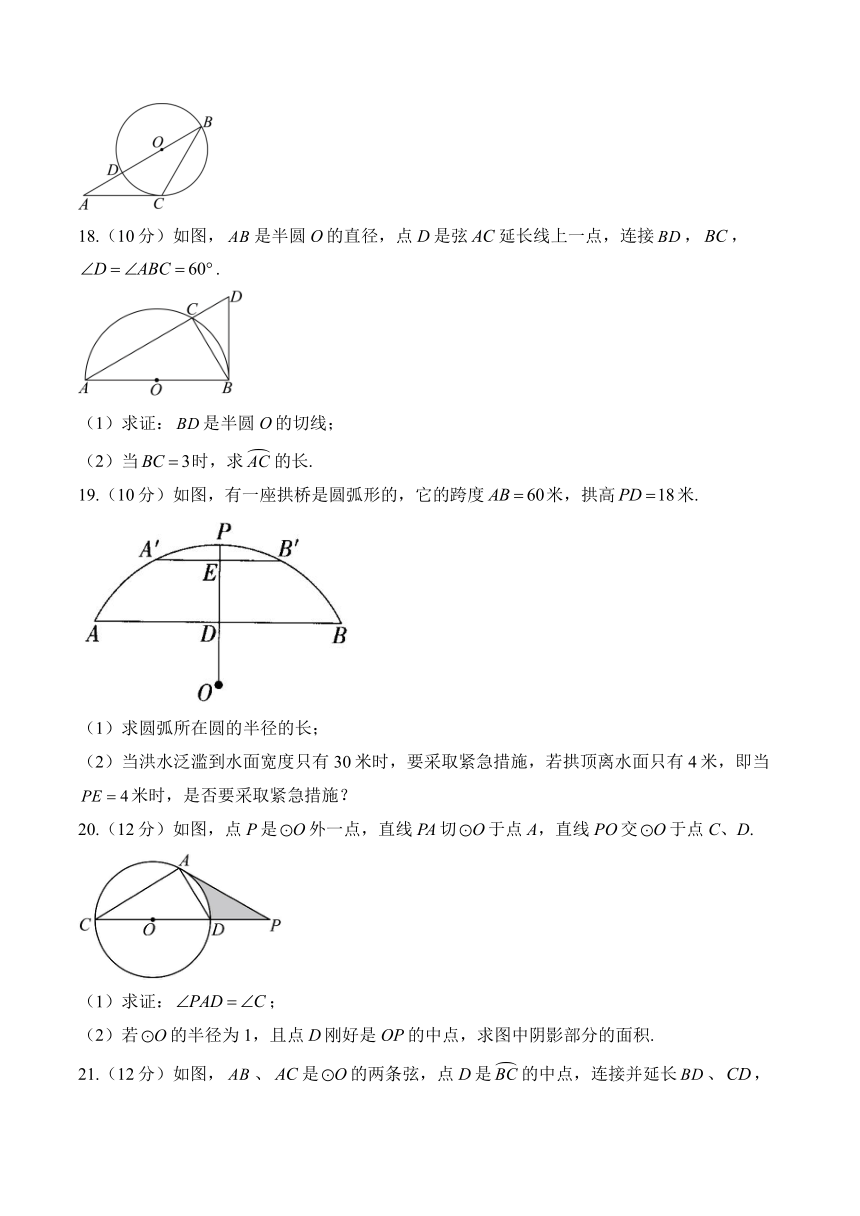
18.(10分)如图,是半圆O的直径,点D是弦延长线上一点,连接,,.
(1)求证:是半圆O的切线;
(2)当时,求的长.
19.(10分)如图,有一座拱桥是圆弧形的,它的跨度米,拱高米.
(1)求圆弧所在圆的半径的长;
(2)当洪水泛滥到水面宽度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即当米时,是否要采取紧急措施?
20.(12分)如图,点P是外一点,直线PA切于点A,直线PO交于点C、D.
(1)求证:;
(2)若的半径为1,且点D刚好是OP的中点,求图中阴影部分的面积.
21.(12分)如图,、是的两条弦,点D是的中点,连接并延长、,分别交、的延长线于点E、F.且.
(1)求证:;
(2)若,,求的半径.
答案以及解析
1.答案:D
解析:点P在半径为r的内,且,
.
故选:D.
2.答案:C
解析:根据题意,圆周角和圆心角同对着,
,
,
.
故选:C.
3.答案:A
解析:设此圆锥的底面半径为,
由题意,得,解得.
故圆锥的高为:.
故选:A.
4.答案:A
解析:的外心即是三角形三边垂直平分线的交点,
如图所示:EF与MN的交点即为所求的的外心,
的外心坐标是.
故选:A.
5.答案:C
解析:、为的切线,,
、为的切线,,
.
故选:C.
6.答案:C
解析:设为,则为,为,
∵四边形为圆内接四边形,
∴,,
∴,
解得:,
∴,
∴,
故选:C.
7.答案:A
解析:如图,做于点M,
正六边形外接半径为4的,
,,
,
,
,
圆心O到边的距离为,
故选:A.
8.答案:C
解析:是半圆O的直径,,
,,
四边形是半的内接四边形,
,
点D是弧的中点,
,
,
,
故选:C.
9.答案:D
解析:连接,
∵是的半径,是的切线,点D是切点,
∴,
∵,∴,
∵平分,∴,
∴,∴,
∴,∴,
∵,∴,
设,则,
∴由勾股定理得:,,
∴,
∴,
∴.
故选:D.
10.答案:A
解析:四边形内接于,且,
,
,
是等腰三角形,
,
又是的直径,
,
,
四边形是的内接四边形,
,
,
,
中,,
中,,
,
,
,
,
故选:A.
11.答案:相交
解析:,
,
将沿y轴负方向平移1.5个单位长度后,,
,
平移后x轴与的位置关系是相交,
故答案为:相交.
12.答案:3
解析:∵,是的切线,
∴,,
∵,
∴,
∴为等边三角形,
∴,
故答案为:3.
13.答案:
解析:连接,
∵是半径为3的的切线,
∴,
又,
∴,
∴的长为,
故答案为:.
14.答案:1
解析:设的内切圆与、、分别相切于点D、E、F,
,,
,
四边形是矩形,
,
四边形是正方形,
,
,,
,,
,,
在中,,
,
,
解得.
故答案为:1.
15.答案:
解析:过点O作于点P,
∴,
∵,,
∴,
∴,
∴,
在中,由勾股定理得:,
∴,
∴,
∴,
∵扇形的半径,,
∴,
∴,
,
∴阴影部分的面积是,
故答案为:.
16.答案:
解析:连接,
,,
,
.
是的外角,
.
,
,
,
.
17.答案:见解析
解析:证明:连接,.
,
.
是直径,
.
D是的中点,
.
又,
.
,
,
.
点C为半径的外端点,
是的切线.
18.答案:(1)见解析
(2)
解析:(1)证明:是半圆O的直径,
,
,
,
,
是半圆O的切线;
(2)如图,连接,
,,
为等边三角形,
,,
,
.
19、(1)答案:34米
解析:如图,连接OA.设圆弧所在圆的半径为r米.由题意可知拱高米,,米,米.在中,由勾股定理得,即,解得.
圆弧所在圆的半径的长为34米.
(2)答案:不需要采取紧急措施,理由见解析
解析:如图,连接.由(1)知米,
(米),
在中,由勾股定理得(米).
易知,米.,
当拱顶离水面只有4米时,不需要采取紧急措施.
20.答案:(1)见解析
(2)
解析:(1)证明:连接OA,
是的切线,
,
,
是的直径,
,
,
,
,
;
(2),,D是OP的中点,
,,
为等边三角形,
,
,
.
21.答案:(1)见解析
(2)
解析:(1)证明:点D是的中点,
,,
,,
,
,,
,
,
,
,
;
(2)连接,
,
,
点D是的中点,
,
,
,
,
是的直径,
,
又,
在中,,
令,在中,由,
得,
解得,即,
在中,,
的半径为.
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.已知点P在半径为r的内,且,则r的值可能为( )
A.1 B.2 C.3 D.4
2.如图,,为的两条弦,连接,,若,则的度数为( )
A. B. C. D.
3.把半径为6,圆心角为的扇形围成一个圆锥的侧面,则这个圆锥的高为( )
A. B. C.2 D.
4.如图,在平面直角坐标系中,点,点,点.则经画图操作可知:的外接圆的圆心坐标是( )
A. B. C. D.
5.如图,AB、AC、BD是的切线,切点分别是P、C、D.若,,则BD的长是( )
A.4 B.3 C.2 D.1
6.如图,的内接四边形中,,,的度数之比是,则的度数是( )
A. B. C. D.
7.如图是半径为4的的内接正六边形,则圆心O到边的距离是( )
A. B.3 C.2 D.
8.如图,是半圆O的直径,点D是弧的中点,若,则等于( )
A. B. C. D.
9.如图,在中,,点O是边上一点,以点O为圆心,以为半径作圆,恰好与相切于点D,连接.若平分,,则线段的长是( )
A. B. C.3 D.6
10.如图,在中,,过B,C两点的交于点D,交于点E,连接并延长交于点F.连接,CF,若,,,则的值为( )
A. B. C. D.3
二、填空题(每小题4分,共20分)
11.如图,在平面直角坐标系中,以1.5为半径的圆的圆心P的坐标为,将沿y轴负方向平移1.5个单位长度,则x轴与的位置关系是______.
12.如图,,是的切线,切点分别为A,B.若,,则的长为______.
13.如图,是半径为3的的切线,切点为A,的延长线交于点C,连接,若,则的长为___________________.
14.如图,在中,,,,则的内切圆半径______.
15.如图,扇形的半径,,则以为直径的半圆与围成的区域(图中阴影部分)的面积是______.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)如图,在中,是直径,是弦,延长,相交于点P,且,,求的度数.
17.(8分)如图,在中,,O为上一点.以O为圆心,长为半径的过点C,交于另一点D,若D是的中点,求证:是的切线.
18.(10分)如图,是半圆O的直径,点D是弦延长线上一点,连接,,.
(1)求证:是半圆O的切线;
(2)当时,求的长.
19.(10分)如图,有一座拱桥是圆弧形的,它的跨度米,拱高米.
(1)求圆弧所在圆的半径的长;
(2)当洪水泛滥到水面宽度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即当米时,是否要采取紧急措施?
20.(12分)如图,点P是外一点,直线PA切于点A,直线PO交于点C、D.
(1)求证:;
(2)若的半径为1,且点D刚好是OP的中点,求图中阴影部分的面积.
21.(12分)如图,、是的两条弦,点D是的中点,连接并延长、,分别交、的延长线于点E、F.且.
(1)求证:;
(2)若,,求的半径.
答案以及解析
1.答案:D
解析:点P在半径为r的内,且,
.
故选:D.
2.答案:C
解析:根据题意,圆周角和圆心角同对着,
,
,
.
故选:C.
3.答案:A
解析:设此圆锥的底面半径为,
由题意,得,解得.
故圆锥的高为:.
故选:A.
4.答案:A
解析:的外心即是三角形三边垂直平分线的交点,
如图所示:EF与MN的交点即为所求的的外心,
的外心坐标是.
故选:A.
5.答案:C
解析:、为的切线,,
、为的切线,,
.
故选:C.
6.答案:C
解析:设为,则为,为,
∵四边形为圆内接四边形,
∴,,
∴,
解得:,
∴,
∴,
故选:C.
7.答案:A
解析:如图,做于点M,
正六边形外接半径为4的,
,,
,
,
,
圆心O到边的距离为,
故选:A.
8.答案:C
解析:是半圆O的直径,,
,,
四边形是半的内接四边形,
,
点D是弧的中点,
,
,
,
故选:C.
9.答案:D
解析:连接,
∵是的半径,是的切线,点D是切点,
∴,
∵,∴,
∵平分,∴,
∴,∴,
∴,∴,
∵,∴,
设,则,
∴由勾股定理得:,,
∴,
∴,
∴.
故选:D.
10.答案:A
解析:四边形内接于,且,
,
,
是等腰三角形,
,
又是的直径,
,
,
四边形是的内接四边形,
,
,
,
中,,
中,,
,
,
,
,
故选:A.
11.答案:相交
解析:,
,
将沿y轴负方向平移1.5个单位长度后,,
,
平移后x轴与的位置关系是相交,
故答案为:相交.
12.答案:3
解析:∵,是的切线,
∴,,
∵,
∴,
∴为等边三角形,
∴,
故答案为:3.
13.答案:
解析:连接,
∵是半径为3的的切线,
∴,
又,
∴,
∴的长为,
故答案为:.
14.答案:1
解析:设的内切圆与、、分别相切于点D、E、F,
,,
,
四边形是矩形,
,
四边形是正方形,
,
,,
,,
,,
在中,,
,
,
解得.
故答案为:1.
15.答案:
解析:过点O作于点P,
∴,
∵,,
∴,
∴,
∴,
在中,由勾股定理得:,
∴,
∴,
∴,
∵扇形的半径,,
∴,
∴,
,
∴阴影部分的面积是,
故答案为:.
16.答案:
解析:连接,
,,
,
.
是的外角,
.
,
,
,
.
17.答案:见解析
解析:证明:连接,.
,
.
是直径,
.
D是的中点,
.
又,
.
,
,
.
点C为半径的外端点,
是的切线.
18.答案:(1)见解析
(2)
解析:(1)证明:是半圆O的直径,
,
,
,
,
是半圆O的切线;
(2)如图,连接,
,,
为等边三角形,
,,
,
.
19、(1)答案:34米
解析:如图,连接OA.设圆弧所在圆的半径为r米.由题意可知拱高米,,米,米.在中,由勾股定理得,即,解得.
圆弧所在圆的半径的长为34米.
(2)答案:不需要采取紧急措施,理由见解析
解析:如图,连接.由(1)知米,
(米),
在中,由勾股定理得(米).
易知,米.,
当拱顶离水面只有4米时,不需要采取紧急措施.
20.答案:(1)见解析
(2)
解析:(1)证明:连接OA,
是的切线,
,
,
是的直径,
,
,
,
,
;
(2),,D是OP的中点,
,,
为等边三角形,
,
,
.
21.答案:(1)见解析
(2)
解析:(1)证明:点D是的中点,
,,
,,
,
,,
,
,
,
,
;
(2)连接,
,
,
点D是的中点,
,
,
,
,
是的直径,
,
又,
在中,,
令,在中,由,
得,
解得,即,
在中,,
的半径为.
同课章节目录
