选择必修 第二章 2.3.2 两点间的距离公式 课件(共24张PPT)
文档属性
| 名称 | 选择必修 第二章 2.3.2 两点间的距离公式 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-09-18 10:34:49 | ||
图片预览








文档简介
(共24张PPT)
选择必修
第二章 直线和圆的方程
2.3 直线的交点坐标与距离公式
2.3.2 两点间的距离公式
教学目标
学习目标 数学素养
1.会用向量的方法推导两点间的距离公式. 1.数形结合素养和数学运算素养.
2.理解平面直角坐标系两点间的距离公式的结构特点,并会求两点间的距离及其简单的应用. 2.数学运算素养和逻辑推理素养.
3.会用坐标法解决平面几何中的问题. 3.数形结合素养.
温故知新
1.求两条相交直线的交点坐标
②解方程组;
①联立方程组;
③得交点坐标.
2.判断两条直线的位置关系
线的位置关系 公共点的个数 方程组解的个数
相交
平行
重合
有且仅有1个
唯一解
0个
无解
无数个
无数组解
新知探究
我们知道,在各种几何量中,直线段的长度是最基本的. 所以,在解析几何中,最基本的公式自然是用平面内两点的坐标表示这两点间距离的公式.
如下图, 已知平面内两点P1(x1,y1)、P2(x2,y2),
如何求P1、P2间的距离| P1P2|
在学习向量及其运算的坐标表示时,我们定义有向线段,利用向量的模求的长度(模).
新知探究
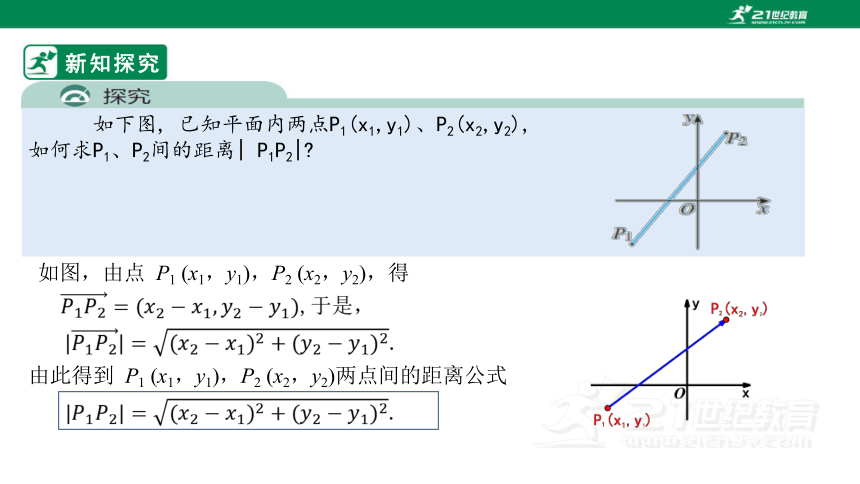
如下图, 已知平面内两点P1(x1,y1)、P2(x2,y2),
如何求P1、P2间的距离| P1P2|
如图,由点 P1 (x1,y1),P2 (x2,y2),得
,于是,
.
由此得到 P1 (x1,y1),P2 (x2,y2)两点间的距离公式
.
新知探究
特别的,原点O(0,0)与任一点P(x,y)间的距离
.
平面内两点 P1 (x1,y1),P2 (x2,y2),
.
新知探究
你能利用 P1 (x1,y1),P2 (x2,y2) 构造直角三角形,再用勾股定理推导两点间的距离公式吗?与向量法比较,你有什么体会?
分类讨论:
① x1 = x2, y1 ≠ y2:|P1P2| = | y2 – y1 |;
x
y
O
P2 (x2,y2)
P1 (x1,y1)
①
② x1 ≠ x2, y1 = y2:|P1P2| = | x2 – x1 |;
x
y
O
P1 (x1,y1)
P2 (x2,y2)
②
x
y
O
P1 (x1,y1)
P2 (x2,y2)
③
Q (x2,y1)
③ x1 ≠ x2,y1 ≠ y2:
|P1Q| = | x2 – x1 |,|P2Q| = | y2 – y1 |,
|P1P2| = .
新知探究
1. 两点间的距离公式:
平面内两点 P1 (x1,y1),P2 (x2,y2),
.
① 原点 O (0,0) 与任一点 P (x,y) 间的距离:.
② 当直线P1P2垂直于x轴时:|| = ||;
③ 当直线P1P2垂直于y轴时:|| = ||.
2. 两点间的距离公式与两点的先后顺序无关:
.
知新探究
【例1】求下列两点间的距离:
⑴P (-6,0),Q (0, 2); ⑵A(3,-1),B(-1,3);
⑶M(-2,-3),N(-2,4).
解:
⑴代入两点间距离公式得:|PQ|=.
⑶∵M与N的横坐标都是-2,
⑵代入两点间距离公式得:|AB|=.
∴|MN|=|4-(-3)|=7.
初试身手
1.已知点A(-3,1),B(3,-3),C(1,7),试判断此三角形的形状,并求其面积.
解:
∵|AB|=,
|AC|=,
|BC|=,
∴|AB|2+|AC|2=|BC|2,且|AB|=|AC|,
∴△ABC是等腰直角三角形.
∴S△ABC=.
知新探究
【例2】已知点 A ( 1,2),B (2,),在x轴上求一点P,使|PA|=|PB|,并求|PA|的值.
解:
方法1:设所求点为P (x,0),则
|PA|,
|PB|=,
由|PA|=|PB|,得
2 + 2 + 5 = 2 4 + 11,
解得 x=1,
∴所求点为P (1,0),且
|PA|.
知新探究
【例2】已知点 A ( 1,2),B (2,),在x轴上求一点P,使|PA|=|PB|,并求|PA|的值.
解:
方法2:由|PA|=|PB|,得点P在AB的垂直平分线上,
而AB的斜率为,
,
则AB的垂直平分线的斜率,
∴AB的垂直平分线的方程为
由点P在x轴上,令y=0,解得x=1,
∴所求点为P (1,0),且
|PA|.
初试身手
解:
⑴由题意可知,E为AB的中点,kAB==-1,
∴E(3,2),且kCE==1,
∴CE所在直线方程为y-2=x-3,
即x-y-1=0.
⑵由,解得,
2.已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
⑴求AB边上的高CE所在直线的方程;
⑵求△ABC的面积.
所以C(4,3).
初试身手
解:
又因为A(2,3),B(4,1),
∴|EC|=,
|AB|=,
∴S△ABC==2.
2.已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
⑴求AB边上的高CE所在直线的方程;
⑵求△ABC的面积.
新知探究
【例3】用坐标法证明:平行四边形四条边的平方和等于两条对角线的平方和.
分析:首先要建立适当的平面直角坐标系,用坐标表示有关的量,然后进行代数运算,最后把运算结果“翻译”成几何关系.
如右图,以顶点A为坐标原点,AB边所在的直线为x轴,建立直角坐标系,则有A(0,0).
由两点间的距离公式,得
证明:
y
x
O
A
B
D
C
(0,0)
(a,0)
(a+b,c)
(b,c)
设B(a,0),D(b,c),
由平行四边形的性质,得C(a+b,c).
如何由平行四边形的性质,得到点C的坐标为(a+b,c)?
|AC| =(a+b) +c ,
BD| =(b-a) +c ,
|AB| =a ,
|AD| =b +c ,|
∴|AC| +|BD| =2(a +b +c ),|AB| +|AD| =a +b +c ,|
∴|AC| +|BD| =2(|AB| +|AD| ).
即平行四边形四条边的平方和等于两条对角线的平方和.
初试身手
2.△ABD和△BCE是在直线AC同侧的两个等边三角形,已知A,B,C三点在同一直线上,用坐标法证明|AE|=|CD|.
证明:
如图,以B为坐标原点,直线AC为x轴,建立平面直角坐标系.
设△ABD和△BCE的边长分别为a,c,
则A(-a,0),C(c,0),D(),E(),
∴|AE|=,
|CD|=,
∴|AE|=|CD|.
新知探究
在“平面向量及其应用”的学习中,我们用“向量法”证明过这个命题.你能回忆一下证明过程吗 比较“坐标法”和“向量法”,你有什么体会
用向量表示问题中的 几何元素
把向量运算结果“翻 译”成几何结论
进行有关 向量运算
D C
A B
新知探究
建立坐标系,用坐标 表示有关的量
把代数运算结果“翻 译”成几何结论
进行有关 代数运算
用“坐标法”解决平面几何问题的基本步骤可以概括为:
(1)建立坐标系,尽可能将有关元素放在坐标轴上;
(2)用坐标表示有关的量;
(3)将几何关系转化为坐标运算;
(4)把代数运算结果“翻译"成几何关系.
新知探究
根据例3的条件,你是否还有其他建立坐标系的方法 你能说说建立适当坐标系对证明的重要性吗
用坐标法解决几何问题时,关键是要结合图形的特征,建立平面直角坐标系. 建立的坐标系是否合适,会直接影响问题能否方便解决. 建系的原则主要有两点:
⑴让尽可能多的点落在坐标轴上,这样便于运算;
⑵如果条件中有互相垂直的两条线, 要考虑将它们作为坐标轴;如果图形为中心对称图形,可考虑将中心作为原点;如果图形为轴对称图形,可考虑将对称轴作为坐标轴.
课堂小结
2.利用“坐标法”解决平面几何问题的基本步骤:
1. 两点间的距离公式:
平面内两点 P1 (x1,y1),P2 (x2,y2),
.
① 原点 O (0,0) 与任一点 P (x,y) 间的距离:.
② 当直线P1P2垂直于x轴时:|| = ||;
③ 当直线P1P2垂直于y轴时:|| = ||.
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算
第三步:把代数运算的结果“翻译”成几何结论
作业布置
作业:
P79-80 习题2.3 第4,5,11,12题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修
第二章 直线和圆的方程
2.3 直线的交点坐标与距离公式
2.3.2 两点间的距离公式
教学目标
学习目标 数学素养
1.会用向量的方法推导两点间的距离公式. 1.数形结合素养和数学运算素养.
2.理解平面直角坐标系两点间的距离公式的结构特点,并会求两点间的距离及其简单的应用. 2.数学运算素养和逻辑推理素养.
3.会用坐标法解决平面几何中的问题. 3.数形结合素养.
温故知新
1.求两条相交直线的交点坐标
②解方程组;
①联立方程组;
③得交点坐标.
2.判断两条直线的位置关系
线的位置关系 公共点的个数 方程组解的个数
相交
平行
重合
有且仅有1个
唯一解
0个
无解
无数个
无数组解
新知探究
我们知道,在各种几何量中,直线段的长度是最基本的. 所以,在解析几何中,最基本的公式自然是用平面内两点的坐标表示这两点间距离的公式.
如下图, 已知平面内两点P1(x1,y1)、P2(x2,y2),
如何求P1、P2间的距离| P1P2|
在学习向量及其运算的坐标表示时,我们定义有向线段,利用向量的模求的长度(模).
新知探究
如下图, 已知平面内两点P1(x1,y1)、P2(x2,y2),
如何求P1、P2间的距离| P1P2|
如图,由点 P1 (x1,y1),P2 (x2,y2),得
,于是,
.
由此得到 P1 (x1,y1),P2 (x2,y2)两点间的距离公式
.
新知探究
特别的,原点O(0,0)与任一点P(x,y)间的距离
.
平面内两点 P1 (x1,y1),P2 (x2,y2),
.
新知探究
你能利用 P1 (x1,y1),P2 (x2,y2) 构造直角三角形,再用勾股定理推导两点间的距离公式吗?与向量法比较,你有什么体会?
分类讨论:
① x1 = x2, y1 ≠ y2:|P1P2| = | y2 – y1 |;
x
y
O
P2 (x2,y2)
P1 (x1,y1)
①
② x1 ≠ x2, y1 = y2:|P1P2| = | x2 – x1 |;
x
y
O
P1 (x1,y1)
P2 (x2,y2)
②
x
y
O
P1 (x1,y1)
P2 (x2,y2)
③
Q (x2,y1)
③ x1 ≠ x2,y1 ≠ y2:
|P1Q| = | x2 – x1 |,|P2Q| = | y2 – y1 |,
|P1P2| = .
新知探究
1. 两点间的距离公式:
平面内两点 P1 (x1,y1),P2 (x2,y2),
.
① 原点 O (0,0) 与任一点 P (x,y) 间的距离:.
② 当直线P1P2垂直于x轴时:|| = ||;
③ 当直线P1P2垂直于y轴时:|| = ||.
2. 两点间的距离公式与两点的先后顺序无关:
.
知新探究
【例1】求下列两点间的距离:
⑴P (-6,0),Q (0, 2); ⑵A(3,-1),B(-1,3);
⑶M(-2,-3),N(-2,4).
解:
⑴代入两点间距离公式得:|PQ|=.
⑶∵M与N的横坐标都是-2,
⑵代入两点间距离公式得:|AB|=.
∴|MN|=|4-(-3)|=7.
初试身手
1.已知点A(-3,1),B(3,-3),C(1,7),试判断此三角形的形状,并求其面积.
解:
∵|AB|=,
|AC|=,
|BC|=,
∴|AB|2+|AC|2=|BC|2,且|AB|=|AC|,
∴△ABC是等腰直角三角形.
∴S△ABC=.
知新探究
【例2】已知点 A ( 1,2),B (2,),在x轴上求一点P,使|PA|=|PB|,并求|PA|的值.
解:
方法1:设所求点为P (x,0),则
|PA|,
|PB|=,
由|PA|=|PB|,得
2 + 2 + 5 = 2 4 + 11,
解得 x=1,
∴所求点为P (1,0),且
|PA|.
知新探究
【例2】已知点 A ( 1,2),B (2,),在x轴上求一点P,使|PA|=|PB|,并求|PA|的值.
解:
方法2:由|PA|=|PB|,得点P在AB的垂直平分线上,
而AB的斜率为,
,
则AB的垂直平分线的斜率,
∴AB的垂直平分线的方程为
由点P在x轴上,令y=0,解得x=1,
∴所求点为P (1,0),且
|PA|.
初试身手
解:
⑴由题意可知,E为AB的中点,kAB==-1,
∴E(3,2),且kCE==1,
∴CE所在直线方程为y-2=x-3,
即x-y-1=0.
⑵由,解得,
2.已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
⑴求AB边上的高CE所在直线的方程;
⑵求△ABC的面积.
所以C(4,3).
初试身手
解:
又因为A(2,3),B(4,1),
∴|EC|=,
|AB|=,
∴S△ABC==2.
2.已知点A(2,3),B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
⑴求AB边上的高CE所在直线的方程;
⑵求△ABC的面积.
新知探究
【例3】用坐标法证明:平行四边形四条边的平方和等于两条对角线的平方和.
分析:首先要建立适当的平面直角坐标系,用坐标表示有关的量,然后进行代数运算,最后把运算结果“翻译”成几何关系.
如右图,以顶点A为坐标原点,AB边所在的直线为x轴,建立直角坐标系,则有A(0,0).
由两点间的距离公式,得
证明:
y
x
O
A
B
D
C
(0,0)
(a,0)
(a+b,c)
(b,c)
设B(a,0),D(b,c),
由平行四边形的性质,得C(a+b,c).
如何由平行四边形的性质,得到点C的坐标为(a+b,c)?
|AC| =(a+b) +c ,
BD| =(b-a) +c ,
|AB| =a ,
|AD| =b +c ,|
∴|AC| +|BD| =2(a +b +c ),|AB| +|AD| =a +b +c ,|
∴|AC| +|BD| =2(|AB| +|AD| ).
即平行四边形四条边的平方和等于两条对角线的平方和.
初试身手
2.△ABD和△BCE是在直线AC同侧的两个等边三角形,已知A,B,C三点在同一直线上,用坐标法证明|AE|=|CD|.
证明:
如图,以B为坐标原点,直线AC为x轴,建立平面直角坐标系.
设△ABD和△BCE的边长分别为a,c,
则A(-a,0),C(c,0),D(),E(),
∴|AE|=,
|CD|=,
∴|AE|=|CD|.
新知探究
在“平面向量及其应用”的学习中,我们用“向量法”证明过这个命题.你能回忆一下证明过程吗 比较“坐标法”和“向量法”,你有什么体会
用向量表示问题中的 几何元素
把向量运算结果“翻 译”成几何结论
进行有关 向量运算
D C
A B
新知探究
建立坐标系,用坐标 表示有关的量
把代数运算结果“翻 译”成几何结论
进行有关 代数运算
用“坐标法”解决平面几何问题的基本步骤可以概括为:
(1)建立坐标系,尽可能将有关元素放在坐标轴上;
(2)用坐标表示有关的量;
(3)将几何关系转化为坐标运算;
(4)把代数运算结果“翻译"成几何关系.
新知探究
根据例3的条件,你是否还有其他建立坐标系的方法 你能说说建立适当坐标系对证明的重要性吗
用坐标法解决几何问题时,关键是要结合图形的特征,建立平面直角坐标系. 建立的坐标系是否合适,会直接影响问题能否方便解决. 建系的原则主要有两点:
⑴让尽可能多的点落在坐标轴上,这样便于运算;
⑵如果条件中有互相垂直的两条线, 要考虑将它们作为坐标轴;如果图形为中心对称图形,可考虑将中心作为原点;如果图形为轴对称图形,可考虑将对称轴作为坐标轴.
课堂小结
2.利用“坐标法”解决平面几何问题的基本步骤:
1. 两点间的距离公式:
平面内两点 P1 (x1,y1),P2 (x2,y2),
.
① 原点 O (0,0) 与任一点 P (x,y) 间的距离:.
② 当直线P1P2垂直于x轴时:|| = ||;
③ 当直线P1P2垂直于y轴时:|| = ||.
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算
第三步:把代数运算的结果“翻译”成几何结论
作业布置
作业:
P79-80 习题2.3 第4,5,11,12题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
