13.1三角形中的边角关系第3课时三角形中几条重要线段课件(共26张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 13.1三角形中的边角关系第3课时三角形中几条重要线段课件(共26张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 458.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
沪科版
13.1.3 三角形中几条重要线段
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.掌握三角形的高,中线及角平分线的概念及画法.
2.掌握三角形的高,中线及角平分线的简单应用.
3.通过具体实例,了解定义的意义.
学习目标
重点
难点
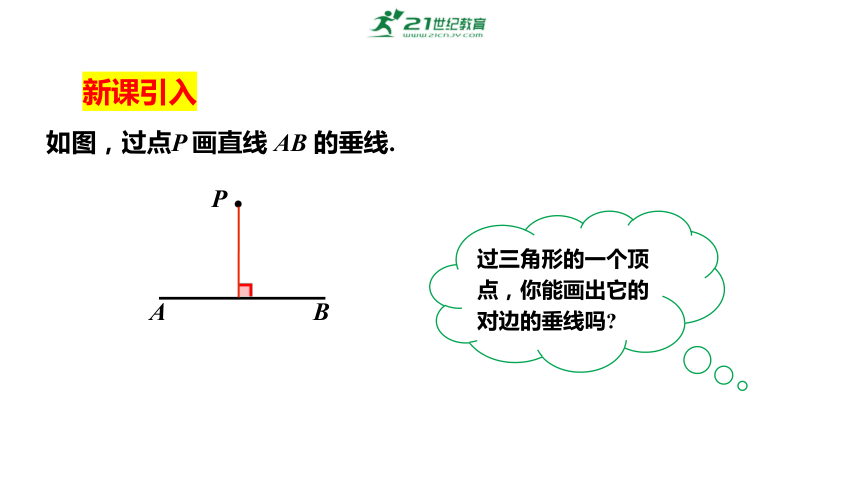
过三角形的一个顶点,你能画出它的对边的垂线吗
如图,过点P 画直线 AB 的垂线.
P ●
A
B
新课引入
一、三角形的高
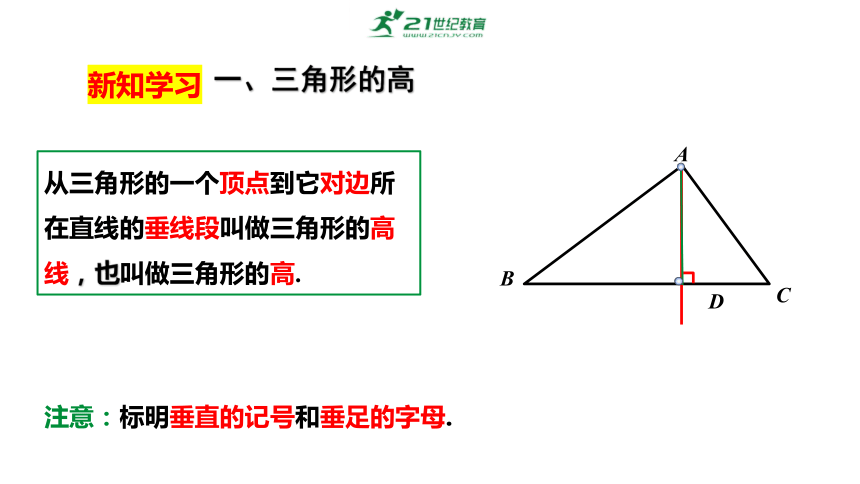
从三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线,也叫做三角形的高.
A
B
C
D
注意:标明垂直的记号和垂足的字母.
新知学习
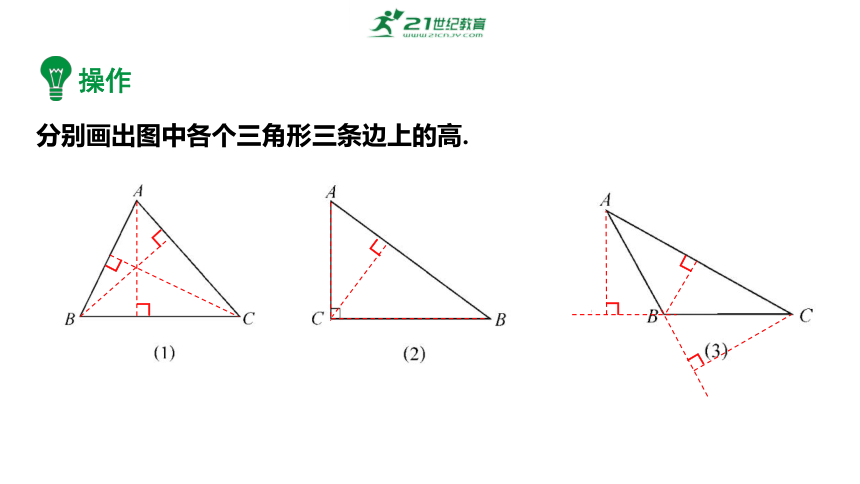
分别画出图中各个三角形三条边上的高.
操作
∟
∟
∟
∟
∟
∟
∟
思考:锐角三角形、直角三角形、钝角三角形中的三条高所在直线的交点各在什么地方
①锐角三角形三条高线都在三角形的内部且交于同一点(三角形的垂心);
②直角三角形三条高线交于直角顶点;
③钝角三角形的三条高不相交.三条高所在直线交于一点,并且这个点在三角形外部.
锐角三角形 直角三角形 钝角三角形
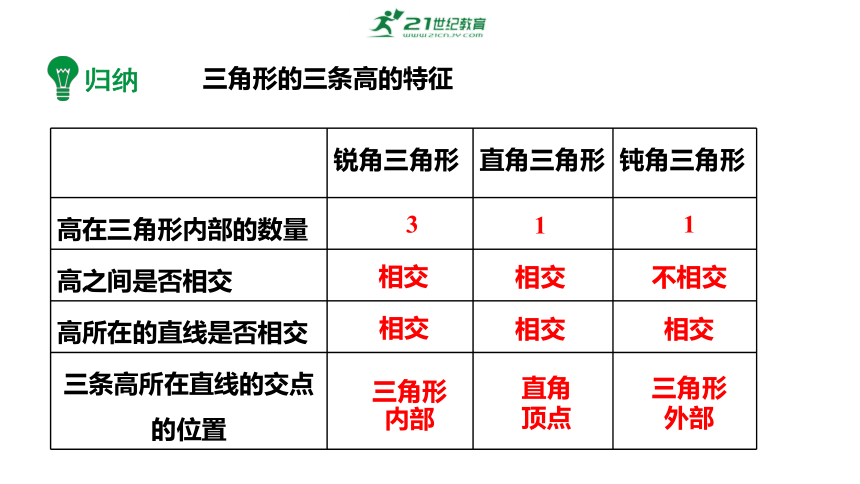
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
三角形的三条高的特征
3
1
1
相交
相交
不相交
相交
相交
相交
三角形
内部
直角顶点
三角形
外部
归纳
例1 如图所示,在△ABC 中,AB=AC=5,BC=6,AD⊥BC 于点 D,且 AD=4,若点 P 在边 AC 上移动,求 BP 的最小值.
解:如图,根据垂线段最短,可知当 BP⊥AC 时,BP 有最小值.
由△ABC 的面积公式可知,
S△ABC= AD · BC= BP · AC.
代入数值,可解得 BP= .
P
1.在下图中,正确画出△ABC 中 BC 边上高的是 ( ).
∟
A
B
C
D
A
B
C
D
∟
A
B
C
D
∟
A
B
C
D
A
B
C
D
C
针对训练
三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫做三角形的角平分线.
角平分线
注意:三角形的角平分线是一条线段.
二 三角形的角平分线
如图,△ABC中,∠1 = ∠2,线段AD就是△ABC的一条角平分线.
画出下列△ABC 的角平分线.
三角形的三条角平分线交于一点(三角形的内心).
操作
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
例2 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB 的度数.
解:因为AD是△ABC的角平分线,∠BAC=60°,
所以∠DAC=∠BAD=30°.
因为CE是△ABC的高,∠BCE=40°,
所以∠B=50°,
所以∠ADB=180°-∠B-∠BAD
=180°-50°-30°=100°.
三 三角形的中线
三角形中,连接一个顶点与它对边中点的线段叫做三角形的中线.
中线
如图,△ABC中,点E是BC的中点,线段AE就是△ABC的一条中线.
操作
画出下列△ABC 的三条边上的中线.
三角形的中线都在三角形内部,且必交于一点.三角形三条中线的交点叫做三角形的重心.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
例3 如图, AD、BE、CF 是△ABC 的三条中线.则
(1) AB = 2___________,BD = _________,CE = _________.
(2) 若 S△ABC = 12,则 S△ABD = _________.
A
B
C
D
F
E
AF(或FB)
CD
AC
6
三角形的任何一条中线把三角形分成
面积相等的两个三角形.
锐角三角形 直角三角形 钝角三角形
角平分线 数量 是否交于一点 中线 数量 是否交于一点 高线 数量 是否交于一点
归纳
三角形的角平分线,中线和高线
3
3
3
相交于三角形内部一点
相交于三角形内部一点
相交于三角形内部一点
相交于直角顶点
三条高不相交,三条高所在直线交于三角形外部一点
(1)“不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形”;
(2)“三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫做三角形的角平分线”;
(3)“整数和分数统称有理数”.
阅读下列语句:
(1)、(2)是三角形、三角形角平分线的定义,(3)是有理数的定义.
四 定义
前两个定义揭示了对象的特征性质,后一个定义明确所指对象的范围.像这样能明确界定某个对象含义的语句叫做定义.
归纳
你还能举出哪些你所熟知的一些定义例子?
举例如下:
1.“具有中华人民共和国国籍的人,叫做中华人民共和国公民” 是“中华人民共和国公民”的定义;
2. “两点之间线段的长度,叫做这两点之间的距离” 是“两点之间的距离”的定义;
3.“在一个方程中,只含有一个未知数,并且未知数的指数是1,这样的方程叫做一元一次方程” 是“一元一次方程”的定义.
1.如图所示,AD是△ABC的中线,已知△ABD的周长为25 cm,AB比AC长6 cm,则△ACD的周长为( )
A.19 cm B.22 cm C.25 cm D.31 cm
分析: △ABD和△ACD周长的差=(AB+BD+AD)–(AC+CD+AD)=AB –AC.
因为△ABD的周长为25 cm,AB比AC长6 cm,
所以△ACD的周长为25–6=19(cm).
A
随堂练习
2. 如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
A
3.如图,在△ABC 中,E 是 BC 上的一点,EC=2BE,点 D 是 AC 的中点,设△ABC,△ADF 和△BEF 的面积分别为 S△ABC,S△ADF 和 S△BEF,且 S△ABC =12,求 S△ADF-S△BEF 的值.
解:因为 点 D 是 AC 的中点, 所以 AD= AC.
因为S△ABC=12,
所以 S△ABD= S△ABC= ×12=6.
因为 S△ABD-S△ABE =(S△ADF+S△ABF)-(S△ABF+S△BEF)
=S△ADF-S△BEF,
所以 S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
因为 EC=2BE,S△ABC=12,
所以 S△ABE= S△ABC= ×12=4.
三角形中几
条重要线段
角平分线
中线
高
三角形中, 连接一 个顶点与它对边中点的线段叫做三
角形的中线
三角形中,一个角的平分 线与这个角对边相交,顶 点与
交点之间的线段叫做 三角形的角平分线
从三角形的一个顶点到它对边所在直线的垂线段叫做
三角形的高线,也叫做 三角形的高
定义
像这样能明确界定某个对象含义的语句叫做定义.
课堂小结
锐角三角形 直角三角形 钝角三角形
角平分线 数量 是否交于一点 中线 数量 是否交于一点 高线 数量 是否交于一点
3
3
3
相交于三角形内部一点
相交于三角形内部一点
相交于三角形内部一点
相交于直角顶点
三条高不相交,三条高所在直线交于三角形外部一点
沪科版
13.1.3 三角形中几条重要线段
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.掌握三角形的高,中线及角平分线的概念及画法.
2.掌握三角形的高,中线及角平分线的简单应用.
3.通过具体实例,了解定义的意义.
学习目标
重点
难点
过三角形的一个顶点,你能画出它的对边的垂线吗
如图,过点P 画直线 AB 的垂线.
P ●
A
B
新课引入
一、三角形的高
从三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线,也叫做三角形的高.
A
B
C
D
注意:标明垂直的记号和垂足的字母.
新知学习
分别画出图中各个三角形三条边上的高.
操作
∟
∟
∟
∟
∟
∟
∟
思考:锐角三角形、直角三角形、钝角三角形中的三条高所在直线的交点各在什么地方
①锐角三角形三条高线都在三角形的内部且交于同一点(三角形的垂心);
②直角三角形三条高线交于直角顶点;
③钝角三角形的三条高不相交.三条高所在直线交于一点,并且这个点在三角形外部.
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在直线的交点的位置
三角形的三条高的特征
3
1
1
相交
相交
不相交
相交
相交
相交
三角形
内部
直角顶点
三角形
外部
归纳
例1 如图所示,在△ABC 中,AB=AC=5,BC=6,AD⊥BC 于点 D,且 AD=4,若点 P 在边 AC 上移动,求 BP 的最小值.
解:如图,根据垂线段最短,可知当 BP⊥AC 时,BP 有最小值.
由△ABC 的面积公式可知,
S△ABC= AD · BC= BP · AC.
代入数值,可解得 BP= .
P
1.在下图中,正确画出△ABC 中 BC 边上高的是 ( ).
∟
A
B
C
D
A
B
C
D
∟
A
B
C
D
∟
A
B
C
D
A
B
C
D
C
针对训练
三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫做三角形的角平分线.
角平分线
注意:三角形的角平分线是一条线段.
二 三角形的角平分线
如图,△ABC中,∠1 = ∠2,线段AD就是△ABC的一条角平分线.
画出下列△ABC 的角平分线.
三角形的三条角平分线交于一点(三角形的内心).
操作
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
例2 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB 的度数.
解:因为AD是△ABC的角平分线,∠BAC=60°,
所以∠DAC=∠BAD=30°.
因为CE是△ABC的高,∠BCE=40°,
所以∠B=50°,
所以∠ADB=180°-∠B-∠BAD
=180°-50°-30°=100°.
三 三角形的中线
三角形中,连接一个顶点与它对边中点的线段叫做三角形的中线.
中线
如图,△ABC中,点E是BC的中点,线段AE就是△ABC的一条中线.
操作
画出下列△ABC 的三条边上的中线.
三角形的中线都在三角形内部,且必交于一点.三角形三条中线的交点叫做三角形的重心.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
例3 如图, AD、BE、CF 是△ABC 的三条中线.则
(1) AB = 2___________,BD = _________,CE = _________.
(2) 若 S△ABC = 12,则 S△ABD = _________.
A
B
C
D
F
E
AF(或FB)
CD
AC
6
三角形的任何一条中线把三角形分成
面积相等的两个三角形.
锐角三角形 直角三角形 钝角三角形
角平分线 数量 是否交于一点 中线 数量 是否交于一点 高线 数量 是否交于一点
归纳
三角形的角平分线,中线和高线
3
3
3
相交于三角形内部一点
相交于三角形内部一点
相交于三角形内部一点
相交于直角顶点
三条高不相交,三条高所在直线交于三角形外部一点
(1)“不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形”;
(2)“三角形中,一个角的平分线与这个角对边相交,顶点与交点之间的线段叫做三角形的角平分线”;
(3)“整数和分数统称有理数”.
阅读下列语句:
(1)、(2)是三角形、三角形角平分线的定义,(3)是有理数的定义.
四 定义
前两个定义揭示了对象的特征性质,后一个定义明确所指对象的范围.像这样能明确界定某个对象含义的语句叫做定义.
归纳
你还能举出哪些你所熟知的一些定义例子?
举例如下:
1.“具有中华人民共和国国籍的人,叫做中华人民共和国公民” 是“中华人民共和国公民”的定义;
2. “两点之间线段的长度,叫做这两点之间的距离” 是“两点之间的距离”的定义;
3.“在一个方程中,只含有一个未知数,并且未知数的指数是1,这样的方程叫做一元一次方程” 是“一元一次方程”的定义.
1.如图所示,AD是△ABC的中线,已知△ABD的周长为25 cm,AB比AC长6 cm,则△ACD的周长为( )
A.19 cm B.22 cm C.25 cm D.31 cm
分析: △ABD和△ACD周长的差=(AB+BD+AD)–(AC+CD+AD)=AB –AC.
因为△ABD的周长为25 cm,AB比AC长6 cm,
所以△ACD的周长为25–6=19(cm).
A
随堂练习
2. 如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75° B.80° C.85° D.90°
A
3.如图,在△ABC 中,E 是 BC 上的一点,EC=2BE,点 D 是 AC 的中点,设△ABC,△ADF 和△BEF 的面积分别为 S△ABC,S△ADF 和 S△BEF,且 S△ABC =12,求 S△ADF-S△BEF 的值.
解:因为 点 D 是 AC 的中点, 所以 AD= AC.
因为S△ABC=12,
所以 S△ABD= S△ABC= ×12=6.
因为 S△ABD-S△ABE =(S△ADF+S△ABF)-(S△ABF+S△BEF)
=S△ADF-S△BEF,
所以 S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
因为 EC=2BE,S△ABC=12,
所以 S△ABE= S△ABC= ×12=4.
三角形中几
条重要线段
角平分线
中线
高
三角形中, 连接一 个顶点与它对边中点的线段叫做三
角形的中线
三角形中,一个角的平分 线与这个角对边相交,顶 点与
交点之间的线段叫做 三角形的角平分线
从三角形的一个顶点到它对边所在直线的垂线段叫做
三角形的高线,也叫做 三角形的高
定义
像这样能明确界定某个对象含义的语句叫做定义.
课堂小结
锐角三角形 直角三角形 钝角三角形
角平分线 数量 是否交于一点 中线 数量 是否交于一点 高线 数量 是否交于一点
3
3
3
相交于三角形内部一点
相交于三角形内部一点
相交于三角形内部一点
相交于直角顶点
三条高不相交,三条高所在直线交于三角形外部一点
