13.2 命题与证明第1课时命题课件课件(共22张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 13.2 命题与证明第1课时命题课件课件(共22张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 838.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 11:49:38 | ||
图片预览








文档简介
(共22张PPT)
沪科版
13.2.1 命题
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.通过具体实例,了解命题的意义.
2.通过具体实例,会区分命题的条件和结论,了解原命题及其逆命题的概念.会识别两个互逆的命题,知道原命题成立其逆命题不一定成立.
3.了解反例的作用,知道利用反例可以判断一个命题是错误的.
学习目标
重点
重点
难点
我们已经学习了一些几何图形的性质.在认识这些性质时,使用了观察、操作和实验等方法,并对它们作出一些说理与解释.
研究几何图形,如果仅限于观察、操作和实验等方法,难以使人确信结果的正确性,比如上一节研究三角形性质时,通过折叠、剪拼或度量得到三角形三个内角的和是180°(图中是剪拼).
新课引入
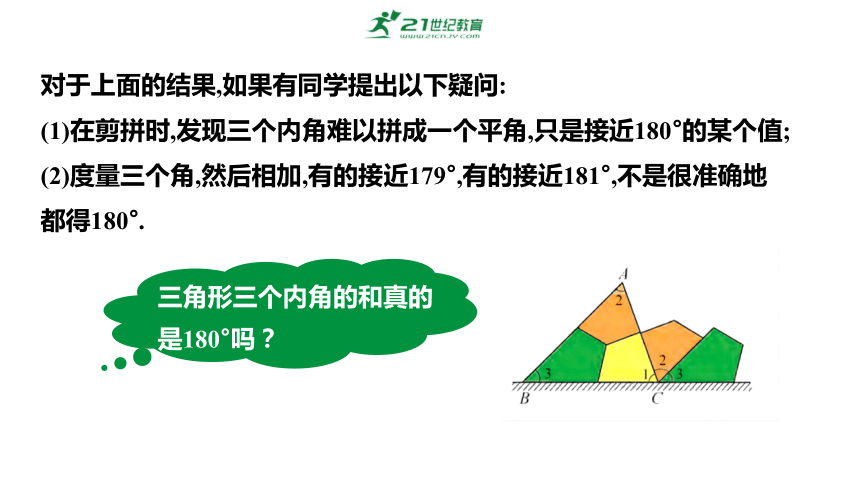
对于上面的结果,如果有同学提出以下疑问:
(1)在剪拼时,发现三个内角难以拼成一个平角,只是接近180°的某个值;
(2)度量三个角,然后相加,有的接近179°,有的接近181°,不是很准确地都得180°.
三角形三个内角的和真的是180°吗?
学习几何需要观察和实验,同时也需要学会推理.从这一章起我们将系统学习用逻辑推理方法对几何中的结论进行论证.
如何回答上面的问题呢
推理是一种思维活动.人们在思维活动中,常要对事物的情况作出种种判断.判断是通过语言来表达的.
(1)北京是中华人民共和国的首都; ( )
(2)如果∠1与∠2是对顶角,那么∠1=∠2; ( )
一 命题
思考
以下判断哪些是正确的?哪些是错误的?
新知学习
从上面各语句中可以看出,人们对于客观事物情况的判断可能是正确的,也可能是错误的.上述语句(1)(2)(4)是正确的判断,(3)是错误的判断.
(3)1 +1 <2; ( )
(4)如果一个整数的各位上的数字之和是3的倍数,那么这个数能被3整除.
( )
像这样,对某一事件作出正确或不正确判断的语句(或式子)叫做命题.上面判断性语句(1)(2)(4)都是正确的命题,我们称之为真命题;
(3)是错误的命题,我们称之为假命题.
归纳
(1)你的作业做完了吗
(2)欢迎前来参观!
(3)以点О为圆心,3 cm长为半径画弧.
如果一个语句没有对某一事件的正确与否作出任何判断,那么它就不是命题.
像这样对某一事件的正确与否没有给出任何判断就不是命题.
因此,祈使句、疑问句、感叹句都不是命题.
观察下列命题,你能发现这些命题有什么共同的特征?
(1)如果两个三角形的三条边分别相等,那么这两个三角形的周长相等;
(2)如果两个数的绝对值相等,那么这两个数也相等;
(3)如果一个数的平方等于9,那么这个数是3.
数学命题通常由题设和结论两部分组成,命题常写成“如果……
那么……”的形式.
思考
以“如果……那么……”为关联词的命题的一般形式是“如果p ,那么q” ,或者说成“若p,则q”,其中p是这个命题的条件(或题设),q是这个命题的结论(或题断).
有时为了叙述简便,也可以省略关联词“如果”“那么”.
如命题“如果两个角是对顶角,那么这两个角相等”可以写成“对顶角相等”.
例1 指出下列命题的条件与结论:
(1)两条直线都平行于同一条直线,这两条直线平行;
(2)如果∠A = ∠B,那么∠A 的补角与∠B的补角相等.
解:(1)“两条直线都平行于同一条直线”是条件,“两条直线平行”是结论.
(2)“∠A = ∠B”是条件,“∠A 的补角与∠B的补角相等”是结论.
例2 把下列命题改写成“如果p,那么q”的形式,并指出它们的条件和结论.
(1)平行于同一条直线的两直线平行;
(2)两直线相交,只有一个交点.
(1)如果两条直线平行于同一条直线,那么这两条直线平行.
其中“两条直线平行于同一条直线”是条件,“这两条直线平行”是结论.
(2)如果两条直线相交,那么它们只有一个交点.
其中“两条直线相交”是条件,“它们只有一个交点”是结论.
将命题“如果p ,那么q”中的条件与结论互换,便得到一个新命题“如果q,那么p”,我们把这样的两个命题称为互逆命题.
其中一个叫做原命题;
另一个就叫做原命题的逆命题.
二 互逆命题与举反例
如果原命题是真命题,那么它的逆命题也是真命题吗?
例如“如果∠1与∠2是对顶角,那么∠1 =∠2”是真命题,
但它的逆命题“如果∠1=∠2,那么∠1与∠2是对顶角”却是假命题.
当一个命题是真命题时,它的逆命题不一定是真命题.
1
2
1
2
怎样说明这个命题是假的呢?只要举出一个例子即可.
如图,画出一个角的平分线后,可得∠1 =∠2,显然,这里∠1与∠2不是对顶角.
像这种符合命题条件,但不满足命题结论的例子,我们称之为反例.
要说明一个命题是假命题,只要举出一个反例即可.
归纳
例3 写出下列命题的逆命题,并判断所得逆命题的真假,如果是假命题,请举一个反例:
(1)内错角相等,两直线平行;
(2)如果a =0,那么ab =0.
解:(1)逆命题是“两直线平行,内错角相等”,是真命题
(2)逆命题是“如果ab =0,那么a=0”,是假命题.
反例,当a =1 , b =0时,ab =0.
1.下列命题中,是真命题的是( )
A.若a⊥b,b⊥c,则a⊥c
B.在平面直角坐标系内,点P(-2,3)到x轴的距离等于2
C.无限小数都是无理数
D.经过直线外一点,有且只有一条直线与这条直线平行
D
随堂练习
2.在命题“同位角相等,两直线平行”中,条件是________________,结论是________________;它的逆命题是:__________________________,该逆命题是_____(“真”/“假”)命题.
同位角相等
两直线平行
两直线平行,同位角相等
真
3.举反例说明下列命题是假命题.
(1)若两个角不是对顶角,则这两个角不相等;
(2)若ab=0,则a+b=0.
(3) 大于 90° 的角是钝角;
解:(1)两条直线平行形成的内错角,这两个角不是对顶角,但是它们相等;
(2)当a=5,b=0时,ab=0,但a+b≠0.
(3) 180° 的角大于 90°,但 180° 不是钝角,而是平角.
命题
定义
组成
分类
若p,则q”,其中p是这个命题的条件(或题设),
q是这个命题的结论(或题断).
对某一事件作出正确或不正确判断的语句
正确的命题叫做真命题;
错误的命题叫做假命题.
互逆命题
将命题的条件与结论互换,便得到一个新命题,这样
的两个命题称为互逆命题.其中一个叫做原命题;
另一个就叫做原命题的逆命题.
课堂小结
沪科版
13.2.1 命题
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1.通过具体实例,了解命题的意义.
2.通过具体实例,会区分命题的条件和结论,了解原命题及其逆命题的概念.会识别两个互逆的命题,知道原命题成立其逆命题不一定成立.
3.了解反例的作用,知道利用反例可以判断一个命题是错误的.
学习目标
重点
重点
难点
我们已经学习了一些几何图形的性质.在认识这些性质时,使用了观察、操作和实验等方法,并对它们作出一些说理与解释.
研究几何图形,如果仅限于观察、操作和实验等方法,难以使人确信结果的正确性,比如上一节研究三角形性质时,通过折叠、剪拼或度量得到三角形三个内角的和是180°(图中是剪拼).
新课引入
对于上面的结果,如果有同学提出以下疑问:
(1)在剪拼时,发现三个内角难以拼成一个平角,只是接近180°的某个值;
(2)度量三个角,然后相加,有的接近179°,有的接近181°,不是很准确地都得180°.
三角形三个内角的和真的是180°吗?
学习几何需要观察和实验,同时也需要学会推理.从这一章起我们将系统学习用逻辑推理方法对几何中的结论进行论证.
如何回答上面的问题呢
推理是一种思维活动.人们在思维活动中,常要对事物的情况作出种种判断.判断是通过语言来表达的.
(1)北京是中华人民共和国的首都; ( )
(2)如果∠1与∠2是对顶角,那么∠1=∠2; ( )
一 命题
思考
以下判断哪些是正确的?哪些是错误的?
新知学习
从上面各语句中可以看出,人们对于客观事物情况的判断可能是正确的,也可能是错误的.上述语句(1)(2)(4)是正确的判断,(3)是错误的判断.
(3)1 +1 <2; ( )
(4)如果一个整数的各位上的数字之和是3的倍数,那么这个数能被3整除.
( )
像这样,对某一事件作出正确或不正确判断的语句(或式子)叫做命题.上面判断性语句(1)(2)(4)都是正确的命题,我们称之为真命题;
(3)是错误的命题,我们称之为假命题.
归纳
(1)你的作业做完了吗
(2)欢迎前来参观!
(3)以点О为圆心,3 cm长为半径画弧.
如果一个语句没有对某一事件的正确与否作出任何判断,那么它就不是命题.
像这样对某一事件的正确与否没有给出任何判断就不是命题.
因此,祈使句、疑问句、感叹句都不是命题.
观察下列命题,你能发现这些命题有什么共同的特征?
(1)如果两个三角形的三条边分别相等,那么这两个三角形的周长相等;
(2)如果两个数的绝对值相等,那么这两个数也相等;
(3)如果一个数的平方等于9,那么这个数是3.
数学命题通常由题设和结论两部分组成,命题常写成“如果……
那么……”的形式.
思考
以“如果……那么……”为关联词的命题的一般形式是“如果p ,那么q” ,或者说成“若p,则q”,其中p是这个命题的条件(或题设),q是这个命题的结论(或题断).
有时为了叙述简便,也可以省略关联词“如果”“那么”.
如命题“如果两个角是对顶角,那么这两个角相等”可以写成“对顶角相等”.
例1 指出下列命题的条件与结论:
(1)两条直线都平行于同一条直线,这两条直线平行;
(2)如果∠A = ∠B,那么∠A 的补角与∠B的补角相等.
解:(1)“两条直线都平行于同一条直线”是条件,“两条直线平行”是结论.
(2)“∠A = ∠B”是条件,“∠A 的补角与∠B的补角相等”是结论.
例2 把下列命题改写成“如果p,那么q”的形式,并指出它们的条件和结论.
(1)平行于同一条直线的两直线平行;
(2)两直线相交,只有一个交点.
(1)如果两条直线平行于同一条直线,那么这两条直线平行.
其中“两条直线平行于同一条直线”是条件,“这两条直线平行”是结论.
(2)如果两条直线相交,那么它们只有一个交点.
其中“两条直线相交”是条件,“它们只有一个交点”是结论.
将命题“如果p ,那么q”中的条件与结论互换,便得到一个新命题“如果q,那么p”,我们把这样的两个命题称为互逆命题.
其中一个叫做原命题;
另一个就叫做原命题的逆命题.
二 互逆命题与举反例
如果原命题是真命题,那么它的逆命题也是真命题吗?
例如“如果∠1与∠2是对顶角,那么∠1 =∠2”是真命题,
但它的逆命题“如果∠1=∠2,那么∠1与∠2是对顶角”却是假命题.
当一个命题是真命题时,它的逆命题不一定是真命题.
1
2
1
2
怎样说明这个命题是假的呢?只要举出一个例子即可.
如图,画出一个角的平分线后,可得∠1 =∠2,显然,这里∠1与∠2不是对顶角.
像这种符合命题条件,但不满足命题结论的例子,我们称之为反例.
要说明一个命题是假命题,只要举出一个反例即可.
归纳
例3 写出下列命题的逆命题,并判断所得逆命题的真假,如果是假命题,请举一个反例:
(1)内错角相等,两直线平行;
(2)如果a =0,那么ab =0.
解:(1)逆命题是“两直线平行,内错角相等”,是真命题
(2)逆命题是“如果ab =0,那么a=0”,是假命题.
反例,当a =1 , b =0时,ab =0.
1.下列命题中,是真命题的是( )
A.若a⊥b,b⊥c,则a⊥c
B.在平面直角坐标系内,点P(-2,3)到x轴的距离等于2
C.无限小数都是无理数
D.经过直线外一点,有且只有一条直线与这条直线平行
D
随堂练习
2.在命题“同位角相等,两直线平行”中,条件是________________,结论是________________;它的逆命题是:__________________________,该逆命题是_____(“真”/“假”)命题.
同位角相等
两直线平行
两直线平行,同位角相等
真
3.举反例说明下列命题是假命题.
(1)若两个角不是对顶角,则这两个角不相等;
(2)若ab=0,则a+b=0.
(3) 大于 90° 的角是钝角;
解:(1)两条直线平行形成的内错角,这两个角不是对顶角,但是它们相等;
(2)当a=5,b=0时,ab=0,但a+b≠0.
(3) 180° 的角大于 90°,但 180° 不是钝角,而是平角.
命题
定义
组成
分类
若p,则q”,其中p是这个命题的条件(或题设),
q是这个命题的结论(或题断).
对某一事件作出正确或不正确判断的语句
正确的命题叫做真命题;
错误的命题叫做假命题.
互逆命题
将命题的条件与结论互换,便得到一个新命题,这样
的两个命题称为互逆命题.其中一个叫做原命题;
另一个就叫做原命题的逆命题.
课堂小结
