14.2三角形全等的判定第3课时三边分别相等的两个三角形课件(共17张PPT)2024-2025学年度八年级上册沪科版数学
文档属性
| 名称 | 14.2三角形全等的判定第3课时三边分别相等的两个三角形课件(共17张PPT)2024-2025学年度八年级上册沪科版数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-09-04 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
沪科版
14.2.3 三边分别相等
的两个三角形
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 掌握基本事实:三边分别相等的两个三角形全等.
2.了解三角形的稳定性,并会运用三角形的稳定性去解决实际问题.
学习目标
重点
以三根小木棍的长为边长搭三角形,你能搭出几种呢?试试看.
只能搭出唯一的三角形.
新课引入
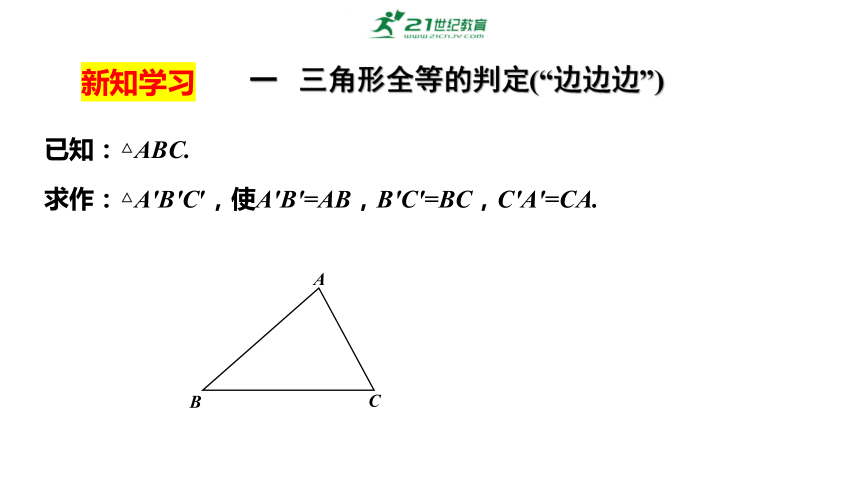
已知:△ABC.
求作:△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA.
一 三角形全等的判定(“边边边”)
A
C
B
新知学习
A
C
B
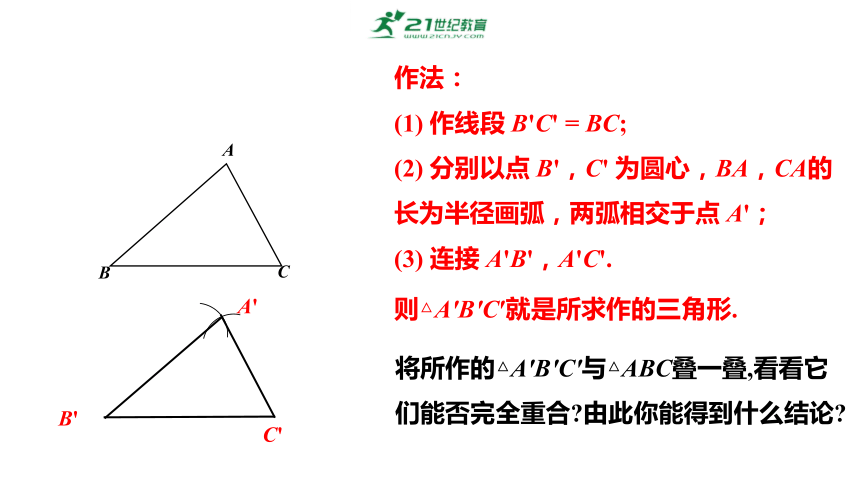
作法:
(1) 作线段 B'C' = BC;
(2) 分别以点 B',C' 为圆心,BA,CA的 长为半径画弧,两弧相交于点 A';
(3) 连接 A'B',A'C'.
B'
C'
A'
则△A′B′C′就是所求作的三角形.
将所作的△A'B'C'与△ABC叠一叠,看看它们能否完全重合 由此你能得到什么结论
现象:两个三角形能完全重合.
说明:这两个三角形全等.
三边分别相等的两个三角形全等. 简记为“边边边”或“SSS”.
判定两个三角形全等的第3种方法是如下的基本事实.
归纳
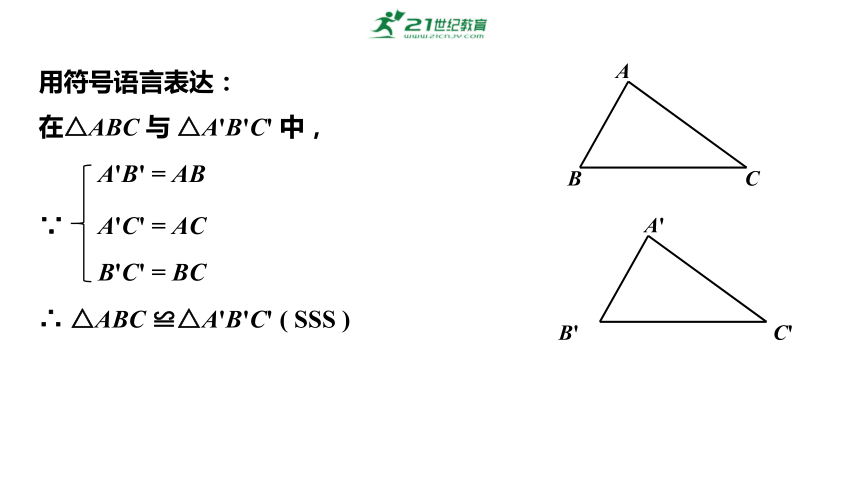
用符号语言表达:
在△ABC 与 △A'B'C' 中,
∵
B'C' = BC
A'C' = AC
A'B' = AB
∴ △ABC ≌△A'B'C' ( SSS )
A
B
C
A'
B'
C'
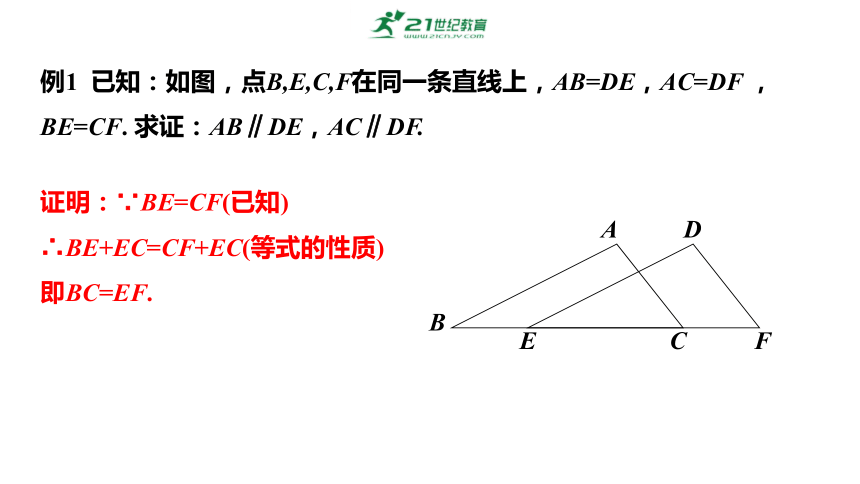
例1 已知:如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF ,BE=CF. 求证:AB∥DE,AC∥DF.
A
B
E
C
F
D
证明:∵BE=CF(已知)
∴BE+EC=CF+EC(等式的性质)
即BC=EF.
在△ABC和△DEF中,
∵
AB=DE(已知)
AC=DF (已知)
BC=EF (已证)
∴△ABC≌△DEF(SSS)
∴∠B=∠DEF,∠ACB=∠F(全等三角形的对应角相等)
∴AB//DE,AC//DF.(同位角相等,两直线平行)
A
B
E
C
F
D
例2 如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
H
D
C
B
A
解:有三组
△ABH≌△ACH(SSS);
△ABD≌△ACD(SSS);
△DBH≌△DCH(SSS).
上面的结论说明,只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定,这个性质叫做三角形的稳定性.
你能举例说出生活中三角形稳定性的例子吗?
二 三角形的稳定性
如斜拉桥上的三角形结构、自行车的三角形车架;又如在预制的木门框(或木窗框)上加两根木条[图(1)]、晃动了的椅子腿与坐板间钉一根木条[图(2)]构成三角形,以防门框变形、椅子摇晃.
A. 两点之间线段最短
B. 三角形两边之和大于第三边
C. 长方形的四个角都是直角
D. 三角形的稳定性
D
例3 如图,工人师傅砌门时,常用木条 EF 固定矩形门框,使其不变形,这种做法的根据是( )
1.如图,同学们平时所骑的自行车,中间的主体部分一般是三角形形状,这样一方面是为了美观,另一方面是出于安全考虑,这样做是因为________________________.
三角形具有稳定性
随堂练习
2.如图,有一个三角形钢架,AB = AC,AD 是连接点 A 与 BC 中点 D 的支架,求证:△ABD≌△ACD.
A
D
C
B
分析:要证△ABD≌△ACD,只需看这两个三角形的三条边是否分别相等.
证明: ∵D 是 BC 的中点,
∴BD = DC.
在△ABD 与△ACD 中
AB = AC
∵ BD = CD
AD = AD
∴△ABD≌△ACD (SSS) .
A
D
C
B
证明:∵AD=BC,∴AC=BD,
在△ACE和△BDF中,
∴△ACE≌△BDF.(SSS)
∴∠A=∠B.
∴AE∥BF.
3.已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:AE∥BF.
三角形的
稳定性
三边分别相等的两个三角形全等.简记为“边边边”或“SSS”.
只要三角形三边的长度确定了,这个三角形的形状和大
小就完全确定,这个性质叫做三角形的稳定性.
三边分别相等
的两个三角形
基本事实
课堂小结
沪科版
14.2.3 三边分别相等
的两个三角形
八年级上
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
目录
1. 掌握基本事实:三边分别相等的两个三角形全等.
2.了解三角形的稳定性,并会运用三角形的稳定性去解决实际问题.
学习目标
重点
以三根小木棍的长为边长搭三角形,你能搭出几种呢?试试看.
只能搭出唯一的三角形.
新课引入
已知:△ABC.
求作:△A′B′C′,使A′B′=AB,B′C′=BC,C′A′=CA.
一 三角形全等的判定(“边边边”)
A
C
B
新知学习
A
C
B
作法:
(1) 作线段 B'C' = BC;
(2) 分别以点 B',C' 为圆心,BA,CA的 长为半径画弧,两弧相交于点 A';
(3) 连接 A'B',A'C'.
B'
C'
A'
则△A′B′C′就是所求作的三角形.
将所作的△A'B'C'与△ABC叠一叠,看看它们能否完全重合 由此你能得到什么结论
现象:两个三角形能完全重合.
说明:这两个三角形全等.
三边分别相等的两个三角形全等. 简记为“边边边”或“SSS”.
判定两个三角形全等的第3种方法是如下的基本事实.
归纳
用符号语言表达:
在△ABC 与 △A'B'C' 中,
∵
B'C' = BC
A'C' = AC
A'B' = AB
∴ △ABC ≌△A'B'C' ( SSS )
A
B
C
A'
B'
C'
例1 已知:如图,点B,E,C,F在同一条直线上,AB=DE,AC=DF ,BE=CF. 求证:AB∥DE,AC∥DF.
A
B
E
C
F
D
证明:∵BE=CF(已知)
∴BE+EC=CF+EC(等式的性质)
即BC=EF.
在△ABC和△DEF中,
∵
AB=DE(已知)
AC=DF (已知)
BC=EF (已证)
∴△ABC≌△DEF(SSS)
∴∠B=∠DEF,∠ACB=∠F(全等三角形的对应角相等)
∴AB//DE,AC//DF.(同位角相等,两直线平行)
A
B
E
C
F
D
例2 如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
H
D
C
B
A
解:有三组
△ABH≌△ACH(SSS);
△ABD≌△ACD(SSS);
△DBH≌△DCH(SSS).
上面的结论说明,只要三角形三边的长度确定了,这个三角形的形状和大小就完全确定,这个性质叫做三角形的稳定性.
你能举例说出生活中三角形稳定性的例子吗?
二 三角形的稳定性
如斜拉桥上的三角形结构、自行车的三角形车架;又如在预制的木门框(或木窗框)上加两根木条[图(1)]、晃动了的椅子腿与坐板间钉一根木条[图(2)]构成三角形,以防门框变形、椅子摇晃.
A. 两点之间线段最短
B. 三角形两边之和大于第三边
C. 长方形的四个角都是直角
D. 三角形的稳定性
D
例3 如图,工人师傅砌门时,常用木条 EF 固定矩形门框,使其不变形,这种做法的根据是( )
1.如图,同学们平时所骑的自行车,中间的主体部分一般是三角形形状,这样一方面是为了美观,另一方面是出于安全考虑,这样做是因为________________________.
三角形具有稳定性
随堂练习
2.如图,有一个三角形钢架,AB = AC,AD 是连接点 A 与 BC 中点 D 的支架,求证:△ABD≌△ACD.
A
D
C
B
分析:要证△ABD≌△ACD,只需看这两个三角形的三条边是否分别相等.
证明: ∵D 是 BC 的中点,
∴BD = DC.
在△ABD 与△ACD 中
AB = AC
∵ BD = CD
AD = AD
∴△ABD≌△ACD (SSS) .
A
D
C
B
证明:∵AD=BC,∴AC=BD,
在△ACE和△BDF中,
∴△ACE≌△BDF.(SSS)
∴∠A=∠B.
∴AE∥BF.
3.已知:如图,点A,D,C,B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:AE∥BF.
三角形的
稳定性
三边分别相等的两个三角形全等.简记为“边边边”或“SSS”.
只要三角形三边的长度确定了,这个三角形的形状和大
小就完全确定,这个性质叫做三角形的稳定性.
三边分别相等
的两个三角形
基本事实
课堂小结
